2. EXPERIMENTS AND NUMERICAL SIMULATIONS

The experiments were performed in a shock tube as described by Erez et al. (2000). The bubble was created with a thin soap membrane and then inflated using a special needle. This needle was then used to suspend it from the upper side of the tube until the impact of the shock wave. The needle does not affect the large-scale flow of the bubble. Helium (η = 0.138) was used for the slow/fast interaction and SF₆ (η = 5.034) for the fast/slow interactions. The shock wave strength was Mach = 1.22 and Mach = 1.17, respectively.

The simulations are done using Leeor2D, a full two-dimensional (2D) interface-tracing ALE hydrodynamic code. The geometry of the simulations is set according to the experiment with one difference; the simulations are axis symmetric and so have a circular cross section in contrast to the square cross section of the experimental shock tube. This difference and any three-dimensional (3D) effects have little influence on the morphology of the interaction as can be seen from the comparison of the simulations and experiments. This is done in Figure 1, where the 2D interface of the bubble is superimposed on the experiment Schlieren photographs and it shows a good agreement between them.

Slow/fast (He bubble) and fast/slow (SF6) experiments on which the simulation 2D interfaces are superimposed. The timing of the images are (a) t = 0.064 ms, (b) t = 0.264 ms, (c) t = 0.364 ms, (d) t = 0.564 ms for the slow/fast case and (a′) t = 0.042 ms, (b′) t = 0.242 ms, (c′) t = 0.442 ms, (d′) t = 0.642 ms for the fast/slow case.

3. DIMENSIONAL ANALYSIS

The interaction can be characterized using the following five parameters: the bubble radius R, speed of sound in the surrounding air c_s, Mach number M, density ratio η, and the ratio of specific heats γ (taken as the ratio for the two gases). Out of the five parameters, only the first two possess physical units while the other three are dimensionless. In this section, the scaling of the circulation and velocity will be derived based on dimensional analysis using these two parameters. It should be noted that the parameters can be normalized and defined differently but that will not alter the scaling.

The vorticity maps from the simulations show that the flow is rotational and that the vorticity is baroclinicly generated by the shock wave. The net amount of vorticity in a given area is defined as the circulation Γ = ∮·dl = ∫ω·dA, where ω = ∇ × v is the vorticity and v is the velocity. In isentropic flow, the circulation in a given contour is conserved. In VDM the circulation for the fast/slow case is derived (assuming that γ is identical for both gases):

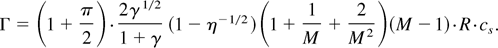
The dimensions of circulation are [Γ] = [length]²/[time]. Hence, from dimensional analysis, the circulation must have the form of Γ = f (M, γ, η)·R·c_s, where f is an arbitrary function of the three dimensionless parameters η, γ, and M.

The velocity field is a function of the circulation, and so the latter has to be incorporated in its dimensional analysis. The velocity dimensions are [U] = [length]/[time], leading to the following relationship between the velocity and circulation:

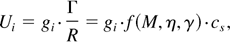
where g_i is a constant representing the influence of the topology of the problem. The index i refers to the specific velocity, for example, ring velocity or the jet velocity, and so the above expression is general and is applicable to any of the velocities that can be defined. The main conclusion is that the velocity field is independent of the bubble radius and that scaling of the velocities is invariant to the definition of the velocity (the only difference will be the value of the constant).

For example, Saffman (1970) showed that the velocity of an ideal inviscid vortex ring is

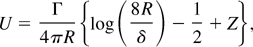
where δ is the radius of a circular core, R is the radius of the vortex ring, and Z is an integral of the circulation in the vortex core. The ratio Γ/R has the dimensions of speed and the ratio R/δ is dimensionless. This indicates that the velocity is practically radius independent.

4. TYPICAL SIMULATION

The evolution of a typical simulation of the slow/fast and fast/slow interaction is displayed in Figure 2. Zabusky and Zeng (1998) applied the VDM to the fast/slow interaction. This study will treat the slow/fast case only and in the future the investigation will be continued to the fast/slow interaction. The density maps show that the density of the bubble is uniform and constant in comparison to the density of the ambient air, so that the interaction is incompressible. The vorticity distribution is not uniform and is concentrated on the surface of the bubble until the vortex ring is formed. In the fast/slow interaction, the vortex ring is very sensitive to the resolution and is harder to simulate.

Density (gr/cm3) (upper half) and normalized vorticity (lower half) maps of the slow/fast (He bubble) and fast/slow (SF6) simulations. The images are timed according to the results in Figure 1.

In stage (a) the transmitted shock wave (TS) has emerged from the bubble, which is still intact. The vorticity is concentrated on the surface of the bubble, especially on the upstream side. In stage (b), the upstream side of the bubble intersects (IS) the downstream side. The motion of the upstream side causes a shear velocity resulting in a concentration of vorticity on the inner side of the bubble. The vortex ring (VR) is visible at stage (c) and from this point onwards the vorticity is concentrated in the ring. The velocity of the ring is higher than that of the large upstream remains, and in stage (d) they are almost completely separate.

5. VORTEX RING VELOCITY

An examination of the longitudinal velocity distribution along the symmetry axis enables us to characterize the motion of the vortex ring. Figure 3 is the space–time velocity map. The position of the shock wave can be easily identified. The prominent feature is the region of high velocity behind the shock wave. This region is moving downstream with a constant velocity. The velocity distribution in this region is symmetric with the maximum velocity located at the position of the vortex ring on the axis. This can be expected because of the rotational nature of the flow; air is drawn into the ring and, at the center, has only a velocity component in the direction of the symmetry axis. After the air passes through the center, it begins to move to the sides as well. The position of the vortex ring can therefore be distinguished by the position of the maximum velocity. For the simulation in Figure 3, the vortex ring velocity is calculated as 176 m/s in good comparison with the experimental value of 164 ± 19 m/s (calculated from the experiment pictures).

Space–time map of the symmetry axis longitudinal velocity (cm/s), insert—velocity profile at t = 0.4 ms.

The dimensional analysis is performed for an arbitrary velocity, leading to the conclusion that the dependence on the parameters is identical for different velocities. Hence the ratio of two velocities is independent of the parameters and is equal to the ratio of the constant g_i. For example, the ratio of the ring velocity and the maximum velocity: V_max /V_ring = g_max /g_ring was computed as a function of the Mach number. The maximum deviation from the average is 4.5%, which is small compared to the variation in the Mach number from 1.22 to 4.

6. RADIUS SCALING

In Section 3, it was claimed that the velocity is independent of the initial radius of the bubble. This assertion was investigated by executing simulations with different bubble radii. The radii used are 0.2, 1, and 5 cm, that is, a factor of 5 between each simulation. The simulation results are superimposed on each other in Figure 4. The time and the position axis are normalized by the initial bubble radius:

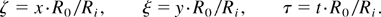
Interfaces of simulations with radii: 0.2, 1, and 5 cm superimposed.

There is a very good agreement in the position and shape of the bubbles. Quantifiably, the normalized ring velocities are 3278, 3297, and 3296, respectively, a deviation of less than 1%. This supports the claim that the velocity is radius independent.

7. MACH SCALING

In the equation derived for the ring velocity there is an arbitrary dimensionless function of the Mach number, density ratio, and specific heat ratio. Assuming that the variables are separable, the dependence of the velocity on the Mach number can be investigated. The Mach scaling is obtained from the scaling of the circulation derived in the VDM. This value was calculated and compared to the circulation computed for the typical simulation with a deviation of less than 5%. The constant representing the other variables was determined from the ring velocity for the M = 1.22 simulation.

The graph of the ring velocity as a function of the Mach number is plotted in Figure 5. There is a comparison of the velocities from the simulations and those calculated using the scaling. There is a good agreement for Mach numbers lower than M = 2, above which a significant difference increases with the Mach number. In addition, there is a change in the shape of the curve. The curve has a linear asymptotic behavior. This can be predicted from the proposed scaling factor.

Mach number scaling of the velocity (cm/s); comparison between simulation (dotted line) and VDM scaling (solid line).

This change is explained by what can be defined as a competition between the incident shock wave and the upstream interface of the bubble. The competition is illustrated in Figure 6 by the pressure contours of three different simulations at two different times. The three simulations are shown at the same physical time. The time is normalized by the Mach number. In the first time, the transverse shock wave is still located in the bubble, and in the second, the shock wave has already emerged from the bubble.

Upstream interface/shock wave competition, pressure maps for simulations with (a) M = 1.5, (b) M = 2, and (c) M = 3 at the same physical time of t·M = 0.281 ms.

The origin of this change is in the derivation of the scaling factor in the model of Samtaney and Zabusky (1994). The model assumes that the deposition of vorticity is performed by the passage of a shock wave over a completely spherical bubble. This is the case for the simulation of Mach = 1.5 as it passes over the downstream undisturbed side of the bubble. However, it can be seen that for the higher Mach numbers, the upstream interface moves faster than the shock wave. Consequently, the intersection of the upstream and downstream sides of the bubble occurs before the shock wave completes its transition along the entire surface of the bubble. Therefore, the morphology of the interaction is different, because the shock wave now encounters a disturbed surface. The derivation of the scaling factor for the higher Mach numbers is not completely valid and has to be modified. As it turns out, a modification should allow for a higher velocity than previously predicted.

An important point that should be noted is that at around Mach = 1.8, the velocity of the shocked air in a nonmoving coordinate system is greater than the speed of sound for air (∼340 m/s). This means that no information can travel faster than the air penetrating the bubble. The result is breakup of the downstream bubble interface by the penetrating air. This explanation is analogous to the classification performed by Ray et al. (2000), where the interaction is between shock waves and heavy gaseous elliptic cylinders. The flow was divided into two different modes, each describing different interactions of the incident shock and transmitted shock on the leeward side of the ellipse. The application of the VDM was adjusted for the different morphology in each mode.

8. SUMMARY

The phenomenon of a shock wave–bubble interaction was investigated using shock tube experiments and full 2D hydrodynamic simulations. This is performed for both the slow/fast and fast/slow interactions. The position and shape of the bubble was compared and good agreement was achieved.

The basic approach to the interaction was to use dimensional analysis to formulate a scaling equation for the velocity field. This approach is a straightforward one that is based on the relationship between the flow variables and the flow parameters with dimensions. In this interaction, the focus is on the dependence of the velocity on the initial bubble radius and the Mach number. The Mach scaling was obtained from the vorticity deposition model of Samtaney and Zabusky (1994). The velocity is shown to be independent of the radius.

The analysis is performed for the slow/fast interaction (helium bubble in air). Scaling is found to be valid for Mach numbers below 2, whereas for Mach > 2 the simulation value is higher than the value predicted by the scaling. This was explained by introducing the competition between the incident shock wave and the upstream interface of the bubble. This competition determines the morphology of the interaction and the validity of the scaling factor.