2. THIRD HARMONIC CURRENT DENSITY

Consider a clustered gas jet of argon which is formed by adiabatic expansion and hence cooling of gas into a vacuum. Backing pressure, temperature, geometry of nozzle, and other factors are adjusted in such a way that this structured nozzle produces clusters of radius r and space periodic density ${n_{\rm c}} = n_{{\rm c0}}^{0} + n_{\rm c}^{0} {\rm exp}$$(\iota {k_{0}}z)$. Here $n_{{\rm c0}}^{0} $ is initial cluster density and $n_{\rm c}^{0} $ is initial ripple density of cluster. Such density ripple in plasma and cluster can be produced by using a machining laser (Pai et al., Reference Pai, Huang, Kuo, Lin, Wang, Chen, Lee and LINs2005; Liu & Tripathi, Reference Liu and Tripathi2008) or circular grating axicon assembly to generate hydrogen and argon plasma waveguides in a cryogenic cluster jet in a space periodic manner (Layer et al., Reference Layer, York, Antonsen, Varma, Chen, Leng and Milchberg2007). Wave vector ${\vec k_{0}}$ of density ripple is considered to be parallel to z-axis. The free electron density inside cluster is n _e, while outside cluster due to intensity dependent ionization rate it varies sinusoidally as ${n_{0}} = n_{{\rm 00}}^{0} + n_{0}^{0} {\rm exp}(\iota {k_{0}}z)$, where $n_{{\rm 00}}^{0} $ is the initial plasma electron density and $n_{0}^{0} $ is the initial ripple density of plasma electrons. Such type of sinusoidal plasma density ripple has already been used by Xia (Reference Xia2014) with cosine component only. A laser beam of frequency ω₁ and wave number k ₁ propagates through clustered plasma. The electric and magnetic field of laser beam are given by

(1)$${\vec E}_1 = {\hat x}A_1(z,t)e^{-i({\rm \omega}_{1} t - k_{1}z)},$$

(2)$${\vec B_1} = c{\vec k}_1 \times {\vec E}_1/{{\rm \omega} _1},$$

where A ₁(z, t) = F(z − v _g1t) is amplitude of electric field vector and A ₁|_z=0 = A ₀, c is the speed of light in vacuum. The wave number k ₁ and group velocity v _g1 of the laser beam can be expressed as,

(3)$${k_1} = \displaystyle{{{{\rm \omega} _1}} \over c}{\left[ {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _1^2}} - \displaystyle{{4{\rm \pi} n_{{\rm c0}}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2} \over {3({\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}}} \right]^{1/2}},$$

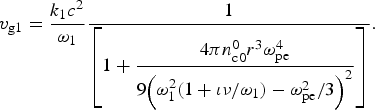(4)$${v_{{\rm g}1}} = \displaystyle{{{k_1}{c^2}} \over {{{\rm \omega} _1}}}\displaystyle{1 \over {\left[ {1 + \displaystyle{{4{\rm \pi} n_{{\rm c0}}^{0} {r^3}{\rm \omega} _{{\rm pe}}^4} \over {9{{\left( {{\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3} \right)}^2}}}} \right]}}.$$

Here ${{\rm \omega} _{\rm p}} = \sqrt {4{\rm \pi} n_{{\rm 00}}^{0} {e^2}/m{{\rm \gamma} _{0}}} $ is the frequency of plasma electrons, ${{\rm \omega} _{{\rm pe}}} = \sqrt {4{\rm \pi} {n_{\rm e}}{e^2}/m{{\rm \gamma} _{0}}} $ is the plasma frequency inside the cluster, ν is the collisional frequency inside the cluster, −e and m are electronic charge and rest mass, respectively, and γ₀ is the average value of relativistic factor, given as ${{\rm \gamma} _{0}} \approx {(1 + a_{0}^2 /2)^{1/2}}$, a ₀ = eA₀/mω₁c, a ₀ < 1.

When an intense ultra short laser pulse interacts with cluster, the cluster gets ionized. So a highly excited cluster consists of plasma with electrons and multicharged atomic ions. We assume this ionization to be homogeneous across the whole cluster volume so that we can consider the model of ionized cluster as two homogeneously charged spheres: One is positively charged and the other is negatively charged. The center of negatively charged sphere is shifted along the x-axis by a distance x with respect to center of positively charged sphere. The restoring force experienced by the cluster electrons is given as

(5)$${\vec F_{\rm T}} = \displaystyle{{ - 4{\rm \pi}} \over 3}{n_{\rm e}}{e^2}\vec x - e{\vec E}_1$$

As the cluster expands, its size increases and average electron density inside it decreases. We consider the case when the plasma frequency ω_pe has gone down significantly. From the equation of motion of cluster electrons, their oscillatory velocity can be written as,

(6)$${\vec v_{{\rm c}1}} = \displaystyle{{ - {\rm \iota} e{{\rm \omega} _1}{{\vec E}_1}} \over {m{{\rm \gamma} _{0}}[{\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}}.$$

Similarly from the equation of motion of plasma electrons, their oscillatory velocity can be written as,

(7)$${\vec v_1} = \displaystyle{{e{{\vec E}_1}} \over {m{{\rm \gamma} _{0}}{\rm \iota} {{\rm \omega} _1}}}.$$

The wave vector ${\vec k}_1$ of the fundamental laser increases more than linearly with the frequency ω₁ hence, ${\vec k}_3\gt 3{{\vec k}_1} $; that is, the momentum $\hbar {\vec k_{3}}$ of a third harmonic photon is greater than the sum of the momenta of three pump photons $3\hbar {k_1}$. Hence the additional momentum is required to satisfy the phase matching condition. The density ripple provides this additional momentum to third harmonic photon to make the process resonant. For this the wave number k ₀ should be as, ${\vec k}_0 = {\vec k}_{3}-3{\vec k}_1$. The laser exerts a ponderomotive force ${\vec F_2} = ( - e/2c)({\vec v_{{\rm c}1}} \times {\vec B_1})$ on cluster electrons at $(2{{\rm \omega} _1},2{\vec k}_1)$. This produces an oscillatory velocity,

(8)$$\eqalign{{\vec v}_{{\rm c}2} = & \displaystyle{{{{\rm \omega}_1}{e^2}{k_1}A_1^2} \over {{m^2}{{\rm \gamma} _{0}}[{\rm \omega}_1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}} \cr \quad & \displaystyle{{{e^{ - \iota [2{{\rm \omega}_{1}}t - 2{k_{1}}z]}}} \over {[4{\rm \omega} _1^2 (1 + {\rm \iota} \nu /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}}{\hat z}.} $$

Using ${\vec v_{{\rm c}2}}$ in the equation of continuity, we obtain the nonlinear density perturbation at (2k ₁ + k ₀),

(9)$$n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_{0}}}^{{\rm NL}} = \displaystyle{{{{\vec v}_{{\rm c}2}}.(\vec 2{k_1} + {{\vec k}_{0}}){n_{\rm a}}} \over {2{{\rm \omega} _1}}},$$

where n _a = (4π/3)n _en _cr ³ is the average number of cluster electrons per unit volume.

Using Eq. (8) in Eq. (9) we get,

(10)$$\eqalign{n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_{0}}}^{{\rm NL}} = & \displaystyle{{{e^2}{k_1}(\vec 2{k_1} + {{\vec k}_{0}}){n_{\rm a}}A_1^2} \over {2{m^2}{{\rm \gamma} _{0}}[{\rm \omega} _1^2 (1 + {\rm \iota \nu} /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}} \cr \quad & \displaystyle{{{e^{ - \iota [2{{\rm \omega} _1}t - 2{k_1}z]}}} \over {[4{\rm \omega} _1^2 (1 + {\rm \iota \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}}.} $$

This nonlinear density perturbation at (2ω,2k ₁ + k ₀) causes electrostatic perturbation of potential ϕ₂ as, ${{\rm \phi} _2} = $${{\rm \phi} _2}{e^{ - \iota [2{{\rm \omega} _1}t - (2{k_1} + {k_{0}})z]}}$, which produces a self-consistent space charge field ${\vec E_2} = - \vec \nabla {{\rm \phi} _2}$. This space charge field produces linear density perturbation in cluster electrons as,

(11)$$n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_{0}}}^{\rm L} = \displaystyle{{{{(2{k_1} + {k_{0}})}^2}{{\rm \chi} _{c2}}{{\rm \phi} _2}} \over {4{\rm \pi} e}},$$

where 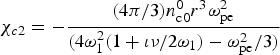${{\rm \chi} _{c2}} = - \displaystyle{{(4{\rm \pi} /3)n_{{\rm c0}}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2} \over {(4{\rm \omega} _1^2 (1 + {\rm \iota} \nu /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}}$.

Also the non-linear density perturbation in plasma electrons is

(12)$$n_{{\rm p}2{\rm \omega}, 2{k_{1}} + {k_0}}^{{\rm NL}} = \displaystyle{{{e^2}{k_1}(\vec 2{k_1} + {{\vec k}_0}){n_{0}}A_1^2 {e^{ - \iota [2{{\rm \omega} _{1}}t - 2{k_{1}}z]}}} \over {8{m^2}{{\rm \gamma} _{0}}{\rm \omega} _1^4}}. $$

Now from Poisson's equation ${\nabla ^2}{{\rm \phi} _2} = 4{\rm \pi} e(n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_{0}}} + n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_{0}}} )$, we get

(13)$${\rm \phi}_2 = \displaystyle{{ - 4{\rm \pi} e(n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_{0}}}^{{\rm NL}} + n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_{0}}}^{{\rm NL}} )} \over {{\rm \epsilon} _2^{\prime} {{(2{k_1} + {k_{\rm o}}{\rm )}}^2}}},$$

where ${\rm \epsilon} _2^{\prime} = 1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 - (4{\rm \pi} /3)n_{{\rm c0}}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2 /(4{\rm \omega} _1^2 (1 + {\rm \iota} {\rm \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)$.

Hence the net density of cluster electrons can be written as,

(14)$$\eqalign{{n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}} = & \; n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} + n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}^{\rm L} \cr = &\; n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} \displaystyle{{(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 )} \over {{\rm \epsilon} _2^{\prime}}} \cr & \quad + n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} \displaystyle{{(4{\rm \pi} /3)n_{{\rm c0}}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2} \over {(4{\rm \omega} _1^2 (1 + {\rm \iota \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3){\rm \epsilon} _2^{\prime}}},} $$

where $n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} $ and $n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} $ are given by Eqs. (10) and (12), respectively.

Similarly the net density of plasma electrons will be

(15)$$\eqalign{{n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_0}}} = & \; n_{{\rm p}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} \left( {1 + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \omega} _{1}^{\rm 2} {\rm \epsilon} _2^{\prime}}}} \right) \cr & \quad + n_{{c}2{\rm \omega}, 2{k_1} + {k_0}}^{{\rm NL}} \left( {\displaystyle{{{\rm \omega} _{\rm p}^2} \over {4{\rm \omega} _1^2 {\rm \epsilon} _2^{\prime}}}} \right).} $$

The second-order oscillatory velocity ${\vec v_{{\rm c}2}}$ of cluster electrons beats with first-order magnetic field B ₁ to exert a ponderomotive force at (3ω₁, $3{\vec k}_1$) that is, ${\vec F_3} = ( - e/2c)({\vec v_{{\rm c}2}} \times {\vec B_1})$. This force produces a third-order oscillatory velocity,

(16)$$\eqalign{{{\vec v}_{{\rm c}3}} = & \displaystyle{{ - 3\iota {{\rm \omega} _1}{e^3}k_1^2 A_1^3} \over {2{m^3}{{\rm \gamma} _{\rm o}}[{\rm \omega} _1^2 (1 + {\rm \iota \nu} /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}} \cr & \quad \displaystyle{{{e^{ - \iota [3{{\rm \omega} _1}t - 3{k_1}z]}}} \over {[4{\rm \omega} _1^2 (1 + {\rm \iota \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}} \cr & \quad \displaystyle{1 \over {[9{\rm \omega} _1^2 (1 + {\rm \iota \nu} /3{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}}\hat x.} $$

The third harmonic nonlinear current density due to atomic cluster at (3ω₁, $3{\vec k}_1 + {\vec k}_0$) is,

(17)$$\eqalign{\vec J\hskip1pt_{{\rm c}3}^{{\rm NL}} = & - {n_{\rm a}}e{{\vec v}_{{\rm c}3}} - \displaystyle{{{n_{{\rm c}2{\rm \omega}, 2{k_1} + {k_0}}}e{{\vec v}_{{\rm c}1}}} \over 2} \cr = & \displaystyle{{{\rm \iota} {\rm \pi} n_{\rm c}^{0} {n_{\rm e}}{r^3}{{\rm \omega} _1}{e^4}{k_1}A_1^3} \over {{m^3}{{\rm \gamma} _{0}}\left[ {{\rm \omega} _1^2 (1 + {\rm \iota \nu} /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^{\rm 2} /3} \right]}} \cr & \quad \displaystyle{{{e^{ - \iota [3{{\rm \omega} _{1}}t - (3{k_1} + {k_0})z]}}} \over {\left[ {4{\rm \omega} _1^2 (1 + {\rm \iota \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3} \right]}} \cr & \quad \left[ {\displaystyle{{2{k_1}} \over {\left[ {9{\rm \omega} _1^2 (1 + {\rm \iota \nu} /3{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3} \right]}}} \right. \cr & \quad + \displaystyle{{(2{k_1} + {k_0})(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 )} \over {3{{\rm \gamma} _{\rm o}}\left[ {{\rm \omega} _1^2 (1 + {\rm \iota \nu} /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3} \right]{\rm \epsilon} _2^{\prime}}} \cr & \quad + \left. {\displaystyle{{{\rm \pi} n_{0}^{0} (2{k_1} + {k_0}){e^2}} \over {3m{{\rm \gamma} _{0}}{\rm \omega} _1^4 {\rm \epsilon} _2^{\prime}}}} \right]\hat x.} $$

Similarly we can obtain third harmonic nonlinear current density due to plasma electrons at (3ω₁, $3{\vec k}_1 + {\vec k}_0$) as,

(18)$$\eqalign{\vec J\hskip1.7pt_{{\rm p}3}^{{\rm NL}} = & \displaystyle{{{\rm \iota} n_{0}^{0} {e^4}{k_1}A_1^3 {e^{ - {\rm \iota} [3{{\rm \omega} _1}t - (3{k_1} + {k_0})z]}}} \over {8{m^3}{{\rm \gamma} _{0}}{\rm \omega} _1^5}} \cr & \quad \left[ {\displaystyle{{{k_1}} \over 3} + \displaystyle{{(2{k_1} + {k_0})(1 + {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 {\rm \epsilon} _2^{\prime} )} \over {2{{\rm \gamma} _{\rm o}}}}} \right. \cr & \quad + \displaystyle{{2{\rm \pi} {n_{\rm a}}{e^2}{\rm \omega} _{1}^{\rm 2}} \over {m{{\rm \gamma} _{0}}[{\rm \omega} _1^2 (1 + {\rm \iota \nu} /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3]}} \cr & \quad \left. {\displaystyle{{(2{k_1} + {k_{0}})} \over {[4{\rm \omega} _1^2 (1 + {\rm \iota \nu} /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^{\rm 2} /3]{\rm \epsilon} _2^{\prime}}}} \right]\hat x.} $$

The self-consistent field ${\vec E_3}$ of laser imparts an oscillatory velocity $\vec {v}_3^{\,L} = e{\vec E_3}/m{{\rm \gamma} _{0}}{\rm \iota} 3{{\rm \omega} _1}$ to plasma electrons at frequency 3ω₁ and linear current density at third harmonic due to this field is,

(19)$$\vec J_{{\rm p}3}^{\,\rm L} = \displaystyle{{ - n_{0}^{0} {e^2}{{\vec E}_3}} \over {m{{\rm \gamma} _{0}}{\rm \iota} 3{{\rm \omega} _1}}}.$$

Hence net current density becomes, ${\vec J_3} = \vec J_{{\rm p}3}^{\,\rm L} + \vec J_{{\rm p}3}^{{\,\rm NL}} + \vec J_{{\rm c}3}^{{\,\rm NL}} $.

3. THIRD HARMONIC FIELD

The wave equation for third harmonic field E ₃ can be derived from Maxwell's equations as,

(20)$${\nabla ^2}{\vec E_3} = \displaystyle{{4{\rm \pi}} \over {{c^2}}}\displaystyle{{\partial {{\vec J}_3}} \over {\partial t}} + \displaystyle{1 \over {{c^2}}}\displaystyle{{{\partial ^2}{{\vec E}_3}} \over {\partial {t^2}}}$$

Using ${\vec J_3}$ from Eqs. (17)–(19), the wave equation becomes,

(21)$$\eqalign{& \displaystyle{{{\partial ^2}{{\vec E}_3}} \over {\partial {z^2}}} - \displaystyle{1 \over {{c^2}}}\displaystyle{{{\partial ^2}{{\vec E}_3}} \over {\partial {t^2}}} - \displaystyle{{4{\rm \pi}} \over {{c^2}}}\displaystyle{{\partial \vec J_{{\rm p}3}^{\,\rm L}} \over {\partial t}} \cr & = {\rm \alpha} A_1^3 {e^{ - \iota [3{{\rm \omega} _{1}}t - (3{k_1} + {k_{0}})z]}}\hat x} $$

where

(22)$$\eqalign{{\rm \alpha} = & \displaystyle{{ - 12{\rm \pi} {\rm \iota} {{\rm \omega} _1}} \over {{c^2}}}\cr & \left[ {\displaystyle{{{\rm \iota} {\rm \pi} n_{\rm c}^{0} {n_{\rm e}}{r^3}{\omega _1}{e^4}{k_1}} \over {{m^3}{{\rm \gamma} _{0}}({\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}}} \right.\, \displaystyle{1 \over {(4{\rm \omega} _1^2 (1 + {\rm \iota} \nu /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}} \cr & \left\{ {\displaystyle{{2{k_1}} \over {(9{\rm \omega} _1^2 (1 + {\rm \iota} \nu /3{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}}} \right. + \displaystyle{{(2{k_1} + {k_{0}})(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 )} \over {3{{\rm \gamma} _{0}}({\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3){\rm \epsilon} _2^{\prime}}} \cr & \left. { + \displaystyle{{{\rm \pi} n_{0}^{0} (2{k_1} + {k_{0}}){e^2}} \over {3m{{\rm \gamma} _{0}}{\rm \omega} _1^4 {\rm \epsilon} _2^{\prime}}}} \right\} + \displaystyle{{{\rm \iota} n_{0}^{0} {e^4}{k_1}} \over {8{m^3}{\rm \gamma _0\omega} _1^5}} \cr &\left\{ {\displaystyle{{{k_1}} \over 3}} \right. + \displaystyle{{(2{k_1} + {k_{0}})(1 + {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 {\rm \epsilon} _2^{\prime} )} \over {2{{\rm \gamma} _{0}}}} \cr & + \displaystyle{{{2\rm \pi} {n_{\rm a}}{e^2}{\rm \omega} _1^2} \over {m{{\rm \gamma} _{0}}({\rm \omega} _1^2 (1 + {\rm \iota} \nu /{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3)}} \cr & \left. {\left. {\displaystyle{{(2{k_1} + {k_{0}})} \over {(4{\rm \omega} _1^2 (1 + {\rm \iota} \nu /2{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /3){\rm \varepsilon} _2^{\prime}}}} \right\}} \right].} $$

We assume the solution of Eq. (21) as

(23)$${\vec E_3} = \hat x{A_3}(z,t){e^{ - \iota [3{{\rm \omega} _{1}}t - (3{k_1} + {k_0})z]}}$$

Using Eqs. (21) and (23), we obtain

(24)$$\eqalign{\displaystyle{{\partial {A_3}} \over {\partial z}} + & \displaystyle{{3{{\rm \omega} _1}} \over {{c^2}{k_3}}}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {18{\rm \omega} _1^2}(1+iv/3 {\rm \omega}_1)}} \right)\displaystyle{{\partial {A_3}} \over {\partial t}} \cr & - \displaystyle{{2\iota {\rm \pi} n_{\rm c}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2} \over {3{k_3}{c^2}((1 + {\rm \iota} \nu /3{{\rm \omega} _1}) - {\rm \omega} _{{\rm pe}}^2 /27{\rm \omega} _1^2 )}}{A_3} \cr & = {{\rm \alpha} _3}{[F(z - {v_{{\rm g}1}}t)]^3}} $$

where ${{\rm \alpha} _3}\, = \,{\rm \alpha} /2{\rm \iota} {k_3}$.

Using the transformations ζ = z − v_g1t and η = z, we get,

(25)$$\displaystyle{{\partial {A_3}} \over {\partial \rm \eta}} + {\rm \beta} \displaystyle{{\partial {A_3}} \over {\partial {\rm \zeta}}} - q{A_3} = {{\rm \alpha} ^{\prime}_3}{A_{0}}{\rm exp}\left( {\displaystyle{{ - 3{{\rm \zeta} ^2}} \over {{\rm \zeta} _{0}^2}}} \right)$$

where 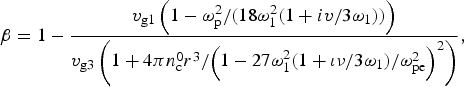${\rm \beta} = 1 - \displaystyle{{{v_{{\rm g1}}}\left( {1 - {\rm \omega} _{\rm p}^2 /(18{\rm \omega} _1^2 (1+iv/3 {\rm \omega}_1))} \right)} \over {{v_{{\rm g}3}}\left( {1 + 4{\rm \pi} n_{\rm c}^{0} {r^3}/{{\left( {1 - 27{\rm \omega} _1^2 (1 + {\rm \iota} \nu /3{{\rm \omega} _1})/{\rm \omega} _{{\rm pe}}^2} \right)}^2}} \right)}},$$

$$q = 2{\rm \iota \pi }n_{\rm c}^{0} {r^3}{\rm \omega }_{{\rm pe}}^2 /3{k_3}{c^2}((1 + {\rm \iota }\nu /3{{\rm \omega }_1}) - {\rm \omega }_{{\rm pe}}^2 /27{\rm \omega }_1^2 )$$

and 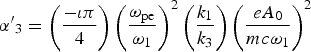${{\rm \alpha '}_3} = \left( {\displaystyle{{ - {\rm \iota} {\rm \pi}} \over 4}} \right){\left( {\displaystyle{{{{\rm \omega} _{{\rm pe}}}} \over {{{\rm \omega} _1}}}} \right)^2}\left( {\displaystyle{{{k_1}} \over {{k_3}}}} \right){\left( {\displaystyle{{e{A_0}} \over {mc{{\rm \omega} _1}}}} \right)^2}$$

$$\eqalign{& \displaystyle{{n_{\rm c}^{0} {r^3}{k_1}} \over {\left( {(1 + {\rm \iota }\nu /{{\rm \omega }_1}) - {\rm \omega }_{{\rm pe}}^2 /3{\rm \omega }_1^2 } \right)\left( {(1 + {\rm \iota }\nu /2{{\rm \omega }_1}) - {\rm \omega }_{{\rm pe}}^2 /12{\rm \omega }_1^2 } \right)}} \cr & \left[ {\displaystyle{1 \over {3((1 + {\rm \iota }\nu /3{{\rm \omega }_1}) - {\rm \omega }_{{\rm pe}}^2 /27{\rm \omega }_1^2 )}}} \right. \cr & + \displaystyle{{(1 + {k_{0}}/2{k_1})(1 - {\rm \omega }_{\rm p}^2 /4{\rm \omega }_1^2 )} \over {{{\rm \gamma }_{0}}\left( {(1 + {\rm \iota }\nu /{{\rm \omega }_1}) - {\rm \omega }_{{\rm pe}}^2 /3{\rm \omega }_1^2 } \right){\rm \epsilon }_2^{\prime} }} \cr & \left. { + \displaystyle{{(1 + {k_{0}}/2{k_1})({{\rm \omega }_{\rm p}}/{{\rm \omega }_1}{)^2}} \over {2{{\rm \gamma }_{0}}{\rm \epsilon }_2^{\prime} }}} \right] \cr & {\rm + }\left( {\displaystyle{{ - 3\iota } \over 8}} \right){\left( {\displaystyle{{{{\rm \omega }_{\rm p}}} \over {{{\rm \omega }_1}}}} \right)^2}\left( {\displaystyle{{{k_1}} \over {{k_3}}}} \right){\left( {\displaystyle{{e{A_{\rm o}}} \over {mc{{\rm \omega }_1}}}} \right)^2} \cr & \displaystyle{{{k_1}}} {\left[ {\displaystyle{1 \over 6}} \right. \left. { + \displaystyle{{(1 + {k_{0}}/2{k_1})(1 + {\rm \omega }_{\rm p}^2 /4{\rm \omega }_1^2 {\rm \epsilon }_2^{\prime} )} \over {2{{\rm \gamma }_{0}}}}} \right].}} $$

For Gaussian profile, we can use $F(z - {v_{{\rm g}1}}t) = {A_{\rm o}}{\rm exp}( - {k_i}{\rm \eta }){\rm exp(} - {{\rm \zeta }^2}/{\rm \zeta }_{0}^2 {\rm )}$, where ζ₀ = τ₀v _g1 is initial laser pulse length and τ₀ is laser pulse duration. Following Liu and Parashar (Reference Liu and Parashar2007), k _i the absorption coefficent can be written as

(26)$${k_i} = \displaystyle{{2{\rm \pi}} \over 3}\displaystyle{{{{\rm \omega} _1}} \over c}\displaystyle{{n_{\rm c}^{0} {r^3}{\rm \omega} _{{\rm pe}}^2 \nu /{\rm \omega} _1^3} \over {{{[1 - ({\rm \omega} _{{\rm pe}}^2 /3{\rm \omega} _1^2 )(1 + {{\rm \eta} _1}/f\,{)^{ - 3}}]}^2} + {{[\nu /{{\rm \omega} _1}]}^2}}}$$

where ${{\rm \eta} _1} = \sqrt {({Z_i}\nu {{\rm \tau} _{0}}m)/(2{m_i})} (e{A_{0}}t)/(m{\rm \omega} fr)$$

$$1/(1 + {\rm \iota }\nu /{{\rm \omega }_1} - {\rm \omega }_{{\rm pe}}^2 /3{\rm \omega }_1^2 {)^2}.$$

Here Z _i is the charge state of cluster atom, m _i is mass of ion and f is beam width parameter.

From the solution of Eq. (25), normalized third harmonic wave amplitude can be deduced as,

(27)$$\eqalign{& \displaystyle{{ \vert {A_3} \vert} \over { \vert {A_0} \vert}} = \left \vert {\displaystyle{{{e^{ - {k_i}{\rm \eta}}} {e^{q{\rm \zeta} /{\rm \beta}}} {{{\rm \alpha ^{\prime}}}_3}{e^{{q^2}{\rm \zeta} _{0}^2 /12{{\rm \beta} ^2}}}\sqrt {3{\rm \pi}} {{\rm \zeta} _{0}}} \over {6{\rm \beta}}}} \right. \cr & \quad \quad \quad \left[ {{\rm erf}\left( {\displaystyle{{6{\rm \beta \zeta} + q{\rm \zeta} _{0}^2} \over {2\sqrt 3 {\rm \beta} {{\rm \zeta} _{0}}}}} \right)} \right. \cr & \quad \quad \quad \left. {\left. { - {\rm erf}\left( {\displaystyle{{6{\rm \beta} ({\rm \zeta} - {\rm \beta \eta} ) + q{\rm \zeta} _{0}^2} \over {2\sqrt 3 {\rm \beta} {{\rm \zeta} _{0}}}}} \right)} \right]\;} \right \vert,} $$

where erf(ϕ) is error function of argument ϕ. Or

(28)$$\eqalign{& \displaystyle{{ \vert {A_3} \vert} \over { \vert {A_0} \vert}} = \left \vert {\displaystyle{{{e^{ - {k_i}z^{\prime}{{\rm \zeta} _{0}}}}{e^{(q{{\rm \zeta} _{0}}(z^{\prime} - t^{\prime})/{\rm \beta})}} {{{\rm \alpha ^{\prime}}}_3}{e^{{q^2}{\rm \zeta} _{0}^2 /12{{\rm \beta} ^2}}}\sqrt {3{\rm \pi}} {{\rm \zeta} _0}} \over {6{\rm \beta}}}} \right. \cr & \quad \quad \quad \left[ {{\rm erf}\left( {\sqrt 3 (z^{\prime} - t^{\prime}) + \displaystyle{{q{{\rm \zeta} _{0}}} \over {2\sqrt 3 {\rm \beta}}}} \right)} \right. \cr & \quad \quad \quad \left. {\left. { - {\rm erf}\left( {\sqrt 3 ((z^{\prime} - t^{\prime}) - {\rm \beta} z^{\prime}) + \displaystyle{{q{{\rm \zeta} _{0}}} \over {2\sqrt 3 {\rm \beta}}}} \right)} \right]\;} \right \vert} $$

where z′ = z/ζ₀ and t′ = v _g1t/ζ₀.

The third harmonic Poynting vector can be written as

(29)$${\vec P_3} = \displaystyle{c \over {8{\rm \pi}}} \vec E_3^{\rm \star} \times {\vec H_3} = \displaystyle{{{c^2}} \over {24{\rm \pi} {{\rm \omega} _1}}}(3{\vec k}_1 + {\vec k_{0}}) \vert {A_3}{ \vert ^2}.$$

Also the Poynting vector for the fundamental wave can be written as

(30)$${\vec P_1} = \displaystyle{c \over {8{\rm \pi}}} \vec E_1^{\rm \star} \times {\vec H_1} = \displaystyle{{{c^2}} \over {8{\rm \pi} {{\rm \omega} _1}}}{\vec k}_1 \vert {A_1}{ \vert ^2}.$$

From Eqs. (29) and (30), we get efficiency of third harmonic generation as,

(31)$$\left \vert {\displaystyle{{{{\vec P}_3}} \over {{{\vec P}_1}}}} \right \vert = \displaystyle{1 \over 3}(3 + {k_{0}}/{k_1}){\left \vert {\displaystyle{{{{\vec A}_3}} \over {{{\vec A}_{0}}}}} \right \vert ^2}{e^{-2{{\rm \zeta} ^2}/{{\rm \zeta} _0}^2}}. $$

4. NUMERICAL RESULTS and DISCUSSION

We have solved Eq. (28) numerically for the following set of parameters: Laser frequency ω₁ = 2.126 × 10¹⁵ rad/s, laser intensity I ≈ 10¹⁷ W/cm², laser pulse duration τ₀ = 100 fs, plasma frequency ω_p = 1.256 × 10¹⁴, plasma frequency inside the cluster ω_pe = 7.565 × 10¹⁵ rad/s, initial ripple density of plasma electrons $n_{0}^{0} = 5 \times {10^{18}}\;{\rm c}{{\rm m}^{ - 3}}$, free electron density inside the cluster n _e ≈ 1.8 × 10²² and ν/ω₁ = 0.01. 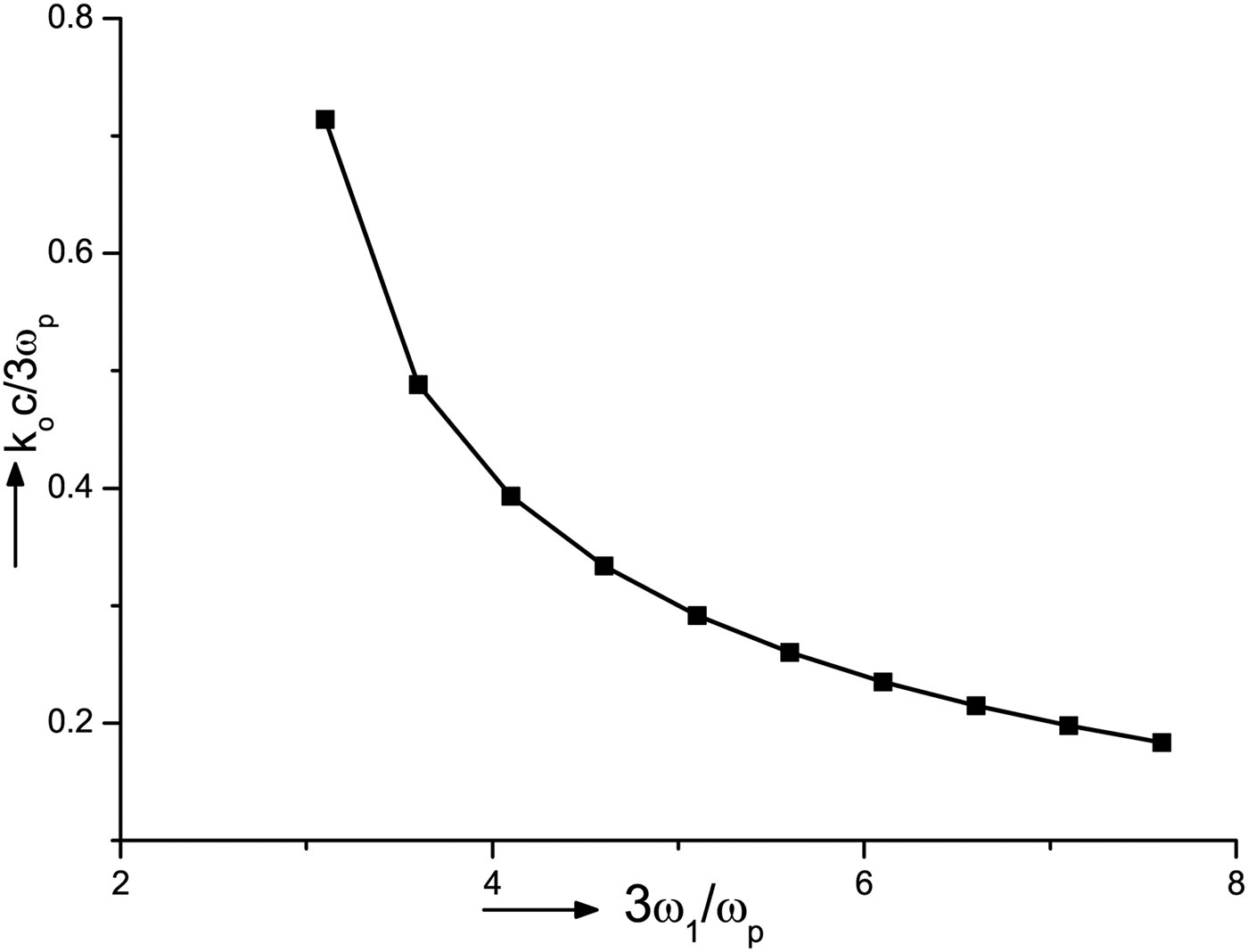We consider Ar cluster of size r = 100 Å with density $n_{\rm c}^{0} = $$2 \times {10^{14}}\;{\rm c}{{\rm m}^{ - 3}}$. In Figure 1, we have plotted normalized wave number of density ripple, k ₀c/ω_p with normalized third harmonic frequency 3ω₁/ω_p for $n_{\rm c}^{0} {r^3} = 2 \times {10^{ - 4}}$. The normalized wave number of density ripple required for phase matching, decreases with the increase in third harmonic frequency. Figure 2 shows the variation of normalized third harmonic wave amplitude |A ₃|/|A ₀| with normalized distance of propagation z′ for different values of intensity parameter a ₀ = eA ₀/mω₁c = 0.1, 0.15, 0.2. The other parameters are ω_pe/ω₁ = 3.558, $n_{\rm c}^{0} {r^3}\, = \,2 \times {10^{ - 4}}$, t′ = 4, f = 1 and $\sqrt {{Z_i}m/{m_i}} {{\rm \omega} _{{\rm pe}}}t = 60$. The third harmonic amplitude increases sharply at z′ =4. For z′ =4 in Eq. (28), the exponential term tends to zero and it gives the maximum amplitude of generated third harmonic wave. It is clear from Figure 2 that as we increase the value of a ₀ from 0.1 to 0.2, the normalized third harmonic amplitude increases from 0.0090 to 0.0362. The normalized amplitude of the third harmonic also depends upon cluster size and increases with increase in the cluster size at a ₀ = 0.2, as depicted in Figure 3. Since atomic clusters are very efficient at absorbing laser energy, so it would be significant to study the effect of laser absorption on third harmonic wave amplitude. Hence in Figure 4 we plot normalized third harmonic wave amplitude with normalized distance of propagation for different values of normalized collisional frequency ν/ω₁ = 0.01, 0.02, 0.03. In this plot we observe that if we increase the collision frequency then the laser absorption increases and correspondingly amplitude of third harmonic wave decreases significantly. Therefore, at low value of collisional frequency one can get higher efficiency of third harmonic generation. Figure 5 shows the variation of normalized amplitude of the fundamental wave and third harmonic wave with normalized distance of propagation for different values of normalized time t′ = 2, 3, and 4 at a ₀ = 0.2. The other parameters are same as taken in Figure 2. It is clear from Figure 5 that initially the third harmonic wave is generated in the domain of the fundamental laser pulse and as time passes, it starts slipping out of the domain of fundamental laser pulse and its amplitude increases with time. Our results are in contrast in case of plasma where the amplitude of generated harmonic wave saturates with time (Kant & Sharma, Reference Kant and Sharma2004; Rajput et al., Reference Rajput, Kant, Singh and Nanda2009; Kumar et al., Reference Kumar, Rajouria and Magesh Kumar2013). It is due to the group velocity mismatch between the fundamental laser and third harmonic pulse. The group velocity of third harmonic pulse is greater than that of fundamental laser pulse which causes pulse slippage of third harmonic pulse. Figure 6 shows the variation of normalized third harmonic wave amplitude |A ₃|/|A ₀| with normalized third harmonic frequency. One can clearly see from the figure that initially the third harmonic amplitude increases gradually with third harmonic frequency and after 3ω₁/ω_p = 16 it increases rapidly.

Fig. 1. Variation of normalized wave number of density ripple k ₀c/ω_p with normalized third harmonic frequency 3ω₁/ω_p for the following set of parameters, ω_pe = 7.565 × 10¹⁵ rad/s, $n_{\rm c}^{0} {r^3} = 2 \times {10^{ - 4}}$, and ω_p = 1.256 × 10¹⁴ rad/s.

Fig. 2. Variation of normalized third harmonic wave amplitude |A ₃|/|A ₀| with normalized distance of propagation z′ for different values of normalized intensity parameter a ₀ with ω_pe/ω₁ = 3.558, $n_{\rm c}^{0} {r^3} = 2 \times {10^{ - 4}}$, ν/ω₁ = 0.01, ω₁ = 2.126 × 10¹⁵ rad/s, ω_p = 1.256 × 10¹⁴ rad/s, τ₀ = 100 fs, and t′ = 4.

Fig. 3. Variation of normalized third harmonic wave amplitude |A ₃|/|A ₀| with normalized distance of propagation z′ for different values of cluster radius r and fixed value of a ₀ = 0.2. The other parameters are same as taken in Figure 2.

Fig. 4. Variation of normalized third harmonic and fundamental wave amplitude with normalized distance of propagation z′ for different value of normalized collisional frequency ν/ω₁ and fixed value of a ₀ = 0.2. The other parameters are same as taken in Figure 2.

Fig. 5. Variation of normalized third harmonic and fundamental wave amplitude with normalized distance of propagation z′ for different value of t′ and fixed value of a ₀ = 0.2. The other parameters are same as taken in Figure 2.

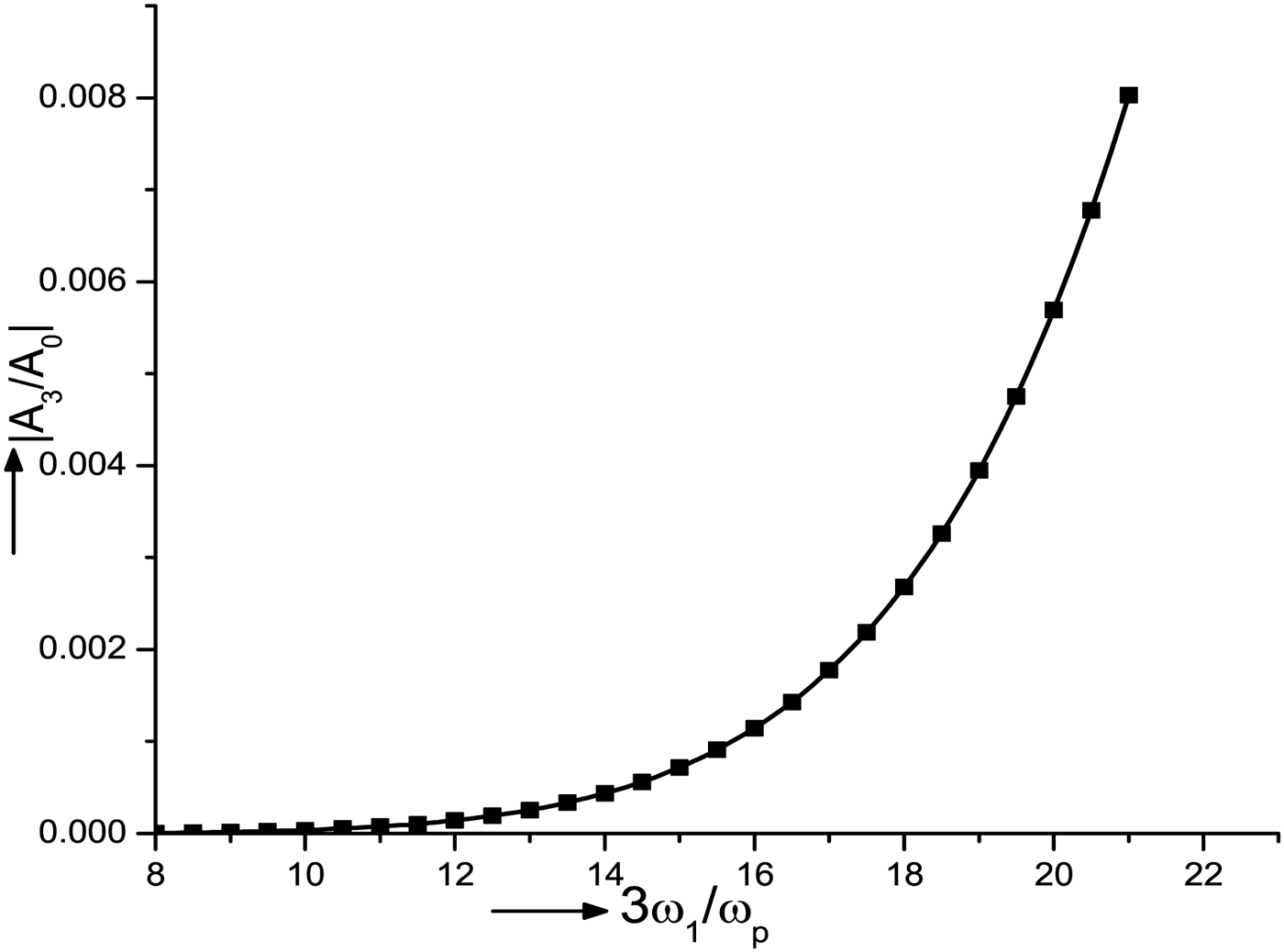
Fig. 6. Variation of normalized third harmonic amplitude |A ₃|/|A ₀| with normalized third harmonic frequency 3ω₁/ω_p at a ₀ = 0.2 and z′ = 4 for the same parameters as taken in Figure 2.