1. INTRODUCTION
Acceleration of electrons from short-pulse and high-intense laser (≥1018 W/cm2) interacting with plasmas is an important issue for electron accelerators (Hora et al., Reference Hora, Hoelss, Scheid, Wang, Ho, Osman and Castillo2000; Joshi & Katsouleas, Reference Joshi and Katsouleas2003; Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccheerini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholz, Schiavi and Willi2007; Esarey et al., Reference Esarey, Schroeder, Cormier-Michel, Shadwick, Geddes and Leemans2007; Gupta & Suk, Reference Gupta and Suk2007; Karmakar & Pukhov, Reference Karmakar and Pukhov2007; Xu et al., Reference Xu, Kong, Chen, Wang, Wang, Lin and Ho2007; Zhou et al., Reference Zhou, Yu and He2007) and the fast ignition scheme (Tabak et al., Reference Tabak, Ammer, Glinsky, Kruer, Wilke, Woodworth, Campbell and Perry1994; Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tamaka, Toyama, Yamanaka and Zepf2001; Nuckolls et al., Reference Nuckolls and Wood2002; Hora, Reference Hora2007a, Reference Hora, Badziak, Read, Li, Liang, C Ang, Liu Hong, Zheng-Ming, Zhang, Osmanm, Mi-Ley, Zhang, He, Peng, Glowacz, Jablonski, Wolowski, Skladanovski, Jungwirth, Rohlena and Ulschmied2007b) or beam fusion (Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosemej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005). Recently, different acceleration mechanisms have been investigated for laser interaction with both underdense and overdense plasmas (Gibbon, Reference Gibbon2005; Salamin et al., Reference Salamin, Hu, Hatsagortsyan and Keitel2006; Stait-Gardner & Castillo, Reference Stait-Gardner and Castillo2006; Zhou et al., Reference Zhou, He and Yu2006). The idea of using the plasma wave excited by an intense laser to accelerate electrons was first suggested by Tajima and Dawson (Reference Tajima and Dawson1979) more than 20 years ago. In the so-called standard laser wakefield acceleration scheme, the wake plasma wave is most efficiently generated by the ponderomotive force of the laser pulse when its duration τL is close to half of the plasma wave period (Hamster et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993; Siders et al., Reference Siders, Leblanc, Fisher, Tajima, Downer, Babine, Stepanov and Sergeev1996). This is the same as acceleration of electrons in vacuum by the electromagntic laser field (Evans, Reference Evans1988; Hora, Reference Hora1988) where it was confirmed that the highest acceleration is achieved with half optical waves or “rectified waves” (Scheid & Hora, Reference Scheid and Hora1989, Hora et al., Reference Hora, Osman, Castillo, Collins, Stait-Gardener, Chan, Hölss, Scheid, Wang and Ho2002).
On the other hand, the nonlinear ponderomotive force also plays an important role in direct laser acceleration (Mckinstrie & Startsev, Reference Mckinstrie and Startsev1996; Quesnel & Mora, Reference Quesnel and Mora1998; Stupakov & Zolotorev, Reference Stupakov and Zolotorev2001; Schmitz & Kull, Reference Schmitz and Kull2002; Kong et al., Reference Kong, Miyazaki, Kawata, Miyauchi, Nakajima, Masuda, Miyanaga and Ho2003). At high laser intensities, the relativistic motion starts to operate, causing the electron to be directed forward as well as sideways, and forming laser-plasma channels. It is known that ponderomotive expulsion of background plasma electrons from such plasma channels creates a radial quasistatic electric (QSE) field Es, and the current of electrons accelerated by axial ponderomotive force generates the azimuthal quasistatic magnetic (QSM) field Bsθ. For a linearly polarized (LP) laser, both fields trap a relativistic electron in the channel and result in its betatron oscillation along the laser polarization. Therefore, an electron undergoes a strong downshifted optical frequency when it is accelerated in the laser propagation direction. As a result, the transverse betatron oscillation may be in resonance with the LP laser if the downshift is strong enough (Pukhov et al., Reference Pukhov, Sheng and Meyer-terr-vehn1999; Tsakiris et al., Reference Tsakiris, Gahn and Tripathi2000; Yu et al., Reference Yu, Yu, Chen, Zhang, Yin, Cao, Lu and Xu2003; Liu & Tripathi, Reference Liu and Tripathi2005, Reference Liu, He and Hora2006), leading to a considerable acceleration of electrons.
However, the interaction of a circularly polarized (CP) laser with plasma can additionally generate an axial QSM field Bsz due to the rotational motion of relativistic electrons, besides the radial QSE field Es and the azimuthal QSM field Bsθ. The field Bsz may effectively trap and collimate the accelerated electrons. Consequently, the accelerated electrons driven by CP laser may have a smaller divergent angle than using LP laser (Sheng & Meyer-ter-vehn, Reference Sheng and Meyer-ter-vehn1996; Qiao et al., Reference Qiao, He, Zhu and Zheng2005a). Furthermore, a sharp resonance peak is found in the interaction of a planar CP laser with a strong axial magnetic field (Liu et al., Reference Liu, He and Chen2004). To the best of our knowledge, no work has been conducted to investigate the resonant acceleration of plasma electrons in combined CP Gaussian laser fields and complete self-generated qausistatic fields so far, but it may be significant in practice. In this paper, we investigate the resonant acceleration of plasma electrons under the action of the combined laser fields and self-generated quasistatic fields. A Gaussian CP laser dependent on both space and time is introduced and the self-generated fields, including radial QSE field Es, azimuthal QSM field Bsθ, and axial QSM field Bsz are all taken into consideration. The resonant condition is analytically derived and numerically testified. The qualities of relativistic electron beam (REB) produced by resonant acceleration, including high energy, quasi-monoenergy, and small divergent angles, are discussed due to potential applications. The dependence of the final energy gain of accelerated electrons on laser intensity and plasma density is also investigated.
2. PHYSICAL MODEL AND RESONANT CONDITION
Consider a CP laser pulse with pulse duration τL and spot radius r 0 propagating through a unmagnetized underdense plasma with uniform density n 0. The CP laser electric fields with Gaussian profiles both in space and time are
where E L(r, z, t) = E 0exp{−(r 2/2r 02) − (t − (z − z 0)/v g)2/2τL2)}, φ = ωt − kz, k = ωη/c, η ≈ [1 − ωpe2/ω2 (1 + a 02)1/2]1/2, a 0 = eE 0/mωc, ωpe = 
, −e and m are electron charge and rest mass, c is the velocity of light in vacuum, v g is the laser group velocity in plasma, z 0 the initial position of the laser pulse center, and α =±1, 0 represents the circular and linear polarization, respectively. In Eqs. (1)–(3), we have ensured that ∇ · EL = 0. The magnetic field related to the laser pulse is given by ∇ × EL = −∂BL/∂t and can be formulated as follows:
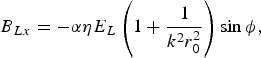
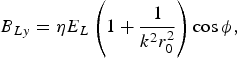
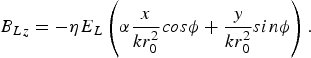
As is well-known, when an intense laser propagates in plasma, strong QSE fields, and QSM fields are self-generated by various nonlinear effects and relativistic effects (Pukhov & Meyer-ter-vehn, Reference Pukhov and Meyer-ter-vehn1996; Qiao et al., Reference Qiao, Zhu, He and Zheng2005b). These quasistatic fields will heavily affect the electron motion and acceleration. First, the ponderomotive force Fp produced by laser pulse expels some electrons away from the laser axis so that a space-charge potential Φ is formed, which corresponds to the QSE field Es = −∇Φ. The longitudinal relativistic current driven by the ponderomotive force generates the azimuthal QSM field Bsθ, while the rotational current caused by the nonlinear beat interaction of the CP laser fields with relativistic electrons produces the axial QSM field Bsz. Particle-in-cell (PIC) simulations (Zheng et al., Reference Zheng, He and Zhu2005) have shown that strong azimuthal and axial QSM fields exist in the interaction of the CP laser with dense plasma. Some of the present authors (Qiao et al., Reference Qiao, Zhu, He and Zheng2005b) have put forword a self-consistent quasistatic fields model based on the relativistic Vlasov-Maxwell equations. Introducing the normalized transform t → ωt, x → ωx/c, E → eE/m eωc, B → eB/m eωc, the model mentioned above is given by
where the coefficients k E = (1 + α2)β56I 0/r 0, k B = ε(π(1+α2)/64)n 0r 0I 0[ξβ4(T te) + (1 − ξ)β4(T re)], and b Z = (1/2)αn 0I 0[ξβ1(T te) + (1 − ξ)β1(T re)] are related to laser and plasma parameters such as n 0, I 0, etc, and among which other quantities β1, β4, β56, ξ, T te, T re, and ε are defined (Qiao et al., Reference Qiao, He, Zhu and Zheng2005a, Reference Qiao, Zhu, He and Zheng2005b).
Based on the above discussion, a test electron model is investigated. The motion of the test electron in the presence of electromagnetic fields E and B is described by the Lorentz equation
together with an energy equation
where p = γv and γ = (1 + p 2)1/2. Note that here the electric field E and magnetic field B include the laser fields EL, BL, and the self-generated quasistatic ones Es, Bs.
As pointed out (Pukhov & Meyer-ter-vehn, 1999), the electron motion in the presence of both self-generated fields Es, Bs, and laser fields EL, BL can be seen as a driven oscillation. The electron makes betatron oscillations in the self-generated electric and magnetic fields and, the laser pulse acts as a driving source. Obviously it is difficult to obtain an exact solution of Eqs. (10)–(11) because of their nonlinearity. Nevertheless, we are interested in the condition of resonance between the electron and the laser pulse. The transverse betatron oscillation of electrons can be derived by Eqs. (10)–(11). If the magnitude of transverse displacement of an electron is much smaller than the laser spot size, i.e., r 2 ≪ r 02, then E Lz and B Lz may have a negligible influence on the motion of electrons. Note the fact that the self-generated fields are slowly variant in laser-plasma interactions, it will be assumed to be static in the analytical discussion. The effect of time-dependence is included in the numerical calculations presented in Section 3. Under these assumptions, the equations governing p x and p y are
where
![\omega_b = {1\over \sqrt{\gamma}} \left[{k_E \over r_0} \left(1 - {r^2\over r_0^2}\right)+ {k_B v_z\over r_0} + {\alpha^2 b_Z^2\over \gamma} \left(1 - {2r^2\over r_0^2}\right)\right]^{1/2}\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021081903340-0408:S0263034608000086_eqn14.gif?pub-status=live)
v ph is the laser phase velocity. On the right-hand side of Eqs. (12) and (13), γ ≫ 1 is assumed and consequently the terms E L/γ, E L/γ2 are ignored in comparison with the term of E L. The derivative of longitudinal velocity v z is also neglected in the above derivation due to the slow variation of v z when the electron has been pre-accelerated. In Eq. (14), we have expanded 
. Note that ωb is the same for both the left-hand and the right-hand CP lasers and the b Z-term is absent for LP lasers. It can be seen that the electron makes betatron oscillations driven by CP laser with betatron frequency ≃ωb. When the driver frequency ω − kv z equals the betatron frequency ωb, i.e.,
![\eqalign{&{1\over \sqrt{\gamma}} \left[{k_E \over r_0} \left(1 - {r^2 \over r_0^2}\right)+ {k_B v_z\over r_0} + {\alpha^2 b_Z^2 \over \gamma} \left(1 - {2r^2\over r_0^2}\right)\right]^{1/2}\cr &\quad = 1 - {v_z\over v_{ph}}\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021081903340-0408:S0263034608000086_eqn15.gif?pub-status=live)
a resonance occurs, leading to an effective energy exchange between the pulse and electrons. In fact, after the electrons are pre-accelerated, ωb changes slowly on the time scale of one betatron oscillation. In this case, the transverse electron motion may be written
where c(t) is the magnitude of transverse momentum. Using this value of p x, p y in Eq. (11) and neglecting the rv r-term as it averages out to be zero over one oscillation period, the electron energy equation is
where ψ− = θb − (t − z/v ph) and ψ+ = θb + (t − z/v ph) are the slow ponderomotive phase and the fast ponderomotive phase, respectively. It can be seen from Eq. (17) that electrons are accelerated when their ponderomotive phase satisfies π/2 < ψ− < 3π/2, and are decelerated otherwise. The maximum acceleration is attained if the betatron oscillations are exactly in counterphase with the laser electric field. In particular, if the ponderomotive phase ψ− approximately maintains an invariable value, i.e., dψ−/dt = ωb − (1 − v z/v ph) ≃ 0, a resonance takes place. In this case, as displayed by the last term of Eq. (17), there exists a fast oscillation cos ψ+ ≃ cos 2ωbt in γ or p z for the LP lasers while it is absent in the case of CP lasers.
It can also be implied from Eq. (17) that the main accelerating term in the z-direction is −v × BL. The final energy of accelerated electrons can be approximately expressed by the combination of variation of p z and γ. Multiplying the z-product of Eq. (10) by η and subtracting from Eq. (11), we get
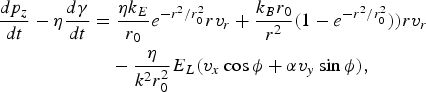
where v r = dr/dt. If the last term of the right-hand side of Eq. (18) (induced by the second terms of B Lx and B Ly) were negligible (valid for a 0 ≪ (2πr 0/λ)2), then Eq. (18) can be integrated
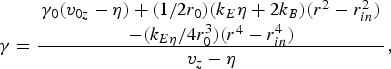
where γ0, r in and p 0z are the initial values of energy, radial coordinate, and z-directional momentum of electrons, respectively. This condition indicates that the final value of γ is a complicated function that relies not only on the initial and final longitudinal velocities, but also on the radial coordinates of the electron at the beginning and at the end of the interaction besides the rest of the plasma and laser parameters. However, the equation implies that a sudden increase in γ may happen when v z approaches v g. Furthermore, it can also be seen that if the radial QSE field and the azimuthal QSM field are absent, i.e., k E = k B = 0, then v z is always less than v g for an electron initially having v 0z < v g. This demonstrates that the electron initially located in front of the pulse center is overtaken first and then is overrun by the pulse. On the contrary, if the QSE field and the azimuthal QSM field are so large as to satisfy k Eη + 2k B > 2r 0γ0(η − v 0z)/(r 2 − r in2) (here the smaller term (k Ev g/4r 03) (r 4 − r in4) is ignored), v z will gradually approach and may surpass v g, thus the electron overtaken by the pulse first may always keep ahead of the pulse center until the end of the interaction, so gains more energy.
3. NUMERICAL ANALYSIS ON ELECTRON ACCELERATION
To further analyze the electron acceleration process, Eqs. (10)–(11) are numerically solved. We choose the parameters of laser beam as wavelength λ = 1.06 µm, the spot radius r 0 = 4λ and the pulse duration τL = 100 fs. We assume that the test electron initially locates at z = 0 while the laser pulse center is at z 0 = −4cτL. We trace the motion of electron accelerated by the laser field combined with the self-generated QSE and QSM fields. For the present self-generated fields model, we have assumed the parameters are T te = 5 KeV and ξ = 0.5 and consequently the coefficients k E, k B, and b Z can be calculated based on the definitions in Section 2. For example, if the peak laser intensity I 0 = 1 × 1020 W cm−2 and the plasma density n 0 = 0.1n cr are assumed, the peak azimuthal QSM field is about 255 megagauss (MG) near r 0; The axial QSM field gets to its peak value of 90 MG at the z axis (r = 0) and decreases as r increases; And the self-generated QSE field reaches its maximum value of 70 CGSE at r ≃ 0.7r 0.
Figure 1 shows electron trajectories in three-dimensional (3D) plane and the variation of the relative distance Δz = z − z L and of the total energy with z. The electron rotates around the direction of the laser propagation and the direction of the rotation is such that it should generate an axial magnetic field in the negative z direction by the azimuthal current. The relative distance Δz decreases first, gets to its minimum value at z ≈ 200λ. Note that the minimum distance just corresponds to v z = v g. The following increase of Δz indicates the electron has been accelerated to velocity larger than v g. A clear sharp increase in γmc 2 occurs due to the match between the electron betatron frequency ωb and the Doppler shifted laser frequency ω − kv z. That is to say, a resonance takes place. This can be explained in Figure 2, where a phase comparison of p x and B Ly is shown. One can see that an almost locked phase with ψ− ≃ π between p x and B Ly occurs from z ≈ 180λ to z ≈ 700λ, i.e., dψ−/dt ≈ 0, which indicates the resonance condition ωb ≃ ω − kv z holds. After several synchrotron rotations in the ponderomotive bucket, the phase space is mixed (about z > 700λ) and deceleration occurs. When the resonance takes place, as predicted by Eq. (17) in Section 2, the effect of polarization on the evolution of γ or p z is apparent. In the case of LP laser, the fast oscillations at 2ωb accompanying the increase of γ or p z are clearly seen in the p z plot of Figure 3b. These fast oscillations are absent for CP laser because of the rotation of the CP laser electric field. In Pukhov et al. (Reference Pukhov, Sheng and Meyer-terr-vehn1999), two-dimensional PIC simulation shows that there exists electron density modulation with two times per laser wavelength in LP laser-plasma interactions. The reason is that the transverse velocity of the resonant electrons oscillates with the laser period while the longitudinal velocity oscillating twice per laser period, leading to the electron bunching in space two times per laser wavelength. It can be seen from the resonant condition (Eq. (15)) that besides the radial QSE field Es and the azimuthal QSM field Bsθ, the axial QSM field Bsz also makes partial contribution towards betatron oscillations. Furthermore, Bsθ and Bsz play an pinch and collimation role in the acceleration process while Es partly offsets the radial ponderomotive force of the pulse.
Fig. 1. (a) Electron trajectories in three-dimensional plane and (b) the electron position relative to the pulse center and the energy gain of the electron as a function of z in the interaction of an electron with a propagating laser pulse. The parameters of laser and plasma are I 0 = 1 × 1020 W/cm2 and n 0 = 0.1n cr. The initial conditions are p x0 = p y0 = 0, γ0 = 1.01, and r in = 0. Here z L is the position of the propagating laser pulse center.
Fig. 2. Variation of p x and B Ly as a function of z for the same interaction as Fig. 1.
Fig. 3. The x- and z-momentum as a function of z in the interaction of an electron with a propagating laser pulse for different polarization. (a) CP, γ0 = 1.01 and (b) LP, γ0 = 1.5. Other parameters are the same as Fig. 1.
The continuous increase of γ leads to the decrease of ωb and the resonant condition is violated. The electron dephases and acceleration ceases. However, since the electron has been accelerated to velocity larger than v g, the laser electric field (seen by the electron) becomes more and more smaller. When the electron leaves the pulse, its energy gain still maintains a high level. It should be mentioned that the coincidence of ωb with ω − kv z just v z < v g is a determinative condition that electron attain high energy. Some electrons make betatron oscillations but dephase just v z < v g and consequently are run over by the pulse and only gain small energy.
The energetic electrons that attain resonance and have v z > v g always move ahead of the pulse and emit from the plasma channel first. The final energy gain and the scattering angles of these electrons are of our concern. The numerical calculations demonstrate that the electrons originated from the vicinity of the axis are more likely to be trapped by the ponderomotive bucket and attain high energies. The final scattering angles and spatial distribution of these energetic electrons are displayed in Figure 4, where total 180 electrons are uniformly distributed within a disc with radius r = r 0/4 placed at z = 0 initially, and their velocities approximately satisfy Maxwellian distribution with averaged temperature of 5 KeV. At the end of the interaction, we record the final energy, its radial position and its final momentum. Only electrons having energies larger than 10 MeV are shown. The scattering angle of electrons relative to the z-axis is θr = arctan(p ⊥/p ∥). In fact, we can derive 
from the equation γ2 = 1 + p ⊥2 + p ∥2. The scattering angle of the electrons obtaining γ ≫ 1 and v z > v g is doomed to be small. The numerical results show that most of the electrons attain resonance and the energy gain spreads from 207 MeV to 262 MeV with an relative energy width ΔE/〈E〉 ≃ 24%. These resonant electrons separate from the pulse with scattering angle around 3° with respect to z axis (see Fig. 4a). Moreover, the beam divergence of REB is less than 1° after the interaction is over. For comparison, The corresponding results in the case of LP laser are shown in Figure 4b. It can be seen that the REB driven by the LP laser has a larger beam divergence around 10° – 1° = 9°. The attainment of such REB is relevant to the motion of electrons. The electrons driven by the CP laser helically move within a Larmor radius induced by the axial QSM field until leaving the pulse. The spatial distribution of these electrons is almost circular (see Fig. 4c). While the motion of electrons driven by the LP pulse is about elliptical and predominantly along the direction of laser polarization (see Fig. 4d). By comparison, the REB produced by CP laser-plasma interaction with good qualities of high energy, quasi-monoenergy, and extreme low beam divergence may be a better candidate in future laser-plasma accelerator.
Fig. 4. (a) and (b) The distribution in γ − θr space, and (c) and (d) the spatial distribution of the energetic electrons in the x − y plane for different polarization when the interaction of electrons with the laser pulse is over. The total 180 electrons are initially (t = 0) located uniformly within a disc with radius r = r 0/4 placed at z = 0. Their initial velocities approximately yield Maxwellian distribution with averaged temperature 5 KeV. Here the plasma density n 0 = 0.1n cr is assumed. The peak laser intensity I 0 = 1 × 1020 W/cm2 and I 0 = 6 × 1019 W/cm2 are chosen for CP and LP, respectively.
We turn to the dependence of the energy gain of the energetic electrons on laser intensity and plasma density. The different laser intensities I 0 = 30, 60, 100 (×1018 W cm−2) and different plasma densities n 0 = 0.1n cr, 0.2n cr, 0.3n cr are chosen. The self-generated fields are correspondingly changed by Eqs. (7)–(9). Figure 5 shows that the final energy gain of accelerated electrons increases with laser intensity but decreases with plasma density. In fact, in terms of Eq. (17), the electron energy gain is proportional to the laser electric field E 0. At higher plasma density, the laser pulse travels with a lower group velocity v g and the electrons are earlier to be accelerated to reach v g and then are pushed away from the pulse. As a result, the duration of interaction between the electron and the laser pulse decreases, leading to the reduction of the energy gain.
Fig. 5. Variation of the averaged energy gain 〈γmc 2〉 over several betatron oscillations as a function of z for (a) different laser intensities, n 0 = 0.1n cr and (b) different plasma densities, I 0 = 1 × 1020 W/cm2. The initial conditions of the electron are r in = 0 and γ0 = 1.0.
A quantity that is often quoted in discussions of particle accelerators is the energy gradient, defined as the energy gained by the particle per unit of distance along its trajectory. It is usually expressed in units of MeV m−1. For example, the maximum energy gradient achievable in radio-frequency (rf) conventional accelerators is 100 MeV m−1. In our case, the energy gain in general is about tens or hundreds of MeV with acceleration length around several millimeters. So we can attain the energy gradient about tens or hundreds of GeV m−1, which is 2~3 orders larger than the rf accelerators.
4. CONCLUSION
In conclusion, the resonance acceleration of plasma electrons in interaction of an intense short laser with underdense plasma is theoretically and numerically studied by using a test particle model, where the joint effect of the CP Gaussian laser fields and the self-generated quasistatic fields, including the radial QSE field, the azimuthal QSM field, and the axial QSM field, is included. It is found that the resonance takes place when the betatron oscillation frequency of electrons in self-generated quasistatic fields coincides with the Doppler shifted laser frequency. Due to resonant acceleration, some electrons attain energy directly from the laser pulse and thus form a well qualified REB with high energy, quasi-monoenergy and extreme low divergent angle. It is also found that the final energy of the REB increases with laser intensity but decreases with plasma density. Our results show that the REB produced by CP laser-plasma interaction has better collimation comparing to the LP case for the resonant electrons move helically within a Larmor radius induced by the axial QSM field. We believe that our results can give some enlightenment on the future laser-plasma based accelerators.
Acknowledgments
We acknowledge helpful discussions with H. B. Cai on this work. This work is supported by the National Natural Science Foundation of China, Grant Nos. 10576007, 10335020, and 10575013, and the National High-Tech ICF Committee in China, and partially by the National Basic Research Program of China (973) (2007CB814802 and 2007CB815101).
