Introduction
The interaction of intense laser pulses with plasmas has been studied extensively these days due to its rapidly growing interest in understanding a number of non-linear physical processes arising from the laser–plasma interactions. These processes are finite pulse effect, filamentation, self-phase modulation, second harmonic generation (Kant et al., Reference Kant, Gupta and Suk2011), and self-focusing of laser/electromagnetic waves. The study of some of these physical process leads to the insight of laser–plasma interaction dynamics, keeping non-linear process at a low level. Much attention has been given to the study of self-focusing these days, due to its wide range of applications, such as inertial confinement fusion (ICF) (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth and Mason1994; Regan et al., Reference Regan, Bradley, Chirokikh, Craxton, Meyerhofer, Seka and Drake1999), ionospheric modification (Guzdar et al., Reference Guzdar, Chaturvedi, Papadopoulos and Ossakow1998; Gondarenko, Reference Gondarenko2005), and new radiation sources (Fedotov et al., Reference Fedotov, Naumov, Silin, Uryupin and Zheltikov2000). The success of these applications depends on the possibility of long distance propagation of intense laser beam in plasmas. The laser beam tends to diverge naturally due to diffraction effects, which is counterbalanced by the self-focusing of the laser beam led by nonlinear behavior of the medium. However, in the absence of nonlinearity, the beam will diverge appreciably in a Rayleigh length.
With the availability of intense laser pulses, relativistic self-focusing results due to the quiver motion of electrons. The oscillatory electron velocity reaches comparable to the velocity of light leading to reduced local plasma frequency. Another non-linear phenomena arises due to ponderomotive force-type non-linearity resulting in radiation pressure (Hora, Reference Hora1969). Because of the immense pressure, the electrons are expelled from high field intensity to the lower field intensity region. This results in the modification of the density distribution of electrons in plasma, thereby developing density gradient. The combined effect of both (relativistic and ponderomotive) non-linearities thus affects the beam propagation and is well established both theoretically and experimentally by various researchers. These contributions are thus represented with a third-order non-linearity in the weakly relativistic limit in laser wave equation (Patil et al., Reference Patil, Takale, Fulari, Gupta and Suk2013). In a weakly relativistic ponderomotive (RP) plasma medium, the assumption τ ≫ τpe >T 0 is valid, where τ is the laser pulse duration, τpe is the electron response time, and T 0 is the laser period. Since the ions are relatively heavier than electrons, the force acting on ion is neglected in the present investigation.
The above model for weakly relativistic ponderomotive regime has been studied extensively recently by various researchers using fundamental TEM00 mode Gaussian laser beam. Niknam et al. (Reference Niknam, Milani, Bokaeia and Hashemzadeha2013) has recently studied the electron density distribution due to the effect of weakly relativistic ponderomotive force in the interaction of laser pulses with plasma. Patil et al. (Reference Patil, Takale, Navare, Fulari and Dongare2012) have studied the effect of weakly relativistic and ponderomotive self-focusing by choosing the appropriate experimental parameters and for laser power greater than critical power. They observed that the inclusion of ponderomotive term in relativistic term enhances beam focusing.
Self-focusing due to the combined effect of relativistic and ponderomotive non-linearities and its effect on modulation instability arising due to density perturbation have been studied by Jha et al. (Reference Jha, Malviya, Upadhyay and Singh2008). Further, density steepening occurring because of plasma inhomogeneity and plasma permittivity due to weakly relativistic and ponderomotive profile is studied by Niknam et al. in collisionless and collisional regimes (Niknam et al., Reference Niknam, Hashemzadeh and Shokri2009). They have further derived modified dielectric constant for cold under dense plasma and investigate the profile of electric and magnetic field. The deviation of electromagnetic field profile from sinusoidal behavior is observed. Apart from taking Gaussian laser beam, a few studies have been attempted by considering non-Gaussian laser beams. In such an endeavor, Patil and Takale (Reference Patil and Takale2013b) have studied self-focusing of cosh-Gaussian (ChG) beams in plasma by taking weakly RP regime. The results obtained by them were in reasonable agreement with variational approach followed by Gill et al. (Reference Gill, Mahajan and Kaur2011) and stronger self-focusing is observed in comparison with relativistic case. Kumar et al. (Reference Kumar, Aggarwal, Richa and Gill2016) have recently revisited the Patil et al.’s (Reference Patil, Takale, Fulari, Gupta and Suk2013) work by considering pinching effect of quantum plasma and by taking combined effect of both ponderomotive and relativistic non-linearity. The model established was successful in explaining the role of ponderomotive non-linearity in enhancing the beam focusing when the density of the plasma electrons becomes sufficiently very high.
Being a newly emerging field in plasma physics, quantum plasmas have gained increasing attention during the past few years (Ren et al., Reference Ren, Wu and Chu2007; Jung and Murakami, Reference Jung and Murakami2009; Hefferon et al., Reference Hefferon, Sharma and Kourakis2010; Shukla and Eliassion, Reference Shukla and Eliassion2010). When the density of plasma electrons becomes very high, quantum effects start playing a vital role. Many investigations have been reported recently on the plasma systems where quantum effects are dominant and have relevance in a variety of applications viz cosmological and astrophysical systems (Jung, Reference Jung2001; Opher et al., Reference Opher, Silva, Dauger, Decyk, Dawson, Opher and Dawson2001), laser-produced plasmas (Kremp et al., Reference Kremp, Bonitz and Schlanges1999), laser–solid plasma interactions (Kremp et al., Reference Kremp, Bonitz and Schlanges1999; Marklund and Shukla, Reference Marklund and Shukla2006), etc. In almost all these applications, quantum effects are dominant due to high-density plasmas. The tendency of quantum plasma as a non-linear medium (Patil and Takale, Reference Patil and Takale2013a, Reference Patil and Takale2014; Habibi and Ghamari, Reference Habibi and Ghamari2014; Kumar et al., Reference Kumar, Aggarwal, Richa and Gill2016; Aggarwal et al., Reference Aggarwal, Kumar and Gill2017) has grown interest in all the practical situations, where de Broglie wavelength of charged particles is greater than or equal to the inter particle distance, therefore one cannot ignore the quantum nature of the plasma constituents.
However, in recent years, a number of theoretical investigations have been ventured by studying self-focusing of the laser beam in plasma considering Gaussian (Zhou et al., Reference Zhou, Wang, Yuan and Du2011; Navare et al., Reference Navare, Takale, Patil, Fulari and Dongare2012; Patil and Takale, Reference Patil and Takale2013b, Reference Patil and Takale2014; Aggarwal et al., Reference Aggarwal, Kumar and Kant2016), cosh Gaussian (Patil et al., Reference Patil, Navare, Takale and Dongare2009; Gill et al., Reference Gill, Mahajan and Kaur2011; Patil et al., Reference Patil, Takale, Navare, Fulari and Dongare2012; Aggarwal et al., Reference Aggarwal, Vij and Kant2014), Hermite Cosh Gaussian (Patil et al., Reference Patil, Takale and Navare2010; Nanda et al., Reference Nanda, Kant and Wani2013; Kant and Nanda, Reference Kant and Nanda2014; Nanda and Kant, Reference Nanda and Kant2014; Wani and Kant, Reference Wani and Kant2016; Wani et al., Reference Wani, Ghotra and Kant2018), elliptical Gaussian laser beam (Nayyar and Soni, Reference Nayyar and Soni1978; Soni and Nayyar, Reference Soni and Nayyar1980; Singh et al., Reference Singh, Aggarwal and Gill2008; Singh and Walia, Reference Singh and Walia2012), and multiple Gaussian laser beam (Sati et al., Reference Sati, Sharma and Tripathi2012). In many applications, high-power densities at the target are required. So in an attempt to achieve it, there is the common practice of combining multiple laser beams. Mutual focusing/defocusing and cross-focusing of two laser beams have been studied by many coworkers in the past few years. However, combining four beams identically are mathematically easier than combining two beams. Self-focusing of the quadruple Gaussian laser beam comprising four coherent Gaussian laser beams has already been studied considering ponderomotive non-linearity (Sati et al., Reference Sati, Sharma and Tripathi2012). Aggarwal et al. (Reference Aggarwal, Vij and Kant2015a; Reference Aggarwal, Vij and Kant2015b) extended the above work and studied self-focusing of circularly polarized quadruple Gaussian laser beam in relativistic magnetized plasma. In their investigation, enhanced self-focusing is reported when laser beam propagates in extraordinary mode rather than in ordinary mode. In a similar investigation, self-focusing of the quadruple Gaussian laser beam is thoroughly studied in inhomogeneous magnetized plasma by considering linear absorption (Aggarwal et al., Reference Aggarwal, Vij and Kant2015a, Reference Aggarwal, Vij and Kant2015b). Their observation shows that, the initial converging/diverging beam shows oscillatory convergence and divergence, respectively, and the beam is more focused at lower intensity rather than at higher intensities. However, no attempt had been made by researchers to enhance the self-focusing of the quadruple Gaussian beam using relativistic and ponderomotive regime in the presence of cold quantum plasma.
The paper is modeled as follow: In “Formalism” section, authors have developed the non-linear part of plasma permittivity by taking into account weakly RP non-linearity and by inclusion of cold quantum plasma. In “Self-focusing” section , authors have set up the non linear differential equation governing the propagation of quadruple Gaussian beam. Results are presented in “Numerical results and discussion” section.
Formalism
Consider quadruple Gaussian laser beam with angular frequency “ω” propagating in unmagnetized cold quantum plasma along the z direction in cylindrical coordinate system. The magnitude of electric field vector “
${\bf E}$” of laser beam is given as
$${\bf E} = \hat xA(x,y,z)\exp [i({\rm \omega} t - kz)],$$
where A is the amplitude of the laser field, 
$k = {\rm \omega} \sqrt {{\rm \epsilon} _{\rm o}} /c$ is the wave propagation constant, εo is the dielectric constant of the medium on the axis, and c is the speed of light in free space.
The initial intensity distribution of the quadruple laser beam is given by (Sati et al., Reference Sati, Sharma and Tripathi2012):
$$\eqalign{AA^{\rm \star} \vert _{z = 0} = & \,(16)^2A_{{\rm oo}}^2 [e^{ - ((x - x_{\rm o})^2 + y^2)/2r_{\rm o}^{\rm 2}} + e^{ - ((x + x_{\rm o})^2 + y^2)/2r_{\rm o}^2} \cr & + e^{ - (x^2 + {(y - x_{\rm o})}^2)/2r_{\rm o}^2} + e^{ - (x^2 + {(y + x_{\rm o})}^2)/2r_{\rm o}^{\rm 2}} ]^2,} $$where (−x o, 0), (x o, 0), (0, −x o), and (0, x o) are the amplitude maxima of four identical coherent Gaussian beams comprising the quadruple beam. The intensity distribution of quadruple Gaussian beam for z > 0 in the paraxial ray approximation can be written in the following form:
$$\eqalign{AA^{\rm \star} = & \,\displaystyle{{{(16)}^2A_{{\rm oo}}^2} \over {\,f^2}}[e^{ - ((x - x_{\rm o}f)^2 + y^2)/2f^2r_{\rm o}^2} + e^{ - ((x + x_{\rm o}f)^2 + y^2)/2f^2r_{\rm o}^{\rm 2}} \cr & + e^{ - (x^2 + {(y - x_{\rm o}f)}^2)/2f^2r_{\rm o}^{\rm 2}} + e^{ - (x^2 + {(y + x_{\rm o}f)}^2)/2f^2r_{\rm o}^{\rm 2}} ]^2,} $$
where 
$16A_{{\rm oo}}e^{ - x_{\rm o}^2 /2r_{\rm o}^2} $ is the laser amplitude and r o is the initial half width of each beam segment wave.
The effective dielectric permittivity ε for cold quantum plasma is of the following form (Jung and Murkami, Reference Jung and Murakami2009):
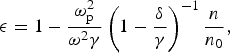$${\rm \epsilon} = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} ^2{\rm \gamma}}} \left( {1 - \displaystyle{{\rm \delta} \over {\rm \gamma}}} \right)^{ - 1}{n \over n_0},$$where γ = (1 + α|A|2)1/2 is the relativistic factor with α = e 2/m 2c 2ω2. Here, e and m are the electronic charge and rest mass, respectively. δ = 4π4h 2/m 2ω2λ4 is a parameter which is associated with quantum wavelength of the species (λ) and, h is the planck constant. ωp = (4πne 2/m)1/2 is the plasma frequency and n is the electron density, which is modified by ponderomotive force in the steady state and is given by (Niknam et al., Reference Niknam, Hashemzadeh and Shokri2009):
$$n = n_0\exp \left( { - \displaystyle{{mc^2} \over {T_{\rm e}}}({\rm \gamma} - 1)} \right).$$
Here, T e is the electron temperature in units of energy and n 0 is the maximum electron density where the laser electric field is zero. In Eq. (4), ε is a function of irradiance 
${\bf E}{\bf E}^{\rm \star} $ of quadruple Gaussian beam, which is a function of r 2. In paraxial ray approximation, ε can be Taylor expanded in the radial direction around r = 0 as
$${\rm \epsilon} (r) = {\rm \epsilon} _{\rm o} - \displaystyle{{r^2} \over {r_{\rm o}^2}} \Phi, $$where
$${\rm \epsilon} _{\rm o} = 1 - \displaystyle{{{\rm \omega} _{{\rm po}}^2} \over {{\rm \omega} ^2{\rm \gamma} _{\rm o}}}\left( {1 - \displaystyle{{\rm \delta} \over {{\rm \gamma} _{\rm o}}}} \right)^{ - 1}\exp \left( { - \displaystyle{{mc^2} \over {T_{\rm e}}}({\rm \gamma} _{\rm o} - 1)} \right),$$and
$$\eqalign{ {\rm \phi} = & \displaystyle{{{\rm \omega} _{{\rm po}}^2} \over {(2{\rm \omega} ^2)}}\displaystyle{1 \over {\,f^3{\rm \gamma} _0^3}} \left( {\displaystyle{X \over f}} \right)\left( { - 1 + \displaystyle{{x_{\rm o}^{\rm 2}} \over {2r_{\rm o}^{\rm 2}}}} \right)\left( {1 - \displaystyle{{\rm \delta} \over {{\rm \gamma} _{\rm o}}}} \right)^{ - 2} \cr & \times \left[ {1 + \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}\left( {{\rm \gamma} _{\rm o} - {\rm \delta}} \right)} \right]{\rm exp}\left[ { - \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}\left( {{\rm \gamma} _{\rm o} - 1} \right)} \right],} $$
where ωpo = (4πn oe 2/m)1/2, γo = (1 + X)1/2, and 
$X = (16^2{\rm \alpha} A_{{\rm oo}}^2 e^{( - x_{\rm o}^2 )/(r_{\rm o}^{\rm 2} )}/f^2).$
Self-focusing
The general form of non-linear wave equation governing the evolution of the electric field is obtained as
$$\displaystyle{{\partial ^2E} \over {\partial z^2}} + \left( {\displaystyle{{\partial ^2} \over {\partial x^2}} + \displaystyle{{\partial ^2} \over {\partial y^2}}} \right)E + \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \epsilon} E = 0.$$
The above equation can be obtained in the light of Maxwell's equations. The inequality 
$k^{ - 2}\nabla ^2({\rm ln}{\rm \epsilon} ) \ll 1$ is valid in almost all situations of practical interest. One can obtain quasioptic equation by putting E from Eq. (1) in Eq. (9), and using Wentzel–Krammers–Brillouin approximation. By neglecting 
$\partial ^2{\bf A}/\partial z^2$ the resulting wave equation reduces to:
$$ - \!2ik\displaystyle{{\partial A} \over {\partial z}} + \left( {\displaystyle{{\partial ^2A} \over {\partial x^2}} + \displaystyle{{\partial ^2A} \over {\partial y^2}}} \right) - \displaystyle{{r^2} \over {r_0^2}} \displaystyle{{{\rm \omega} ^2} \over {c^2}}{\rm \phi} A = 0.$$We follow an approach given by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and further developed by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976). Hence introducing an eikonal as A = A o(r, z)exp[−ikS(r, z)] in Eq. (10) and separating real and imaginary parts, one can obtain:
$$ \hskip+-5pt 2\displaystyle{{\partial S} \over {\partial z}} + \! \left[ {{\left( {\displaystyle{{\partial S} \over {\partial x}}} \right)}^2 + {\left( {\displaystyle{{\partial S} \over {\partial y}}} \right)}^2} \right] \!= \!\left( {\displaystyle{{\partial ^2A_{\rm o}} \over {\partial x^2}} + \displaystyle{{\partial ^2A_{\rm o}} \over {\partial y^2}}} \right)\displaystyle{1 \over {k^2A_{\rm o}}} + \displaystyle{{r^2} \over {r_0^2}} \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} ^2}}\displaystyle{{\rm \phi} \over {{\rm \epsilon} _{\rm o}}},$$
$$\displaystyle{{\partial A_{\rm o}^2} \over {\partial z}} + \left[ {\displaystyle{{\partial A_{\rm o}^2} \over {\partial x}}\displaystyle{{\partial S} \over {\partial x}} + \displaystyle{{\partial A_{\rm o}^2} \over {\partial y}}\displaystyle{{\partial S} \over {\partial y}}} \right] + A_{\rm o}^2 \left[ {\displaystyle{{\partial ^2S} \over {\partial x^2}} + \displaystyle{{\partial ^2S} \over {\partial y^2}}} \right] = 0.$$Here, A o(r, z) and S(r, z) are real functions of space variables. The solution of Eqs (11) and (12) can be written as
$$A_{\rm o}^2 = \displaystyle{{{(16)}^2A_{{\rm oo}}^{\rm 2}} \over {\,f^2}}e^{ - x_{\rm o}^{\rm 2} /r_{\rm o}^{\rm 2}} e^{ - r^2/f^2r_{\rm o}^{\rm 2}} \left( {1 + \displaystyle{{r^2x_{\rm o}^2} \over {4r_{\rm o}^4 f^2}} + \displaystyle{{(x^4 + y^4)x_{\rm o}^4} \over {48r_{\rm o}^8 f^4}}} \right)^2,$$and
$$S = S_{\rm o} + \displaystyle{1 \over f}\displaystyle{{df} \over {dz}}\left( {\displaystyle{{x^2} \over 2} + \displaystyle{{y^2} \over 2}} \right).$$Differentiating Eq. (14) w.r.t. x, y, z and substituting in Eq. (11), we get
$$2\displaystyle{{\partial S_{\rm o}} \over {\partial z}} + \displaystyle{{r^2} \over f}\displaystyle{{d^2f} \over {dz^2}} = \left( {\displaystyle{{\partial ^2A_{\rm o}} \over {\partial x^2}} + \displaystyle{{\partial ^2A_{\rm o}} \over {\partial y^2}}} \right)\displaystyle{1 \over {k^2A_{\rm o}}} + \displaystyle{{r^2} \over {r_0^2}} \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} ^2}}\displaystyle{{\rm \phi} \over {{\rm \epsilon} _{\rm o}}},$$where
$$\left( {\displaystyle{{\partial ^2A_{\rm o}} \over {\partial x^2}} + \displaystyle{{\partial ^2A_{\rm o}} \over {\partial y^2}}} \right)\displaystyle{1 \over {A_{\rm o}}} = \displaystyle{{ - 2} \over {r_{\rm o}^2 f^2}}\left( {1 - \displaystyle{{x_{\rm o}^2} \over {2r_{\rm o}^2}}} \right) + \displaystyle{{r^2} \over {r_{\rm o}^4 f^4}}\left( {1 - \displaystyle{{x_{\rm o}^2} \over {r_{\rm o}^2}}} \right).$$By substituting Eqs (8) and (13) in Eq. (15) and equating the coefficient of r 2 on both sides, one can obtain the equation of self-focusing of quadruple Gaussian beam in relativistic and ponderomotive regime as given below:
$$\eqalign{\displaystyle{{d^2f} \over {d{\rm \zeta} ^2}} & = \displaystyle{1 \over {\,f^3}}\left( {1 - \displaystyle{{x_{\rm o}^2} \over {r_{\rm o}^2}}} \right) - \displaystyle{1 \over 2}\left( {\displaystyle{{{\rm \omega} _{\rm p}r_0} \over c}} \right)^2\displaystyle{1 \over {\,f^2{\rm \gamma} _0^3}} \left( {\displaystyle{X \over f}} \right) \cr & \quad \times \left( { - 1 + \displaystyle{{x_{\rm o}^2} \over {2r_{\rm o}^2}}} \right)\left( {1 - \displaystyle{{\rm \delta} \over {{\rm \gamma} _{\rm o}}}} \right)^{ - 2}\left[ {1 + \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}\left( {{\rm \gamma} _{\rm o} - {\rm \delta}} \right)} \right] \cr & \quad \times {\rm exp}\left[ { - \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}\left( {{\rm \gamma} _{\rm o} - 1} \right)} \right].} $$
Here 
${\rm \zeta} = z/kr_{\rm o}^2 $ is dimensionless distance of propagation. On r.h.s of Eq. (17), the first term (diffraction term) responsible for diffractional divergence of the beam and the second term (nonlinear term), leads to the relativistic and ponderomotive self-focusing determining the propagation character of the beam. Equation (17) is solved using suitable laser and plasma parameters and for an initial plane wave front i.e. for (df/dζ) = 0 and f = 1 at ζ = 0. The propagation characteristic of quadruple Gaussian beam could be determined without convergence or divergence for the condition (d 2f/dζ2) = 0, i.e., in the self-trapped mode. Using (d 2f/dζ2) = 0, in Eq. (17), one can obtain a relation between inverse of square of equilibrium beam radius ρo = r oωp/c and critical intensity of the beam 
$\Pi _{\rm o}^2 = {\rm \alpha} A_{{\rm oo}}^{\rm 2} $. The expression after simplification can be written as:
$$\displaystyle{1 \over {{\rm \rho} _{\rm o}^2}} = \displaystyle{\matrix{X_1\left( {1 + X_1} \right)^{ - 3/2}\left( { - 1 + \displaystyle{{x_{\rm o}^2} \over {2r_{\rm o}^2}}} \right)\left[ {1 + \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}{(1 + X_1)}^{ -\textstyle { 1 \over 2}} - {\rm \delta}} \right] \hfill \cr \quad \exp \left[ { - \displaystyle{{m_{\rm o}c^2} \over {T_{\rm e}}}\left( {{\left( {1 + X_1} \right)}^{\textstyle{1 \over 2}} - 1} \right)} \right]\left( {1 - {\rm \delta} {\left( {1 + X_1} \right)}^{- \textstyle{{ 1} \over 2}}} \right)^{ - 2} \hfill} \over {2\left( {1 - \displaystyle{{x_{\rm o}^2} \over {2r_{\rm o}^2}}} \right)}}.$$
Here, 
$X_1 = 256{\rm \alpha} A_{{\rm oo}}^{\rm 2} e^{( - x_{\rm o}^2 )/(r_{\rm o}^2 )}.$
Numerical results and discussion
In the present section, we will discuss the self-focusing of quadruple Gaussian laser beam in cold quantum plasma. Equation (17) is the fundamental second-order non-linear differential equation governing the beam width parameter as a function of normalized distance of propagation ζ. The analytical solution of Eq. (17) is not possible; therefore, we seek the help of numerical computation to investigate the evolution of beam dynamics. There are several terms on the r.h.s of Eq. (17) and the fate of the laser beam depends on various parameters such as lateral separation (x 0/r 0), electron temperature (T e), cold quantum parameter (δ), and relativistic factor (γ). All these parameters play a vital role in contributing to the dynamics of the laser beam for the following set of parameters chosen: ωo = 1.778 × 1020rad/s, r o = 0.001 cm, λ = 0.0106 nm, n o = 1.0 × 1019/cm3, intensity = 5.45 × 1026W/cm2, ωc/ωo = 0.1−0.5, and T e = 15 KeV.
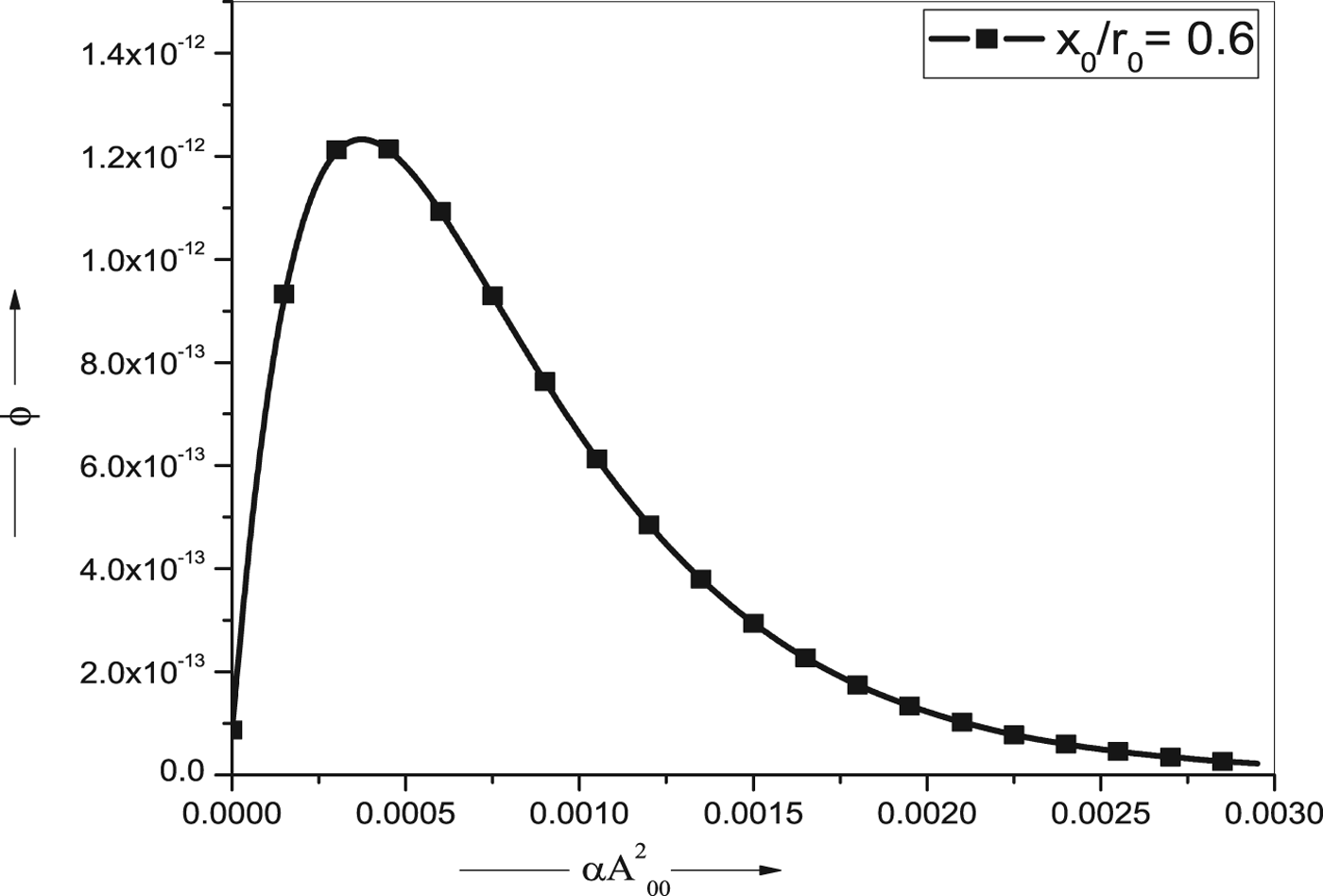
Figure 1 depicts the graph for the variation of non-linear plasma permittivity ϕ as a function of intensity and for fixed value of lateral separation parameter (x 0/r 0 = 0.6). The non-linearity is an increasing function of intensity up to intensity = 5.45 × 1026 W/cm2 thereby leading to reduced focusing length of the beam. The plasma permittivity is found to fall rapidly after achieving maximum. Since plasma permittivity is also a function of temperature, so we have elaborated our results and plotted the variation of plasma permittivity ϕ as a function of electron temperature.
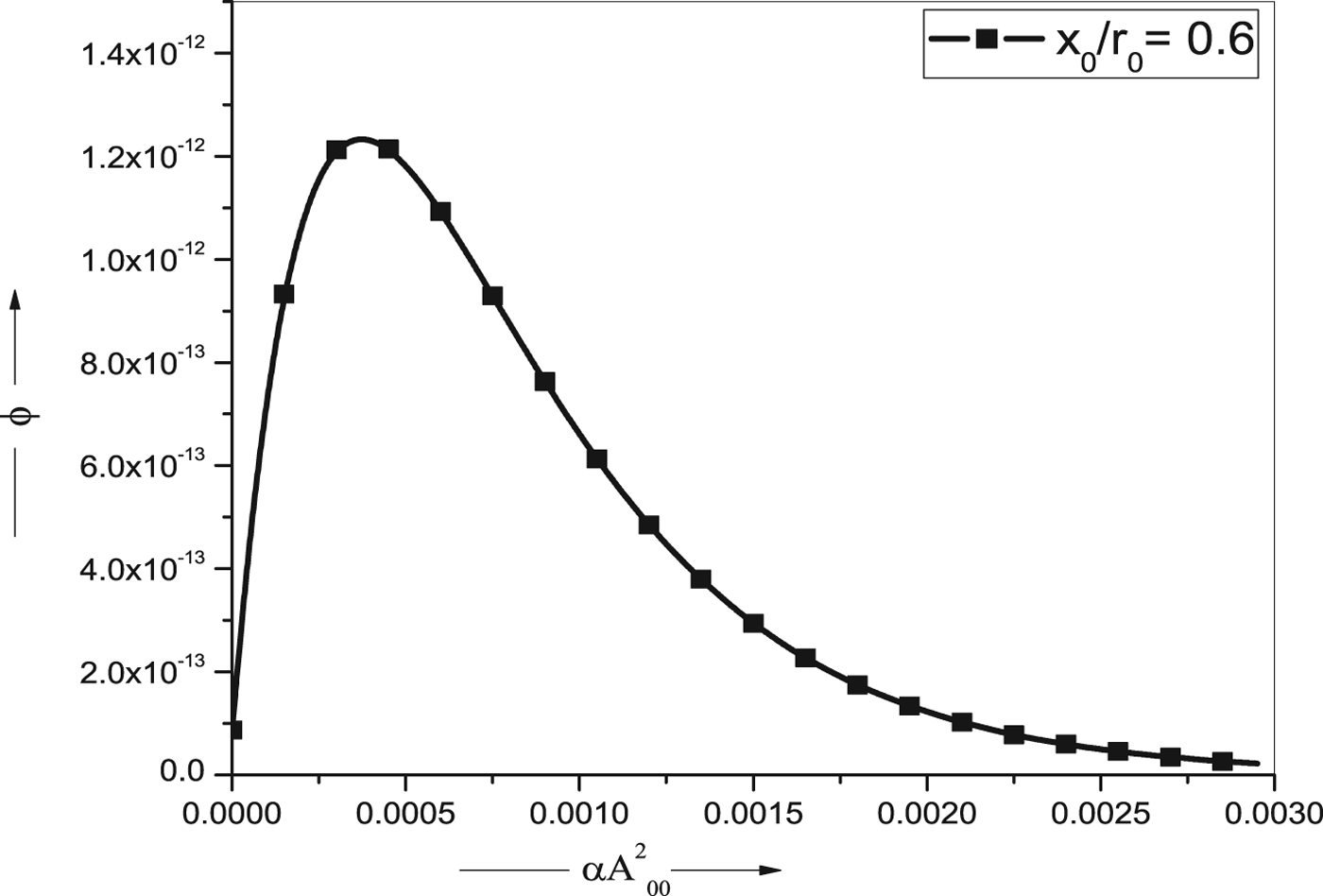
Fig. 1. Variation of non-linear plasma permittivity ϕ with intensity parameter in case of RPCQ plasma for x 0/r 0 = 0.6 and other parameters are as follow: r 0 = 0.001 cm, λ = 0.0106 nm, n o = 1.0 × 1019/cm3, and T e = 15 KeV.
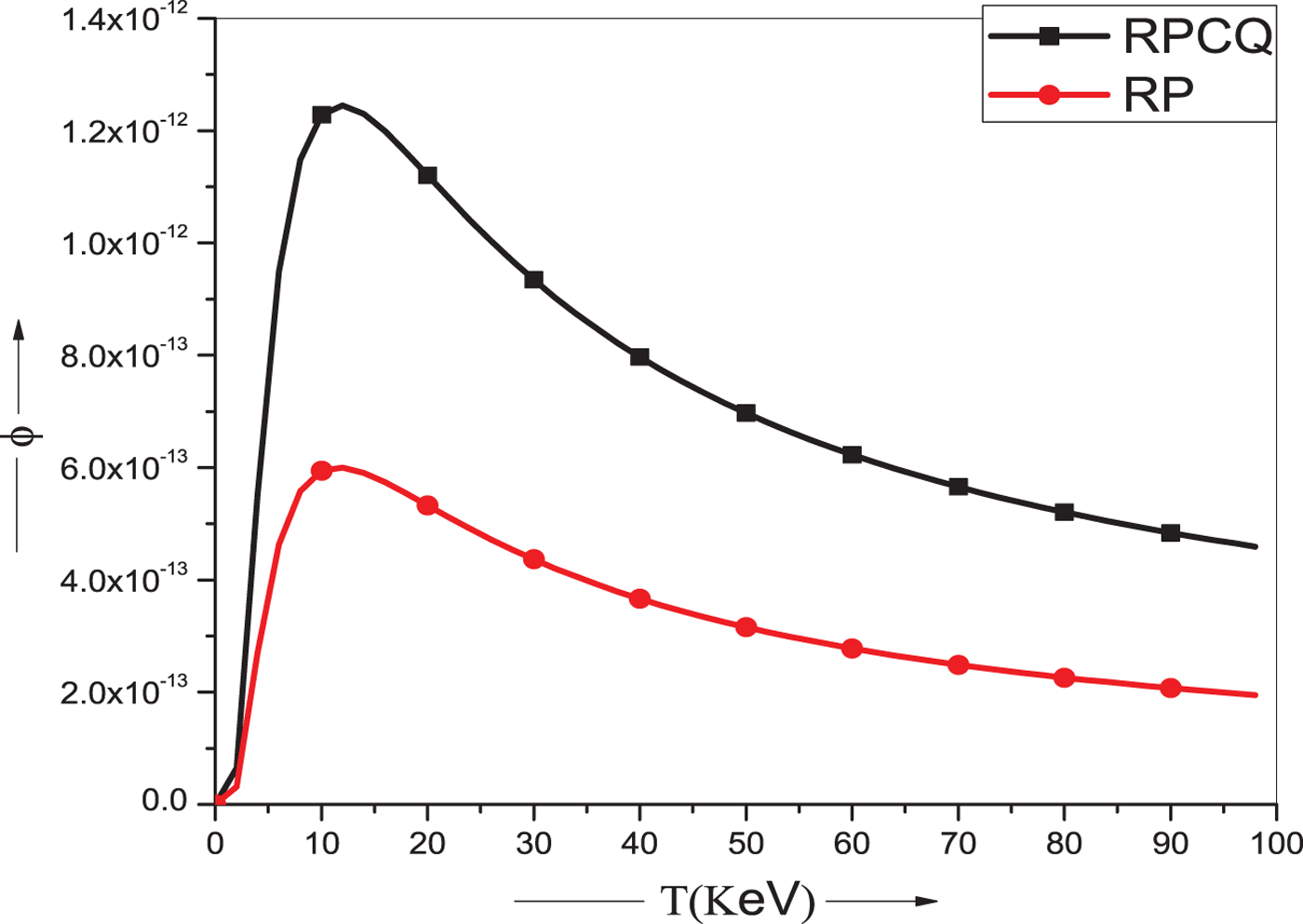
Figure 2 represents the variation of non-linear plasma permittivity ϕ as a function of electron temperature. It is clear from the graph that the non-linearity in case of relativistic ponderomotive cold quantum plasma (RPCQ) is stronger than RP plasma as the non-linearity saturates more for RPCQ than RP case of reference. This is due to the fact that the effect of ponderomotive non-linearity assists the relativistic effects and results in stronger self-focusing. The electron temperature for which maxima is attained in case of RPCQ is 15 KeV. Therefore, strongest self-focusing is achieved at T e = 15 KeV as elucidated from Figure 5. The electron temperature is optimized to ensure stronger self-focusing as the laser propagation takes place in denser plasmas.
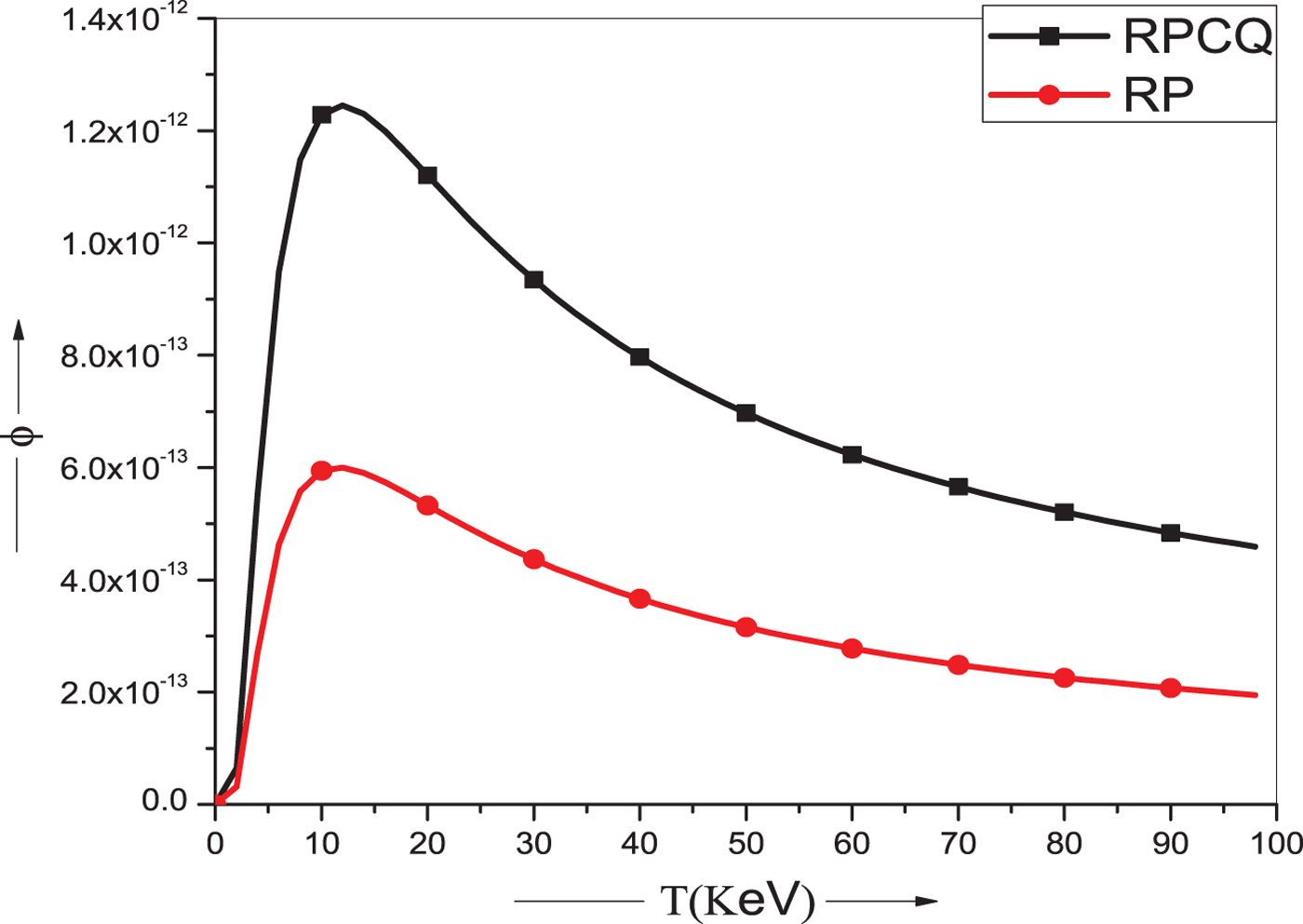
Fig. 2. Variation of non-linear plasma permittivity ϕ with electron temperature for two types of plasma model RPCQ and RP and for x 0/r 0 = 0.6. The other parameters being same as mentioned in caption of Figure 1.
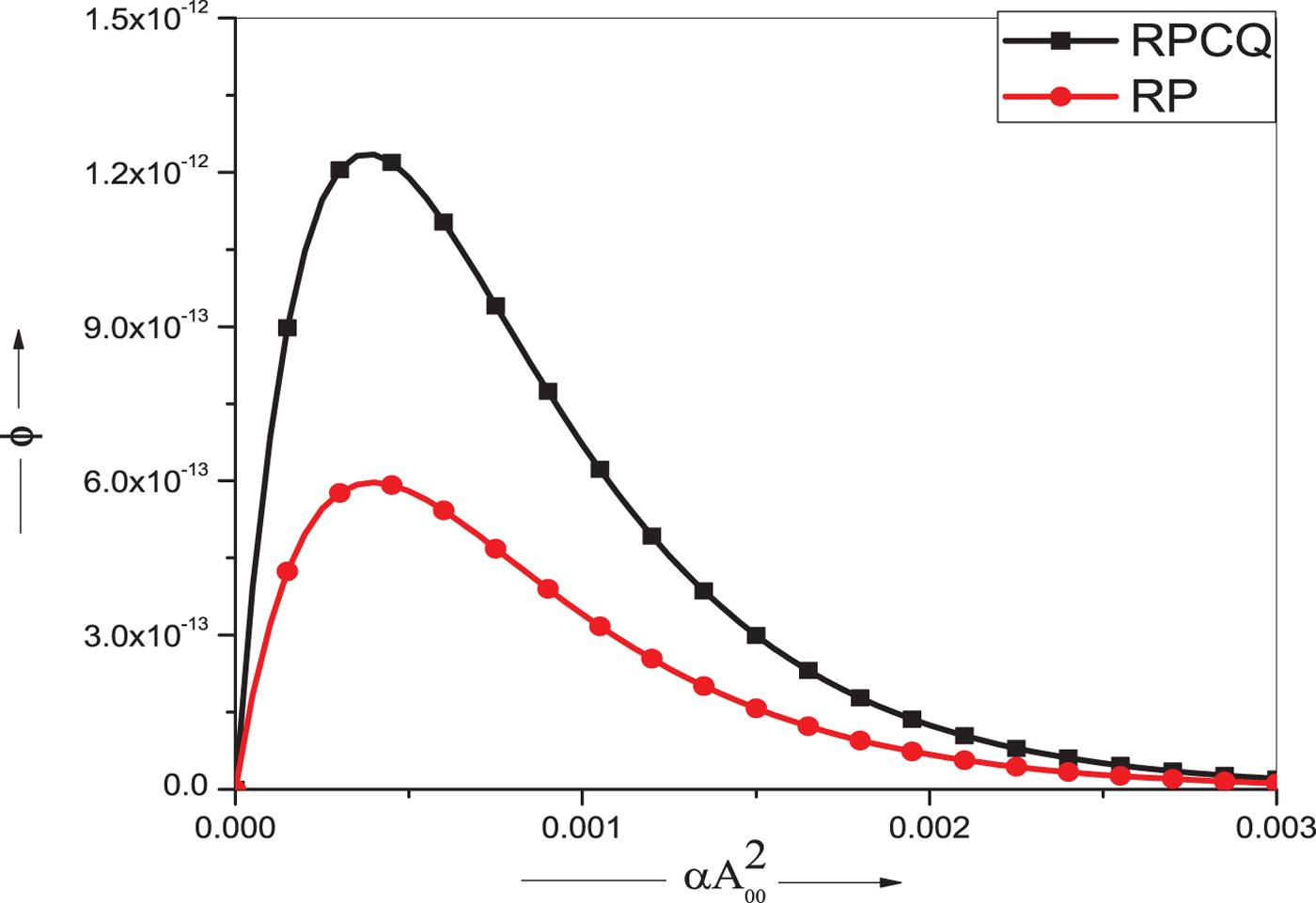
Fig. 3. Variation of nonlinear plasma permittivity ϕ with intensity parameter for two types of plasma model RPCQ and RP for x 0/r 0 = 0.6. The other parameters being same as mentioned in caption of Figure 1.
Figure 3 depicts the variation of plasma permittivity ϕ as a function of intensity in case of RPCQ and RP plasma for fixed value of lateral separation parameter (x 0/r 0 = 0.6). The plasma permittivity increases with intensity and achieves maximum and thereafter it falls rapidly. The behavior is similar in both cases of RPCQ and RP plasma models. The maximum achieved in case of RPCQ is appreciably larger than RP plasma model for the same set of laser and plasma parameter chosen. Thus, there is a wide range of laser intensities that can be focused in case of RPCQ plasma in comparison with RP plasma.
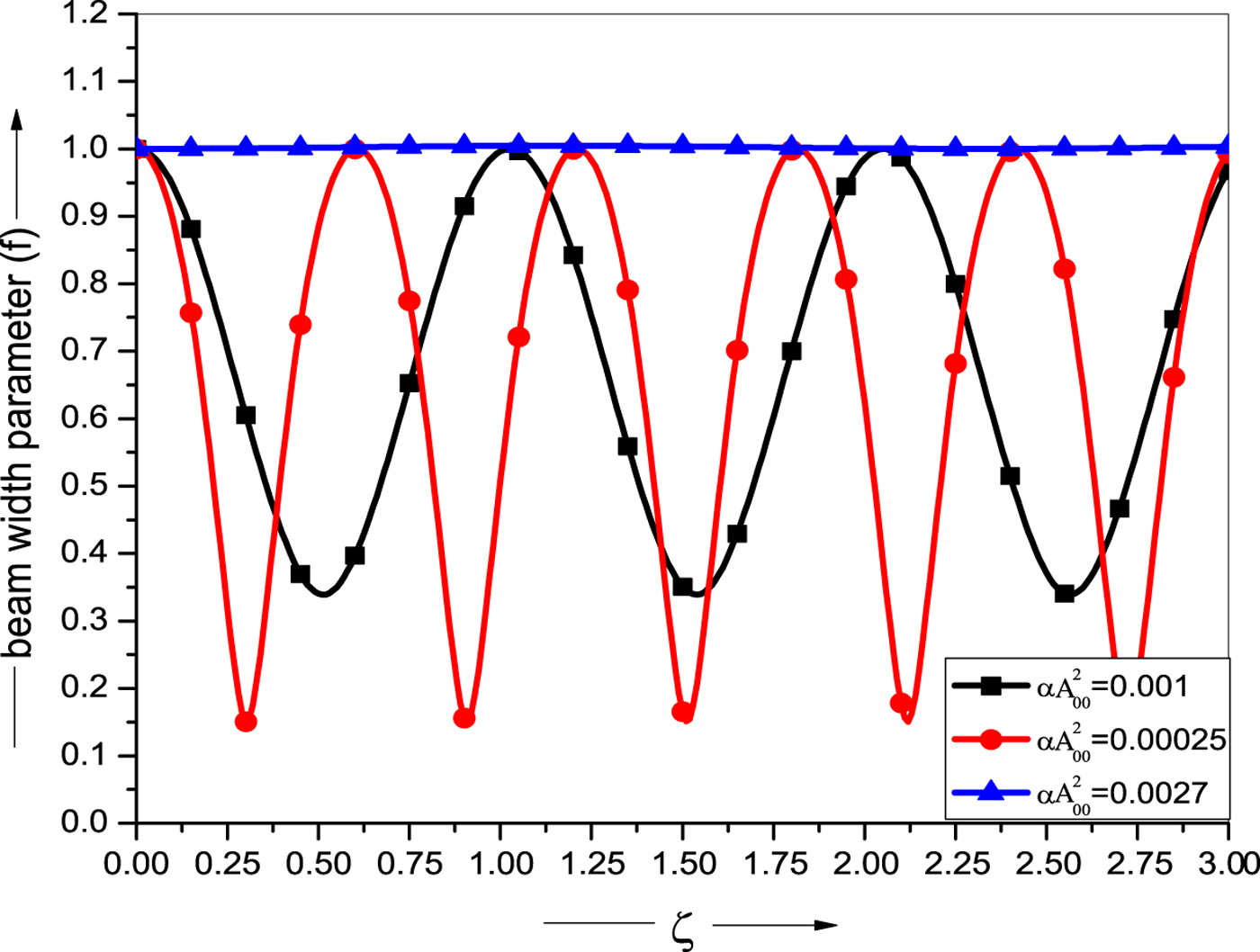
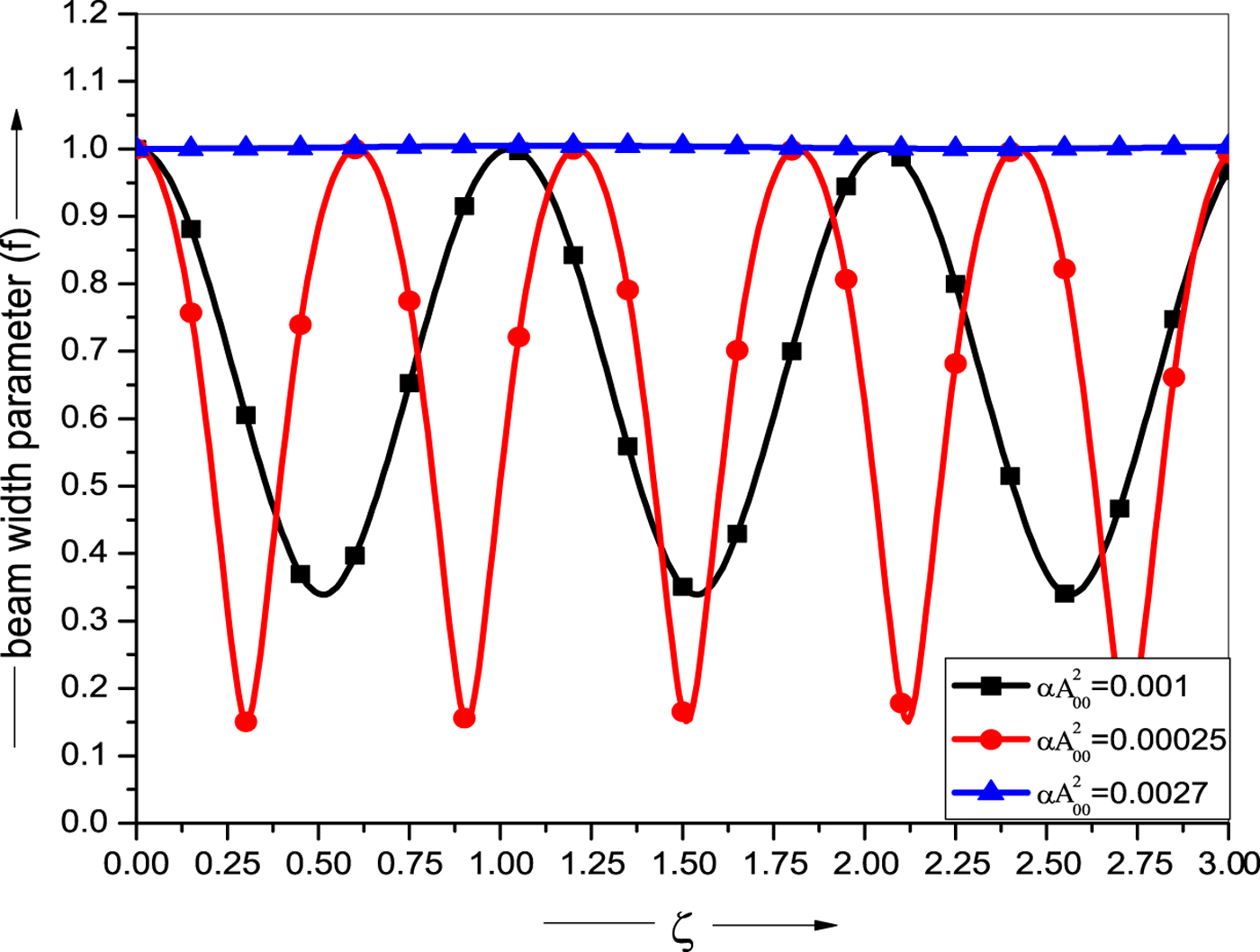
Fig. 4. Variation of beam width parameter f with normalized propagation distance ζ for relativistic ponderomotive cold quantum plasma (RPCQ) for different values of intensity parameter αA 200 = 0.001, 0.00025, 0.0027. The other parameters are same as in Figure 1.
Figure 4 depicts the variation of beam width parameter (f) as a function of normalized distance of propagation (ζ) at different value of intensity parameter. The focusing is observed to be strongest in the case of intensity parameter 
${\rm \alpha} A_{00}^2 = 0.00025$. Further, self-focusing decreases with increase in intensity parameter beyond the 
${\rm \alpha} A_{00}^2 = 0.00025$. The self-trapping is observed to occur at 
${\rm \alpha} A_{00}^2 = 0.0027$. Thus, the beam propagates without convergence and divergence up to many Rayleigh lengths in the self-trapped mode, which is a key feature to the success of ICF and depends critically on long distance propagation of laser pulses at relativistic intensities (>1018 W/cm2).
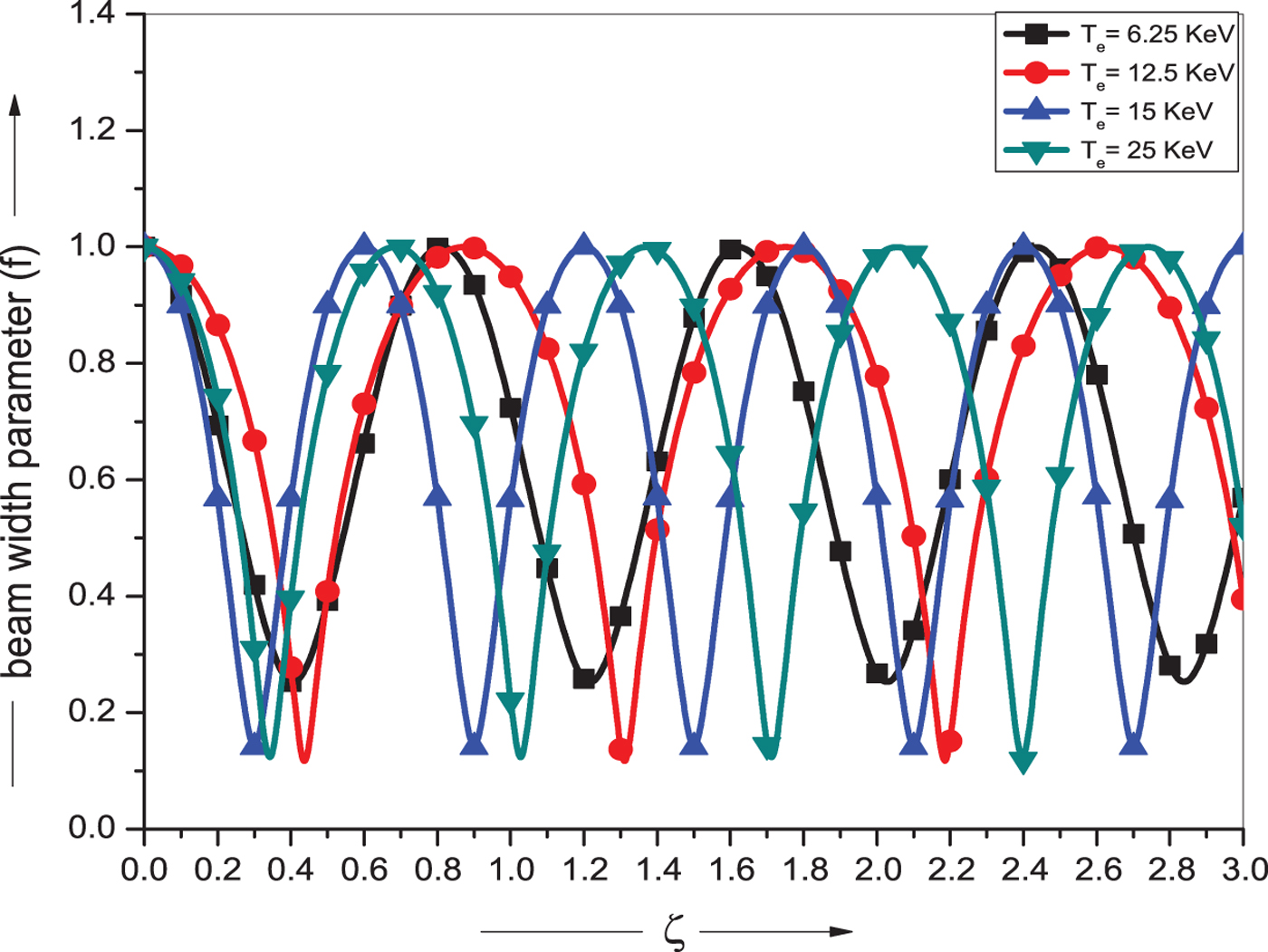
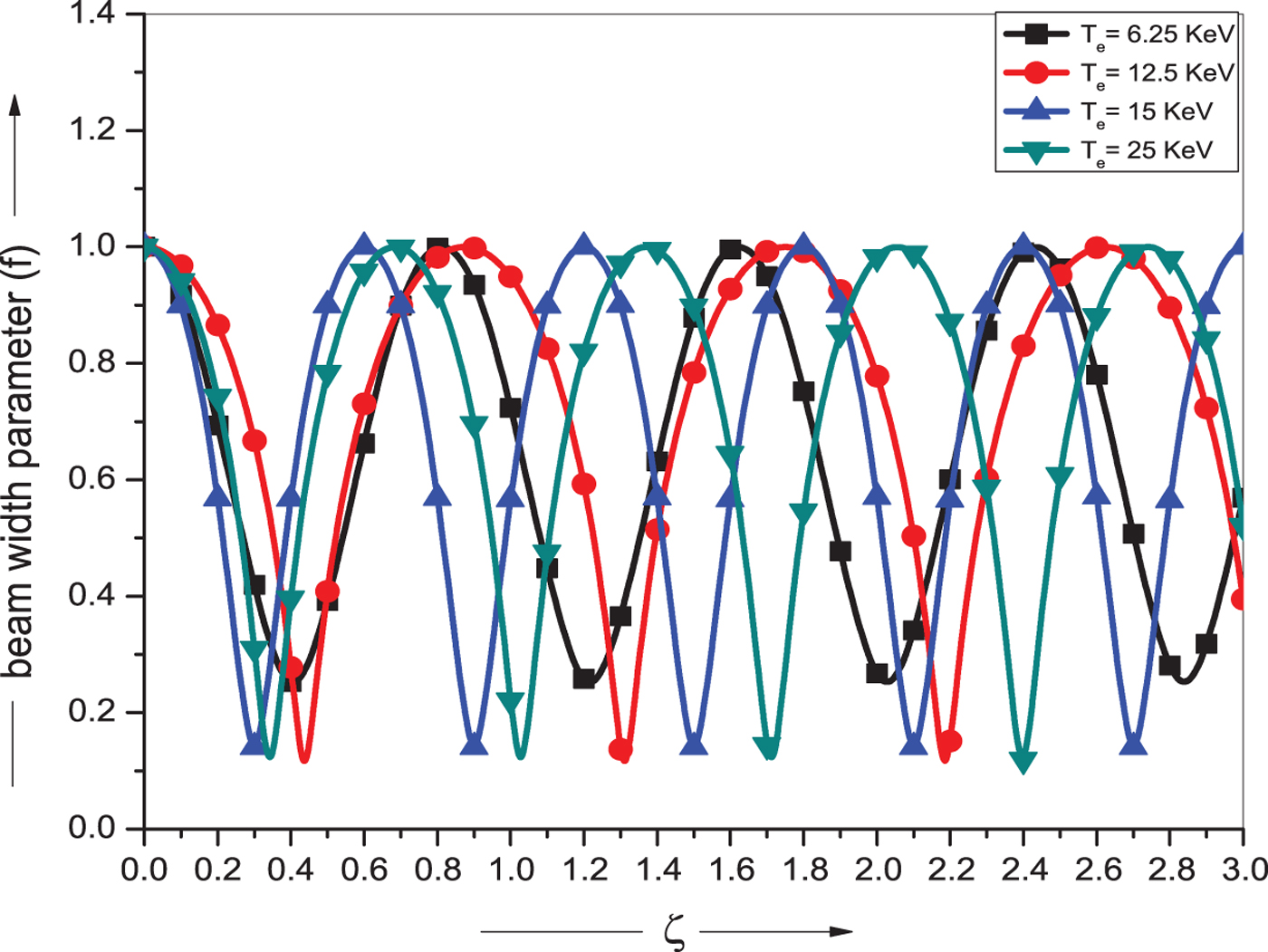
Fig. 5. Variation of beam width parameter f with normalized propagation distance ζ for relativistic ponderomotive cold quantum plasma (RPCQ) and for different value of electron temperature T e = 6.25, 12.5, 15 and 25 KeV. The other parameters are same as in Figure 1.
We have further plotted the variation of beam width parameter (f) as a function of normalized distance of propagation (ζ) for different values of electron temperature T e = 6.5, 12.5, 15, and 25 KeV as shown in Figure 5. The self-focusing is found to be strongest in case of T e = 15 KeV as elucidated from Figure 5, for which the plasma permittivity is maximum as observed in Figure 2. As we increase the electron temperature beyond 15 KeV, the self-focusing starts weakening with increasing focusing length. This is due to the fact that the non-linear term is sensitive to the electron temperature T e and relativistic factor γ, which further control the profile dynamics of the laser beam. A similar behavior is observed by Aggarwal et al. (Reference Aggarwal, Kumar and Kant2016), Wang and Zhou (Reference Wang and Zhou2011), and Milani et al. (Reference Milani, Niknam and Bokaei2014).
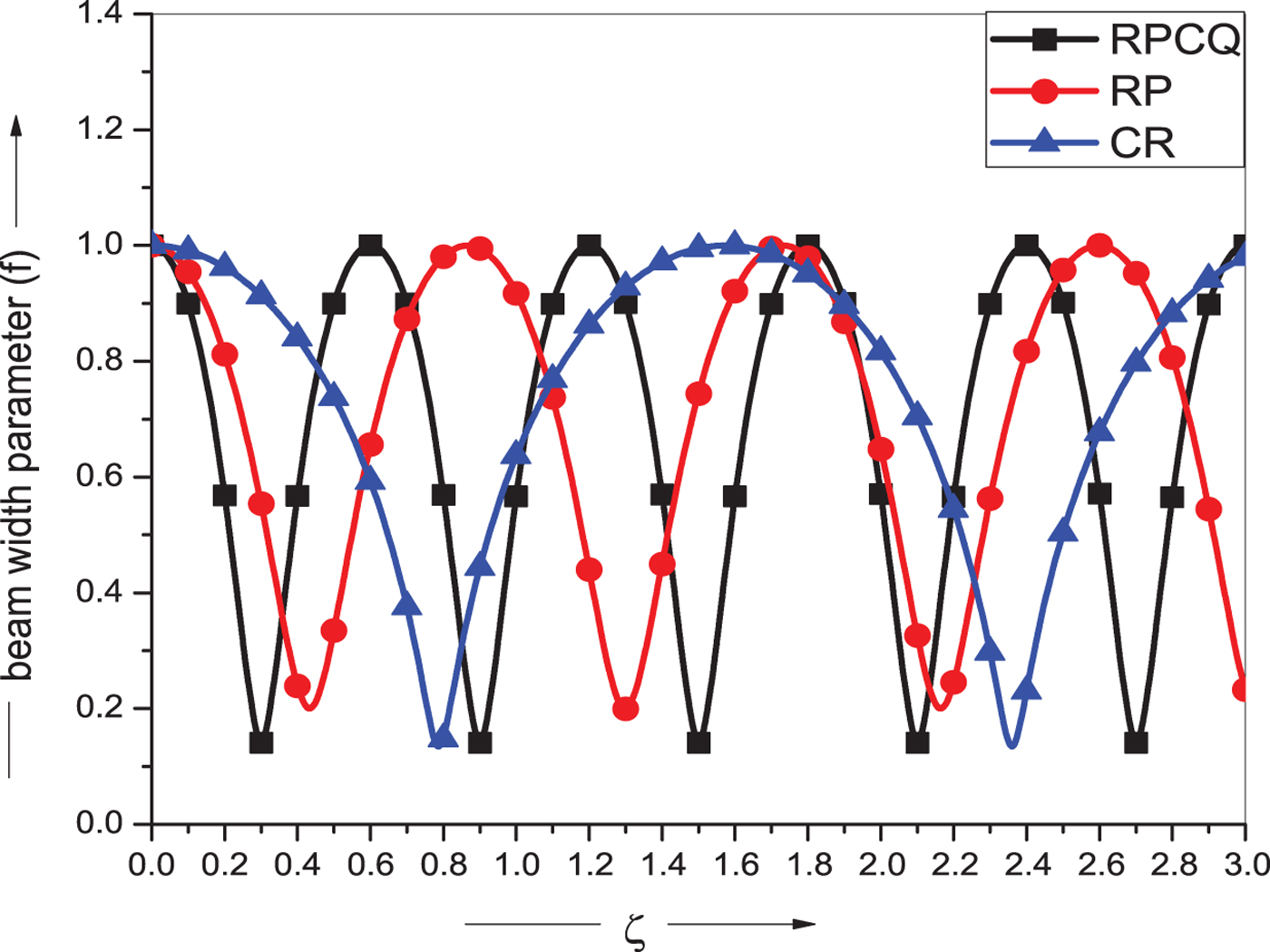
Figure 6 presents the variation of beam width parameter (f) as a function of normalized distance of propagation (ζ) for different types of plasma model, i.e., RPCQ, RP, and CR plasma. It is evident from the figure that strongest self-focusing is achieved for the RPCQ plasma model in comparison with those of RP plasma and classical relativistic (CR) case of reference. It is further concluded that quantum plasma acts as a non-linear medium and offered strongest self-focusing, thus acting as a catalyst in RP plasma. As a result, the laser beam is focused faster in quantum plasma and such a contribution of additional self-focusing is missing in RP and CR cases. Thus, self-focusing ability of laser beam in quantum plasma is better than both RP and CR case. These results are in agreement with the observation made by Aggarwal et al. (Reference Aggarwal, Kumar and Gill2017). The present investigation is helpful to the researchers to choose various laser and plasma parameters for enhancement in beam-focusing ability.
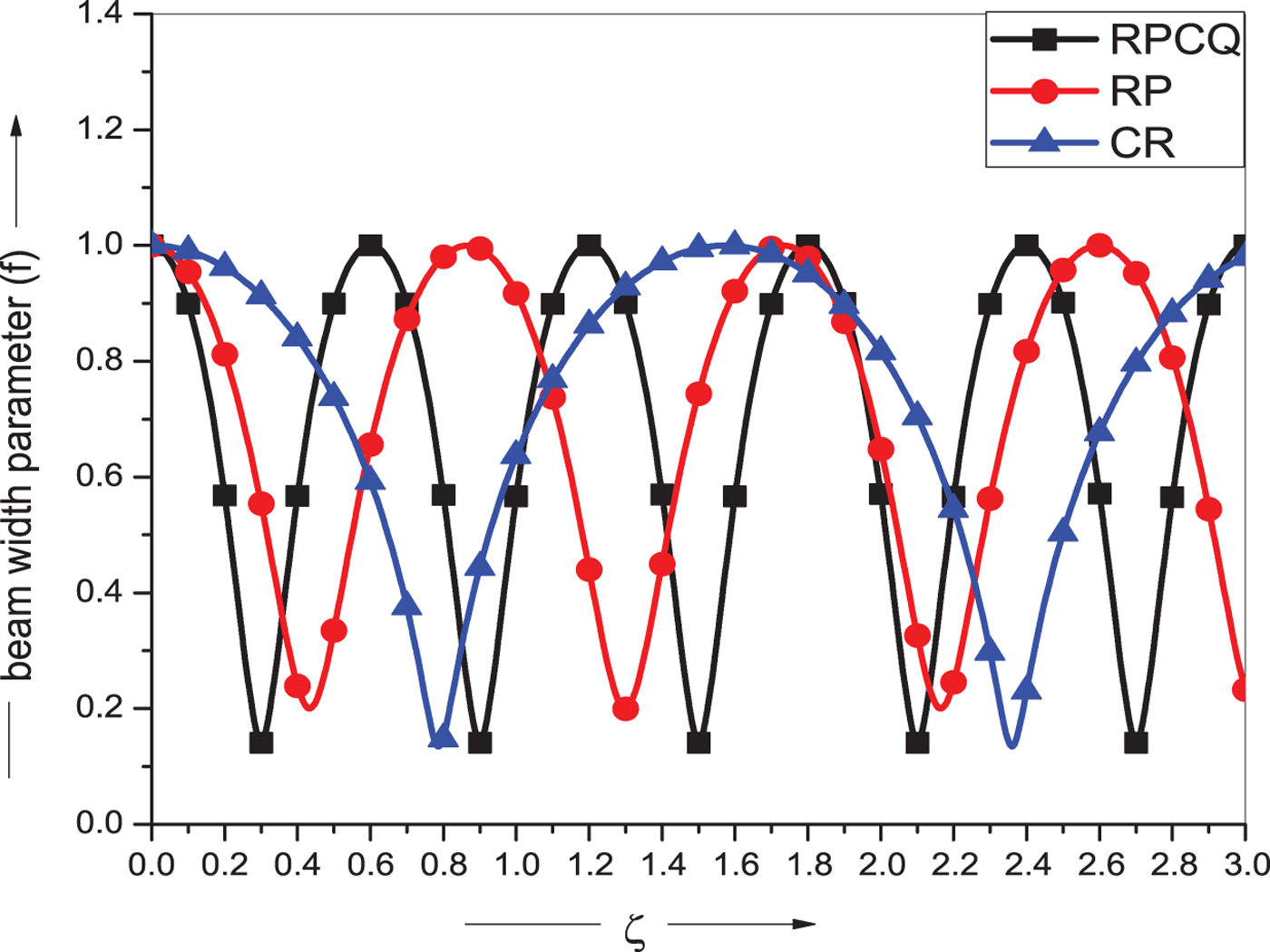
Fig. 6. Variation of beam width parameter f with normalized propagation distance ζ for relativistic ponderomotive cold quantum plasma (RPCQ), relativistic ponderomotive plasma (RP), and for classical relativistic (CR) case. The other parameters are same as in Figure 1.
Conclusion
In the present investigation, authors have investigated the self-focusing of quadruple Gaussian laser beam in weakly relativistic cold quantum plasma. Following conclusions are drawn:
1. Self-trapping of the quadruple beam is observed up to several Rayleigh lengths for the optimized set of laser and plasma parameters.
2. As quantum plasma acts as a non-linear medium, the strongest self-focusing is observed in case of RPCQ plasma in comparison with RP plasma and CR case of reference.
3. The beam width parameter of the laser beam is controlled by the initial intensity of the laser beam and electron temperature.
Our investigation may be useful in understanding the physics of high-power laser-driven fusion and in the fast ignition of modern ICF experiments, where the mechanism of laser propagation in the quantum plasma is important and quantum effects are dominant.
Acknowledgment
The authors Richa and Harish Kumar are thankful to the RIC of I.K. Gujral Punjab Technical University, Kapurthala (India) for their support.
