2. THEORY OF HOLE-BORING ACCELERATION

In a quasistationary piston model for the hole-boring RPA, the laser ponderomotive force pushes all electrons forward and then brings about a charge separation layer, while the ions left behind are pulled by the longitudinal electric field arising in this charge separation layer (Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009). Both the resulting hole-boring velocity ν_b and the accelerated ion energy ε_i can be derived from the momentum flux balance in the boosted frame moving with the laser-plasma interface as (Macchi et al., Reference Macchi, Cattani, Liseykina and Cornolti2005; Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009a; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009).

(1)$${\rm \nu}_b = c\Pi /\lpar 1 + \Pi \rpar \comma \; \, \, \, {\rm \varepsilon} _i = m_i c^2 2\Pi ^2 /\lpar 1 + 2\Pi \rpar \comma \;$$

with the speed of light in vacuum c, the ion mass m _i, and the hole-boring characteristic parameter Π defined as

(2)$$\Pi = \lpar I/{\rm \rho} c^3 \rpar ^{1/2} = a\lpar Zm_e n_c /2m_i n_e \rpar ^{1/2}\comma \;$$

where the dimensionless laser amplitude a = (Iλ²/1.37 × 10¹⁸ W cm⁻² μm²)^1/2, the critical density n _c = m _eε₀ω²/e ², ρ is the mass density, Z is the ionic charge state, m _e and n _e are the electron mass and density, and I, λ, and ω are the laser intensity, wavelength and frequency, respectively.

However, the previous studies indicated that the longitudinal electric field for accelerating ions always oscillates due to the periodic ejection of ion bunches from the charge separation layer (Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009a; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009). On the one hand, the steady hole-boring acceleration with a well-controlled oscillating field in one-ion-species targets only takes place under the condition a < n _e / n _c, i.e., with a sufficiently high plasma density or a relatively low laser intensity (Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009). Otherwise, the oscillation of the electric field may be obviously enhanced and the energy distribution of fast ions will be broadened, which seriously limits its applications. On the other hand, Eq. (1) indicates that the sufficiently high laser intensity and low plasma density are required for generating ions at high enough energy. In the following PIC simulations, however, we will show that the oscillation of the longitudinal electric field in the hole-boring RPA can be well suppressed even under the condition a ≥ n _e / n _c by using two-ion-species targets. Consequently, the energy spread of ion beams can be significantly reduced for accelerating the realization of its potential applications.

3. HOLE-BORING ACCELERATION IN TWO-ION-SPECIES TARGETS

The employed PIC code is similar to that used in previous investigations (Weng et al., Reference Weng, Mulser and Sheng2012a; Reference Weng, Murakami, Mulser and Sheng2012b; Reference Weng, Murakami, Azechi, Wang, Tasoko, Che, Sheng, Mulser, Yu and Shen2014). In all simulations, the pulse is assumed to be circularly polarized with the wavelength λ = 1.06 μm and thus the critical density n _c = 9.92 × 10²⁰ cm⁻³. The laser amplitude rapidly rises as asin (πt / 10τ) in the first five cycles and then keeps constant with a = 50 and τ = 2π / ω. The simulation box is located at −10λ ≤ x ≤ 70λ and simulations start from t = −10τ, where the laser pulse is launched from the left boundary x = −10λ. The targets with different components are all located at 0 ≤ x ≤ 50λ, and each one is initially cold with a homogeneous density. The spatial and temporal resolutions Δx = λ / 300 and Δ t = Δ x / c are used, and 20n _s / n _c macroparticles per cell are initially allocated for the particle species with density n _s.

Figure 1 shows the energy spectra of ions accelerated from three representative targets: (1) deuterium target, (2) tritium target, and (3) DT target with deuterons and tritons in 1:1 mass ratio. The electron number density varies in order to yield the same mass density ρ = 0.1 g cm⁻³ in all targets. Since the overall hole-boring dynamics are determined by the laser intensity and the target total mass density (Robinson et al., Reference Robinson, Kwon and Lancaster2009b), it is reasonable that ions are roughly accelerated to the same velocity and hence the ion spectra from three targets are all peaked at the same energy per nucleon (17.55 MeV/u) as predicted by Eq. (1). For the applied laser pulse a = 50, it is clear that the condition a < n _e / n _c fails for all targets. Therefore, it is expected that the resulting energy spectra should be quite broad. Indeed, this is true in the target with either pure deuterons or pure tritons. As shown in Figures 1a and 1b, the accelerated deuterons or tritons are broadly distributed over the energy spectrum with the respective energy spreads Δ E/E = 13.2% or 38.9%, here ΔE is the full width at the half maximum and E is the peak energy of the spectrum. However, the energy spectrum from the DT target surprisingly displays a favorable quality of being quasi-monoenergetic with a narrow spread 3.7% in Figure 1c. It is important to note that the principle of reducing the energy spread in the hole-boring RPA by using two-ion-species targets is essentially different from these in the TNSA or light-sail RPA. In the TNSA or light-sail RPA, the lighter ions such as protons are quickly separated from the heavier ions, then the heave ion layer acts as a substrate to protect the lighter ions from the instabilities and thus provide a more stable accelerating field for generating quasi-monoenergetic lighter ions (Yu et al., Reference Yu, Pukhov, Shvets and Chen2010; Cui et al., Reference Cui, Wang, Sheng, Li and Zhang2013). Usually, the energy spread of the lighter ions monotonously decreases with its ratio and the quality of heavier ion beams is sacrificed in the TNSA or light-sail RPA using two-ion-species targets. In the hole-boring RPA with two-ion-species targets, however, it is clear that the respective spectra of lighter ions (deuterons) and heavier ions (tritons) are very similar as shown in Figure 1c. They are almost peaked at the same energy per nucleon with narrow spreads 3.2% and 3.7%, respectively.

Fig. 1. Ion energy spectra at t = 100τ from PIC simulations. The laser amplitude is a = 50 and targets are: (a) deuterium target with n _e = n _D = 30n _c, (b) tritium target with n _e = n _T = 20n _c, and (c) DT target with n _D = 15n _c, n _T = 10n _c, and n _e = 25n _c. The respective spectra for deuterons (red dashed) and tritons (blue dash-dotted) from the DT target are also drawn in (c).

In order to understand the distinct ion energy spectra from different targets, it is essentially helpful to study the dynamics of accelerated ions. The time evolution of the density of only fast ions with energy ≥10 MeV are compared in Figure 2. As previously predicted, the accelerated ions by the hole-boring RPA will leave the charge separation layer in bunches rather than as a constant current because the laser pulse does not act as an ideal piston (Robinson et al., Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei2009a; Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009). This prediction is well illustrated by the streaks for fast deuterons or tritons in Figures 2a or 1b, respectively. It is clearly shown that the accelerated ions from one-ion-species targets are separated into bunches. The time interval among these ion bunches keeps nearly constant in the acceleration, and its value is inversely proportional to the ion plasma frequency (Schlegel et al., Reference Schlegel, Naumova, Tikhonchuk, Labaune, Sokolov and Mourou2009).

(3)$$\Delta t \propto \displaystyle{1 \over {{\rm \omega} _{\,pi} }} = \sqrt {\displaystyle{{m_i n_c } \over {m_e n_e }}} \displaystyle{1 \over {\rm \omega} }\comma \;$$

Fig. 2. Time evolution of the density of only fast ions with energy ≥10 MeV/u in different targets, the laser and target parameters are the same as in Figure 1.

While the accelerated deuterons and tritons from the DT target will depart from the charge separation layer in respective bunches because of their different plasma frequencies. Further, the time interval among ion bunches does no longer keep constant in the acceleration as indicated by the irregular bands of color in Figure 2c. As a result, the accelerated deuterons and tritons from the DT target are distributed into more bunches and each bunch bears less charge than these from the deuterium or tritium target.

Since the accelerated ions leave the charge separation layer in bunches, the total charge number in this layer will fluctuate. Consequently, the longitudinal electric field E _x oscillates as shown in Figure 3, in which the saffron yellow bands also roughly indicate the range of the charge separation layer. For the deuterium target, the saffron yellow band in Figure 3a contracts at the moments 95, 98, 101, 104τ, while the ejections of fast ion bunches also happen at the corresponding moments as shown in Figure 2a. The synchronization between the ejection of fast ion bunches and the contraction of charge separation layer is similarly identified by Figures 2b and 3b for the tritium target. For the DT target, we have found that the time evolution of the longitudinal electric field becomes smoother within a uniform charge separation layer as shown in Figure 3c. The time evolution of the magnitude of the longitudinal electric field are compared among three targets in Figure 4. It is shown that the relative oscillation of the field magnitude Δ E _{x, max} / E _{x, max} are roughly 40%, 42%, and 13% for the deuterium, tritium, and DT targets, respectively. This clearly indicates that the oscillation of the accelerating field in the hole-boring RPA can be effectively suppressed by using a DT target.

Fig. 3. Time evolution of the longitudinal electric field E _x in different targets, the laser and target parameters are the same as in Figure 1.

Fig. 4. Time evolution of the magnitude of the longitudinal electric field E _{x, max} in three different targets, the laser and target parameters are the same as in Figure 1.

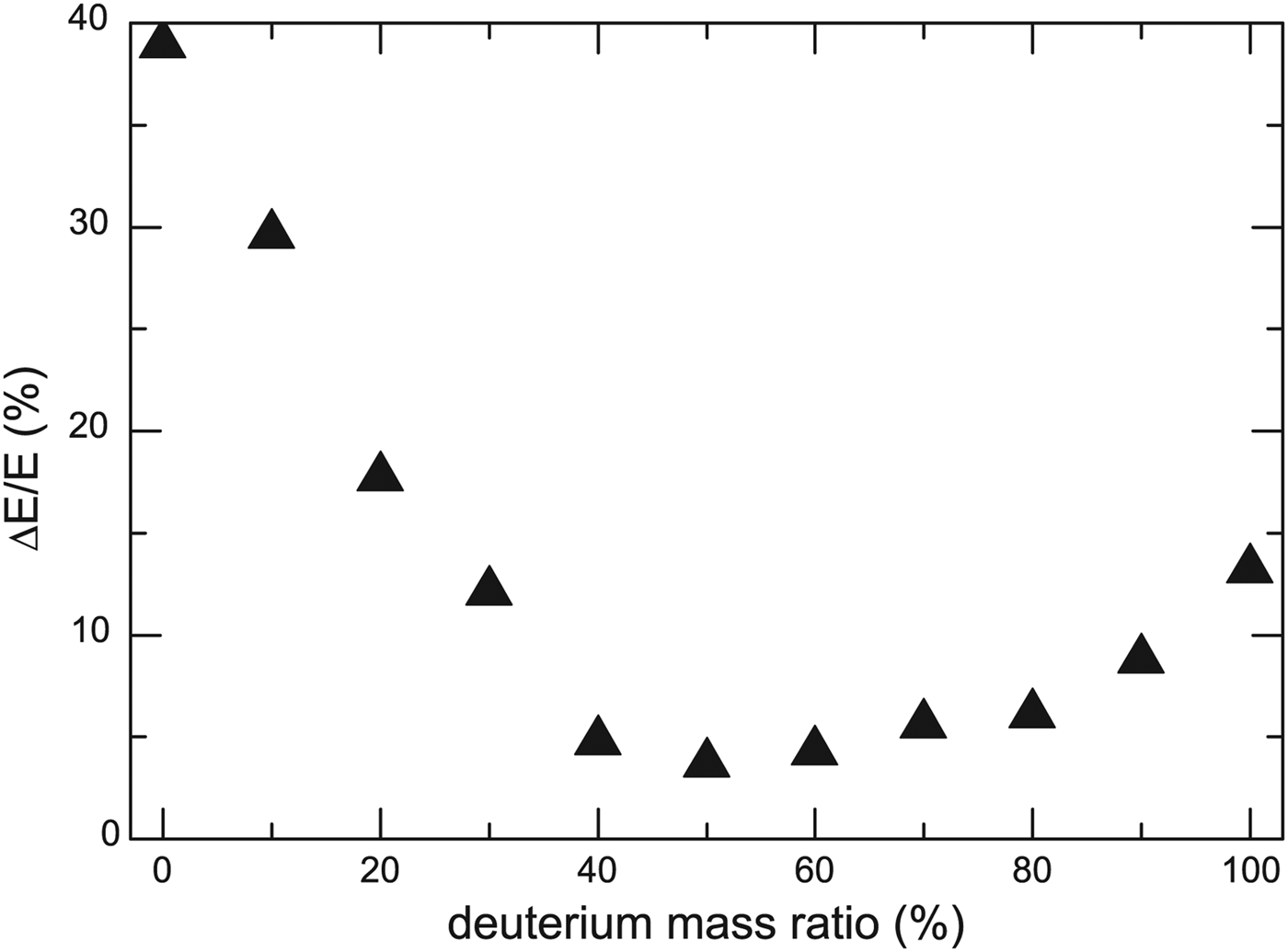
Fig. 5. Ion energy spread Δ E/E as a function of the deuterium mass ratio in the composite DT targets at t = 100τ from PIC simulations. The laser parameters are the same as in Figure 1, and the total mass density of composite targets is fixed at ρ = 0.1 g cm⁻³.

Finally, the effect of the mass ratio between deuterons and tritons in the composite targets are studied with the fixed total mass density ρ = 0.1 g cm⁻³. With the increasing mass ratio of deuterons, the energy spread of ion spectrum decreases dramatically at first, then it rebounds slowly as shown in Figure 5. The narrower energy spread from the pure deuterium target than the pure tritium target could be attributed to its higher electron density. Overall, it is clear that the narrowest energy spread is achieved roughly at the deuterium mass ratio of 50%.