Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T08:37:51.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Rayleigh–Taylor instability at a tilted interface in laboratory experiments and numerical simulations

Published online by Cambridge University Press:  03 March 2004

JOANNE M. HOLFORD ,
STUART B. DALZIEL  and
DAVID YOUNGS
JOANNE M. HOLFORD
Affiliation:
DAMTP, University of Cambridge, Cambridge, United Kingdom
STUART B. DALZIEL
Affiliation:
DAMTP, University of Cambridge, Cambridge, United Kingdom
DAVID YOUNGS
Affiliation:
AWE Reading, Berkshire, United Kingdom
Rights & Permissions [Opens in a new window]

Abstract

This article investigates the molecular mixing caused by Rayleigh–Taylor (RT) instability of a gravitationally unstable density interface tilted at a small angle to the horizontal. The mixing is measured by the increase in background potential energy, and the mixing efficiency, or fraction of energy irreversibly lost to fluid motion doing work against gravity, is calculated. Laboratory experiments are carried out using saline and fresh water, and modeled with compressible numerical simulations, with a suitable choice of parameters and initial conditions. The experiments show that the high cumulative efficiency of mixing in RT instability at a horizontal interface is only slightly reduced by an interface tilt of up to 10°, despite the strong overturning that occurs. Instantaneous mixing efficiencies as high as 0.5–0.6 are measured, when RT instability is active, with lower values of about 0.35 during the subsequent overturning. The numerical simulations capture the most unstable scales and the overturning motion well, but generate more mixing than the experiments, with the instantaneous mixing efficiency remaining at 0.5 for most of the run. The difference may be due to restratification at small scales in the high Prandtl number experiments.

Keywords

Mixing efficiencyMolecular mixingRayleigh–Taylor instability
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 419 - 423
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

Rayleigh–Taylor (RT) instability occurs at the interface of a fluid of density ρ1 accelerated by a pressure gradient, such as that produced by gravity g, into a fluid of density ρ2 < ρ1. The instability is related to the Richtmyer–Meshkov instability of an impulsively accelerated interface, such as that between layers of an imploded inertial confinement fusion capsule. Neglecting viscous or diffusive effects, the governing parameter is the Atwood number A = (ρ1 − ρ2)/(ρ1 + ρ2) = Δρ/2ρ0, where ρ0 = (ρ1 + ρ2)/2 is the mean density and Δρ = (ρ1 − ρ2) is the density difference. The linear growth rate of disturbances of wavelength λ is

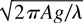
, so that all scales are unstable, and shorter scales grow faster. As a result, the interface becomes highly convoluted and the fluids mix. The degree of molecular mixing is a control on the evolution of reactive fluids. Previous work has shown the sensitivity of mixing to the initial conditions (Linden, Redondo & Youngs, 1994; Cook & Dimotakis, 2001).

The simplest situation is the instability of an almost planar interface perpendicular to the driving acceleration, for example, a horizontal interface under the acceleration of gravity. In practical situations, RT instability has more complex initial conditions. One simple configuration is that of a gravitationally unstable planar interface tilted away from the horizontal. At this interface, there is competition between the local instability and a large-scale overturning, which does not contribute significantly to mixing of the fluids. We study this situation using incompressible laboratory experiments, in salt and fresh water, and compressible numerical simulations.

2. MIXING

While stirring or reversible mixing causes the interleaving of fluid with different properties, diffusion causes irreversible mixing by the homogenization of fluid properties at the molecular scale. It is only when fluids are irreversibly mixed that chemical reactions occur. Within a fluid of varying density in a gravitational field, molecular mixing changes the potential energy (PE) of the fluid, and these changes can be quantified as a mixing efficiency η. For a stably stratified fluid initially at rest, stirred by an energy input and returning to rest, η is defined as the increase in PE as a fraction of the energy added. In the mixing of stably stratified fluids, measurements show η < 0.2, and are often an order of magnitude less. In contrast, measurements of η in RT mixing by Linden and Redondo (1991) show relatively high values of η ≈ 0.3–0.4.

In an incompressible fluid, the total mechanical energy E comprises kinetic energy (KE) and PE, E = ∫V½ρ|u|2 + ρgz dV, and in a closed system this total decays in time,

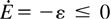
, due to energy dissipation ε. Following Lorenz (1955) and Winters et al. (1995), E can be decomposed into two components, the background energy Eback, defined as the minimum energy the fluid can take up if parcels are rearranged with no molecular mixing, and available energy Eavail = E − Eback. The only contribution to Eback is from the PE, and is found by rearranging the parcels in order of decreasing density with height. As irreversible mixing can only bring the mass of any two fluid parcels closer together and raise the center of mass of the reordered fluid,

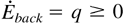
. Then we can extend the definition of mixing efficiency to systems with nonzero available energy, as in Caulfield and Peltier (2000), to give the cumulative mixing efficiency ηcumulative in the time interval (t0, t),

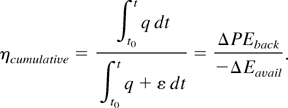
Additionally, we can calculate an instantaneous mixing efficiency ηinstantaneous,

Both quantities lie in the range 0 ≤ η ≤ 1.

For a compressible fluid, the internal energy (IE) e per unit mass contributes to the total energy, E = ∫V½ρ|u|2 + ρgz + ρe dV. The minimum energy the system can attain by adiabatic rearrangements (without molecular mixing) is Eback = IEback + PEback, sketched in Figure 1. The total energy is now conserved,

. Dissipation increases the background IE,

, while molecular mixing increases the background PE,

. Definitions (1) and (2) still apply, so that the mixing efficiency is always the fraction of energy lost to fluid motion (reduction in Eavail) doing work against gravity (gain in Eback).

Partition of energy in a compressible fluid.

2.1. Laboratory experiments

The experiments were carried out in the tank used by Dalziel, Linden and Youngs (1999), in which a barrier separating saline and fresh water was removed to initiate the instability. A hollow barrier threaded with fabric was used to reduce the shear at the unstable interface, and Dalziel et al. (1999) quantified the remaining disturbance as a large-scale overturning. In the present experiments, the whole tank was tilted at an angle to the horizontal.

Image analysis techniques were used to measure either the density or velocity field in an illuminated vertical plane along the center of the tank. For density measurement, the dense fluid was dyed with fluorescent dye, and the density calculated from images corrected for light sheet divergence and attenuation. For velocity measurement, the fluid was seeded with neutrally buoyant particles, and Lagrangian particle tracks identified. The sensitivity to the initial conditions precluded deriving a useful ensemble mean flow. Instead, the particle tracks were gridded at two scales, onto 1-cm and 3-cm grids, giving the resolved velocity and the mean overturning flow, respectively. Assuming isotropy at scales smaller than the mean flow gave an estimate of the KE in that plane. Assuming statistical homogeneity across the tank, the in-plane measurements were scaled to estimate the mechanical energy in the flow.

Atwood numbers in the range 0.5 × 10−3 < A < 2.5 × 10−3 were used, implying that the flow was Boussinesq. The tank height H sets a timescale

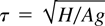
, in the range 10 s > τ > 4.5 s. The RMS velocities were 0.8 cms−1 < |u| < 2 cms−1, and integral length scales 1.8 cm < l < 2.5 cm, giving a turbulent Reynolds number in the range 150 < Re < 500. The experiments do not show a Reynolds number dependence across this range.

2.2. Numerical simulations

Simulations using Turmoil 3D, a compressible finite volume code, were run to model the mixing of two ideal gases in the experimental geometry. The resolution of 200 × 160 × 80 was the same as in Dalziel et al. (1999). A loss of resolution at the grid scale provides numerical diffusion, mimicking molecular mixing (as it smoothes mass fraction), and dissipation (as it smoothes velocity). At each step, the reduction in KE was calculated and added to the IE, to ensure conservation of total energy. In some runs, an explicit viscosity was also added. The normalisation H = 1, Ag = 1, and ρ1 = 1 was chosen, leaving the gravitational acceleration g and the pressure at the center of the undisturbed interface p0 as parameters. There are then two nondimensional parameters, other than geometric factors: the density ratio B = Δρ/ρ0 = 2/g and the Mach number

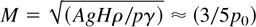
. To model an incompressible Boussinesq fluid, we require both B, and the ratio I = gHρ2/5pΔρ ≈ g2/10p0 which compares the density change across the domain due to compressibility with the density change at the interface, to be small. Therefore we chose g = 11 and p0 = 100, giving B ≈ 0.18, M ≈ 0.08, and I ≈ 0.12.

In a homogeneous fluid at rest, vertical momentum conservation requires that the fluid be in hydrostatic balance. Then for neutral stability, the buoyancy frequency N, given by

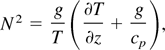
for a fluid of temperature T and specific heat at constant pressure cp, must be zero. For neutral stability within each of the ideal gas regions, this implies that the fluid is isentropic, with p = k(s)ργ, where k is a function of the entropy s and γ is the heat capacity ratio. The two fluids are therefore chosen to have uniform but differing entropy. The specific heats of the two fluids are chosen so that the temperature is continuous at the interface. When the interface is not horizontal, the initial pressure cannot be hydrostatic. In fact, for an incompressible response from the fluid, we require that the initial time rate of change of the velocity divergence ∇.u is zero. Ignoring terms of O(u2), this implies that

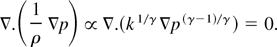
This is solved subject to the boundary condition that

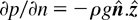
, where

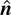
is the outward normal. Alongside this initial pressure field, a weak two-dimensional initial velocity field is added to represent the perturbation induced by removal of the barrier, based on the measured perturbation for the untilted tank (Dalziel et al., 1999). A three-dimensional random perturbation, with wavelengths L/40 < λ < L/20 and rms amplitude σ = H/2500 where L is the width of the tank, is added to the interface position.

3. RESULTS

Figure 2 shows the volume fraction and out-of-plane vorticity field in the measurement plane at two times, from laboratory experiments and a comparable simulation. The rate of overturning and dominant wavelength of growth is well matched, within the experimental variability. The energy budgets for these two sequences are shown in Figure 3. The PE scale is chosen so that a well-mixed fluid has PE = 0, and the energy normalization so that initially PE = 1. Although the initial PE decrease compares well, the simulation develops more KE than the experiment. Further differences occur in the decaying phase of the flow, when the KE in the simulation remains higher than in the experiment, and mixes the two components for longer. The increase in PEback corresponding to molecular mixing is limited to t/τ < 5 in the experiments, but continues for t/τ < 8.5 in the simulations. In terms of mixing efficiency, the experiments give ηinstantaneous ≈ 0.35 apart from t/τ ≈ 1 and 7, when RT instability occurs and ηinstantaneous is greater, and over the course of the experiment, ηcumulative = 0.38. In the simulation, ηinstantaneous ≈ 0.5 is maintained for most of the run, so that in total the mixing is more efficient, with ηcumulative = 0.49. The difference in energy budgets does not appear to be due to the character of numerical diffusion, as the total dissipation was unaffected by the ratio of explicit/numerical viscosity until the explicit viscosity was dominant. The difference may be due to the restratification of stirred fluid elements in the experiments (at Prandtl number Pr = ν/κ = 700), below the scale resolved by the simulations, which have a numerical Prandtl number of unity. In experiments, as the initial interface angle increases from 0° to 10°, ηcumulative falls from 0.4 to 0.33, showing that the overturning decreases the mixing only slightly.

Fields from the central vertical plane in experiments (left) and a simulation (right). Volume fraction at t/τ = 1.8 (a), t/τ = 6.0 (b), and vorticity at t/τ = 1.8 (c), t/τ = 6.0 (d), with velocity arrows on the experimental data.

Time evolution of KE (dotted), PE (dashed), PEback (dot-dashed) and ηinstantaneous (solid) in experiments (a) and simulations (b).

4. CONCLUSIONS

The high efficiency of mixing by RT instability is confirmed, with measurements for cumulative mixing efficiencies of around 0.4 for a horizontal interface. As the tilt of the interface increases, the mixing efficiency falls only slightly. Instantaneous values as high as 0.5–0.6 are measured. By a suitable choice of nondimensional parameters, compressible three-dimensional numerical simulations can be used to model the experiments. In particular, a novel condition on the pressure and entropy is required to ensure that no pressure waves are excited by the initial conditions. Good agreement is found in the large-scale overturning features of the flow; however the numerical code mixes more efficiently than the laboratory experiments, possibly due to restratification at small scales in the experiments. Further work is in progress to resolve these issues, and to investigate the changing nature of the instability when the interface is at a larger angle to the horizontal.

References

REFERENCES

Caulfield, C.P. & Peltier, W.R. (2000). Mixing in stratified shear flows: Dependence on initial conditions. Proc. of 5th Int. Symp. on Strat. Flows, (Lawrence, G.A., Pieters, R. and Yonemitsu, N., Eds.), pp. 483–488.
Cook, A.W. & Dimotakis, P.E. (2001). Transitional stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.Google Scholar
Dalziel, S.B., Linden, P.F. & Youngs, D.L. (1999). Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
Linden, P.F. & Redondo, J.M. (1991). Molecular mixing in Rayleigh–Taylor instability. Part I. Global mixing. Phys. Fluids A 3, 1269–1277.Google Scholar
Linden, P.F., Redondo, J.M. & Youngs, D.L. (1994). Molecular mixing in Rayleigh–Taylor instability. J. Fluid Mech. 265, 97–124.CrossRefGoogle Scholar
Lorenz, E.N. (1955). Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167.Google Scholar
Winters, K.B., Lombard, P.N., Riley, J.J. & D'Asaro E.A. (1995). Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar
Figure 0

Partition of energy in a compressible fluid.

Figure 1

Fields from the central vertical plane in experiments (left) and a simulation (right). Volume fraction at t/τ = 1.8 (a), t/τ = 6.0 (b), and vorticity at t/τ = 1.8 (c), t/τ = 6.0 (d), with velocity arrows on the experimental data.

Figure 2

Time evolution of KE (dotted), PE (dashed), PEback (dot-dashed) and ηinstantaneous (solid) in experiments (a) and simulations (b).