Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T08:02:30.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Radiation loss from inertially confined degenerate plasmas

Published online by Cambridge University Press:  25 March 2004

SHALOM ELIEZER ,
PABLO T. LEÓN ,
JOSÉ M. MARTINEZ-VAL  and
DIMITRI V. FISHER
SHALOM ELIEZER
Affiliation:
Soreq Nuclear Research Center, Yavne, Israel
PABLO T. LEÓN
Affiliation:
Institute of Nuclear Fusion, Escuela Técnica Superior de Ingenieros Industriales, Universidad Politécnica de Madrid, Spain
JOSÉ M. MARTINEZ-VAL
Affiliation:
Institute of Nuclear Fusion, Escuela Técnica Superior de Ingenieros Industriales, Universidad Politécnica de Madrid, Spain
DIMITRI V. FISHER
Affiliation:
Soreq Nuclear Research Center, Yavne, Israel
Rights & Permissions [Opens in a new window]

Abstract

Bremsstrahlung is one of the most important energy loss mechanisms in achieving ignition, which is only possible above a threshold in temperature for a given fusion reaction and plasma conditions. A detailed analysis of the bremsstrahlung process in degenerate plasma points out that radiation energy loss is much smaller than the value given by the classical formulation. This fact seems not useful to relax ignition requirements in self-ignited targets, because it is only relevant at extremely high densities. On the contrary, it can be very positive in the fast ignition scheme, where the target is compressed to very high densities at a minimum temperature, before the igniting beamlet is sent in.

Keywords

BremsstrahlungDegenerate plasmaFusionIgnitionRadiation
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 599 - 607
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION AND SCOPE

The classical approach to produce ignition in fusion plasmas is to heat them up to a temperature high enough for the fusion-born charged particle energy to overcome radiation emission. This approach is followed both in magnetic confinement, where plasmas are underdense, and inertial confinement, where plasmas are compressed to very high densities.

Although standard schemes (Bodner 1981, Brueckner & Jorna, 1973; Kidder, 1979; Meyer-ter-Vehn, 1982; Martìnez-Val et al., 1994; Tahir & Hoffmann, 1994; Atzeni, 1995, 2002) of inertial fusion research do not take into account plasma degeneracy, inertial compression could produce them according the lines established in the shock-multiplexing implosion scheme (Kidder, 1974; Yamanaka et al., 1986, 1987; Yamanaka & Nakai, 1986), which got 600 times compression with moderate laser beam energy (Nakai et al., 1991) in a series of experiments carried out at the end of the 1980s, particularly with spherical polymer shells, where a compression factor of 1000 times was achieved (Azechi et al., 1991). However, the interest of inertial fusion research focused on different implosion schemes, yielding moderate densities (∼20 g/cm3) with high electron temperatures (∼1 keV), which correspond to a classical plasma (Yaakobi et al., 1999). Nevertheless, the same laboratory had obtained higher densities in compressed targets 10 years before (McCrory et al., 1988) depending on the tailoring of the implosion pulse and the target structure.

In the standard approaches formerly cited, targets were self-ignited either from a central hot spark or from a larger domain (volume ignition). A different scheme was proposed in the fast ignition model (Tabak et al., 1994), where the target is highly compressed at a temperature as low as possible, and ignition is triggered by sending a powerful ultrashort beam of the required energy. In this case, the interaction phase between the ignition beam and the target is of primary importance (Deutsch, 1997; Kato et al., 1997; Piriz & Sanchez, 1998; Boreham et al., 1999; Key, 2001; Kodama et al., 2001; Norreys et al., 2000; Roth et al., 2001) but is worth pointing out that the compressed target can be in a degenerate state when the igniting beam is launched. Although the igniting region will be heated to a very high temperature in a very short time, a significant fraction of the reacting plasma can still be at a degenerate state. It is therefore very important to analyze radiation emission from degenerate plasmas, in the framework of fast ignition.

Radiation losses in inertial targets are dominated by bremsstrahlung. Inverse Compton can additionally transfer energy from electrons to photons (Eliezer & Martinez-Val, 1998), but this mechanism is not significant if the electron temperature is moderate or low, as is the case in degenerate plasmas. A comprehensive review of atomic physics processes in very dense plasmas can be found elsewhere (More, 1993).

The possibility of using degenerate plasmas for inertial fusion was recently outlined in a macroscopic approach (Leon et al., 2001) but a more accurate and detailed analysis for the relevant physical mechanisms inside the plasma was needed. In the following, radiation loss by bremsstrahlung emission is studied from the starting point of electron-photon energy transfer through its integration in the Fermi–Dirac distribution. It must be taken into account that most of the low level energy states in the electron statistics are already occupied, and a very broad range of electron transitions are forbidden.

This subject was already studied by Totsuji (1985) with a general purpose, not specifically oriented to fusion applications. Besides that, in our analysis, a clear connection between the degenerate and the classical case is obtained. It is clearly seen that there is a transition temperature, for a given plasma density, below which the degenerate emission rate applies. On the other hand, bremsstrahlung emission follows the classical formula for higher temperatures.

After analyzing in detail bremsstrahlung emission in degenerate plasmas, the corresponding equation is applied to the definition of ignition temperature. In targets compressed to very high densities, as those sought in the fast ignition concept, it is found that the ignition temperature is lower than the classical one, because of bremsstrahlung emission reduction.

2. BREMSSTRAHLUNG FUNDAMENTALS

The spectral distribution of radiation emitted by a monoenergetic electron beam of unit intensity scattered by an ion of charge Ze, is (Miyamoto, 1980) in SI units

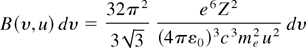
for hυ ≤ ½me2u2, being 0 for hυ ≥ ½me2u2. In the foregoing expressions, υ is the photon frequency, and u stands for the electron speed. No relativistic correction has been included because the electron temperature Te (in energy units) is much lower than me c2.

It must be noted that Bdυ has units of J·m2, and it can be integrated to give the radiation power density w(ν) dν emitted from a plasma with an ion density ni and an electron density ne. In the case of having multiple ion species, a summation over the ion species must be extended. We first recall that the classical integration is

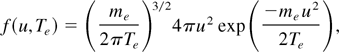
where umin = (2hν/me)1/2 is the minimum electron speed to generate an hν photon, Te is given in energy units and f (u,Te) is the classical Maxwellian distribution.

In the degenerate case, the energy electron distribution follows the Fermi–Dirac expression (see, e.g., Eliezer et al., 1986):

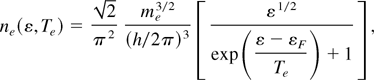
where the Fermi energy, εF (known also as the chemical potential) plays a fundamental role, and depends on electron density and Te.

For Te << εF0,

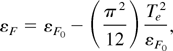
where

It is worth noting that the probability of state with energy ε to be occupied is

In particular, for Te = 0, all energy states ε < εF are fully occupied, whereas all states ε > εF are empty. When Te increases (still in the degenerate case, and therefore Te < εF) transition from ε < εF to ε > εF becomes not so sharp, and some electrons can be found with ε > εF. Because of the forbidden electron transitions in the degenerate case, Eq. (3) is no longer valid, and ne f (u,Te) must be substituted by a term properly taking into account that most of the low energy states are fully occupied, and an electron cannot fall into them after emitting a photon. Hence, ne f (u,Te) in Eq. (2) must be replaced by

where ne(ε,Te) is given by Eq. (4).

The total radiation loss expressed in terms of power density is

where the spectral power density is now

and

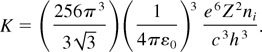
The integrand of Eq. (10) is depicted in Figure 1. The degeneracy effect is clearly seen.

Integrand of Eq. (10) for a degenerate plasma with εF0 = 3.65 keV and Te = 100 eV. It is observed that the integrand vanishes for all energies except those close to εF0, and for small values of hν. For other electron and photon energies, bremsstrahlung emission is not possible.

The spectrum is obtained by integrating Eq. (10). Defining the degeneracy parameter by

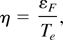
one gets for the spectrum

and F1/2(η) is the corresponding Fermi–Dirac integral function. The total bremsstrahlung power density in a degenerate plasma, characterized by ne and Te is obtained by integrating Eq. (13)

Fermi–Dirac integrals are given below, with the corresponding limits for η >> 1 (degenerate case)

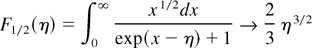
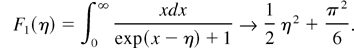
If bremsstrahlung emission in the degenerate case is compared to the value of the classical case, we find the exact result

For η >> 1, which corresponds to a fully degenerate case, the last equation can be rewritten as

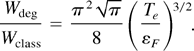
For instance, if Te = 0.1εF in the degenerate plasma, its bremsstrahlung loss will be about 7% of the radiation loss from a classical plasma at the same temperature. However, this comparison is not totally accurate. If the plasmas have the same temperature, the density of the degenerate case will be much larger than that of the classical case. If they have the same density, they will have different temperatures (much lower in the degenerate case). A more comprehensive analysis is presented in the following section.

3. RADIATION LOSSES REGIMES IN INERTIAL FUSION PLASMAS

In our analytical model, the fully degenerate case corresponds to η >> 1 [Eq. (12)]. Note that the electron density can be written as

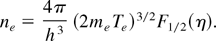
If ne and Te are given, the value of the Fermi–Dirac integral F1/2(η) is derived from them, using the last equation. The value of η is then calculated from Eq. (15). In very degenerate cases, the approximate value (3/2F1/2)2/3 can be used. Once η is known, the Fermi energy εF(Te) is directly derived from Eq. (12).

When using the degenerate model, the classical limit is theoretically achieved for η → −∞. This is so because of the difference between Fermian and Maxwellian energy distributions. It can be checked that the degenerate model goes exactly to the classical one as η → −∞. Equation (17) equals one in this limit.

In the classical case, bremsstrahlung emission goes as Te1/2. In the degenerate case, it goes as Te2. Figure 2 shows the bremsstrahlung power density for various density values, as a function of Te. Below a certain Te value, for a given density, bremsstrahlung emission follows the degenerate case expression. On the contrary, for upper temperatures, it corresponds to the classical case. A short Te range is observed as the transition regime from one to another. Of course, the transition temperature increases with density.

Bremsstrahlung emission power from a deuterium–tritium plasma as a function of Te, for various electron densities. Each line shows a low Te range, corresponding to degenerate cases, and a high Te range, for classical plasmas. The fitting between both regimes is very smooth.

Additional information is given in Figure 3, where the ration of the radiation emission in the degenerate case to the value of the classical case is depicted. It is seen that the ratio becomes 1 above the transition temperature, and decreases very fast as temperature decreases below it. Such a feature will be analyzed later on in order to find out whether it is possible to reduce the fusion ignition temperature by compressing the targets up to degenerate levels.

Ratio between the bremsstrahlung power of degenerate cases and the power of classical ones, for different temperatures. At temperatures lower than the transition value, the classical formulation is not valid.

Spectral differences are also observed between classical and degenerate cases, as can be seen in Figures 4 and 5. In Figure 4, spectral distribution of photons is given for a classical case and a degenerate case, both of them with an electron density of 1.81 × 1023 cm−3. Fermi energy is in this example εFO = 11.68 eV. In the degenerate case, the temperature is 3.5 eV (η = 3). In the classical one, it is 30 eV. The spectral shapes (in semilog scale) are the same at medium and high photon energies, but they are different at low values, where the degenerate case does not have a constant slope, which is a typical feature of the bremsstrahlung spectrum from classical plasmas. Therefore, it is worth pointing out that the degenerate case has a special signature, as can be seen in a more clear way in Figure 5. The density chosen in these calculations can represent a solid surface plasma of aluminum irradiated by femtosecond lasers of the appropriate power (less than 1014 W/cm2). The aluminum layer does not have time to expand, and Z = 3 is produced by the conduction band electrons. This spectral information can be useful to properly understand radiation emitted from that surface, and can also help analyze compression conditions of inertially confined targets.

Bremsstrahlung spectrum for different cases. Classical plasmas show a straight line in the semilog scale. In the degenerate case, the slope changes for small values of hν.

Ratio of bremsstrahlung spectrum of a degenerate plasma to the spectrum obtained from the formulation of the classical case. The ratio is 1 when the case has a negative η value (classical domain) because the degenerate case formulation tends to the classical one a η → −∞ (for practical purposes, as η ≤ −5).

4. IGNITION TEMPERATURE IN DEGENERATE PLASMA: THE CASE FOR FAST IGNITION

We will follow the standard definition of the ignition temperature as the value for which the fusion-born charged particle power equals the radiation loss power. A calculation has been carried out for the stoichiometric deuterium–tritium plasma, featured by the following fusion reactivity value (in m3/s):

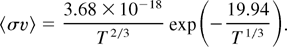
In this formula, T is given in kiloelectron volts. Ions are not degenerate and have a Maxwellian velocity distribution.

In Figure 6, bremsstrahlung power and fusion-born alpha-particle power are plotted versus temperature for different density values. For the lower density (1025 electrons per cm3), the crossing between both lines (bremsstrahlung power and fusion power) belongs to the classical region, clearly identified by the slope of bremsstrahlung emission (as T1/2). On the contrary, for the highest electron density in the figure, 1029 cm−3, the crossing point corresponds to the degenerate case, and it is slightly below 1 keV, that is, somewhat lower than the standard ignition temperature, 4.5 keV. It is also seen from the picture that the electron density has to be over 1027 cm−3 for the degeneracy effects to be relevant to decrease the ignition temperature. For this density, the transition temperature between both bremsstrahlung regimes lies slightly below the classical ignition temperature, that is 4.5 keV.

Bremsstrahlung power and alpha-particle power for stoichiometric deuterium-tritium, as a function of T, for different electron densities. When this one is above 1027 cm−3, the low ignition temperature regime appears.

It is worth pointing out that 1027 cm−3 is an extremely high electron density, more than 20,000 times DT solid density. In inertial fusion schemes based on self-ignited targets, such a compression factor seems to be out of reach, because it would need a very powerful and very symmetric spherical implosion with the formation of a central hot spark.

However, targets compressed for fast ignition could be degenerate because the main objective is to precompress the full target to very high densities at very low temperatures. During ignition, a complex interaction phase will develop, and a fraction of the ignited region will become hot and classical, but a significant fraction of the igniting region will actually start burning when it still is a degenerate plasma, because of the significant reduction in the radiation loss. Therefore, ignition requirements in the fast ignition concept could be significantly relaxed by the aforementioned reduction in the bremsstrahlung emission power. To produce degenerate plasmas in the compressed targets, fuel preheating must be avoided during the compression phase. Otherwise, such very high density values as those formerly cited in our calculations could not be attained.

Note that in the former analysis, ion and electron temperatures have been assumed to be equal. However, if a charged particle beam is used as an igniting trigger (Roth et al., 2001) the ion temperature in that region will be larger than the electron temperature, and this factor will also contribute to keep electron degeneracy for a longer while, thus reducing radiation losses. In fact, the interaction of charged particles with a degenerate plasma (Skupsky, 1977; Maynard & Deutsch, 1982) will become very important in this context and would have to be properly accounted for in the study of fast ignition in precompressed degenerate targets.

Degeneracy effects could also be of importance in the propagation of fusion burning waves in highly compressed targets (Chu, 1972; Eliezer & Martinez-Val, 1998) where a double front could develop, because electron heat conduction is not inhibited in degenerate plasmas. The former analysis of bremsstrahlung emission would therefore be relevant in physical cases as the one depicted in Figure 7, where a first wavefront of electron temperature moves ahead of the fusion burning front (at higher ion temperature). In highly compressed targets, the colder fuel could be degenerate and could reabsorb a fraction of the radiation emitted from the reacting zone. It is worth remembering that in the classical case, an optically thick region is given by the condition that the total radiation loss can not exceed the black body radiation limit:

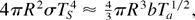
where Ts is the surface temperature and Ta the average volume one, b being a term to characterize the bremsstrahlung emission (including the density factors) and σ the Stefan–Boltzmann constant. If the same temperature is assumed for Ta and Ts (which is an oversimplified hypothesis), it is found for the classical case that the spark radius for which the plasma becomes optically thick is

which is related to the fact that the radiation mean free path in a classical plasma scales as T7/2, assuming thermal equilibrium between electrons and radiation.

Ion and temperature profiles in a double-front fusion burning wave, in a precompressed degenerate target.

For the degenerate case, a similar analysis leads to

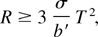
where b′ is the bremsstrahlung parameter for the degenerate formulation. Therefore, in degenerate plasmas, radiation mean free path scales as T2, and it is dominated by bound-free electron transitions in photon absorption, reciprocal to the emission process characterized by Eqs. (9) and (10). Radiation reabsorption could also help the propagation of a fusion burning wave across a plasma highly compressed up to degenerate levels (before the fusion onset), although the main effect will be a dramatic reduction in bremsstrahlung emission.

5. SUMMARY AND CONCLUSIONS

Bremsstrahlung is strongly inhibited in degenerate plasmas, because of the very broad range of electron energy transitions forbidden by Pauli's exclusion principle. The foregoing analysis has shown that actual values for radiation losses decrease very rapidly as the plasma becomes more and more degenerate. In the theoretical case of reaching ultrahigh compressed densities, the actual ignition temperature value would be lower than the classical one. It seems that density levels associated to this phenomenon are beyond the scope of inertial fusion implosions for self-triggered targets. However, bremsstrahlung emission reduction can be important in fast-ignited targets, which can have ignition requirements much lower than those predicted by classical bremsstrahlung models.

References

REFERENCES

Atzeni, S. (1995). Thermonuclear burn performance of volume-ignited and centrally ignited bare deuterium-tritium microspheres. Japan J. Appl. Phys. 43, 1980–1992.Google Scholar
Atzeni, S. (2002). Proc. Inertial Fusion Science and Applications 2001 (Tanaka, K.A., Meyerhofer, D.D. & Meyer-ter-Vehn, J., Eds.), p. 45. Paris: Elsevier.
Azechi, H., Jitsuno, T., Kanabe, T., Katayama, M., Mirna, K., Miyanaga, N., Nakai, M., Nakai, S., Nakaishi, H., Nakatsuka, M., Nishiguchi, A., Norrays, P.A., Setsuhara, Y., Takagi, M., Yamanaka, M. & Yamanaka, C. (1991). High-density compression experiments at ILE. Laser Part. Beams 9, 193–207.Google Scholar
Bodner, S.E. (1981). Critical elements of high gain laser fusion. Fusion Energy 1, 221.Google Scholar
Boreham, B.W., Eliezer, S., Martinez-Val, J.M. et al. (1999). Beam matter interaction physics for fast ignitors. Fusion Eng. Des. 44, 215–224.Google Scholar
Brueckner, K.A. & Jorna, S. (1973). Laser-driven fusion. Rev. Mod. Phys. 46, 325–367.Google Scholar
Chu, M.S. (1972). Thermonuclear reaction waves at high densities. Phys. Fluids 15, 413–422.Google Scholar
Deutsch, C., Furukawa, H., Mima, K., Murakami, M. & Nishihara, K. (1997). Interaction physics of the fast ignitor concept. Laser Part. Beams 15, 557–564.Google Scholar
Eliezer, S., Ghatak, A. & Hora, H. (1986). An Introduction to Equations of State: Theory and Applications. Cambridge, UK: Cambridge University Press.
Eliezer, S. & Martinez-Val, J.M. (1998). Proton-boron-11 fusion reactions induced by heat-detonation burning waves. Laser Part. Beams 16, 581–598.Google Scholar
Kato, Y., Kitagawa, Y., Tanaka, K.A., Kodama, R., Fujita, H., Kanabe, T., Jitsuno, T., Shiraga, H., Takabe, H., Murakami, M., Nishihara, K. & Mima, K. (1997). Plasma Phys. Control Fusion 39, A145–A151.
Key, M.H. (2001). Fast track to fusion energy. Nature 412, 775–776.Google Scholar
Kidder, R.E. (1974). Theory of homogeneous isentropic compression and its application to laser fusion. Nucl. Fusion 14, 53–60.Google Scholar
Kidder, R.E. (1979). Laser-driven isentropic hollow-shell implosions: The problem of ignition. Nucl. Fusion 19, 223–234.Google Scholar
Kodama, R., Norreys, P.A., Mima, K., Dangor, A.E., Evans, R.G. et al. (2001). Fast heating of ultrahigh-density plasma as a step towards laser fusion ignition. Nature 412, 798–802.Google Scholar
Leon, P.T., Eliezer, S., Martinez-Val, J.M. & Piera, M. (2001). Fusion burning waves in degenerate plasmas. Phys. Lett. A 289, 135–140.Google Scholar
Martinez-Val, J.M., Eliezer, S. & Piera, M. (1994). Volume ignition targets for heavy-ion inertial fusion. Laser Part. Beams 12, 681–717.Google Scholar
Maynard, G. & Deutsch, C. (1982). Energy loss and straggling of ions with any velocity in dense plasmas at any temperature. Phys. Rev. A 26, 665–668.Google Scholar
McCrory, R.L., Soures, J.M., Verdon, C.P., Marshall, F.J., Letzring, S.A., Skupsky, S., Kessler, T.J., Kremens, R.L., Knauer, J.P., Kim, H. Delettrez, J., Keck, R.L., &Bradley, D.K. (1988). Laser-driven implosion of thermonuclear fuel to 20 to 40 g cm−3m. Nature 335, 225–229.Google Scholar
Meyer-ter-Vehn, J. (1982). On energy gain of fusion targets: The model of Kidder and Bodner improved. Nucl. Fusion 22, 561–565.Google Scholar
Miyamoto, K. (1980). Plasma Physics for Nuclear Fusion. Cambridge, MA: The MIT Press.
More, R.M. (1993). Nuclear Fusion by Inertial Confinement. Atomic Physics in Dense Plasma (Verlade, G., Ronen, Y. & Martìnez-Val, J.M., Eds.), Boca Raton, FL: CRC Press.
Nakai, S. et al. (1991). Plasma Physics and Controlled Nuclear Fusion Research 1990, IAEA/CN-53/B-1-3, IAEA, Vienna.
Norreys, P.A., Allott, R., Clarke, R.J., Collier, J., Neely, D., Rose, S.J., Zepf, M., Santala, M., Bell, A.R., Krushelnick, K., Dangor, A.E., Woolsey, N.C., Evans, R.G., Habara, H., Norimatsu, T. & Kodama, R. (2000). Experimental studies of the advanced fast ignitor scheme. Phys. Plasmas 7, 3721–3726.Google Scholar
Piriz, A.R. & Sanchez, M.M. (1998). Analytic model for the dynamics of fast ignition. Phys. Plasmas 5, 2721–2726.Google Scholar
Roth, M., Cowan, T.E., Key, M.H., Hatchett, S.P., Brown, C., Fountain, W. Johnson, J., Pennington, D.M., Snavely, R.A., Wilks, S.C., Yasuike, K., Ruhl, H., Pegoraro, F., Bulanov, S.V., Campbell, E.M., Perry, M.D., &Powell, H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436–439.Google Scholar
Skupsky, S. (1977). Energy loss of ions moving through high-density matter. Phys. Rev. A 16, 727–731.Google Scholar
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634.Google Scholar
Tahir, N.A. & Hoffmann, D.H.H. (1994). Development of high gain reduced tritium targets for inertial fusion. Fusion Eng. Des. 24, 413–418.Google Scholar
Totsuji, H. (1985). Bremsstrahlung in high-density plasmas. Phys. Rev. A 32, 3005–3010.Google Scholar
Yaakobi, B., Smalyuk, V.A., Delettrez, J.A., Town, R.P.J., Marshall, F.J., Glebov, V.Yu., Petrasso, R.D., Soures, J.M., Meyerhofer, D.D. & Seka, W. (1999). Spherical implosion experiments on OMEGA: Measurements of the cold, compressed shell. Proc. IFSA 99 Conference, pp. 115–121. Labaune, C., Hogan, W. & Tanaka, K.A. (Eds.) Paris: Elsevier.
Yamanaka, C. et al. (1986). Laser implosion of high-aspect-ratio targets produces thermonuclear neutron yields exceeding 1012 by use of shock multiplexing. Phys. Rev. Lett. 56, 1575–1578.Google Scholar
Yamanaka, C. & Nakai, S. (1986). Thermonuclear neutron yield to 1012 achieved with Gekko XII green laser. Nature 319, 757–759.Google Scholar
Yamanaka, C. et al. (1987). High thermonuclear neutron yields by shock multiplexing implosion with Gekko XII green laser. Nucl. Fusion 27, 19–30.Google Scholar
Figure 0

Integrand of Eq. (10) for a degenerate plasma with εF0 = 3.65 keV and Te = 100 eV. It is observed that the integrand vanishes for all energies except those close to εF0, and for small values of hν. For other electron and photon energies, bremsstrahlung emission is not possible.

Figure 1

Bremsstrahlung emission power from a deuterium–tritium plasma as a function of Te, for various electron densities. Each line shows a low Te range, corresponding to degenerate cases, and a high Te range, for classical plasmas. The fitting between both regimes is very smooth.

Figure 2

Ratio between the bremsstrahlung power of degenerate cases and the power of classical ones, for different temperatures. At temperatures lower than the transition value, the classical formulation is not valid.

Figure 3

Bremsstrahlung spectrum for different cases. Classical plasmas show a straight line in the semilog scale. In the degenerate case, the slope changes for small values of hν.

Figure 4

Ratio of bremsstrahlung spectrum of a degenerate plasma to the spectrum obtained from the formulation of the classical case. The ratio is 1 when the case has a negative η value (classical domain) because the degenerate case formulation tends to the classical one a η → −∞ (for practical purposes, as η ≤ −5).

Figure 5

Bremsstrahlung power and alpha-particle power for stoichiometric deuterium-tritium, as a function of T, for different electron densities. When this one is above 1027 cm−3, the low ignition temperature regime appears.

Figure 6

Ion and temperature profiles in a double-front fusion burning wave, in a precompressed degenerate target.