2. BEAM ELEMENT AND ION SOURCE

Any element with a finite electron affinity (the binding energy of an added electron) can be used to produce negative ions. However, a practical heavy ion fusion source utilizing many merging beamlets will probably require a current density of roughly 100 mA/cm² (Kwan et al., 2001). Although there are many electronegative elements, only the halogens have sufficiently large electron affinities to render current densities of this magnitude likely. Four of the halogens have exceptionally high electron affinities: fluorine (3.45 eV), chlorine (3.61 eV), bromine (3.63 eV), and iodine (3.06 eV). The first two of these exist as diatomic gases at room temperature, and the latter two form diatomic vapors at moderately elevated temperatures. Consequently, it should be relatively straightforward to produce usefully high current densities of negative ions of any of these halogens over large areas with plasma sources similar to those used to produce beams of positive ions. Experience in the semiconductor industry has shown, for instance, that the majority of ion species in chlorine discharges is Cl⁻ at moderate arc power densities and a pressure of 10–20 mtorr (V.M. Donnelley, pers. comm.). Unlike hydrogen, which has an electron affinity of only 0.75 eV, halogens do not require the addition of cesium to augment negative ion production.

Accordingly, properly optimized, the available current densities of these halogens should be similar to positive ion current densities that could be achieved with elements of similar masses. Under these conditions, the current density that can actually be extracted will be determined by the strength of the extraction electric field, which will be a function of the extractor design. Thus, for optimized negative ion sources, the beam current density should be similar to that which would be achieved with a positive ion of similar mass. Since the negative ions are formed by dissociative attachment, the temperature of the negative ions should not be appreciably higher than the temperature for corresponding positive ions, although this will need to be determined by emittance measurements. As is the case with positive ions, the beam rise and fall times will be determined by the speed of the high voltage switching.

Unlike a positive ion source, a negative ion source requires the application of techniques to suppress the coextraction of electrons with the negative ions. In the absence of any electron suppression, the extracted electron current exceeds the negative ion current by the ratio of the mobilities of the two species; for similar temperatures, this is proportional to the square root of their masses, a large number. This is a problem that has been dealt with for years in the realm of high-current negative deuterium ion sources used for magnetic confinement fusion (Kuriyama, 1997). Magnetic fields, which have very little effect on the massive ions, but a large effect on the electrons, along with bias voltages of a few volts between the plasma and the first electrode, can reduce the electron component to a small fraction of the ion current by the time the beam leaves the first extractor stage.

Although bromine, with a mass of 81 amu, and iodine, with a mass of 127 amu, are the most likely candidates for a heavy ion driver, a proof-of-principle experiment could be carried out with fluorine or chlorine, which would be valid models for the heavier halogens because they have similar electron affinities and chemistry. These gases are toxic, but less so than some gaseous feedstocks commonly used in the ion implanter industry.

3. PHOTODETACHMENT NEUTRALIZERS

Although negative ion beams are appealing even if they are not neutralized because they avoid the problem of electron accumulation, which is endemic to positive ions, they could also be converted to atomic neutrals just prior to entering the target chamber by neutralizers that would be a very small part of the overall heavy ion driver system. Hydrogen negative ions can be converted to neutrals in gas cells with efficiencies of 60%, but gas cells result in low efficiencies for heavier negative ions due to the prevalence of multi-electron-loss events (Grisham et al., 1982). Fortunately, photodetachment neutralizers, which were considered long ago for the magnetic confinement fusion beam program (Fink et al., 1979), are well suited to the characteristics of heavy ion driver beams. By choosing a photon energy that is greater than the electron affinity of the beam element, but much less than the ionization energy of the next electron, it should be possible to approach 100% atomic neutralization. Photodetachment neutralizers, which would use intense laser beams in mirrored cells, are best suited to high-power-density, short-pulse beams. These characteristics are much better typified by heavy ion drivers than they were of magnetic confinement heating beams.

Although the database for photodetachment cross sections is limited, the cross section generally rises steeply at photon energies just slightly greater than the binding energy of the extra electron, and then varies weakly with photon energies more than 0.2–0.4 eV above the binding energy. A wavelength shorter than 0.34 μm will be adequate to photodetach any of the halogen negative ions. Two well-developed laser systems, KrF and xenon, are capable of this. According to the Plasma Formulary (2000 edition), the pulsed power levels available in 1990 were in excess of 10⁹ W for KrF lasers, and greater than 10⁸ W for xenon lasers. At that time, the best efficiencies of these lasers were 0.08 for KrF and 0.02 for xenon. Achieving the laser lifetime required for heavy ion drivers may require additional development, since these high-power lasers have not been used for many millions of shots.

Although the amount of laser power required to photodetach an ion beam will depend on many details, such as the beam diameter and spacing and mirror reflectivities, we can examine a simplified example to assess whether existing laser technology is likely to be qualitatively adequate. Consider an I⁻ beam pulse with a 1 cm² cross section and a length of 10 ns. Although we do not currently have data on the cross sections of beams we would like to use, data and calculations for a variety of other negative ions in Massey (1976) show photodetachment cross sections varying in the range of 1 × 10⁻¹⁷ cm² to 2.4 × 10⁻¹⁶ cm². For this example, we choose the bottom of this range, 1 × 10⁻¹⁷ cm². The 4.7-eV photons of a KrF laser should be very suitable for photodetaching I⁻, which is bound by 3.06 eV. The line density (LD) of 4.7 eV photons required to neutralize a fraction n_f of a 4-GeV negative-ion beam of iodine per centimeter of beam width is given by the expression (Grisham, 2003):

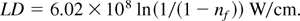
The beam current normally does not appear in photodetachment neutralizer formulas because the ion beam is optically thin. In this example, neutralizing 99% of the beam will require a line density of 2.77 × 10⁹ W/cm. If we use a 20-ns pulse to neutralize a 10-ns ion beam pulse by maintaining this line density across a beam diameter of 3 cm, the required laser energy in a pulse is 166.2 J. With mirrors allowing 100 low-loss reflections, which should be readily available, the energy requirement drops to 1.7 J at a laser power of 2.77 × 10⁷ W/cm. Light travels 6 m in 20 ns, enough time for 150 transits along a 4-cm bounce path. With a laser efficiency of 0.08, the required input power to the laser is 21 J. Although this example is greatly simplified, it does appear that a photodetachment neutralizer should be feasible.

4. BEAM REIONIZATION

At low energies of a few tens of kiloelectron volts per atomic mass unit, the cross sections for stripping a negative ion to a neutral are larger than those for neutralizing a positive ion, so the quality of the vacuum in the immediate vicinity of the source is more important for a negative ion beam. Because the halogen negative ions are more than four times more strongly bound than D⁻, low energy stripping should be less of an issue than it is for deuterium, which is commonly used for large negative ion beams. Moreover, the feedstocks for bromine and iodine, the most probable negative ion drivers, will probably be metal vapors, which can be very quickly pumped. An advantage of negative ions relative to positive ions is that if a negative ion is stripped to a neutral while being extracted from the source, it is unlikely to be converted back to a negative ion through collisions with gas in the initial electrostatic accelerator; thus, a lower energy negative ion tail should not arise, as might happen with positive ions. Having no energy dispersion on the beam going into the main accelerator is a desirable characteristic.

A more serious consideration is the vacuum requirement for the vastly longer path length of the high energy beam through the induction linac, drift-compression region, and final focus optics. As an example, we consider a path length of 1 km, and we take the ionization cross section to be 6 × 10⁻¹⁶ cm². The cross section is an estimate for ionization of Br⁻ at 20 MeV/amu striking molecular nitrogen (I. Kaganovich, pers. comm.), using a model calibrated from the experiments in Mueller et al. (2001). At higher energies, the cross section would decline, reaching about 4 × 10⁻¹⁶ cm² at 40 MeV/amu. To lose less than 0.5% of the beam across a 1-km flight path, the pressure should be no higher than 2.5 × 10⁻⁹ torr. For a system this large, this pressure is probably challenging, but not prohibitive.

In any event, the high-energy vacuum requirement for negative ions should not differ significantly from whatever is determined to be necessary for singly charged positive ion beams. This arises from the observation that at higher energies of 100s of kiloelectron volts per atomic mass unit to 10s of megaelectron volts per atomic mass unit, the positive ions are themselves subject to ionization to higher charge states, with total cross sections that are probably not significantly smaller than for the negative ions. One can see this readily from the fact that the translational kinetic energy of the electrons is larger than the binding energies for most of the electrons in the projectile's electron cloud, not simply the extra electron of the negative ion. For example, at an energy of just 1.4 MeV/amu, the translational kinetic energy of the bound electrons is 0.76 keV.

Beam–beam collisions along the path of an induction linac and the drift-compression region after it can also be a loss term for either positive or negative ions. However, this should be a minor (less than 1%) effect for path lengths of a few kilometers (Grisham, 2003).

Whether there will be additional value in neutralizing the negative ion beam just prior to it entering the target chamber will be depend on the chamber pressure eventually adopted for a reactor. To estimate the target chamber vacuum requirements that would enable an atomic beam to be useful, we consider as an example a 40-MeV/amu bromine beam crossing a 3-m-radius target chamber, with the assumption that the beam total ionization cross section in FLIBE will be about 4 × 10⁻¹⁶ cm², based on a theoretical estimate (I. Kaganovich, pers. comm.) calibrated against the experiments in Mueller et al. (2001). To ionize less than 5% of the neutral beam, in which case space-charge effects would be negligible, the pressure should be no more than 1.3 × 10⁻⁵ torr. This is a stringent requirement, especially for a target chamber with liquid FLIBE walls and jets. The HYLIFE-II (Callahan, 1996) reactor design was expected to have a pressure of 1.7 × 10⁻³ torr of beryllium difluoride vapor. However, recent work suggests that it should be possible to reduce this pressure by factors of 5 (Molvik et al., 2000) or even somewhat more (A.W. Molvik, pers. comm.) by various means, including the use of some lower-temperature FLIBE jets to shield higher-temperature flows, and by other measures with different salt mixtures. Reducing FLIBE temperature, however, causes some reduction in thermal efficiency.

It is not necessary to limit beam stripping to 5% to appreciably improve the beam dynamics within the target chamber. The self-field perveance, a measure of the influence of the space-charge forces on the eventual spot size, scales as the square of the average charge. Moreover, the effect upon the spot size at the target depends on the distance from the target at which the beam becomes ionized; ionization close to the target produces much less spot size growth than ionization near the chamber entrance. In the absence of space-charge neutralization within the target chamber, if the atomically neutral beam became 50% ionized while traversing a target chamber with uniform vapor density (corresponding to a pressure of 1.3 × 10⁻⁴ torr), then the average ionization would be 25%, and the average self-field perveance would be about 5% of what it would have been if the beam had been singly ionized across the entire flight path. This is a qualitative evaluation; a full comparison would need to include the effects of partial space-charge neutralization by electrons from the chamber gas, as well as the ionization of beam by X rays close to the target, where the lever arm on space charge effects is short.