PEIERLS’ RESULTS OF OPTICAL PROPERTIES OF CONDENSED MEDIA

Peierls (Reference Peierls1976) performed a detailed analysis about the momentum of optical radiation in solid materials under the aspects of the numerous theoretical approaches beginning with the Abraham and Minkowski problem about the momentum of the energy density of electromagnetic radiation. A large number of additional considerations had to be compared including the question whether the photons in media moving with a velocity c _M of less than the vacuum speed of light c, may be described by having a mass (Jammer, Reference Jammer1961; Novak, Reference Novak1983). This question could be formulated by Peierls by arriving at the number of the parameter σ in the equation

(1)$$c_{\rm M}/c=\lpar n^{2} -1\rpar [ 1+\lpar n^{2} - 1\rpar {\rm \sigma} \rsqb /n\comma \;$$

where n is the refractive index of the medium. The considerations focussed mostly on the comparison with the results by Landau et al. (Reference Landau and Lifshitz1960), Ginzburg (Reference Ginzburg1973), Gordon (Reference Gordon1973), and Burt et al. (Reference Burt and Peierls1973).

If the medium is a fully ionized plasma, a factor σ = 0 could be concluded (Hora, Reference Hora1974) resulting in a momentum of the photons to be half of that of Abraham and half that of Minkowski. The criterion was that only under this condition, Fresnel formulas for the reflection were resulting. This was rather simplified because it could be presumed that there can be no coherent forces between the particles in fully ionized plasma. The different situation in solids was underlined by Peierls (Reference Peierls1976) that coherence forces can lead to acoustic waves in the solid due to the electromagnetic radiation as a kind of “Cherenkow sound” of an opto-acoustic effect.

The proof of the Peierls factor for dielectrics of σ = 1/5 was established from the fact that electromagnetic waves are equal to electron waves in first order only showing the beating at coherent superposition. In second order, there is a difference (Hora, Reference Hora1960; Carter et al., Reference Carter and Hora1971) with another long wave length beating only for electron waves. After the coherence condition was confirmed for the effect of quantum modulation (Hora, Reference Hora1970), the second order long beating wave length Λ for electron waves was derived by Salat (Reference Salat1970) using the de Broglie wave length for electrons λ_e and ħ = h/2π with Planck's constant h to arrive at

(2)$$\Lambda _{\rm beo}=8{\rm \lambda} _{e}\lpar E_{0}/ \hbar {\rm \omega} \rpar ^{2}=1.6858 \, {\rm cm}\comma \;$$

where E ₀ is the energy of the electrons in the beam (50 keV) and ω is the radian frequency of the crossing laser beam. When Schwarz received the paper of Salat (Reference Salat1970) for refereeing, he immediately used his experiment with very precisely moving the non-luminescent screen and measured this second order beating length, Figure 1 with a wave length

(3)$$\Lambda _{\rm be}=1.73\lpar 0.01\rpar \, {\rm cm}.$$

Fig. 1. Optical emission intensity from the non-luminescent screen (Schwarz et al., Reference Schwarz and Hora1969) for varying the distance D = r between crystal and screen (Schwarz, Reference Schwarz1971). The minima correspond to the long beating wave length according to Eq. (3).

The theoretical value (Eq. (2)) was 3% lower than the measured long beating wave length. The computation was non-relativistic. A relativistic approximation (Van Zandt et al., Reference Van Zandt and Meyer1970) arrived even at a 14% shorter wave length (1.51 cm) than measured putting the measurements of Schwarz (Reference Schwarz1971) very much in doubt. Using an exact derivation with the Dirac equation for the electrons (Hora, Reference Hora1977), the problem was what dielectric response should be applied for the crystals used by Schwarz (Reference Schwarz1971). An initially used dispersion relation led still to a difference with the experiment when using the σ-value of 1/3 in Eq. (1) of Landau et al. (Reference Hora1960) as elaborated by Varshalovich et al. (Reference Varshalovich and Dyakonov1971). But with the result of Peierls (Reference Peierls1976) of σ = 1/5 in Eq. (1) and a refractive index n = 1.58 of the crystal,

(4)$$c_{\rm M}/c=\lpar n^{2} -1\rpar [ 1+\lpar n^{2} - 1\rpar /5\rsqb /n\comma \;$$

the long beating wave length was

(5)$$\Lambda =1.740\, {\rm cm}.$$

This exactly fits with the measurement of Schwarz (Reference Schwarz1971), Figure 1, and is an immediate proof of the correctness of the Peierls (Reference Peierls1976) theory and also showed the very accurate measurement of the motion of the non-luminescent screen by Schwarz.

Apart from the importance of such an effect for applied physics, it needs a clarification what this result of Peierls (confirmed by the effect of quantum modulation) will mean in fundamental optics problems in condensed matter physics (Bae et al., Reference Bae, Okuyama, Aiyuki and Mizuno1993; Scott et al., Reference Scott, O'sullivan and Reiche1996). Peierls put it into doubt whether this effect can be of interesting magnitude, but one at least has to be aware of these problems with the present research of interaction of laser pulses of some femotsecond duration and petawatt and higher power (Bauke et al., Reference Bauke, Klaiber, Yakaboylu, Hatsagortsyan, Arens, Muller and Keitel2013). Irradiation of diamond layers of nanometer thickness showed extreme deviations from usual properties (Steinke et al., Reference Steinke, Hening, Schnürer, Sokollik, Nickles, Jung, Kiefer, Hörlein, Schreiber, Tajima, Yan, Hegelich, Meyer-Ter-Vehn, Sandner and Habs2010) where a laser pulse was completely absorbed after propagation over 2% wavelength thickness. There was no tunnelling etc. and first comparison with dielectric modified nonlinear (ponderomotive) forces (Hora, Reference Hora2012) was only a first step of an explanation and an analysis is yet to be done whether effects as described by Peierls (Reference Peierls1976) are involved.

CONFIRMING OF THE QUANTUM PROPERTY OF THE SCHWARZ-HORA EFFECT

The generalization of the Kapitza-Diract effect with the crossing of electron beams and laser beams leading to the quantum modulation as summarized (Hora et al., Reference Hora, Handel and Hawkes1987) was first performed by filling the crossing area by a medium. As a first step a crystal (Schwarz et al., Reference Schwarz and Hora1969) was used. A modulation of the electron beam was measured with an upshift or downshift of the electron energy by the energy of the laser photons. This was completely reproduced by detailed measurements when using argon molecules as medium in the crossing area (Andrick et al., Reference Andrick and Langhans1978) and repeated in order to measure further details (Weingartshofer et al., Reference Weingartshofer, Holmes, Sagabah and Jin1985). From the beginning, this was related to a quantum condition formulated in 1969 (Schwarz et al., Reference Schwarz and Hora1969) resulting in a correspondence principle for optical interaction with media. This is explained from an evaluation of the measurements of Weingartshofer et al. (Reference Weingartshofer, Holmes, Sagabah and Jin1985) for clarification of the numerous considerations about the nature of the effect (Hora et al., Reference Hora, Handel and Hawkes1987).

The initial paper on the Schwarz-Hora effect included a rather obvious but nevertheless hypothetical theoretical assumption. When the electrons of the beam are moving through the condensed medium (crystal or molecules), how will they interact without resonance with the laser field as if they are free electrons, in a similar way as being in vacuum or in a high temperature plasma? The basis of quantum mechanics was the use of resonance energies (Heisenberg, Reference Heisenberg1925; Dirac, Reference Dirac1925). Or will there be an interaction with the electrons in the medium on a nonlinear non-resonant kind? In the classical case of plasmas, the electrons are picking up oscillations in the laser field, and returning this “quiver energy” when the laser pulse is leaving the particles, independently from any polarization direction. This corresponds to the exact theoretical solution requiring that free electrons in a laser field should not absorb optical energy or received acceleration according to the linear theory. This change drastically by including nonlinear effects (Hora, Reference Hora1988; Evans, Reference Evans1988). Energy from a laser field to free electrons can be transferred by nonlinear mechanisms as it is now well known (Hora et al., Reference Hora, Hoels, Scheid, Wang, Ho, Osmann and Castillo2000) from electron acceleration in laser fields in vacuum. The fact that energy from laser photons is exchanged with the electrons within a medium (Schwarz et al., Reference Schwarz and Hora1969; Andrick et al., Reference Andrick and Langhans1978; Weingartshofer et al., Reference Weingartshofer, Holmes, Sagabah and Jin1985) can only happen by inclusion of nonlinear processes. The electrons in the medium are not free, and assuming that these behave in a similar way as free electrons can be considered only as a hypothetical virtual process. The coherence conditions were fulfilled (Hora, Reference Hora1970).

Such virtual motion is considered similar to that of free electrons. One obtains then a displacement x along the direction of the electric field E of the laser, determined by the laser intensity I for the oscillation and maximum momentum p = m(dx/dt). It was postulated for the quantum modulation that if xp is less than ħ this should be a range of quantum interaction and if larger than ħ it should be classical as known from fully ionized plasmas. The laser intensity I between these two ranges, expressed from the initial formulation (Schwarz et al., Reference Schwarz and Hora1969) is

(6)$$I=I^{\ast}=m{\rm \omega} ^{3}/\lpar 8{\rm \pi} {\rm \alpha} \rpar ={\rm \pi} ^{2}mc^{3}/\lpar {\rm \alpha} {\rm \lambda} ^{3}\rpar \comma \;$$

where α is the fine structure constant, and λ is the laser wave length. Converting Eq. (5) from cgs units to Watts/cm² results for CO₂ lasers in

(7)$$I^{\ast}=1.403\times 10^{9} \, \hbox{W/cm}^{2}.$$

For continuous wave lasers in the experiments, the quantum condition was fulfilled with intensities I < I* within the quantum range for crystals irradiated with argon lasers (Schwarz et al., Reference Schwarz and Hora1969) and for irradiating argon atoms with CO₂ lasers (Andrick et al., Reference Andrick and Langhans1978; Weingartshofer et al., Reference Weingartshofer, Holmes, Sagabah and Jin1985).

It was interesting, to measure the scattering intensity of the modulation effect from the electron spectra by varying the laser intensity. The result following an evaluation (Hora et al., Reference Hora, Handel and Hawkes1987) from Weingartshofer's et al. (Reference Weingartshofer, Holmes, Sagabah and Jin1985) measurements is shown in Figure 2. When plotting the results in Figure 2, one sees the decrease of the scattering intensity with increasing laser intensity I, down to no scattering when reaching the threshold intensity I* of Eq. (7). This is a proof of the correct conditions of Weingartshofer's et al. sophisticated experiments, and of the intensity threshold I* (Hora et al., Reference Hora, Handel and Hawkes1987) with the limit of the quantum range toward the classical range demonstrated for the basic use in the first of these experiments (Schwarz & Hora, Reference Schwarz and Hora1969). A point of interest for the quantum modulation at very high intensities for relativistic conditions by quantum electrodynamic QED studies can be based on the Handel effect (Handel, Reference Handel1975) with the Handel formula for the quantum 1/f noise (Hora et al., Reference Hora, Handel and Hawkes1987). Handel studies the quantum 1/f effect as a nonlinear interaction of the laser radiation with the vacuum with infinite numbers of laser modes as generalized Schwarz-Hora effect for modulating de-coherence.

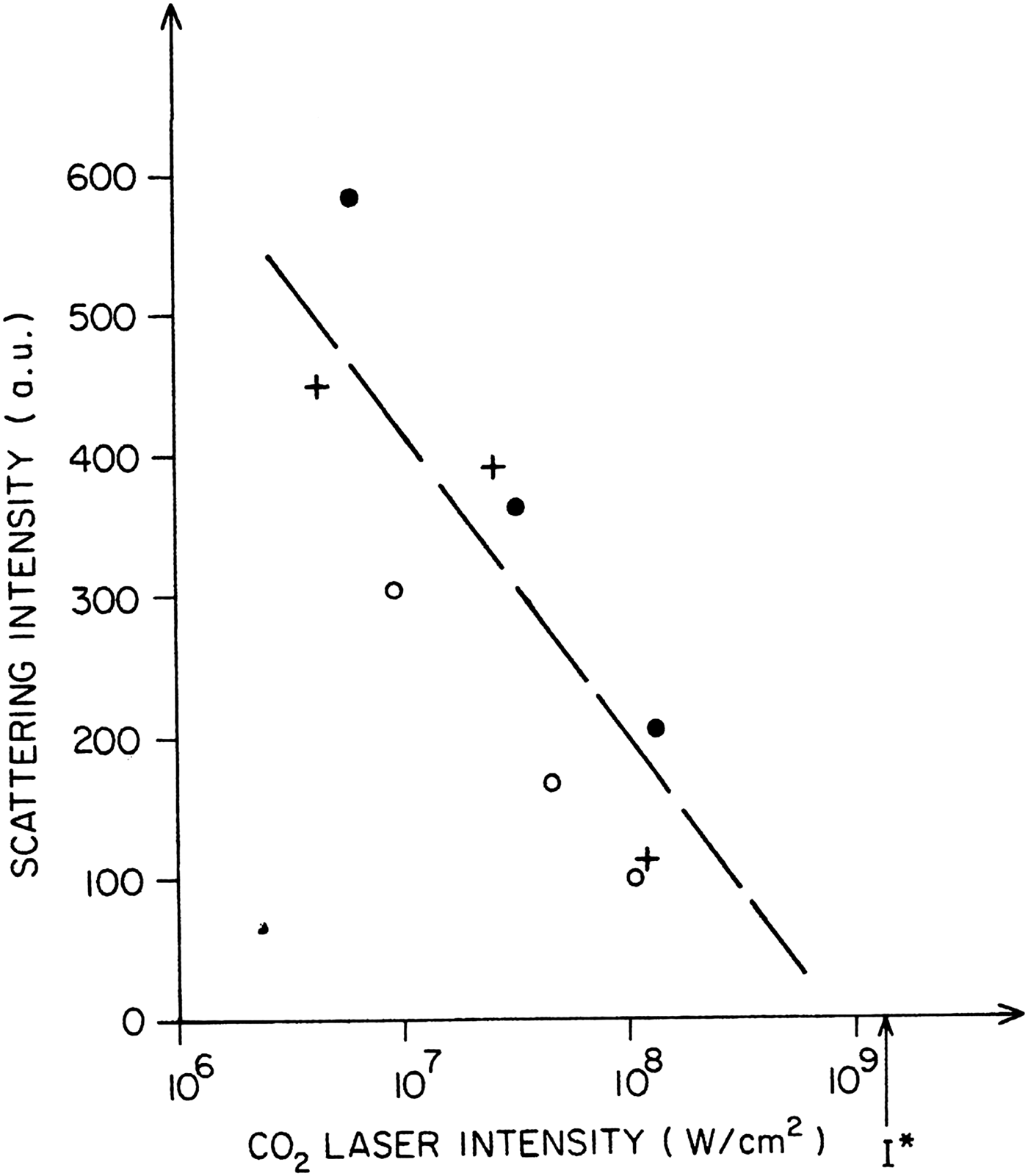
Fig. 2. Measured intensity of the scattered radiation of the electrons (Weingartshofer et al., Reference Weingartshofer, Holmes, Sagabah and Jin1985; evaluated by Hora et al., Reference Hora, Handel and Hawkes1987) on the irradiated CO₂ laser intensity decaying to zero at the threshold intensity I* (Eq. (7)), separating quantum interaction (I < I*) from the classical case (I > I*) defining a correspondence principle for electromagnetic interaction.

SUMMARY

The evaluation of the difference between the very marginal factor σ for the dielectric response of condensed matter to interaction with laser radiation, whether it is 1/3 (Landau et al., Reference Landau and Lifshitz1960) or 1/5 (Peierls, 1973), was not only in a most sophisticated way evaluated by Peierls against the alternatives given by celebrated authorities. It is of fundamental importance for the optics of condensed materials. The presented paper shows a rather special confirmation of the Peierls results from the relation to the recent experimental verification of the Kapitza-Dirac effect (Freimund et al., Reference Freimund, Aflatooni and Batelaan2001) for crossing electron and laser beams in vacuum by generalization for interaction with condensed materials in the crossing area, which led to the quantum modulation of electron beams (Schwarz et al., Reference Schwarz and Hora1969). It is a further example of nonlinear physics in contrast to linear physics (Hora, Reference Hora2000) indicating the non-resonance extension of quantum mechanics by nonlinearity as a point of development (Dirac, Reference Dirac, Hora and Shepanski1978).