2. HOLEBORING IN COLD MATTER

Imagine impinging a laser beam of intensity

onto the critical density of a pre-compressed pellet of local pressure p₀. The laser beam acts like a piston under pressure P_A, which is the sum of the light pressure p_L = (1 + R)I/c, where R is the reflection coefficient and c is the light speed, and the ablation pressure p_A = p_c + ρ_c v_c² = p_c(1 + M_c²); hence, with μ = I/2cp_c,

(Mulser & Bauer, 2004). p_c and M_c are the plasma pressure and Mach number at the critical point. Equation (1) is obtained for a one-dimensional (1D) plasma flow and T_e = const in the evanescent region whose extension, owing to profile steepening, is less than a quarter laser wavelength. Under the action of P_A, a bow shock S traveling at speed v₀ forms (Fig. 1a). In the infinitesimal time dt, the amount of matter ρ₀ v₀ dt undergoes the velocity change from v = 0 to v = v₁, the density change from ρ₀ to ρ₁ and the pressure change from p₀ to p₁ when crossing S. With the compression ratio κ = ρ₁ /ρ₀ holds along the symmetry axis v₁ = v₀(1 − κ⁻¹), and hence, the momentum balance reads

First p_A = n_c kT_e(1 + M_c²) must be evaluated in relation to p_L. The intensity interval of relevance is I = 10¹⁹–10²¹ W cm⁻². The wavelengths considered are λ = 800 nm (Ti:Sa) and λ = 248 nm (KrF). The effective (i.e., relativistic) critical density n_c = γ_eff n_c0 is calculated from formulas given in the literature (Mulser & Bauer, 2004):

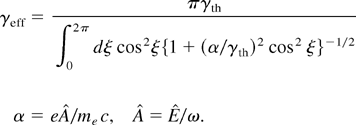
γ_th is defined by Eq. (4). For α/γ_th = 1 results γ_eff = (1 + 0.5)^1/2γ_th, for α/γ_th ≃ 2 follows γ_eff = (1 + 0.8(α/γ_th)²)^1/2γ_th; for (α/γ_th) > 5 γ_eff approaches the asymptotic value γ_eff = 0.785α. This behavior is of great help in preparing Table 1. The relativistic γ-factor used here is considerably different from simple standard expressions generally used.

Holeboring in cold matter: alternative models for matter displacement. a: Laser acts as impermeable piston; PA: piston pressure, ρ0: undisturbed pre-compressed pellet density, v0: hole boring speed. Oblique shock (b) is determined from the shock polar (c). Beyond limiting angle θ shock detaches from cone (d).

Ratio of ablation pressure pA to light pressure pL as a function of laser intensity I

A lower limit of the electron kinetic temperature T_e is obtained from the requirement that under steady-state conditions the absorbed photon flux (1 − R)I must equalize the electron energy flux q_e into the pellet. We set

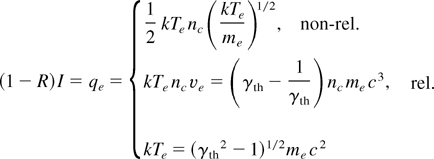
Depending on the divergence of the electron beam q_e, there is an uncertainty factor of order unity in this definition of T_e. For comparison, if in the nonrelativistic expression for q_e an isotropic Maxwellian distribution is used, the correct numerical factor is 2(2/π)^1/2 = 1.6; instead for a collimated, that is, one-dimensional (1D), Maxwellian, it is (2π)^−1/2 = 0.4. For the critical pressure we set p_c = n_c kT_e. In the nonrelativistic case the pressure in one dimension is twice the internal energy 〈E〉, in three dimensions (isotropic) it is two thirds of it, regardless of whether the electron distribution is a Maxwellian or any other distribution. The relativistic case is more complicated. Fortunately it becomes simple again for superrelativistic electrons, that is, q_e = kT_e n_c c if m_e c² << kT_e. Furthermore, in one dimension, p = n〈E〉 and in three dimensions, p = 1/3n〈E〉 holds (e.g., see the photon gas).

In Table 1 n_c0, γ_eff, M_c, T_e, and p_A/p_L are given for the intensities I = 10¹⁹, 2 × 10²⁰, 2 × 10²¹ W cm⁻² and for R = 0.5. An absorption of 50% is a realistic assumption (see, e.g., Feurer et al., 1997; Ruhl et al., 1999). The plasma pressure in the undisturbed pellet before the laser beam arrives is set equal to zero.

From Table 1 important information is extracted regarding the temperature T_e, its dependence on the laser wavelength, and the pressure ratio p_A/p_L. Numerical FI studies do not give much chance to successful ignition for energy flux densities q_e significantly less, for example, by a factor of 3, than q_e = 10²¹ W cm⁻² (Mulser & Bauer, 2004). At Ti:Sa wavelength and 10²¹ W cm⁻² absorbed laser intensity, T_e amounts to 5.3 MeV, even though the relativistic increase of n_c0 is the considerable factor of 20. Because no effect is known so far which would lead to overdense light beam penetration, this temperature is a very reliable lower limit. Unless there occurs very anomalous collective coupling of such energetic electrons to the cold background, the electron beam is not stopped by the pre-compressed pellet and FI fails at λ [gsim ] 1 μm wavelength.

Table 1 underlines the importance of transport and collective deposition research at relativistic intensities. Switching to KrF lasers is a remedy; however it brings T_e down only by a factor of 4 instead of the wavelength ratio squared, that is, 10.4, because with shorter wavelength the relativistic α-factor reduces also and hence γ_eff lowers from γ_eff = 20 to γ_eff = 9. One has to bear in mind that T_e = 1.29 MeV is a lower limit. Future experiments have to show whether absorption takes place at n_c, increasing according to Eq. (3), or whether, due to enormous profile steepening at the critical point, laser beam penetration follows a more modest density increase.

Another important aspect is that the hole boring bow shock always runs into a preheated region of pressure p₀ ≥ p_c because the electron energy transport is faster than v₀. Therefore the maximum effective pressure determining the hole boring speed v₀ is P_A − p₀ = p_L + p_c(1 + M_c²). For all intensities considered in Table 1 P_A − p_c is very close to p_L.

The efficiency of hole boring in a cold background plasma (almost no energy exchange of the electrons from the critical region) may be studied by assuming a pellet density profile of the form ρ₀ = h(x/L)^s. From the pressure balance (2), P_A = fρ₀ v₀² + p_c, f = (1 − κ⁻¹), the depth x/L as a function of t is given by

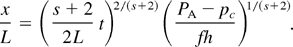
The pressure balance (2) also holds in the absence of a shock, that is, f = 0. Choosing I = 2 × 10²¹, R = 0.5, h = 400 gcm⁻³, t = 20 ps, f = 0.5 (corresponding to κ = 2, typical compression in numerical simulations), L = 0.01 cm and s = 2, one finds with P_A − p_c = 1.5 × 1.05p_L (see Table 1) x/L = 0.45, ρ/h = 0.21, ρ = 83 gcm⁻³. With the exponent s = 3, x/L = 0.53, ρ/h = 0.15, ρ = 59 gcm⁻³. Now a typical “hole boring prepulse,” frequently quoted in the literature, of I = 10¹⁹ W cm⁻², P_A − p_c = 1.5 × 1.2 (Table 1), s = 2, and t = 50 fs is considered: x/L = 0.23, ρ/h = 0.055, ρ = 22 gcm⁻³. After 20 ps, the laser has penetrated up to ρ = 8 gcm⁻³ only. Thus, at such an intensity hole boring is rather modest even in the most favorable case of cold plasma.

There remain some uncertainties originating from the laser pulse transverse intensity distribution and beam width, in the bow-shock model all summarized by the factor f. It is therefore illuminating to use an alternative model that is also accessible to an analytical treatment. As soon as the bow shock invades a density region ρ₀ [gsim ] 1 gcm⁻³ (i.e., 5 times solid DT) the mass flows p_c M_c and ρ₀ v₀ obey the inequality p_c M_c << ρ₀ v₀. As a consequence, there is nearly stagnation on the axis in front of the piston P. This means that the laser acts nearly like an impermeable piston, deviating almost all plasma laterally. Therefore a solid cone-shaped piston of narrow aperture angle θ propagating at speed v₀ is considered. From the vertex of the piston P a coaxial conical shock of aperture angle α originates (Fig. 1b). Under the assumption of negligible pressure p₀, the possible states behind the shock cone (region 1) can be determined from the shock polar, which in Fig. 1c is given for κ = 4. When normalized to v₀ it reads V_y² = (1 − V_x)(V_x − κ⁻¹). From the continuous transition of the tangential component through the shock front, that is, v_0∥ = v_1∥ (see, e.g., any textbook of gas dynamics), one derives

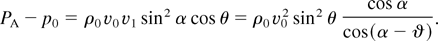
For angles θ such that the straight line starting from the origin does not have any point in common with the shock polar, the shock S forms at a finite distance from the cone with finite curvature on the axis (Fig. 1c), and Eq. (2) applies again. For a strong shock, equivalent to p₀ = 0, the limiting angle is given by tan θ = (κ − 1)/2κ^1/2. For κ = 4 results, tan θ = ¾ and θ = 37°. The corresponding angle α follows from Figure 1, that is, θ = 64°, and the angular factor in Eq. (6), corresponding to the f-factor of Eq. (5), assumes the value 0.32. For the cone and shock angles of θ = 28° and α = 40° indicated in Figure 1, the angular factor is 0.29. The factor decreases monotonically with decreasing aperture angle of the cone and, at given P_A − p₀, v₀ increases. For a strong shock of Figure 1a,c the factor becomes f = 1 − ¼ = 0.75. The comparison of the two models shows that a laser beam with a narrow cone-shaped intensity profile accelerates hole boring owing to an f-factor less than 0.5 in the denominator of Eq. (5): with f = 0.29, x/L increases by a factor of 1.15 (s = 2) and 1.11 (s = 3). The conclusion, also to the authors' surprise, is that even in the most favorable situation of cold matter, that is, collimated hot electrons interacting with the dense pellet core only, hole boring at all relevant laser beam intensities is not very efficient.

3. HOLEBORING IN HOT MATTER

3.2. Analytical considerations

From the ignition condition ρR = 0.3, at ρ = 400 gcm⁻³ a radius R = 7.5 μm results. The energy needed for ignition is typically 15 kJ (Atzeni, 1999; Mulser & Bauer, 2004). Let us now assume that the compressed core is heated by an electron beam of energy flux density q_e through one spot hemisphere during the time τ = 20 ps. The energy balance 2πR²q_eτ = 15 kJ leads to q_e = 2.1 × 10²⁰ W cm⁻². Surprising enough, this value agrees with the hydrodynamic beam calculations without flux limit (Hain & Mulser, 2001; see Fig. 2 therein). The comparison with the ignition energy of 75 kJ when the heat flux limit is introduced shows that in a diffusive model, most of the FI energy is not supplied to the compressed core during the phase of high compression. The location where the flux limit plays its decisive role is the high density jump behind the laser deposition region. To transport the necessary FI energy flux q_e = 2.1 × 10²⁰ W cm⁻² to the compressed core of radius R = 7.5 μm with

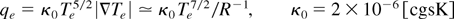
for DT (Z = 1; Braginskii 1966), T_e must be as high as T_e = 34 keV, in good agreement with the numerical simulations.

Direct heating of the pellet core by electrons produced in the critical region requires a mean free path λ_e = (2n_DTσ)⁻¹, where σ is a Coulomb cross section, of the order of 2R. Because the moderately relativistic differential cross section σ_Ω is σ_Ω = γ⁻²σ_R (Sakurai, 1967), where σ_R is the Rutherford cross section, the total cross section σ for momentum transfer is

where λ_D is the Debye length, λ_B is the reduced de Broglie wavelength, and

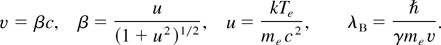
For the ratios u = 1.0, 1.5, and 2.0, m_e c² = 511 keV, the Coulomb logarithms for ρ_DT = 400 gcm⁻³ (corresponding to n_DT = 10²⁶ cm⁻³) and T_e = 40 keV are ln Λ = 5.6, 5.2, and 4.9, and the mean free paths λ_e amount to

Hence, it can be concluded that electrons of kT_e > 1.5 m_e c₂ = 770 keV are not stopped by an ICF pellet of standard dimensions (here: 5 mg mass and ρ_max = 400 gcm⁻³) and direct FI with fast electrons produced by a laser of λ [gsim ] λ_Ti:Sa fails (see Table 1) if binary collisions with cold electrons and ions are the only interaction mechanism. At λ = λ_KrF there seems to exist a possibility for FI on the basis of binary transport mechanisms as considered until now. However, one must be aware of the fact that the estimates for kT_e in Table 1 are minimum values. In addition, numerical FI studies with collimated electron beams show that the required beam energies are closer to 100 than to 10 kJ (Hain, 1999).

Owing to the lack of knowledge on energy transfer from the critical region to the target interior, hole boring can be analyzed only on the basis of more or less reasonable assumptions which, at the same time, are basic enough to allow us to come to valid conclusions.

3.2.1. Flux-limited Spitzer model

It is assumed that the energy transport from the absorption region occurs diffusively. Owing to the low collisionality q_e is nonlocal and strongly inhibited. The evolution of p₀ = n₀ kT_e0 is evaluated for q_e = I(1 − R) = 10²¹ W cm⁻² = const over τ = 20 ps at λ = 248 nm (KrF). In a plasma of constant density, the heat diffusion equation

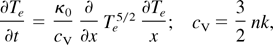
can be integrated for q_e = κ₀T_max^5/2∂Tmax/∂x = const under the approximation 〈T_e〉 = T_max. By observing that q_e = c_V〈T_e〉x_F, a straightforward calculation leads to the evolution of the heat front position x_F(t) as follows:

Interestingly enough, if ∂T_e /∂x is approximated by T_e /x_F(t), an expression for x_F(t) is obtained in which only the numerical factor (9/28)^2/9 = 0.78 is replaced by 1.0 (Zel'dovich & Raizer, 1967). Owing to the strong temperature dependence of q_e, the rectangular temperature profile T(x,t) is approximately preserved (or, at least, remains self-similar) when the plasma is inhomogeneous. By setting, for convenience,

, with

(h, L from (5)),

, and integrating x_F = 7x_F/9t, x_F(t) is deduced for variable specific heat:

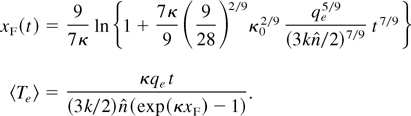
Its derivative

is consistent with

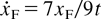
if the second term in the bracket is much larger than 1. This is generally fulfilled except for irrelevant, very short times (t < 2 × 10⁻¹³ s in the following). x_F(t), 〈T_e〉(t), and p₀(t) are evaluated now for q_e = 10²¹ W cm⁻² at KrF wavelength. From Table 1 and Eq. (8), the ratio κλ_e = λ_e /L_c ≃ 10³ is found (λ_e is the electron mean free path, L_c = 1/κ is the scale length at critical density, κ = 640 cm⁻¹) for which, according to Tahraoui and Bendib (2002) a heat flux inhibition factor f_q = 1.2 × 10⁻⁴ results, that is, in (12) κ₀ = 2 × 10⁻⁶ [cgsK] has to be replaced by κ₀ = 2 × 10⁻⁶f_q = 2.4 × 10⁻¹⁰. With these parameters, Table 2 is obtained. In the neighborhood of the critical density the shock wave propagates at a speed v₀ ≃ c/20 if f = 0.5 is set. Thus, the heat wave preheats the undisturbed pellet density creating in this way the counterpressure p₀. From Table 2 it follows that hole boring stops at a time below 0.5 ps at the negligible depth of approximately 4–5 μm.

Thermal wave front xF, electron temperature 〈Te〉, and electron pressure p0 near xF for absorbed laser flux qe = 1021 W cm−2 (KrF)

The hole boring pressure here is P_A ≃ p_L = (1 + R)I/c = 1 Tbar. P_A scales like I, p₀ roughly like αq_e /x_F ∼ I^1/2I^4/9 < I. Owing to the monotonic decrease of f_q with decreasing laser flux density, p₀ ∼ I^δ, with

, hole boring reduces with decreasing intensity of irradiation. Hence, in agreement with the numerical simulation for I [lsim ] 10²¹ W cm⁻², hole boring is suppressed when flux-limited Spitzer–Braginskii-type energy transport takes place. It should be noted that f_q used here (and all similar f_q from the published literature) is strictly valid for electron distribution functions close to equilibrium, a condition which may not be fulfilled at superhigh laser intensities.

3.2.2. Anomalous electron beam stopping

At laser wavelengths of the order of 1 μm (Nd, Ti:Sa, iodine) and beam energies in the multikilojoule range the bulk of the electrons acquires energies too high to be slowed down by a standard-size ICF pellet. The situation may change only if strongly enhanced collective stopping occurs somewhere in the pellet. Fortunately there are indications of such an anomalously intensified energy exchange, from numerical simulations (Ruhl, 2002; Sentoku et al., 2002), as well as from analytical and semianalytical modeling (Das & Kaw, 2001; Jain et al., 2003). Anomalous effects are expected to be bounded to the neighborhood of the critical region and to decay in the more remote dense zones of the pellet owing to collisional damping and the absence of forces driving instabilities to a high saturation level.

The alternative model in this section assumes that the more or less collimated electron jets from Table 1 are subject to collective stopping over a length of perhaps a few tens of microns. According to Das and Kaw (2001) and Jain et al. (2003) a quasilinear friction term ν_eff of the order of

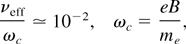
acts on the fast electrons. At intensities I ≃ 10²¹ W cm⁻² a self-generated magnetic field of 1 GGauss, corresponding to an electron cyclotron frequency ω_c = 2 × 10¹⁶ s⁻¹, may be assumed. Hence ν_eff [gsim ] 10¹⁴ s⁻¹ will result and a relativistic electron moving at speed c thermalizes over a few λ_e ≃ 3 μm, typically 3λ_e = 10 μm. On the basis of present understanding this means that Eqs. (12) are applicable with a flux inhibition factor f_q ≃ 10⁻⁴, after thermalization has been achieved, to fluxes q_e = 10²¹ at Ti:Sa laser wavelength too. Owing to the short thermalization time τ < 10⁻¹³ s⁻¹ Table 2 does not change for KrF. For Ti:Sa beams, slightly higher values for x_F, 〈T_e〉, and p₀ are calculated, for example, x_F = 43.6 μm, 〈T_e〉 = 1.7 MeV, p₀ = 2.7 Tbar at t = 5 × 10⁻¹³ s⁻¹.