Introduction
The holy grail of controlled nuclear fusion research, be it by magnetic or inertial plasma confinement, is to find a way to achieve ignition without the energy input from a large nuclear fission explosion. At the present, the only known way to achieve the release of nuclear energy is by the fusion of light atomic nuclei in large thermonuclear explosive devices.
While the realization of nuclear fusion by magnetic confinement is expected to be feasible in the near future, it is unlikely to be possible in compact devices. At the present state of technology, nuclear fusion by lasers is out of reach for lasers, but it may be possible with electric pulse power or by impact fusion. The reason for the rather large energy, more than 50 MJ for ignition, is the Rayleigh–Taylor instability, as was shown by the analysis of Kidder (Reference Kidder and Philips1998).
In this communication, a third possibility is analyzed: the stable implosion of a rapidly rotating target with natural uranium enclosing the fusion fuel, and imploded by intense relativistic electron beams stopped in the dense uranium shell over a distance of a few centimeters. One can for the same purpose also use an ion beam, but this would require a level of intensity and energy that is much more difficult to produce.
In this third way for the achievement of controlled nuclear fusion, the expensive Plutonium 239 “spark plugs” of large thermonuclear explosive devices are replaced with comparatively cheap natural uranium. It can also work with thorium and perhaps even boron 10. Its feasibility is a consequence of Einstein's general theory of relativity, in its importance first recognized by Hund (Reference Hund1948). It is that in a non-inertial reference frame, there can be large actual negative masses, with a negative mass density, which for technically feasible rapid rotation velocities, of the order of ~10 km/s, can be larger than the positive mass density of a neutron star.
This makes it possible to build a cm-size “mass-inverted” virtual miniature neutron star, which as its positive counterpart can be stably imploded.
Kidder's scaling law for the implosion of spherical targets
All laser ignition concepts did not take into account the scaling law for spherical implosion inertial confinement fusion targets by Kidder (Reference Kidder and Philips1998), which is obtained as follows: the energy input for ignition is:
$$E = \displaystyle{1 \over 2}MV_{{\rm imp}}^2 \simeq {\rm \rho} R^3 \simeq \displaystyle{{{(\rm \rho R)}^3} \over {\rm \rho ^2}},$$
where M is the mass of the target and V imp the implosion velocity. For thermonuclear burn in DT, one has 
${\rm \rho} R \sim 1\,{\rm g}/{\rm c}{\rm m}^{\rm 2}$, hence
$$E \simeq \displaystyle{1 \over {\rm \rho ^2}}.$$If R = R 0 is the radius at the beginning of the implosion and R < R 0 the final radius at the end of the implosion, one has,
$$\displaystyle{\rm \rho \over {\rm \rho _0}} = \left( {\displaystyle{{R_0} \over R}} \right)^3,$$and hence
$$E \simeq \left( {\displaystyle{R \over {R_0}}} \right)^6,$$or
$$\displaystyle{{R_0} \over R} \simeq E^{ - 1/6}.$$This means that the ignition energy is very sensitive to the ratio R 0/R, or vice versa, the ratio R 0/R is very insensitive to the energy input and limited to the Rayleigh–Taylor instability (Landau and Lifshitz, Reference Landau and Lifshitz1971). The latest data obtained by the laser implosion experiments of the National Ignition Facility of the Lawrence Livermore National Laboratory have shown no ignition with a laser energy input of 2 MJ. Therefore, raising the laser energy tenfold, from 2 to 20 MJ, would only decrease the ratio R 0/R by the insignificant factor 10−1/6≈0.7. Together with the limitation set by the Rayleigh–Taylor instability, this all but excludes lasers as a means for thermonuclear microexplosion ignition.
The third way
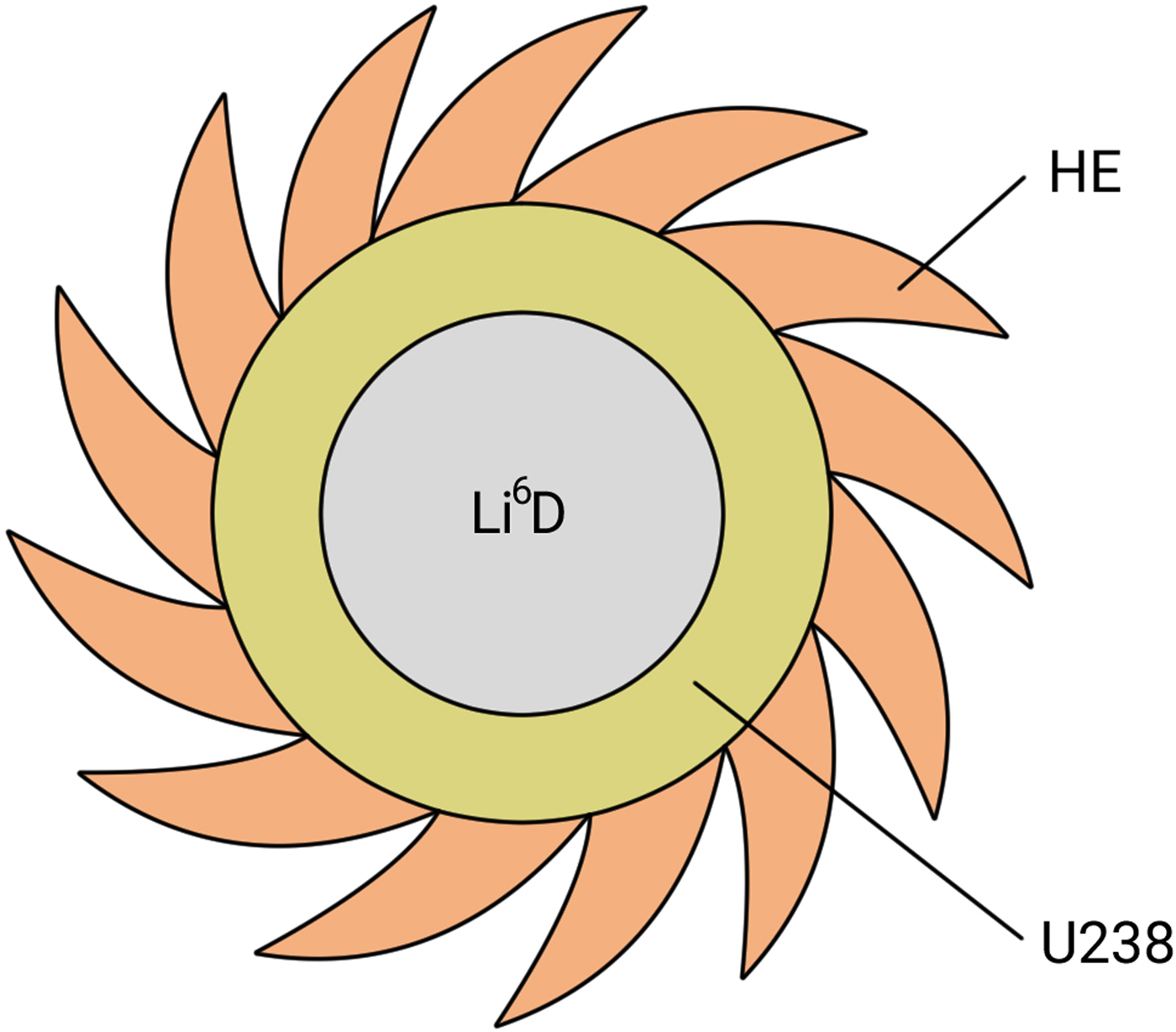
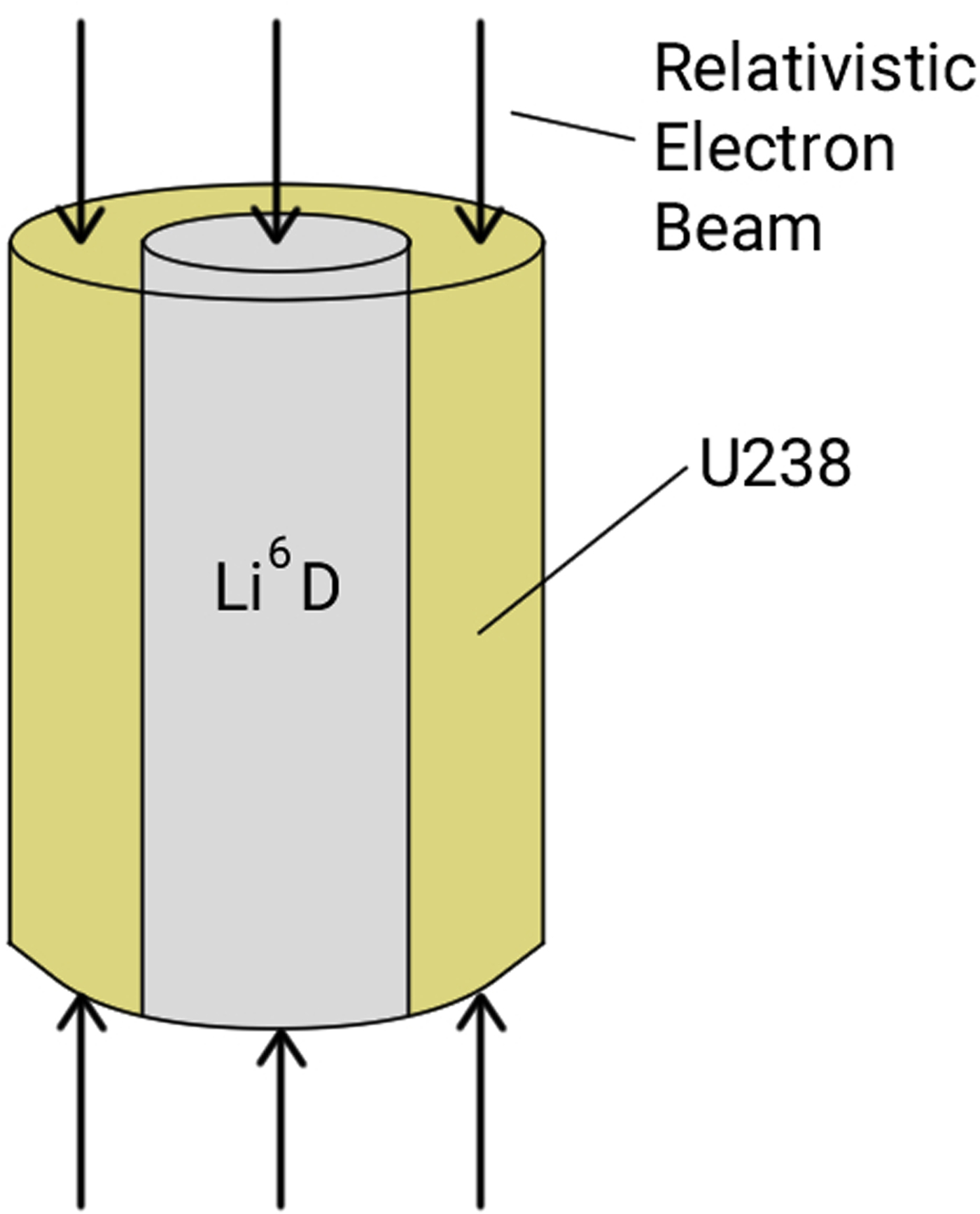
The proposed third way for the controlled release of energy by nuclear fusion is explained in Figures 1 and 2. Figures 1 shows how through the arrangement of chemical high-explosive lenses, a hollowed-out natural uranium cylinder can be brought to a large rotational velocity of the order of 10 km/s. Figure 2 shows how this cylinder can be three-dimensionally imploded by two intense relativistic electron beams projected from above and below the two upper and lower ends of the uranium cylinder.
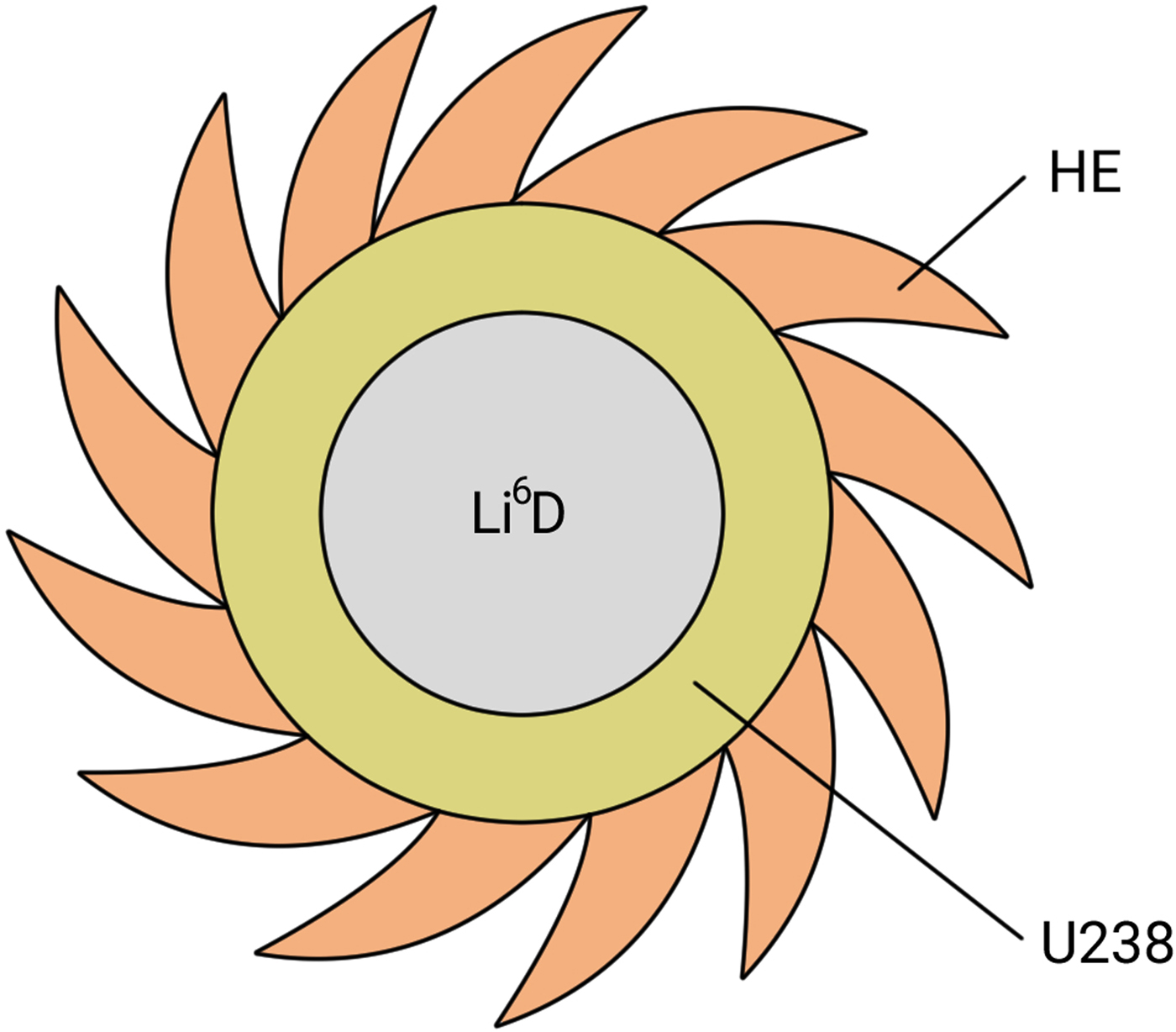
Fig. 1. Arrangement of chemical high-explosive lenses.
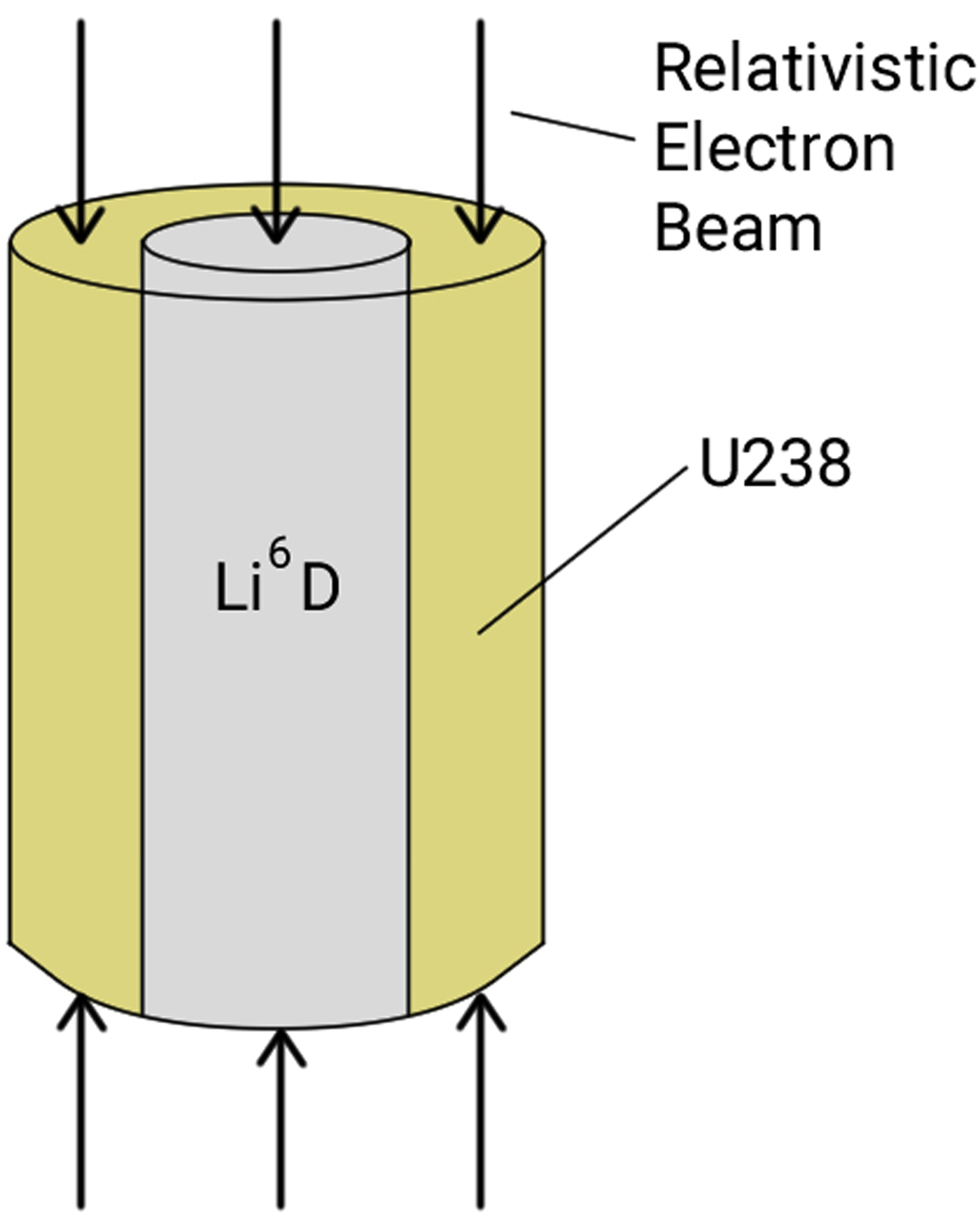
Fig. 2. Uranium cylinder three-dimensionally imploded by two intense relativistic electron beams.
Assuming that the fusion fuel is Li6D salt, as it is used in “dry” H-bombs, the velocity inside the rapidly rotating cylinder is large enough for the chemical decomposition of Li6D into its components, lithium 6 and deuterium. Due to centrifugal forces, the lithium will accumulate at the inner surface of the natural uranium cylinder, while the deuterium will remain in the center. A pulse of relativistic electrons of about 100 MJ dissipated into the uranium shell, will cause the shell, along with the deuterium, to implode it three-dimensionally and ignite a fusion reaction.
The occurrence of the large negative mass densities in the general theory of relativity
While it is not possible to make a laboratory-size star, it is possible to reach a centrifugal field comparable to the gravitational field of a very dense star, with a negative density of the same order of magnitude as the positive density of a neutron star. It is the general theory of relativity (Landau and Lifshitz, Reference Landau and Lifshitz1971) in which the gravitational energy cannot be localized but is described by Einstein's pseudo tensor t ik, the energy and momentum are expressed by a sum of products of Christoffel symbols Γikl, which are the forces. In a non-inertial reference frame, these forces are generally different from zero even in the absence of gravity-producing masses. As it was shown by Hund (Reference Hund1948), for non-relativistic velocities, these forces can be obtained by Newtonian mechanics. In the rotating reference frame inside the rapidly rotating uranium cylinder, the equation of motion for a test particle is given by:
$$m\displaystyle{{d{\bf v}} \over {dt}} = m{\bf F} + m\displaystyle{{\bf v} \over c} \times {\bf C},$$where
$${\bf F} = \; {\rm \omega} ^2{\bf r}$$is the centrifugal force, and
$${\bf C} = \; - 2c{\bf \omega} $$
the Coriolis force, with 
${\bf \omega} $ the angular velocity vector of rotation. If F is a gravitational acceleration produced by the mass distribution of density ρ as the source of Newton's law of gravity, one has:
$$div{\bf F} = \; - 4{\rm \pi} G {\rm \rho}, $$where G is Newton's constant. A centrifugal acceleration is also not free of sources, because of (7) one has
$$div{\bf F} = 2{\rm \omega} ^2$$and hence the negative mass density
$${\rm \rho} = \; - \displaystyle{{\omega ^2} \over {2{\rm \pi} G}}.$$This negative mass is not fictitious and can be felt as the repulsive force in a merry-go-round. For ω = 0.6/s (an example given by Hund), one has ρ = −106 g/cm3, comparable with the positive mass density of a white dwarf star.
The mass density (11) represents a physical reality as the mass density of the electric field E,
$${\rm \rho}_{\rm e} = \displaystyle{{{\bf E}^2} \over {8{\rm \pi} c^2}}.$$While the mass density (12) is positive, because the equal sign charges repel each other, the mass density of a gravitational field g where equal sign masses attract each other, is negative and is
$${\rm \rho}_{\rm g} = - \displaystyle{{{\bf g}^2} \over {8{\rm \pi} Gc^2}}.$$Likewise the mass density of the Coriolis field (8) is
$${\rm \rho} = - \displaystyle{{{\bi C}^2} \over {8{\rm \pi} Gc^2}} = - \displaystyle{{\omega ^2} \over {2{\rm \pi} G}}$$
equal to the mass density given by (11). This means the centrifugal force is caused by the negative mass density of the Coriolis force field. By comparison, the negative mass density –
${\bf F}^2/8{\rm \pi} Gc^2$ of the centrifugal force field (7) is smaller by the order v 2/c 2.
Let us compare the negative mass density with the positive mass density, ρN = 1014g/cm3, of a neutron star. With ω ≃ v/R 0, R 0 ≃ 1 cm is the radius of the target chamber and v ≃ 1 km/s = 105 cm/s, one finds that ω = 2.6 × 105/s and ρ = −1017 g/cm3, three orders of magnitude larger than the positive mass density of a neutron star.
Nernst effect
In the proposed concept, the plasma is confined by the outwardly directed gravitational force of the negative mass of the Coriolis field, and by the inwardly directed magnetic force from the wall of the target chamber, by the Nernst effect.
With the temperature gradient 
$\nabla T$ from the cold wall into the hot deuterium plasma and B the magnetic field, the thermomagnetic current by the Nernst effect is for a hydrogen plasma given by Spitzer (Reference Spitzer1962):
$${\bf j}_{\bf N} = \displaystyle{{3knc} \over {2B^2}}{\bf B} \times \nabla T$$with the magnetic force density of the plasma:
$${\bf f} = \displaystyle{1 \over c}{\bf j}_{\bf N} \times {\bf B} = \displaystyle{{3nk} \over {2B^2}}({\bf B} \times \nabla T) \times {\bf B}$$
or with 
$\nabla T$ perpendicular and B parallel to the wall
$${\bf f} = \displaystyle{3 \over 2}nk\nabla T.$$With the Nernst effect acting like a small magnetohydrodynamic generator, it would only need a small seed-field, equilibrium condition being
$$\nabla p = {\bf f}$$
with 
$p = 2nkT,\; \nabla p = 2nk\nabla T + 2kT\nabla n$, one has
$$2nk\nabla T + 2kT\nabla n = \displaystyle{3 \over 2}nk\nabla T,$$which upon integration yields
$$Tn^4 = {\rm const}.$$In a Cartesian x, y, z coordinate system with the cold wall at z = 0, and the magnetic field B into the x-direction, the Nernst current density j is in the y-direction, and is
$${\bf j}_{\rm y} = - \displaystyle{{3knc} \over {2{\bf B}}}\displaystyle{{dT} \over {dz}}. $$ From Maxwell's equations 
$4{\rm \pi} {\bf j}/{\rm c} = {\rm curl\;} {\bf B}$ one has
$${\bf j}_{\rm y} = \displaystyle{c \over {4{\rm \pi}}} \displaystyle{{d{\bf B}} \over {dz}}.$$ Eliminating 
${\bf j}_{\rm y}$ from (21) and (22) one obtains
$$2{\bf B}\displaystyle{{d{\bf B}} \over {dz}} = - 12{\rm \pi} kn\displaystyle{{dT} \over {dz}}.$$If in the plasma far away from the wall n = n 0, T = T 0, one has from (20)
$$n = \displaystyle{{n_0T_0^{1/4}} \over {T^{1/4}}}.$$Inserting this into (23) one finds
$$d{\bf B}^2 = - \displaystyle{{12{\rm \pi} kn_0T_0^{1/4}} \over {T^{1/4}}}dT.$$With the boundary condition B = B 0 at z = 0 and T = T 0 at z = ∞, integration of (25) yields
$$\displaystyle{{{\bf B}_0^2} \over {8{\rm \pi}}} = 2n_0kT_0.$$ The meaning of (26) is that the magnetic pressure 
${\bf B}_0^2 /8{\rm \pi} $ exerted on the plasma from the wall surface at z = 0, balances the plasma pressure 2n 0kT 0 at z = ∞. With n 0 = 1023/cm3 and T ≃ 108 K, one finds that B 0 ≃ 107 Gauss.
With the Nernst effect, where according to (20) Tn4 = constant, the bremsstrahlung losses going in proportion to 
$n^2\sqrt T $ (Spitzer, Reference Spitzer1962) are constant across the entire plasma, which for nT = constant would rise in proportion to T −3/2. The reason are the large thermomagnetic currents set up in between the hot plasma and the cold wall of the spinning uranium cylinder, leading to a large magnetic force repelling the hot plasma from its wall.
For the working of the Nernst effect one must have
$$\omega \tau \gg 1,$$where ω is the electron cyclotron frequency and τ is the electron–ion collision time. At high magnetic fields of the order B ≃ 107 G and temperatures of the order 108 K, with a particle number density n ≃ 1023/cm3, one has ω ≃ 1014 s−1, τ ≃ 10−9 s (Spitzer, Reference Spitzer1962) and hence ωτ ≃ 105 ≫ 1.
Ignition
The ignition is achieved by a 100 MJ pulse of an intense relativistic electron beam as it was originally proposed by the author (Winterberg, Reference Winterberg1968), except that here the beam stopping does not depend on the two-stream instability, but instead on the classical stopping length. For MeV electrons, the stopping length is determined by the uranium mantle of the target chamber, which implodes the target. The stopping length is given by Winterberg (Reference Winterberg2010):
$$\lambda \simeq \displaystyle{1 \over {\rm \rho}} (0.543 E{ - 0.16})\,{\rm cm,}$$where ρ is the target density in g/cm3 and E is the electron energy in MeV. For ρ≃20 g/cm3 and E≃10 MeV, one obtains λ≃2.6 cm, about equal to the linear dimension of the uranium cylinder.
With 100 MJ 
$ \simeq $ 1015 erg, deposited in a volume 
${\rm V} \simeq {\rm {\rm \pi}} R_0^2 h \gt 25\,{\rm c}{\rm m}^{\rm 3}$, the temperature given by E ≃ nkT, with n ≃ 1023 particles/cm3, is T ≃ 106 K. A threefold implosion of the deuterium increases its temperature by the factor of 100, from T ≃ 106 to T >108 K, meaning it would reach the ignition temperature of the deuterium reaction.
Conclusion
If feasible, the novel thermonuclear fusion concept would have worldwide far-reaching consequences. It could bring an end to the combustion of fossil fuels and minimize the effects of global warming, leaving the fossil fuels for other much more important application in chemistry and medicine.
Unfortunately, the prospect of the much cheaper fission-less ignition of large thermonuclear explosive devises also poses a serious challenge for a world without nuclear weapons.
