Published online by Cambridge University Press: 30 August 2005
We present the current status-of-the-art in Stark broadening theory as a theoretical basis for diagnostics of low temperature plasmas in gas discharges, and of high temperature laser produced or z-pinch dense plasmas. The diagnostics abilities vary depending on the parameters of the gas discharges, or on the range of intensity, and duration of the laser or z-pinch pulses. In the case of high temperature plasmas, besides the conventional diagnostics based on the Stark broadening, the contemporary possibilities of UV and XUV interferometry for plasma density measurements and of tomography reconstruction of the macroscopic gradients of temperature and densities in laser produced plasmas are discussed.
The effect of Stark broadening (SB) in plasmas is one of the most effective tools to determine dense plasma properties experimentally, especially for beam plasma interaction experiments with intense beams of photons and particles (Loboda et al., 2000; Politov et al., 2000; Magunov et al., 2003; Hasegawa et al., 2003; Ying et al., 2003). It is associated with the idea that electric microfield acting on the test particles is the sum of all the electric fields created by the perturbing ions, in the scale of distances at which the quasi-neutrality condition is not fulfilled (see Demura & Gilles, 2004). Hydrogen-like and helium-like lines are the most sensitive to SB, but for practical reasons, we restricted our discussion to hydrogen-like lines. The Stark effect is also responsible for the splitting of spectral lines in several components. The SB of Hydrogen-like lines were proposed for diagnostic of the plasma density after the pioneer work of Holtsmark (1919), where only the Coulomb electric fields of point ions were considered and assumed to be random and static. The half width of the Stark broadened line is determined by the microfield probability distribution function (PDF). The first tabulation of the Stark profiles of the hydrogen spectral line was done by Underhill and Waddell (1959) in the quasi-static approximation for ions with the help of Holtsmark PDF, while the SB by electrons was neglected. Later this simple concept was developed in order to take into account (1) the two types of charged particles in plasma-ions and electrons; (2) the microfield time dependence; (3) the microfield non-uniformity which is connected to the departure from the dipole approximation of the interaction potential between the radiator and the plasma particles; and other specific effects connected to each experimental cases. The introduction of the impact and quasi-static approximations (Griem, 1974) was the simplest of indirectly accounting for the time microfield dependence. This approach, when the SB by electrons is described in the impact approximation while the SB by ions, in the quasi-static approximation with the help of PDF, was reflected in the hydrogen lines tables (Kepple & Griem, 1968), named thereafter KG68. However, the transition of the SB by electrons from the impact to the quasi-static regime in the wings of spectral lines was neglected in the KG68 approach. This transition was described in the frame of the so-called unified theory using the one electron approximation in Vidal et al. (1973), named thereafter VCS73. The corresponding tables Stark profiles of Hydrogen lines are presented in VCS73.
The common starting point for the calculation of the line shapes begins with the Fourier transform of the average Liouville evolution operator U(t). The radiation intensity of the optical transition between two groups of atomic levels, denoted by i, i′, and f, f′, is given by
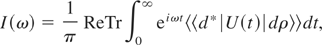
where d and ρ are the dipole and the density matrix operators for the system. For the last quantity, one usually chooses the diagonal equilibrium density matrix operator ρ0 for the unperturbed system (that is, without the effects of the surrounding plasma charges). The average trace is taken over the free atom (or ion) Liouville states contributing to the optical transition. As the initial eigenstates i, i′ of the optical transition are very close in energy, then the diagonal equilibrium density operator may be considered as constant and deleted in Eq. (1). In the quasi-static approximation for the ions and impact approximation for the electrons, the plasma average in Eq. (1) is expressed in terms of ion probability field distribution W (F). Using now for the calculation of the eigenstates of the radiator, perturbed by the constant field F, and assuming for simplicity that the impact operator φ is diagonal, the intensity could be expressed as:
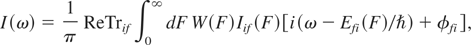
where Iif is the individual component intensity from i to f and Efi = Ef − Ei is the transition energy. The first more general description of SB in terms of time dependent microfields was given in the frames of the model microfield method (MMM) (Frisch & Brissaud, 1971; Brissaud et al., 1976). This model recovers the quasi-static and impact limits of SB by electrons (Stehlé, 1990).
The aim of this paper is to summarize the present status in SB theory in plasmas as a basis of the electronic density diagnostics. We start with the case of low temperature and low density gas discharges, where SB is widely used as a diagnostics, and performances, which can be obtained in these plasmas. Then we present the experimental constraints for high density plasmas and the SB possibilities in these more complex situations. We will also focus on ICF plasmas obtained on lasers or Z pinches facilities (Woolsey et al., 1997; Stygar et al., 2004; Bailey et al., 2004). However, it is important to check SB theoretical predictions in some experiments where other diagnostic can simultaneously provides determination of density. In this context, the contemporary abilities of the UV and X-ray plasma interferometry are very promising (Hammarsten et al., 2004; Zeitoun et al., 2004). The SB diagnostic is also a part of more complicated methods such as polarization spectroscopy (Fujimoto & Kazansky, 1997; Hakel et al., 2004), magnetic polarizer (Mathys et al., 2000), and absorption and fluorescence spectroscopy (Gouveia et al., 2003; Regan et al., 2002; Chambers et al., 2002; Rosmej et al., 2003).
In this section, we present the application of SB to plasmas with electron temperature Te ∼ 1 eV and plasma electron density Ne ∼ 1018 cm−3. Many experimental devices are concerned: plasma torches, discharges, laser induced plasmas, and inductively coupled plasmas. Such plasmas are mostly quiet, uniform, and with long time duration. This allows an accurate spectroscopic measurement of Hydrogen lines. Besides that, electronic density may be measured independently by laser interferometry, allowing a validation of the theories and their further use as an autonomous diagnostic.
A major step of improvement was achieved with the inclusion of ion dynamics in the line broadening theories, starting with the MMM theory. MMM (Seidel, 1977) first gave the order of magnitude of the neutral hydrogen Lyman-α half width measured in the stabilized arcs (Grützmacher & Wende, 1977), with a value 2.5 times larger than KG68 and VCS73 ones! The recent extensive MMM tables are available in Stehlé & Hutcheon (1999).
The first direct computer simulation of SB in the time dependent microfield was performed in the approximation of the straight classical trajectories of the perturbing particles. This model, hereafter called computer simulation along straight trajectories (CSST), gives in principle a better description of ion dynamics than MMM. The CSST tables for the corresponding Hydrogen lines are presented in Gigosos and Cardenoso (1996), and for the recent developments with the joint simulations of the ion and electron microfields (Gigosos et al., 2003). However, the CCST model neglects correlations between “field” particles, important for high density, in principle, are included in MMM. On the basis of KG68, VCS73, MMM, and CSST theories, comparison of the measured and the calculated Stark profiles of hydrogen lines yields an accuracy better than 20% for the density determined for uniform isotropic low temperature plasma of gas discharges without self-absorption. The recent comparison of the full Balmer Stark profiles of Hα, Hβ, and Hγ given by experiment and by MMM and VCS73 is shown in Figure 1 (Acon, B.W., Stehlé, C. & Montaser, A., 2004, private communication). Using the full line shapes, the electronic densities are determined to be, respectively (in cm−3): 3.0 × 1013 (3.5 × 1014) for Hα, 4.9 × 1013 (3.9 × 1013), for Hβ, 3.7 × 1013 (4.0 × 1013) for Hγ using MMM and VCS (in brackets). The measurements were made in plasma torch inductively coupled plasma (ICP) radio-frequency discharge (Cai et al., 1994). MMM computations were performed with Te = Ti = 10000 K.

Best fit of theoretical profiles compared to experimental profiles of Balmer lines recorded in an Helium ICP collected with a high-resolution Fourier transform spectrometer.
These theories are based on standard linear Stark effect, connected to dipole approximation. This linear effect gives the dominant contributions to the line shapes. But spectral line shifts (Nguyen et al., 1986; Koenig et al., 1988), quadrupole and higher order field effects start to affect the line shape at densities larger than 1017 cm−3. In dense plasmas the dipole approximation becomes insufficient to describe the interaction of the field particles with the radiator. However, the non-dipole interaction may be considered as a perturbation, so the problem can be solved in terms of the joint distribution function of microfield and its spatial derivatives (Demura & Sholin, 1975; Demura et al., 1995; Stehlé et al., 2000). Moreover, the MMM as the current CSST codes neglect the effects of the radiator motion using so-called μ-model, that considers only the radiator-perturbed relative motion operating with the reduced mass μ of this pair. The investigation of the effects of the radiator motion also could be done in some special versions of CSST. Although the inclusion of the radiator motion leads to the appearance of several qualitative effects, its overall influence on the Stark profile was found to be negligible.
Beside MMM, there are other indirect models for description of ion dynamics effects such as the frequency fluctuation model (FFM) (Talin et al., 1995) and the frequency separation model (FST) (Alexiou et al., 1997), that in fact are complementary to each other. As they are mostly used for ionic emitters, we present them in more details in the following section. The joint microfield distribution at the neutral or the charged points were recently studied in the Molecular Dynamics simulations of ions and electrons, which allows consider strongly coupled plasmas and the influence of the perturber-perturber correlations (Talin et al., 2003; Ferri et al., 2004). The Molecular Dynamics allows as well testing directly the applicability of μ-model in the ion dynamics depending on the plasma parameters.
All these lines may be and are already used for plasma diagnostic. Among them, the Hβ is relatively insensitive to the ion dynamics (except for the line center dip). Thus, this line may be considered as a corner stone for the diagnostic of low temperature plasmas. The use of the line shape in the near line wings (Acon et al., 2001) allows the more precise determination of the electron density than using the half width value which is more sensitive to the continuum determination in the case of broad lines.
In this section, we will consider plasmas of mid-atomic number (10 < Z < 36) obtained in high power installations (lasers or z-pinches), and more precisely having temperatures at least several hundred eV and densities around or larger than 1021 cm−3. We also focused on Hydrogen and Helium lines.
The theoretical context for Stark profiles of the lines of Hydrogen-like ions is quite similar to the case of Hydrogen lines in low density plasmas. Among previous works summarizing the subject of X-ray spectroscopy application to laser targets and pinch plasmas it is worthy to refer to Boiko et al. (1980). The first scaling analysis of SB application for diagnostics of laser plasmas with highly charged ions was performed by Vinogradov et al. (1974) using the impact and quasi-static broadens approximations. Molecular dynamics simulations have shown later (Langer et al., 2003) that spectral line width of impurities in mixture—used to trace the plasma parameters—are dramatically increased by ion dynamics (Stamm et al., 1986) for typical laser plasmas conditions. The importance of ion dynamics is quite large for lines like Lyα and Heα, but remains negligible for Lyβ and Heβ lines, if one excludes the dip in the line center. The MMM and FFM are alternative methods to describe this effect. Although there are remarkable examples of spectra generated in the frames of FFM that fit well experimental data, it should be kept in mind that FFM operates with the artificial set of two level subsystems adjusted to fit the real static spectrum of the radiating system. The ion dynamics effects are modeled within FFM with an additional parameter—the mixing frequency which artificially couples the microfield substates. This frequency is a constant in FFM, independent of the microfield, contrarily to the MMM frequency jump. Thus, the transition region, which occurs in the line centre between the impact approximation and the quasi-static approximation, has a different variation with density and temperature. Furthermore, a constant mixing frequency prevents FFM from converging toward the quasi-static limit in the far line wings. This shortcoming is not found in the sophisticated kinetic method for charged radiators (Boercker et al., 1987) where the mixing frequency is a function of the detuning from the line center. This theory, formulated for the one component plasma model, couples the plasma microfield statistics and the radiating ion velocity, and set the time integral of the field autocorrelation function to zero. It should be noted, that unlike the MMM, the FFM code could not be reproduced in this paper.
In ICF plasmas and in some other experiments, radiating impurities are introduced in the target for diagnostic purpose. In this case, the line shapes are sensitive to the plasma composition. This sensitivity is a consequence of both plasma ion dynamics and statistics effects in the field distribution functions (Iglesias et al., 2000). They were demonstrated using Monte Carlo (Gilles, 1990; Potekhin et al., 2002) and MMM methods (Gilles & Stehlé, 1994, 1995). However, this effect is relatively small for the Lyβ and Heβ lines.
Another subtle effects is found when initial and final atomic levels are mixed by the plasma microfield and the non-diagonal elements of the density matrix (Eq. 1) has to be included in the calculation of the line profile, which means that SB entangles with kinetics (Anufrienko et al., 1993; Kosarev et al., 1997), in contrast to the usual assumption of a diagonal density matrix in SB (Griem, 1974). These phenomena are known in laser physics as the nonlinear interference effects (NIEF) (Rautian & Shalagin, 1991). It was found that the NIEF also strongly influences the X-ray lasers kinetics (Gasparian et al., 1994). This may be generally neglected in a first approximation.
In strongly coupled plasmas, elegant molecular models were formulated to study the possibility of the formation of two-center (or molecular) transient configurations leading to the apparition of quasi-molecular satellites in the near line wings of Hydrogen-like ions (Leboucher-Dalimier et al., 2001). However, experimentally these observations are extremely difficult to perform. Note also that small dips in the line wings can be generated by intense plasma waves such as those produced by the laser field (Oks, 1995).
More important are the effects of gradients of the microfields (Stehlé et al., 2000) and of quadrupole and higher order field (Kilcrease et al., 1993), which increase with density and lead to line asymmetries and line merging (Inglis & Teller, 1939). Among the 1s-np and 1 s2–1 s-np series of the Hydrogen- and Helium-like ions, the Lyβ and Heβ lines are only slightly affected by these perturbations, but still intense and thus well suited for diagnostic purpose.
For highly charged ions, SB presents other concerns, such as line shifts due to electron collisions (Nguyen et al., 1986; Koenig et al., 1988; Renner et al., 2003). As integration along the line of sight includes different densities to which these shift are dependent, and can lead to apparent broadened and asymmetric profile. But regretfully, the various theoretical approaches differ considerably in the predicted shift values and their functional dependences on plasma parameters. In the absence of validated theories, the analytical expression of Nguyen et al. (1986) may be considered as a possible starting point.
One other difficulty, which is not directly related to the SB theory, is the contribution from the resolved and unresolved dielectronic satellites (as for example the Lyβ satellites 1s nl–3p nl), that inevitably transform the observable SB pattern in the red wing. The deconvolution of the satellites and the red wing would require a full processing for the population balance of the doubly and singly excited states. Thus analysis of the red wing profile of the parent lines may not provide an independent density measurement.
SB of dielectronic satellites from “hollow ions,” which do not overlap with the parent line, were studied in details (Rosmej et al., 2003). Suitable for temperature diagnostic through their intensities, these lines appear not to be suitable for density determination.
We will discuss now the experimental context. Laser produced plasmas are characterized by noticeable non-stationary, non-uniformity, and as a rule, large departure from LTE ionization equilibrium (Busquet et al., 2003). This brings out complex interpretation of the observations, as probing one density and one temperature will never be achieved and time-resolved tomographic reconstruction is extremely difficult due to the small size of the rapidly varying plasma. However, an impressive reconstruction of temperatures (and densities in a lower extent) of an indirect drive target on the OMEGA laser was performed (Welser et al., 2003) under few simplifying assumptions (such as isotropy or monotonic gradient, see Golovkin et al. (2002). A 1280 pinhole array associated with a flat multi-layered Bragg mirror provides monochromatic image (75 eV bandwidth) for each parent lines and their satellites. Genetic algorithm acting on the recorded intensities is used to set a few parameters describing the density and temperature profiles. The collisional radioactive model used for this reconstruction includes satellites, radioactive transport, and Stark profiles. SB is also used to add constraints on density from the time integrated spectrum, see Figures 3 and 5 in Welser et al. (2003). This deconvolution starts from detailed observed data and derives hydrodynamical quantities. In fact, analysis of the experiment would require as a complement to start from hydrodynamical code and through atomic modeling, radioactive transfer and line profile create synthetic spectral data.
In conclusion, in case of high temperature plasmas, we recommend to use of the blue wing of Heβ or Lyβ lines in order to minimize ion dynamics effects, and avoid unresolved satellites. A quasi-static approach of the line shape will be a good first description. An accurate subtraction of the pseudo continuum is necessary, as it will cancel part of the observed asymmetry.
In summary, Stark broadening is widely used as a density diagnostic in low and high temperature plasma in various experimental settings. Improvement of the underlying theory is still in progress regarding line shift by electronic collisions, dielectronic satellites…. High resolution in space, time and spectra (possibly all at the same time!) will obviously allow better determination of local density and temperature. The deconvolution of the experimental spectra emitted by dense plasmas will benefit from post-processing by a full time-dependent collisional-radioactive model (CRM)—including radiation transfer—of a reliable hydrodynamic simulation (Busquet et al., 2004). Thus this CRM may require including NIEF (Anufrienko et al., 1993; Kosarev et al., 1997). In the recent experimental studies of dense laser plasmas, the SB diagnostics is used simultaneously with other density diagnostics in order to perform cross check on the plasma parameters as it was done for the classical studies of the gas discharge plasmas. In this respect the current development of the UV and X-ray interferometry is very appealing for increasing reliability of the SB diagnostic.
The authors are indebted to B.W. Acon for providing the set of hydrogen data and for helpful suggestions. C. Stehlé acknowledges the support of Comité National Français d'Astronomie.

Best fit of theoretical profiles compared to experimental profiles of Balmer lines recorded in an Helium ICP collected with a high-resolution Fourier transform spectrometer.