1. INTRODUCTION
The interaction of fast heavy ions with matter is a unique method to investigate processes in complex atomic systems, which play a very important role in modern atomic physics (Kawamura et al., Reference Kawamura, Horioka and Koike2006; Nardi et al., Reference Nardi, Fisher, Roth, Blazevic and Hoffmann2006). The current research in this field of science is motivated by the application of ion beams for well-tailored energy deposition in matter: inertial fusion, matter heating and tumor therapy (Labaune et al., Reference Labaune, Hogan and Tanaka2000; Hoffmann et al., Reference Hoffmann, Fortov, Lomonosov, Mintsev, Tahir, Varentsov and Wieser2002, Reference Hoffmann, Blazevic, Ni, Rosmej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005; Deutsch & Popoff, Reference Deutsch and Popoff2006; Kraft, Reference Kraft2000).
The applications mentioned above require a detailed and precise knowledge of the energy deposition profiles as a function of projectile energy and the ion stopping range in the material. The target material can be either in solid, gas, liquid, or plasma state; also porous materials are a now days of considerable interest. It was demonstrated that the environment influences the energy deposition process (Nardi et al., Reference Nardi, Maron and Hoffmann2007; Barriga-Carrasco & Maynard, Reference Barriga-Carrasco and Maynard2005; Hoffmann et al., Reference Hoffmann, Jacoby, Laux, Demagistris, Boggasch, Spiller, Stockl, Tauschwitz, Weyrich, Chabot and Gardes1994). An enhanced energy loss and increased charge state of the projectiles was measured in experiments with plasma targets (Hoffmann et al., Reference Hoffmann, Bock, Faenov, Funk, Geissel, Neuner, Pikuz, Rosmej, Roth, Süß, Tahir and Tauschwitz2000; Dietrich et al., Reference Dietrich, Hoffmann, Boggasch, Jacoby, Wahl, Elfers, Haas, Dubenkov and Golubev1992).
Since the ion energy loss of heavy ions in matter is approximately proportional to the square of the ion mean charge, the knowledge about the dependency of the ion charge on the target material properties is of great importance. The first quantitative data about the difference in the charge state distribution of ions emerging from solid and gaseous targets were given by Lassen (Reference Lassen1951a). His experimental work with uranium fission fragments clearly showed that the charge of projectiles emerging from thin carbon foils is higher than the charge of ions emerging from gases. He also found that the charge of ions emerging from gas increases with gas pressure increasing (Lassen, Reference Lassen1951b).
Bohr and Lindhard (Reference Bohr and Lindhard1954) attempted to explain these experimental results (BL model). They related the observed gas-solid difference to the influence of the projectile excited states, which are highly populated if the projectile passes a solid target. Due to the difference in the binding energy of the ground and excited states, the effective ionization rates become higher, and thus lead to the increase of the ion charge state in dense stopping medium. At low target densities, collisional excitation of projectile electronic subshells will disappear due to spontaneous radiative transitions in the ion ground state before the next collision and ionization occur mostly from the ground state.
The BL model was verified experimentally for the high ion energy region. A detailed study was carried out at the accelerator facility UNILAC/GSI (Darmstadt) using krypton, xenon, lead, and uranium projectiles in the energy range of 1–10 MeV/u (Geissel et al., Reference Geissel, Laichter, Schneider and Armbruster1982). It was observed for the first time in experiments with 3.6–7.9 MeV/u uranium projectiles that the stopping power in gases is lower by up to about 20% than in solids.
The new experimental results on the increase of the effective ionization cross-section of 200 MeV/u nickel ions penetrating carbon foils were reported by Ogawa et al. (Reference Ogawa, Geissel, Fettouhi, Fritzsche, Pottillo, Scheidenberger, Shevelko, Surzhykov, Weick, Becker, Boutin, Kindler, Knöbel, Kurcewicz, Litvinov, Lommel, Münzenberg, Plaß, Sakamoto, Stadlmann, Tsuchida, Winkler and Yao2007). The high energy was chosen in order to have simple systems, which are easier to treat theoretically. At this high energy only two nickel charge states with Z = 28+ and 27+ survive at the level of some percent. The charge state distribution of nickel ions after interaction with a carbon foil and a nitrogen gaseous target was compared to each other. A 40% increase of the H-like fraction was detected and attributed to the increase of the total ionization rate in the solid material due to the high ionization cross section of the excited states.
In order to simplify the description of the ion electronic subshells in the stopping process, first theoretical works considered ions carrying only one or two bound electrons. Anholt formulated the four-state model of the population of bare and H-like ions via electron capture, ionization and excitation in collisions with target atoms (Anholt et al., Reference Anholt, Meyerhof, Stoller, Morenzoni, Andriamonje, Molitoris, Baker, Hoffmann, Bowman, Xu, Xu, Frankel, Murphy, Crowe and Rasmussen1984; Anholt, Reference Anholt1985). A simpler three-state model containing 1s, 2s, and 2p levels was solved by Anholt analytically. Calculations have shown that 19% of 400 MeV/u neon projectiles penetrating a Cu-target were excited to the 2s and 2p state. This has caused 30% of the gas-solid charge state difference. The influence of excited states of the projectile on the charge state of relativistic heavy ions was clearly demonstrated.
The strong influence of the projectile excited states on the ion charge state distribution in solid targets has been demonstrated by Rozet et al. (Reference Rozet, Stephan and Vernhet1996). The computer program ETACHE was developed to calculate the charge state distribution of ions with low Z, where electrons distributed over n = 1, 2, and 3 subshells, and for MeV/u projectile energies. The model predictions were in good agreement with experimental measurements for 13.6 MeV/u argon ions in carbon targets. Since the values of the radiative decay rates were introduced not directly but via fluorescence factors with insufficient accuracy, the model is restricted to solid density conditions and to projectiles with low atomic numbers, for which a de-excitation in solids occurs mostly nonradiatively.
The target density effect in collisions of fast ions with solid targets was analyzed in a series of papers by Shevelko et al. (Reference Shevelko, Rosmej, Tawara and Toltikhina2004, Reference Shevelko, Tawara, Ivanov, Miyoshi, Noda, Sato, Subbotin and Tolstikhina2005). There, the target-density dependent formulas for electron capture and projectile ionization were obtained. It was shown that with the target density increasing electron capture cross-sections decrease and ionization cross-sections increase, resulting in a higher mean charge of exit ions after a solid target compared to a gas target. Using this treatment, a good agreement with experimental data on equilibrium charge-state fractions for projectile ions with atomic number Z = 6–26 passing through carbon foils was achieved in the MeV/u energy range.
In the present paper, we demonstrate the numerical calculations of the electronic subshell structure of calcium ions having been slowed down in SiO2 media of different volume densities. These calculations were carried out in order to analyze experimental results for the dependence of the calcium projectiles K-shell radiation on the density of the stopping medium (Rosmej et al., Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a).
2. EXPERIMENT
2.1. Experimental Method
In order to analyze the projectile ion charge and velocity dynamics along the ion stopping path in the target, a novel diagnostic method, spatially resolved X-ray spectroscopy of the K-shell projectile radiation, has been applied (Rosmej et al., Reference Rosmej, Wieser, Geissel, Rosmej, Blazevic, Jacoby, Dewald, Roth, Brambrink, Weyrich, Hoffmann, Pikuz, Faenov, Magunov, Skobelev, Borisenko, Shevelko, Golubev, Fertman, Turtikov and Sharkov2002, Reference Rosmej, Pikuz, Wieser, Blazevic, Brambrink, Roth, Efremov, Faenov, Pikuz, Skobelev and Hoffmann2003, Reference Rosmej, Pikuz, Korostiy, Blazevic, Brambrink, Fertman, Mutin, Shevelko, Efremov, Pikuz, Faenov, Loboda, Golubev and Hoffmann2005b). This method allows determining the projectile ion charge and velocity as a function of the ion penetration depth in the stopping medium. The high spectral (λ/Δλ = 2000–5000) and spatial (30–70 µm) resolutions were achieved using a spherically bend crystal spectrometer and Kodak X-ray films (Faenov et al., Reference Faenov, Pikuz, Erko, Bryunetkin, Dyakin, Ivanenkov, Mingaleev, Pikuz, Romanova and Shelkovenko1994; Rosmej et al., Reference Rosmej, Wieser, Geissel, Rosmej, Blazevic, Jacoby, Dewald, Roth, Brambrink, Weyrich, Hoffmann, Pikuz, Faenov, Magunov, Skobelev, Borisenko, Shevelko, Golubev, Fertman, Turtikov and Sharkov2002).
The spectroscopic method is based on measurements of the characteristic K-shell emission of projectile ions excited in close collisions with target atoms (Kauffman et al., Reference Kauffman, Jamison, Gray and Richard1976). At close-to-zero impact parameters, the probability of the K-shell electron ionization and production of the projectile K-shell vacancy is rather high and depends only slightly on the ion charge state (Rosmej et al., Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a). The resulting autoionizing states are very unstable and can decay via two noncollisional processes—Auger ionization or resonant radiative decay of one of the bound electrons into the K-shell vacancy. In the case of middle Z elements, the time scale of both processes is some tens of femtoseconds (Safronova & Lisina, Reference Safronova and Lisina1979), therefore, de-excitation occurs after the projectile has passed about 500 nm of the stopping medium. Since this is beyond the spatial resolution provided in the experiments, one can suggest that processes of the ion excitation (ionization) in collisions with target atoms and K α-radiation occur from the same part of interaction region.
The energy of the K-shell radiative transitions in ions with different charges does not vary significantly due to shielding effects produced by projectile bound electrons at higher subshells. For example, the wavelength of the K α-transition in an H-like calcium ion (1s-2p) is 0.301 nm, in a Li-like Ca (1s 22s-1s2s2p) is 0.318 nm, and in an F-like (1s 22s 22p 3-1s2s 22p 4) is 0.336 nm. This feature allows us, from one side, to register the K-shell radiation of all projectile charge states by the same X-ray spectrometer, and from the other side, to demand spectral resolution of the detector higher then λ/δλ = 1000. The line intensity distribution of the K-shell transitions arising from ions with different ion charges represents the charge state distribution. The redistribution of the intensities of the K-shell satellites, arising from different ion charge states with the penetration depth in the target, demonstrates the ion charge state evolution along the ion beam stopping path.
The spectroscopic method discussed above was used in experiments on the penetration of a 48Ca10+ ion beam with initial energies of 5.9 MeV/u and 11.4 MeV/u into solid, foam, and gaseous targets. Experiments on the interaction of heavy ion beams with different types of targets were carried out at the Universal Linear Accelerator (UNILAC) of the Gesellschaft für Schwerionenforschung (GSI, Darmstadt). The detailed experimental setup is described by Rosmej et al. (Reference Rosmej, Wieser, Geissel, Rosmej, Blazevic, Jacoby, Dewald, Roth, Brambrink, Weyrich, Hoffmann, Pikuz, Faenov, Magunov, Skobelev, Borisenko, Shevelko, Golubev, Fertman, Turtikov and Sharkov2002, Reference Rosmej, Pikuz, Wieser, Blazevic, Brambrink, Roth, Efremov, Faenov, Pikuz, Skobelev and Hoffmann2003, Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a).
2.2. K-shell Spectra of Calcium Ions Penetrating SiO2 Low-Density Aerogel
In experiments mentioned above, the dependence of the projectile ion K-shell spectra on the penetration depth in the stopping material was measured. Figure 1 show a typical experimental spectrum of Ca projectiles, which have been slowed down in a porous SiO2 target of 0.023 g/cm3 mean density.

Fig. 1. K-shell spectrum of Ca ions with an initial energy of 10.7 MeV/u slowed down in 0.023 g/cm3 SiO2 aerogel. Densitograms demonstrate the evolution of the Kα-satellite spectra with a penetration depth. The ion energy corresponding to the penetration depth is defined from the Doppler line shift.
The use of porous stopping media with a volume density up to 100 times lower than of amorphous quartz (ρ = 2.3 g/cm3) allowed stretching the ion stopping path and resolving the evolution of the K-shell projectile ion and target radiation along the ion trajectory (Rosmej et al., Reference Rosmej, Wieser, Geissel, Rosmej, Blazevic, Jacoby, Dewald, Roth, Brambrink, Weyrich, Hoffmann, Pikuz, Faenov, Magunov, Skobelev, Borisenko, Shevelko, Golubev, Fertman, Turtikov and Sharkov2002, Reference Rosmej, Pikuz, Wieser, Blazevic, Brambrink, Roth, Efremov, Faenov, Pikuz, Skobelev and Hoffmann2003, Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a).
If the high energy monocharged ion beam passes through a solid target, it is ionized in collisions with target atoms. The charge state distribution corresponding to the current projectile velocity will be established at the first hundreds of nanometers in the target. In the spectrum, one can observe intensive K-shell radiation of highly charged H- (1s-2p) and He-like (1s 2-1s2p) calcium ions at the beginning of the ion stopping path (Fig. 1a). Penetrating into the target and loosing the energy ions start to capture bound target electrons. The spectrum at the end of the observed ion stopping path displays the K-shell transitions toward lower charged ions such as Li- (1s 22l-1s2l2l) and Be-like (1s 22l2l-1s2l2l2l) (Fig. 1b). Therefore, K-shell spectra spatially resolved along the ion path in the target “visualize” the evolution of the ion charge state during the ion stopping process.
Another interesting feature of the spatially resolved projectile spectra is a tilted form of the spectra lines. Radiation of ions moving with 1/10 of the speed of light exhibits a relativistic Doppler shift. The value of the shifted wavelength is proportional to the ion velocity. During the penetration in a stopping medium, the ion velocity and therefore the Doppler shift are decreasing continuously imaging the deceleration process. A high spectral resolution (λ/dλ = 3000) of the spherically bend mica spectrometer (Faenov et al., Reference Faenov, Pikuz, Erko, Bryunetkin, Dyakin, Ivanenkov, Mingaleev, Pikuz, Romanova and Shelkovenko1994) allows obtaining the ion velocity dependence with the penetration depth using the Doppler line shift with accuracy of 7%. The method was proved using time-of-flight measurements (Rosmej et al., Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a).
In order to prove the validity of the applied spectroscopic method for the investigation of the ion charge state evolution, the measurements were complemented by the analysis of the charge state distribution of Ca ions emerging from the target. Figure 2a depicts the charge state distribution of Ca ions with a final energy of 6.5 MeV/u after emerging from 8.39 mm thick piece of 0.023 g/cm3 SiO2 aerogel target. The results are obtained using a 1.63T magnet spectrometer. The ion beam energy behind the target measured by means of the time-of-flight method was of 6.5 MeV/u (Rosmej et al., Reference Rosmej, Blazevic, Korostiy, Bock, Hoffmann, Pikuz, Efremov, Fortov, Fertman, Mutin, Pikuz and Faenov2005a; Fertman et al., Reference Fertman, Mutin, Turtikov, Blazevic, Efremov, Golubev, Hoffmann, Korostiy, Pikuz, Rosmej and Sharkov2006).

Fig. 2. (Color online) Experiments on the interaction of 11.4 MeV/u Ca ions with a 8.39 mm thick piece of 0.023 g/cm3 SiO2 aerogel. (a) The charge state distribution of Ca ions measured after the target by means of a magnetic spectrometer. (b) Ca-Kα-radiation observed inside the stopping medium using the X-ray spectroscopy.
Simultaneously, the spatially resolved K-shell spectra were registered. The radiation was observed at 90 degrees with respect to the ion beam axis. Figure 2b shows the characteristic lines occurring due to radiative transitions from one and double excited states 2p, 1s2p, 1s2p2p in Ca 19+–Ca 17+ ions before the projectiles left the target.
The results of these two methods cannot be compared directly since the method of X-ray spectroscopy provides the measurement of the population only of excited ion states with a K-shell vacancy inside the stopping medium. A magnet spectrometer however measures the distribution of the ions over the ground states outside the interaction region.
Numerical simulations have been performed in order to conclude about the charge state distribution of ions inside the target material using the experimental results of the K-shell spectroscopy.
3. POPULATION KINETICS OF THE PROJECTILE GROUND AND EXCITED STATES
A quantitative analysis of the projectile ion population kinetics governed by ion–target atom collisions and noncollisional processes has been performed in order to predict the charge state distributions of fast heavy ions inside stopping matter.
The fraction of projectiles having the charge Z is defined as a sum over the population density of the ion ground and excited states. With growing target density, the population of excited ions starts to be comparable with those in the ground state. The last one influences the total ionization and electron capture cross-sections and leads to the observed dependence of the projectile ion charge state distribution on the target density.
Line intensities of the characteristic projectile spectra measured in the experiments are directly proportional to the populations of excited states with K-shell vacancies giving rise to the corresponding radiative transitions. Therefore, the population of the ion excited states can be measured directly.
The intensity of a spectral line corresponding to the transition from the upper energy level k to the lower i of an atom is given by (Sobelman & Vainshtein, Reference Sobelman and Vainshtein2006):
where A ki is the radiative probability for the transition k → i, P(k) is the population density of ions excited to the level k, ωki is the frequency of the transition, and ħ is Planck's constant divided by 2π. The population of the ion ground states cannot be directly measured inside the stopping medium using projectile self radiation. Hence, it will be then predicted by means of the numerical procedure taking into account all elementary collisional and noncollisional processes connecting the ground and excited states and their dependence on the ion energy, ion charge and density of the stopping matter.
3.1. Collisional and Noncollisional Processes In Projectile Ion–Target Atom Interactions
In order to estimate the distribution of ions over their energy levels due to collisions with target atoms, the following elementary atomic processes have to be taken into account: electron capture and loss (charge exchange), collisional excitation and de-excitation as well as radiative, and Auger decays.
Bound electron capture cross-sections were calculated using the CAPTURE code described in the papers by Shevelko et al. (Reference Shevelko, Tolstikhina and Stöhlker2001) and Shevelko et al. (Reference Shevelko, Rosmej, Tawara and Toltikhina2004). In this code cross-sections of one-electron charge exchange are calculated using the method of multichannel normalization of the capture probabilities in the impact parameter representation. This method employs the relationship between the quasi-classical and the quantum-mechanical charge exchange amplitudes (Shevelko, Reference Shevelko1980). Results of these calculations are presented in Figure 3.
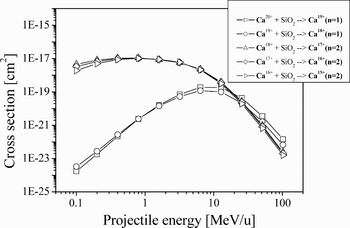
Fig. 3. Dependence of the bound electron captures cross sections for CaZ+ ion ground state in collisions with SiO2 molecules on the ion energy. The calculations were performed using the CAPTURE code.
The LOSS code (Shevelko et al., Reference Shevelko, Tolstikhina and Stöhlker2001) was used to calculate one-electron ionization cross-sections of fast ions colliding with neutral atoms in the momentum transfer representation in the first Born approximation with account of the atomic structure of the target. Calculated by the LOSS code K-shell ionization cross-sections of CaZ+ ions colliding with SiO2 molecules are presented in Figure 4. The computer code also allows estimating the excitation cross-sections of projectiles by the target atoms and molecules. Cross-sections of the de-excitation process were calculated using the principle of detailed balance (the Klein-Rosseland relation) (Klein & Rosseland, Reference Klein and Rosseland1921). In calculations of the charge-changing cross-sections for projectiles colliding with molecule targets, the Bragg's additivity rule was used.
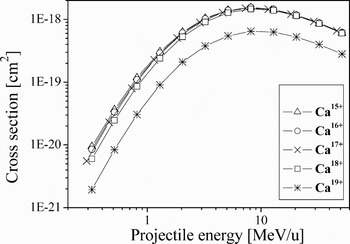
Fig. 4. K-shell ionization cross sections of Ca Z+ ions colliding with SiO 2 molecules as a function of the projectile energy calculated using the LOSS code.
The radiative transition probabilities were calculated using the classical approximation (Lebedev & Beigman, Reference Lebedev and Beigman1998)
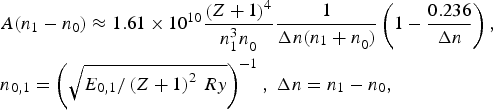
where E 0,1 is the ion energy levels counted from the ionization limit, Z is the ion charge, n 1 and n 0 are the principle quantum numbers of the upper 1 and lower 0 levels, respectively.
3.2. Five State-Collisional-Radiative Model
Numerical calculations of population density of Ca ions colliding with SiO2 target atoms have been performed using the energy level system presented in Figure 5. The chosen model was limited to Ca20+–Ca15+ ions since the observed K-shell spectra in the experiments correspond to the ion charges of Z = 16–19. For every ion charge state, the ground and three excited states without spin-orbital splitting were considered. Autoionizing (double excited) states were neglected in the considered energy level system, since at high projectile velocities they are weekly populated and made no influence on the ion charge fraction in comparison to the ground and nearby states.
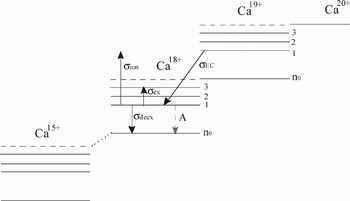
Fig. 5. Schematic drawing of the atomic population kinetics model.
We assume that the distribution inside the same principal quantum number n follows the statistical law that is the case at high densities of the stopping material. The distribution of the population fractions over the ion energy levels is described by a system of the rate equations of the multilevel kinetics. The differential equation for the fraction P of the energy level k of the ion Z can be written as

where P Z′(i) is the population fraction of the level i of the ion charge Z′; B ik are rate coefficients of the atomic processes occurring between the level k of the ion Z and the level i of the ion Z′; B kk denotes the sum of the atomic processes, which depopulate the energy level k of the ion Z. The time is coupled to the coordinates by the projectile velocity.
In atomic physics, the rate of collisional process is given as
where N T is the target density in at/cm3, υ is the projectile velocity, and σcoll is the cross-section of the collisional process in cm2. The quantity R coll characterizes the number of interactions per time unit and has the dimension of s−1. The rate coefficient of the noncollisional processes is introduced by the radiative decay rate A in s−1.
Since the rates of collisional processes are directly proportional to the target density, and radiative decay rates are characterized only by the ion energy level structure, the dependence of the ion population over excited states on the target density takes place.
The population fraction P Z(k) is defined from equilibrium state dP Z(k)/dt = 0:
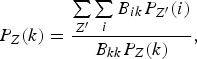
The system of 21 linear equations in regard to P Z(k) has been solved. The set of differential equations was considered in the form of a matrix equation BP = a. B is the matrix of collisional and noncollisional rate coefficients, which connects the ground and excited states of ions and is written by

The column vector P denotes populations of the energy states:

Since dP Z(k)/dt = 0, the vector is equal 0. At − B kk = ∑i≠kB ik the matrix system is singular. Therefore, one of the equations was replaced by the conservation law of the number of particles, ∑Z,kP Z(k) = 1. The system of linear equations
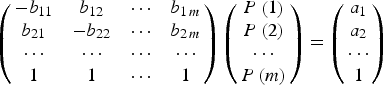
was solved with respect to P(m) using the Gaussian elimination method.
3.3. Comparison with experiments
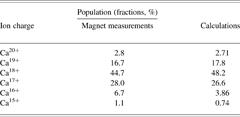
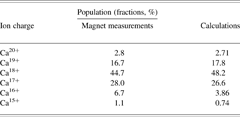
The validity of the numerical calculations of the population kinetics has been compared with measurements. The charge state distribution of Ca ions after emerging from 8.39 mm thick peace of 0.023 g/cm3 silica aerogel performed by means of a magnetic spectrometer was compared with calculations at the same ion energy of 6.5 MeV/u. The results are shown in Figure 6. In order to notice the difference between measurements and calculations, the numbers are presented in Table 1. The fraction of projectile ions with a charge Z was defined as the sum over the population density of the ion ground and excited states.

Fig. 6. Calcium ion charge state distribution measured by a magnetic spectrometer after the aerogel target and calculated using the collisional-radiative model at the projectile energy of 6.5 MeV/u.
Table 1. The population fractions of calcium ions obtained by the magnet measurements and numerical calculations
Measurements of the ion charge states after the stopping medium were accomplished by a spatially resolved spectroscopic analysis of the projectile radiation (Fig. 2b). The calculated relative intensities of Lyα (Ca19+) and Heα (Ca18+) characteristic lines at the ion energy of 6.5 MeV/u before the ion beam left the target coincide very well with experimental ratio (Table 2).
Table 2. Measured and calculated data of relative line intensities for the experiment on the interaction of Ca ions with a 8.39 mm thick piece of 0.023 g/cm3 SiO2 aerogel (Fig. 2b)
In conclusion, we would like to note that the numerical calculations are in close agreement with experimental measurements of the charge state distribution of calcium ions inside and behind a stopping medium. The described collisional-radiative model is capable to predict the ion charge evolution during the energy loss process under different stopping conditions. Using the measured dependence of the projectile velocity on the ion penetration depth for the calculation of rate coefficients of collisional processes it is now possible to analyze the behavior of the projectile K-shell radiation along the ion stopping path in the target material.
3.4. Dependence of the Calcium Ion Subshell Structure on the Target Density. Results and Discussion
The influence of the target density on the population of the projectile ion subshells is governed by the competition between collisional and noncollisional processes responsible for the depopulation of excited bound electrons. For a better understanding of this problem, let us introduce the quenching factor β(n), which is defined as the ratio of the collisional and radiative rates for the depopulation of the ion excited state with a principal quantum number n:
where υ is the ion velocity, σcoll is the collisional depopulation cross section, N T is the target density, and A is the radiative decay rate. Collisional depopulation can occur via de-excitation to lower energy levels and due to further excitation or ionization into continuum. Let us consider the dependence of the quenching factor on the most important projectile ion and target parameters.
The corresponding ionization and radiative rate coefficients can be scaled as
where Z is the ion charge and n is the principal quantum number of the ion excited state.
Therefore, for the quenching factor one obtains the following dependence:
As follows from Eq. 12, the factor β(n) grows strongly with the increase of the principal quantum number n of the excited bound electron and with the target density, and decreases with the projectile velocity and the ion charge.
In Figure 7 we have plotted quenching factors for H-like 6 MeV/u Ca ions colliding with SiO2 of different target densities. In the calculations, collisional and radiative processes were taken into account, which depopulate Ca19+ excited energy levels with principal quantum numbers n = 1, 2, 3.
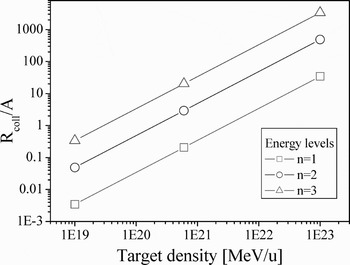
Fig. 7. Quenching factors β(n) calculated for three excited states (n = 1, 2, 3) of 6 MeV/u Ca19+ ions as a function of SiO2 target density.
The quenching factor β = 1 means that 50% of the excited bound electrons decay radiatively to the ground state and 50% are ionized or excited to the higher ion levels.
Figure 7 demonstrates that practically all excited electrons populating n = 1, 2, 3 levels in H-like Ca19+ ions undergo the radiative relaxation to the ground state 1s at the target density of 1019 at/cm3.
At higher target densities, when the quenching factor is larger then 1, the depopulation of the excited states is governed mostly by collisional processes. This leads to the increased population of excited states with respect to the ion ground state as one can see in Figure 8.
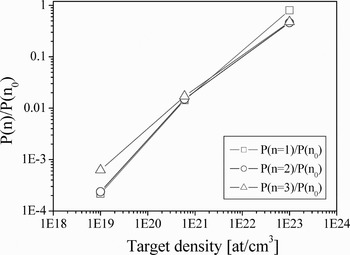
Fig. 8. Population density P(n) of 6 MeV/u Ca19+ ions calculated for three excited (n = 1, 2, 3) states and normalized with respect to the population of the ground state P(n 0).
With growing target densities, the population of the excited ions becomes comparable to the ground one since the time between collisions is short to allow the radiative relaxation to the ground state. Successive collisions of excited ions with target atoms lead to additional and very effective channels of ionization and result in the increase of the total ionization rate:
where P n0 and P n* are the population densities of the ground and excited states, respectively; σion(n) is the ionization cross-section from the level with the principal quantum number n. Due to low binding energies of the excited energy levels, the ionization cross-sections σion(n) can be much higher than those for the ion ground state σion(n 0). At low target densities, P n* is negligible compared to the ground state (Fig. 6), and the ionization is defined by the first term P n0σion(n 0) in Eq. (13). With growing target density, the total ionization cross-section exceeds the total cross section calculated for the low density case by a factor of ten and more (Fig. 9).
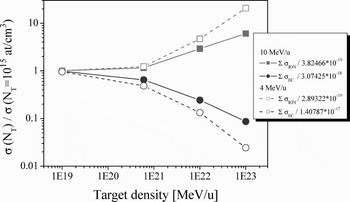
Fig. 9. Calculated total ionization and bound electron capture cross sections of Ca19+ ions interacting with SiO2 atoms as a function of the target density. They are normalized to the cross sections at very low target density 1015 at/cm3, at which the depopulation of the excited levels is governed by radiative processes.
Collisions influence not only the effective ionization cross-sections, but lead as well to the suppression of the bound electron capture to the projectile excited states. At low ion energies, target electrons can be captured with a high probability to the projectile excited state having quenching factors bigger than 1. High rates of collisional depopulation prevent the stabilization of the capture process via relaxation to the ground state: captured target electrons will be immediately ionized (Shevelko et al., Reference Shevelko, Tawara, Ivanov, Miyoshi, Noda, Sato, Subbotin and Tolstikhina2005).
Calculations of the total ionization and recombination cross-sections for H-like Ca ions interacting with SiO2 medium of different densities are presented in Figure 9.
Total ionization cross-sections were calculated according to Eq. (13), while the total captures cross-sections according the following equation:
where σEC(n) is the cross-section of the bound electron capture to the ion level with a principal quantum number n, β(n) is the quenching factor for this level. The populations of the ion ground and excited states as well as quenching factors were calculated using the described collisional–radiative model. From Eq. (14) one can see that only capture to the ion excited levels with low damping factors contributes to the charge change process.
The influence of collisional processes on the total bound electron capture cross-sections is more effective at lower projectile energies since the target electron will be captured to the higher excited level n with a quenching factor growing as n 7. From Figure 9 one can see that at 4 MeV/u ion energy and solid target density, the capture process is 50 times less effective than at the density corresponding to 1 bar gas pressure. For Ca19+ ions of 10 MeV/u it is only a factor of 10.
The increase of the total ionization rates and the suppression of the capture processes at high target densities lead to an increase of the ion charge state inside the stopping medium. Equilibrium charge state distributions of 6 MeV/u Ca ions in a solid quartz of 1023 at/cm3 density and a gaseous target of 1019 at/cm3 density have been calculated by means of the described collisional-radiative model. The results are presented in Figure 10. The Ca ion mean charge in solid matter is of 〈Z〉 = 19.1, while in gaseous one is of 〈Z〉 = 17.34.
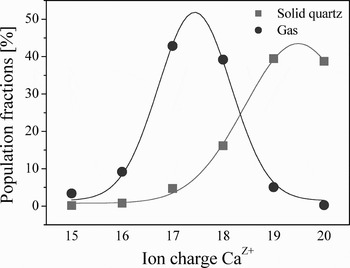
Fig. 10. Equilibrium charge state distributions of 6 MeV/u Ca ions in solid quartz (1023 at/cm3) and gaseous medium (1019 at/cm3) calculated using the five-state model.
The calculated equilibrium mean charge in solid SiO2 is in good agreement with measurements of Shima (Shima et al., Reference Shima, Ishihara and Mikumo1982) giving 〈Z〉 = 18.57 for 6 MeV/u Ca ions penetrating a carbon foil. The difference can be explained by the dependence of collisional cross sections on the target atomic number.
4. CONCLUSION
A quantitative analysis of the ion subshells population kinetics in the projectile–target interaction process has been performed. A five charge-state collisional-radiative model has been created, which considers the ground and three excited states for each ion charge. Numerical calculations account for collisional and noncollisional processes of the ion population kinetics for 21 ground and excited states, and allowed the prediction of the projectile charge state distribution inside stopping medium.
The model was satisfied compared with the ion charge state distribution measured after the SiO2 foam target by means of a magnet spectrometer. The calculations have shown a good agreement with the measured projectile K-shell spectra.
The gas-solid difference of the ion charge state distribution has been numerically demonstrated. The calculations have shown that the increase of the ion charge in a solid target can be explained by the increase of the total ionization rate, and the suppression of the bound electron capture process. The suppression of the bound electron capture starts to be dominant at the ion velocity providing the capture to the ion excited states with large damping factors β.
Summarizing we would like to stress out, that the selection of proper experimental conditions for a demonstration of the gas-solid effect requires a detailed knowledge of the rates of elementary processes governing the population of ion electronic subshells.
Acknowledgment
This work has been supported by the project BMBF 06 DA 116.