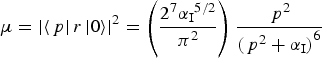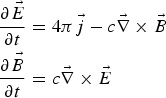1. INTRODUCTION
The ionization process of atoms and the plasma evolution by implementing a high intensity optical field (an ultra-short laser pulse) are of general interest in plasma physics, because of the different applications including inertial confinement fusion, laser-plasma accelerator, and X-ray lasers. It is turned out that the ionization process by a non-relativistic intense laser pulse (I < 1018 w/cm2) can significantly influence the laser–plasma interaction. In this way, pre-pulse effects due to ionization can strongly influence the main pulse propagation (Hosokai et al., Reference Hosokai, Kinoshita, Ohkubo, Maekawa, Uesaka, Zhidkov, Yamazaki, Tomassini, Giulietti and Giulietti2006). The ionization effects have extensively been investigated theoretically and experimentally to realize the important phenomena such as above threshold ionization (Becker et al., Reference Becker, Grason, Kopold, Milosevic, Paulus and Walther2002; Frolov et al., Reference Frolov, Knyazeva, Manakov, Geng, Peng and Starace2014), laser frequency blue shifting (Chessa et al., Reference Chessa, De Wispelaere, Dorchies, Malka, Marques, Hamoniaux, Mora and Amiranoff1999), ionization induced diffraction (Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010), self-defocusing (Efimenko & Kim, Reference Efimenko and Kim2011), and ring formation (Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997).
The detailed study of ionization processes is rather complicated even by exploiting the recent methods of radiation and particle beam generation (Liu et al., Reference Liu, Xia, Wang, Lu, Wang, Deng, Li, Zhang, Liang, Leng, Lu, Wang, Wang, Nakajima, Li and Xu2011; Wang et al., Reference Wang, Li, Sheng, Lu and Zhang2013). The field-ionized plasma differs completely from the commonly known plasma in the sense of electron–ion correlation. In the case of the field-ionized plasma, the electron and ion are strongly correlated. In this case, the electron can frequently reach the parent ion vicinity during the field interaction. It is worth mentioning that except for trapped particles, the electron trajectory is always enclosed in the plasma. When the electron returns to the original ion, interesting radiation phenomena like dipole radiation become possible. In this way, the strong nonlinear effects such as the generation of highly energetic photons (high harmonic generation, HHG) happen. HHG is firstly explained by semi-classical (Corkum, Reference Corkum1993; Schafer et al., Reference Schafer, Yang, DiMauro and Kulanderc1993) and quantum mechanical (Lewenstein et al., Reference Lewenstein, Balcou, Ivanov, L'Huillier and Corkum1994) three-step model, which is designed according to the response of a single atom in relatively weak electromagnetic fields (for example 1013~1014 w/cm2, for a hydrogen atom). Based on this model, the electronic wave function of an atom is partially freed by a strong laser field [the wave function of the electron can be expressed as 
${\rm \psi} ({r},{t}) = {{\rm \alpha} _0}{{\rm \psi} _0}({r},{t}) + {{\rm \alpha} _{\rm p}}{{\rm \psi} _{\rm p}}({r},{t})$, where 
${{\rm \psi} _0}({r},{t})$ is the ground state and 
${{\rm \psi} _{\rm p}}({r},{t})$ is a continuum state with the momentum p. α0 and αp represent the population of these states]. The ionized electron is accelerated in the local fields and finally the ionized and bound-state portions of the electronic wave packet interfere with each other giving rise to a strong dipole response that leads to the emission of highly energetic photon along with the recombination of the electron with the bound state. The maximum energy, cut-off energy, that can be generated within this model is I p + 3.17 U p, where I p and U p are the binding energy of the electron in the atom and the ponderomotive energy in the laser field, respectively. The detailed study of HHG in this regime was one of the most often studied aspects of intense laser physics during the past decades (Mocek et al., Reference Mocek, Sebban, Bettaibi, Zeitoun, Faivre, Cros, Maynard, Butler, Mckenna, Spence, Gonsavles, Hooker, Vorontsov, Hallou, Fajardo, Kazamias, Lepape, Mercere, Morlens, Valentin and Balcou2005; Strelkov, Reference Strelkov2006; Ciappina et al., Reference Ciappina, Chirilă and Lein2007; Ozaki et al., Reference Ozaki, Elouga Bom, Ganeev, Kieffer, Suzuki and Kuroda2007; Colosimo et al., Reference Colosimo, Doumy, Blaga, Wheeler, Hauri, Catoire, Tate, Chirla, Maech, Paulus, Muller, Agostin and Dimauro2008; Shiner et al., Reference Shiner, Trallero-Herrero, Kajumba, Bandulet, Comtois, Legare, Giguere, Kieffer, Corkum and Villeneuve2009; Falcao-Filho et al., Reference Falcao-Filho, Gkortsas, Gordon and Kartner2009; Ghimire et al., Reference Ghimire, Dichiara, Sistrunk, Agostini, Dimauro and Reis2010; Gkortsas et al., Reference Gkortsas, Bhardwaj, L Falcão-Filho, Hong, Gordon and X Kärtner2011; Klaiber et al., Reference Klaiber, Kohler, Hatsagortsyan and Keitel2012; Bleda et al., Reference Bleda, Yavuz, Altun and Topcu2013).
However, ionization occurs immediately after the laser intensity is increased to a higher level (this happens in many practical cases). In this case, the electron wave function in the majority of its closed trajectory is completely free (α0 = 0) and it can approach to the ground state wave function only through the spontaneous emission process (radiative recombination) (Kohler et al., Reference Kohler, Ott, Raith, Heck, Schlegel, Keitel and Pfeifer2010). It should be noted that the amount of this laser intensity depends on the type of atom (e.g., this intensity for hydrogen atom is I > 1015 w/cm2). The purpose of this paper is to investigate the plasma radiation that is produced in this regime. In this way, a heuristic algorithm based on particle-in-cell (PIC) code is introduced for the simulation of radiative recombination during the ionization and formation of plasma when a laser pulse with intensity 1016~1017 w/cm2 is passed through hydrogen atoms.
PIC is one of the most successful numerical methods, which is exploited to study the laser–plasma interactions (Birdsall et al., Reference Birdsall, Langdon, Vehedi and Verboncoeur1991; Hockney & Eastwood, Reference Hockney and Eastwood1998; Yazdanpanah & Anvary, Reference Yazdanpanah and Anvary2012). The general distribution functions are statistically derived in phase space by solving the Maxwell equations and Lorentz equations of motion, simultaneously. The PIC method employs the fundamental equations with a minimum number of approximations so as to preserve the physical notions. Therefore, unlike the single particle model, the space charge and other collective effects in the field-ionized plasma are taken into account in our PIC model. Therefore, the results of the PIC simulation can be more precise than the numerical calculation using the single particle model. The ionization phenomena have already been studied by considering the field ionization calculation in PIC method in the absence of radiative recombination (Janulewicz et al., Reference Janulewicz, Grout and Pert1996; Bruhwiler et al., Reference Bruhwiler, Dimitrov, Cary, Esarey, Leemans and Giacone2003; Kemp et al., Reference Kemp, Pfund and Meyer-ter-Vehn2004; Chen et al., Reference Chen, Cormier-Michel, Geddes, Bruhwiler, Yu, Esarey, Schroeder and Leemans2013). In our paper, two Monte Carlo packages are simultaneously added to the usual one-dimensional (1D)-2 V PIC (Yazdanpanah & Anvary, Reference Yazdanpanah and Anvary2012) for considering the ionization and the radiative recombination to measure the harmonics that are generated during the ionization of hydrogen atoms. The ionization process is modified according to the following considerations:
• The theoretical and numerical expressions (Landau & Lifshitz, Reference Landau and Lifshitz1965; Mur & Popov, Reference Mur and Popov1993; Bauer & Mulser, Reference Bauer and Mulser1999) for the ionization rate are considered according to the value of the electric field strength.
• In the presence of the laser electric field, the Stark shift of the ground state of hydrogen atom is implemented according to Eq. (7) (Mur & Popov, Reference Mur and Popov1993).
• Despite the previous works, nonzero initial momentum is envisaged for the ejected electrons (Delone & Krainov, Reference Delone and Krainov1991; Krainov & Shokri, Reference Krainov and Shokri1995).
The energy gain produced by recombination is considered to satisfy energy conservation by introducing an artificial recombination current, in consistence with the case of ionization. By the use of this artificial current, Maxwell's equations are solved in the separate mesh to calculate the generated fields by harmonic emissions. The simulation results are presented for the responses of the formed plasma and the harmonic generated fields.
It should be noted that the harmonics investigated in this work differ from the harmonic generation in laser–solid interactions due to the nonlinear relativistic oscillation of the plasma components (Shuai et al., Reference Shuai, Shen, Li and Xu2002; Dromey et al., Reference Dromey, Bellei, Carroll, Clarke, Green, Kar, Kneip, Markey, Nagel, Willingale, Mckenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2009; Shoucri & Afeyan, Reference Shoucri and Afeyan2010; Dollar et al., Reference Dollar, Cummings, Chvykov, Willingale, Vargas, Yanovsky, Zulick, Maksimchuk, Thomas and Krushelnick2013). This area is completely classical in nature and differs from our case, which is based on quantum mechanics.
The paper is organized as follows: Section 2 contains a general presentation of the physical description of the model. In Section 3, we describe our numerical PIC code and study ionization and recombination processes step by step. We then illustrate the simulation results in Section 4. The summary is given in Section 5.
2. PHYSICAL DESCRIPTION
When an atom is exposed to an ultrahigh optical intensity, electrons can be liberated from the atom through different mechanisms. Keldysh (Reference Keldysh1964) introduced the parameter γ as
$${\rm \gamma} = \displaystyle{{{{\rm \omega} _{\rm L}}\sqrt {2{{I}_{\rm p}}}} \over E},$$
and demonstrated that the values γ ≪ 1 and γ ≫ 1 are corresponding to the Tunneling Ionization (TI) and multiphoton ionization, respectively. In Eq. (1), I p, ωL, and E are the respective atomic ionization potential, the frequency and amplitude of laser electric field (atomic units will be used throughout this section). In the case γ ≪ 1, when the atom is in an external field, the Coulomb potential barrier is lowered and the electron can tunnel through this barrier. When the laser electric field is strong enough, such that E > E critical [Bauer has shown that this critical value for atomic hydrogen is given by E critical = 0.146a.u. (Bauer, Reference Bauer1997)], the electron is able to escape (not to tunnel) over the barrier formed by the Coulomb potential and the laser field. This ionization mechanism is called Barrier Suppression Ionization (BSI). The released electron by field ionization is localized around the nucleus at the distance R 0. R 0 is comparable with the Bohr radius (the size of the Bohr radius is 
${{a}_0} = \hbar /{{m}_{\rm e}}{c}{\rm \alpha} $ that 
$\hbar $, m e, c, and α are reduced Planck's constant, the electron rest mass, the speed of light in vacuum, and the fine structure constant, respectively).
One of the most studied nonlinear phenomena that can occur during the ionization of atoms is HHG, in which the system emits radiation at multiples of the laser frequency. In this paper, we want to introduce a new numerical model based on PIC simulation to investigate the harmonic generation during the ionization. In this way, the following expressions can elaborate the model configuration:
(1) We consider high intensities in γ ≪ 1 (laser pulse with peak intensity
${10^{16}} \sim {10^{17}}\,{\rm w}{/}{\rm c}{{\rm m}^2}$ and wavelength λL = 1 μm). In this case, the hydrogen atoms are immediately ionized. Based on strong-field approximation (Keldysh, Reference Keldysh1964; Faisal, Reference Faisal1973; Reiss, Reference Reiss1980) the electron wave function becomes completely free. Therefore, the wave function in the continuum state can be described by a plan wave (| p〉).(2) The electron in the continuum state treats as a free particle moving in the local electric field with no effect of atomic potential. Furthermore, the intensities are large enough (1016 ~ 1017 w/cm2) to ignore the continuum–continuum transitions (Lewenstein et al., Reference Lewenstein, Balcou, Ivanov, L'Huillier and Corkum1994) (The continuum–continuum transitions occur when the velocity of the ionized electron is low. Here, due to the high laser intensity, these transitions can be ignored).
(3) The electron in continuum state could transit to the ground state of hydrogen atom (| 0〉) and produce harmonic generation through radiative recombination. The transition amplitude is given by the following equation in the length gauge (Lewenstein et al., Reference Lewenstein, Balcou, Ivanov, L'Huillier and Corkum1994),
(2)where$${\rm \mu} = {\left \vert {\left\langle {\,p} \right \vert {r}\left \vert 0 \right\rangle} \right \vert ^2} = \left( {\displaystyle{{{2^7}{{\rm \alpha} _{\rm I}}^{5/2}} \over {{{\rm \pi} ^2}}}} \right)\displaystyle{{{{\,p}^2}} \over {{{({{\,p}^2} + {{\rm \alpha} _{\rm I}})}^6}}}$$${{\rm \alpha} _{\rm I}} = 2{{I}_{\rm p}} = 1$. We consider the recombination of an electron with its nearest Hydrogen ion. According to the quasi-classical three-step model, the electrons are only able to return to the parent ions, depending on the phase of the electric field at the instant of ionization. In this model, most electrons are produced at unfavorable phases of the electric field and never return to the core. Although this process properly explains various features of HHG, it does not mean that the other atoms play no role. However, an electron freed through ionization may recombine either with its parent ion or with other ions in its vicinity. For example, consider x = R to be the distance between a parent ion with respect to that of recombined with an electron in a linear-polarized electric field ${\rm (}{E} = {{E}_0}\cos ({{\rm \omega} _{\rm L}}{t}){\rm )}$. By solving the equation of motion in the non-relativistic intensity for the electron position under the initial conditions $x{(}{t_{\rm i}}{) = 0}$ and ${\dot x}({{t}_{\rm i}}) = 0$, we obtain the following relation:
(3)in which t i is the ionization time, and t r the time of the recombination of the electron emitted during the ionization with the nearest neighbor ion. In dependence on the distance R, these times are rather different.$${R} = \displaystyle{E \over {{{\rm \omega} _{\rm L}}^2}} \left[ {(\cos ({{\rm \omega} _{\rm L}}{{t}_{\rm r}}) - \cos ({{\rm \omega} _{\rm L}}{{t}_{\rm i}}) + {{\rm \omega} _{\rm L}}({{t}_{\rm r}} - {{t}_{\rm i}})\sin ({{\rm \omega} _{\rm L}}{{t}_{\rm i}})} \right],$$
3. ONE DIMENSION PIC SIMULATION
In this paper, the simulation box is extended by 170 µm in x direction (1D geometry). A uniform neutral Hydrogen gas that is initially distributed within the region of 60–120 µm, was used as the plasma source. A laser pulse of Gaussian profile enters with a linear polarization in the y direction from the left side of simulation box and passes through the hydrogen atoms, as illustrated in Figure 2. The laser pulse wavelength is λL = λ0 = 1 μm and the number density of the initial neutral hydrogen atoms is 0.007 n cr, where 
${{n}_{\rm cr}} = {\rm \pi} {{m}_{\rm e}}{{c}^2}/{e^2}{{\rm \lambda} _{\rm L}}^2 $ represents the critical density. In this simulation, we use 20 macro-particles/cell that are initially distributed within the region of 60–120 λL, uniformly. The grid spacing is δx = 0.005 µm throughout simulations. As mentioned in the previous section, the electron radiation is considered as a three-step process: Ionization, acceleration in a local field, and radiative recombination with the nearest center. Our PIC algorithm process is developed according to these three steps. In this way, two Monte Carlo packages are added to the usual relativistic and fully electromagnetic 1D-2 V PIC code algorithm (Yazdanpanah & Anvary, Reference Yazdanpanah and Anvary2012) to consider the ionization and the recombination steps. In the following, we explain the three steps in detail.
3.1. Fundamental Equations of Usual Electromagnetic 1D-2 V PIC Code
In the PIC method, the gas is represented by a number of macro-particles that move in a domain described by a computational mesh. All the volume of particles is divided by a set of mesh cells and every point of the considered space belongs to one of the existing cells of a mesh. The fixed and time independent set of cells is usually used for this task. A number of finite particles present the continuous medium of plasma or beam. Each finite particle has a mass, charge state, and coordinates in the phase space of motion. In order to describe atomic processes and to effectively calculate Coulomb interactions among the charged particles, the best way is to have densities of each type of physical particle in the mesh. A sufficient number of finite particles of each species should be in each cell for this purpose. The number of real particles corresponding to a super-particle must be chosen such that sufficient statistics can be collected on the particle motion.
The usual PIC algorithm is fully described by one of the authors (Yazdanpanah & Anvary, Reference Yazdanpanah and Anvary2012). In the following, we only explain the basic equations in the PIC simulation. For many types of problems, the PIC method is relatively intuitive and straightforward to implement. A diagrammatic representation of one time step of the simulation is illustrated in Figure 1. As shown in this figure, the method typically includes the following procedures:
• Integration of the (Newton–Lorentz) motion equations:
(4)In Eq. (4),$$\displaystyle{{{d}\vec v} \over {{dt}}} = \displaystyle{{q} \over {m}}({\vec E} + \displaystyle{{\vec v} \over {c}} \times \vec B)$$$\vec v$, $\vec E$ and $\vec B$ are the charged particle velocity, the electric and magnetic field in plasma and m and q are the particle mass and charge, respectively.• Interpolation of charge and current source terms to the field mesh.
• Computation of the fields on mesh points using the following Maxwell equations:
(5)$$\eqalign{& \displaystyle{{\partial \vec E} \over {\partial {t}}} = 4{\rm \pi} \vec j - c\vec \nabla \times \vec B \cr & \displaystyle{{\partial \vec B} \over {\partial {t}}} = {c}\vec \nabla \times \vec E} $$$\vec j$ is the current.• Interpolation of the fields from the mesh to the particle locations.
In our code, reflecting and open boundary conditions have been applied to the particles and fields, respectively. The results of this code can be accurate, as long as the formed plasma is non-collisional. The 1D geometry is applicable here for the laser spot size larger than the laser wavelength and for the Rayleigh length larger than the laser propagation length.
Fig. 1. A diagrammatic representation of one time step of the PIC simulation. The particles are numbered k = 1, 2, 3,…; the grid indices are i.
3.2. Field Ionization
There are many theoretical reports about the rate of field ionization for hydrogen atoms in the region of TI and BSI. Bauer and Mulser (Reference Bauer and Mulser1999) have compared their results with a numerical solution of the time-dependent Schrodinger equation for an electron involved in the Coulomb potential of a hydrogen atom. They proposed a combined formula (a combination of theoretical and empirical formula) for the ionization rate, which is used in this paper for the region E < 0.175 as
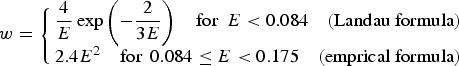$$w = \left\{ {\matrix{ {\displaystyle{4 \over E}\exp \left( { - \displaystyle{2 \over {3E}}} \right)\quad {\rm for } \, \ E \lt 0.084\quad (\hbox{Landau formula})} \cr {2.4{E^2}\quad {\rm for}\,\ 0.084 \le E \lt 0.175\quad (\hbox{emprical formula})} \cr } } \right. $$The numerical calculations of Mur and Popov in a strong electric field demonstrate that the values of the Stark shift associated with the ground state of hydrogen atom are greatly diminished by increasing the field strength, which is in contrast with the second-order perturbation theory (Mur & Popov, Reference Mur and Popov1993). In this case, the determined ionization rates can be correctly fitted by the following equation
$${w} = 1.29\,E - 0.15\quad {\rm for}\, \ 0.175 \le E \le 0.8.$$It should be noted that the boundary values of electric field in Eqs. (6) and (7) are determined by assuming the continuity of ionization rate. When the number of the ionized electrons increases, the space charge effects are also important; consequently they can be taken into consideration. Therefore, the electric field E in the Eqs. (6) and (7) is considered as the superposition of the laser electric and space charge fields [the atomic units are used in Eqs. (6) and (7)]. Likewise, the electric fields due to the space charge effects are entered into the code by using Maxwell Eq. (5).
Contrary to the most simulation codes, we consider here an initial velocity for the particles just after ionization to achieve the most accurate results. The expression for the rate of ionization in the non-relativistic regime for a fixed value of electron momentum p by linearly polarized radiation was obtained in (Delone & Krainov, Reference Delone and Krainov1991; Krainov & Shokri, Reference Krainov and Shokri1995) as:
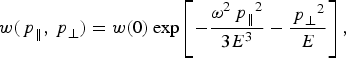$${w}({{\,p}_\parallel}, {{\,p}_ \bot} ) = {w}(0)\exp \left[ { - \displaystyle{{{{\rm \omega} ^2}{{\,p}_\parallel} ^2} \over {3{E^3}}} - \displaystyle{{{{\,p}_ \bot} ^2} \over E}} \right],$$
in which 
${{\,p}_\parallel} $ and 
${{\,p}_ \bot} $ are the respective components of photoelectron momentum along and normal to the axis of laser field polarization. In Eq. (8), the factor 
$\exp \left[ { - {{\rm \omega} ^2}{{\,p}_\parallel} ^2 /3{E^3} - {{\,p}_ \bot} ^2 /E} \right]$ determines the kinetic energy distribution of the ejected electrons. The value of the pre-exponential factor in Eq. (8), w(0), is the same ionization rate as obtained in Eqs. (6) and (7).
The implementation of the ionization process in a PIC code is straightforward. Initially, all electrons are bounded to the atoms. At each time step δt, for each neutral particle, the local electric field and particle ionization parameters [such as ionization potential and the initial momentum that is predicted in the exponential factor of Eq. (8)] are continuously used to calculate the ionization rate w(t). The ionization probability is then given by p i = 1−exp[−w(t)δt], which is usually approximated as p i = w(t)δt in the case of 
${{\,p}_{\rm i}} \ll 1$. The code generates a random number P 0 with a uniform distribution between 0 and 1. If P 0 < P i, the ionization is done and an electron is formed at the location of ion with nonzero velocity. Otherwise, the particle will not be ionized and will be evaluated during the next time step.
According to the energy conservation, the energy loss due to ionization should continuously be considered. This is done by adding an artificial ionization current j ion to the main current in Eq. (5) at each time step. This artificial ionization current 
${\vec j_{\rm ion}}$ is directed along the local electric field 
$\vec E$, and is defined by the following equation (Mulser et al., Reference Mulser, Cornolti and Bauer1998; Kemp et al., Reference Kemp, Pfund and Meyer-ter-Vehn2004; Chen et al., Reference Chen, Cormier-Michel, Geddes, Bruhwiler, Yu, Esarey, Schroeder and Leemans2013)
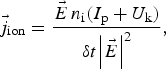$${\vec j_{\rm ion}} = \displaystyle{{\vec E\,{{n}_{\rm i}}({I}_{\rm p}} + {{U}_{\rm k}}) \over {{\rm \delta} {t}{{\left \vert {\vec E} \right \vert} ^2}}},$$in which n i and U k are associated with the number density of the ionized electrons in each time step (which is calculated in the code, routinely) and their initial energies after ionization, respectively.
3.3. Recombination
In our code, the recombination process is carried out by the following steps: The rate of radiative emission in the dipole approximation is given by (Svelto, Reference Svelto1998):
$${{\rm \Gamma} _{\rm rad}} = \displaystyle{{{{\rm \omega} ^3}{{\rm \mu} ^2}} \over {3{\rm \pi} {{\rm \varepsilon} _0}\hbar {{c}^3}}} = \displaystyle{{4{\rm \alpha} {{\rm \omega} ^3}{{\rm \mu} ^2}} \over {3{{c}^3}}},$$
where 
${\rm \omega} = [(1/2)m{v^2} + {{I}_{\rm p}}]/\hbar $ is the emission frequency, ε0 is the vacuum permittivity, 
$\hbar $ is the Planck constant, c is the speed of light, and α is the fine structure constant. In Eq. (10), μ is the transition amplitude that is defined in Eq. (2).
At each time step, the charged particles are sorted by their positions. For each ion, the electrons that are located in distance r ≤ R 0 are listed. With the use of Eq. (10), the radiative emission rate is obtained. Then, by adopting the same procedure in the ionization stage, the recombination probability P r is calculated for the first electron according to the list. The code generates a random number P 0 with a uniform distribution between 0 and 1. If P 0 < P r, the recombination is done and a neutral particle is formed at the location of ion with the ion velocity. Otherwise, the recombination probability is calculated for the second electron listed and a new random number is generated. This process will continue, until all electrons that exist in the distance r ≤ R 0 are dealt with.
The energy conservation law also requires that the energy produced by the recombination of electron with ion is added to the electromagnetic field in each cell. This is done by adding an artificial recombination current j rec to the current in Eq. (5) at each time step throughout the simulation. The same as the ionization stage, it is done by introducing an artificial current j rec as
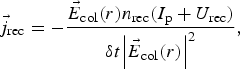$${\vec j_{\rm rec}} = - \displaystyle{{{{\vec E}_{{\rm col}}}({r}){{n}_{{\rm rec}}}({{I}_{\rm p}} + {{U}_{\rm rec}})} \over {{\rm \delta} {t}{{\left \vert {{{\vec E}_{\rm col}}({r})} \right \vert} ^2}}},$$
where n rec and U rec represent the number density of recombined electrons in each time step (which is calculated by using a counter in the code, routinely) and their kinetic energies, respectively, and 
${\vec E_{\rm col}}({r})$ represents the mean Coulomb field that is exerted on the electron by the ion.
In order to calculate the generated fields by harmonic emissions, in our code for the first time, Maxwell's equations are solved in the separate mesh utilizing the artificial current j rec. In fact, choosing the separate mesh is necessary in order to avoid mixing the harmonic fields with numerical noise levels. Meanwhile, the initial values of both the harmonic electric and magnetic fields are assumed zero.
4. SIMULATION RESULTS AND DISCUSSION
The plasma response and harmonic spectrum have been calculated by our PIC code for several cases. Figure 2 illustrates the density and momentum of the liberated electrons along the propagation direction x for the normalized laser intensity 
${{a}_0} = e{E_{\rm L}}/{{m}_{\rm e}}{{\rm \omega} _{\rm L}}{c} = 0.6$ at (a) 
${{t}_1} = 40\,{{\rm \omega} _{\rm L}}^{ - 1} $ and (b) 
${{t}_2} = 160\,{{\rm \omega} _{\rm L}}^{ - 1} $. It is evident that the pulse has enough intensity to ionize the hydrogen atoms, instantly. It is seen that a wake wave is expectably excited by the laser pulse in the field-ionized plasma.
Fig. 2. The PIC simulation results for the laser electric field E y (black curve) normalized by 
${E_0} = {{\rm \omega} _{\rm L}}{m_{\rm e}}{c}/{{q}_{\rm e}}$, the density of the ionized electrons n e (blue curve) normalized by the initial H atoms density n 0, and the momentum of the electrons p x (red curve) normalized by p 0 = m ec for a 0 = 0.6 at (a) 
${{t}_1} = 40{{\rm \omega} _{\rm L}}^{ - 1} $, and (b) 
${{t}_2} = 160{{\rm \omega} _{\rm L}}^{ - 1} $.
The laser electric field E y/E 0 and harmonic emissions field E yh/E 0 are, respectively, demonstrated by the left and right vertical axes against the horizontal axis x/λ0 in Figure 3, for a 0 = 0.6 at the typical times (a) 
${{t}_1} = 40\,{{\rm \omega} _{\rm L}}^{ - 1} $, (b) 
${{t}_2} = 120\,{{\rm \omega} _{\rm L}}^{ - 1} $, and (c) 
${{t}_3} = 160\,{{\rm \omega} _{\rm L}}^{ - 1} $. The value of harmonic generated field in comparison with the laser pulse field is obvious in each position of this figure. Evidently, the generated field by harmonic emission has a higher amplitude in front of the laser pulse than the other regions of it. This could be due to weak laser fields in this region. Furthermore, it seems that the space charge effect, which achieves the separation of electrons and ions from each other, can prevent the recombination of electrons with ions behind the laser pulse. Because harmonic generation is ceased at high intensities, I > 1015 w/cm2, the energy conversion efficiency is highly affected by the pulse shape, that is, the conversion efficiency is higher at lower intensity regions of the laser pulse. In this way, as far as we are concerned, the total energy conversion efficiency cannot indicate the effectiveness of the process. Here, we give another measure of efficiency (local efficiency) based on the ratio of maximum harmonic field amplitude square, E max−h, to the corresponding local main field amplitude square, E LM, as:
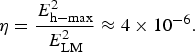$${\rm \eta} = \displaystyle{{E_{\rm h-\max} ^2} \over {E_{\rm LM}^2}} \approx 4 \times {10^{ - 6}}.$$Figure 4 shows the intensity spectrum of the generated fields in Figure 3. The spectrum consists of three parts: The first few harmonics, the plateau for intermediate orders, and the cutoff at the highest orders. Therefore, the general behavior of the present harmonic spectrum is similar to the previous theoretical and experimental works (Lewenstein et al., Reference Lewenstein, Balcou, Ivanov, L'Huillier and Corkum1994; Dionissopoulou et al., Reference Dionissopoulou, Mercouris and Nicolaides1996; Seres et al., Reference Seres, Seres, Verhoef, Tempea, Streli, Wobrauschek, Yakovlev, Scrinzi, Spielmann and Krausz2005; Murakami et al., Reference Murakami, Korobkin and Horbatsch2013) in lower intensity, 
${I} \approx {10^{14}} \ {\rm w}/{{\rm cm}^2}$. Based on the numerical calculation of the single atom model, it has been shown (Corkum, Reference Corkum1993; Schafer et al., Reference Schafer, Yang, DiMauro and Kulanderc1993) that the maximum photon energy, cut-off energy, that can be generated within this model is 
${{I}_{\rm p}} + 3.17\,{{U}_{\rm p}}$. Here, in order to have an order of cut-off energy for the generated harmonic, we calculate cut-off energy for the first cycle of the laser pulse (according to Fig. 3, it is evident that the most harmonic fields are formed in this area). As has been shown in Figure 4, the cut-off of this spectrum happens at a lower value 
${{I}_{\rm p}} + 1.32\,{{U}_{\rm p}}$. This difference can be explained by this reason that unlike the single atom model, the space charge (that causes all electron trajectories to be closed) and other collective effects in the field-ionized plasma can affect the harmonics generation process and shift of cutoff energy. It is worth mentioning that the low-order harmonics can be generated with oscillations of electrons density during the nonlinear process of field ionization (Andreev et al., Reference Andreev, Veisman and Chegotov2003). Because in the PIC simulation the whole feature of nonlinear effects is preserved, these types of harmonics are produced and added to the electric fields. Since the size of these fields is very small compared with the laser fields, they are not distinguishable. However, as mentioned in the previous section, the fields of the generated harmonics are calculated in a separate mesh by means of the artificial current j rec [Eq. (11)], which automatically separates the harmonic fields originated from the radiative recombination with the other fields (including harmonics caused by density oscillation) in plasma.
Fig. 3. The PIC simulation results for the laser electric field E y/E 0 (black curve) and the harmonic electric field E yh/E 0 (blue curve) for a 0 = 0.6 at (a) 
${{t}_1} = 40\,{{\rm \omega} _{\rm L}}^{ - 1} $, (b) 
${{t}_2} = 120\,{{\rm \omega} _{\rm L}}^{ - 1} $, and (c) 
${{t}_3} = 160\,{{\rm \omega} _{\rm L}}^{ - 1} $.
Fig. 4. The PIC simulation results of intensity spectrum for generated field presented in Figure 3 (with the same simulation parameters). The vertical and horizontal axes are corresponding to the square of normalized intensity and harmonic number (k/k L) respectively.
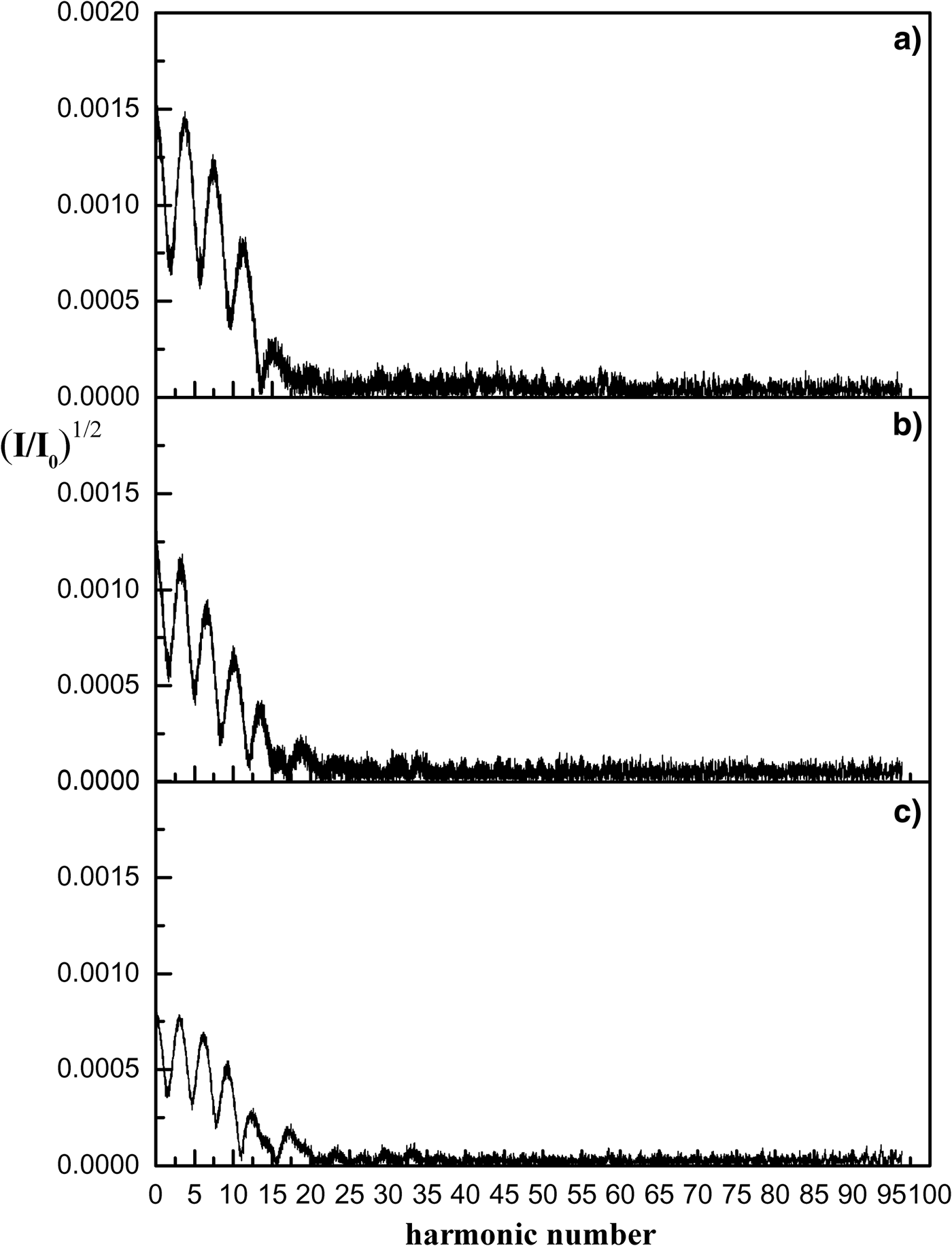
Figure 5 shows the intensity spectrum of harmonics generated by the amplitudes (a) a 0 = 0.5, (b) a 0 = 0.6, and (c) a 0 = 0.7 at 
${t} = 120\,{{\rm \omega} _{\rm L}}^{ - 1} $. It is evident that the intensity of harmonics is reduced by increasing the intensity of the pulse. This is due to the fact that the electron gains more energy in a strong laser field so that its trapping probability by the potential well of H ion is considerably reduced.
Fig. 5. The PIC simulation results for the harmonic intensity spectrum for (a) a 0 = 0.5, (b) a 0 = 0.6 and (c) a 0 = 0.7.
The initial velocity effect of the ionized electrons on the intensity spectrum is shown in Figure 6, for a pulse with the amplitude a 0 = 0.6 at 
${t} = 80\,{{\rm \omega} _{\rm L}}^{ - 1} $. In this figure, the red and black curves show the harmonic spectra for zero and nonzero initial velocity of electrons, respectively. It is clear that the harmonic spectrum is modified by changing the initial momentum of the ionized electrons, because the energy of the radiated photons depends on the electron energy. By comparing the red and black curves, it is realized that the general behavior of harmonic spectrum is not changed by choosing the nonzero initial momentum, but certain changes occur in the intensity of harmonics.
Fig. 6. The PIC simulation results for the harmonic intensity spectrum for a 0 = 0.6, (a) nonzero initial velocity of the ionized electrons (black curve), and (b) zero initial velocity of the ionized electrons (red curve).
Figure 7 shows the temporal evolution of the electromagnetic and mechanical energies. Time is given in units of laser cycles. Eventually, we come to the conclusion that the sum of electromagnetic and mechanical energies (total energy) is always constant, which confirms the accuracy and validity of our code.
Fig. 7. The PIC simulation results for the temporal evolution of the electromagnetic (red curve), mechanical (blue curve), and total (black curve) energy.
Additionally, the simulation result indicates that the present code can be used for the strict scrutiny of the plasma subjects, in which ionization plays an important role (Janulewicz et al., Reference Janulewicz, Grout and Pert1996; Ditmire, Reference Ditmire1996; Bauer, Reference Bauer2003; He & Chang, Reference He and Chang2005; Eslami & Basereh, Reference Eslami and Basereh2013; Misra et al., Reference Misra, Mishra, Sodha and Tripathi2014).
5. SUMMARY
In this paper, a novel algorithm based on the PIC simulation is introduced to investigate the radiative recombination during the ionization and formation of plasma when a non-relativistic laser pulse is passed through the hydrogen atoms. The theoretical and numerical expressions have been exploited for the ionization rate in consistence with the values of the electric field strength. In addition, according to Eq. (7) the Stark shift is considered for the ground state of atoms in the presence of the laser electric field. Despite the pervious codes (Janulewicz et al., Reference Janulewicz, Grout and Pert1996; Bruhwiler et al., Reference Bruhwiler, Dimitrov, Cary, Esarey, Leemans and Giacone2003; Kemp et al., Reference Kemp, Pfund and Meyer-ter-Vehn2004; Chen et al., Reference Chen, Cormier-Michel, Geddes, Bruhwiler, Yu, Esarey, Schroeder and Leemans2013), the nonzero initial momentum is assigned for the ionized electrons. In our code, two Monte Carlo packages have been added to the usual PIC scheme after the computation of the charge and current and before the integration of Maxwell equations to study the harmonic generation produced by the recombination of the ionized electron. The energy gain of electron recombination has been implemented by introducing an artificial recombination current to save the energy conservation law. This recombination current is vital to calculate the fields of generated harmonics in the separate meshes. In this way, the intensity spectrum of the generated harmonic fields is illustrated. The spectrum is similar to those produced in lower intensities, albeit with some evident differences are also observed. In addition, the initial momenta of the ionized electrons are likely to affect the harmonic spectrum because the energy of the radiated photons varies with the electron energy.
