INTRODUCTION
In many researches and applications of high-energy and high-power laser, such as inertial confinement fusion (ICF), the high intensity laser pulses will propagate over long paths in air, so the intensity-length product (intensity multiply transmission distance) could be very large, resulting in various serious nonlinear effects, such as stimulated rotational Raman scattering (SRRS) (Henesian et al., Reference Henesian, Swift and Murray1985; Herring et al., Reference Herring, Mark and William1986; Leung et al., Reference Leung, Oron, Klimek, Holmes and Flusberg1988; Ying et al., Reference Ying, Kessler, Armstrong and Lawrence1993; Wang et al., Reference Wang, Zhang, Han, Li, Zhou, Feng and Xiang2011; Omatsu et al., Reference Omatsu, Kong, Park, Cha, Yoshida, Tsubakimoto, Fujita, Miyanaga, Nakatsuka, Wang, Lu, Zheng, Zhang, Kalal, Slezak, Ashihara, Yoshino, Hayashi, Tokizane, Okida, Miyamoto, Toyoda, Grabar, Kabir, Oishi, Suzuki, Kannari, Schaefer, Pandiri, Katsuragawa, Wang, Lu, Wang, Zheng, He, Lin, Hasi, Guo, Lu, Fu, Gong, Geng, Sharma, Sharma, Rajput, Bhardwaj, Zhu and Gao2012), which limit the laser intensity and fluence that can be transmitted through the air. Therefore, the SRRS process suppression turns to be one of the key problems to be solved in the application and transmission of the high-energy and high-power laser. In 2004, Bordenave and Chies (Reference Bordenave and Chies2006) adopted the scheme that a part of transmission media of air is replaced with inert gas to increase the SRRS threshold distance (Kurnit et al., Reference Kurnit, Shimada and Sorem1987; Wegner et al., Reference Wegner, Auerbach, Biesiada, Dixit, Lawson, Menapace, Parham, Swift, Whitman and Williams2004), however, the method is costly to build and maintain. Wang et al. (Reference Wang, Zhang, Han, Li, Zhou, Feng and Xiang2011) proposed to use transmitting Bragg volume gratings to inhibit SRRS by filtering out the Stokes light, but the tiny SRRS frequency shift and high-intensity laser pulse bring a great challenge to grating fabrication.
Skeldon and Bahr (Reference Skeldon and Bahr1991) installed the smoothing by spectral dispersion (SSD) on the narrow line-width laser (351 nm) to study the SRRS process, the results showed the threshold of SRRS was increased compared to that of the narrow line-width laser, however, no detailed explanation and subsequent studies were reported.
SSD, which is usually used in laser-irradiation uniformity in far field (Boehly et al., Reference Boehly, Babushkin, Bradley, Craxton, Delettrez, Epstein, Kessler, Knauer, Mccrory, Mckenty, Meyerhofer, Regan, Seka, Skupsky, Smalyuk, Town and Yaakobi2000; Joshua et al., Reference Joshua1997; Miyaji et al., Reference Miyaji, Miyanaga, Urushihara, Suzuki, Matsuoka, Nakatsuka, Morimoto and Kobayashi2002; Matsushima et al., Reference Matsushima, Owadano, Matsumoto, Okuda, Tomie, Koyama, Staffin and Yano1993; Paul, Reference Paul2007; Skupsky et al., Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures1989; Zhang et al., Reference Zhang, Wang, Su, Liu, Tang, Liu, Jing and Zhang2010), will bring a great advantage to the design and building of the high-energy and high power laser system such as ICF drivers, if it can effectively suppress the SRRS process in near field.
In this paper, the mechanism of how SSD suppresses the effect of SRRS and the variation of SRRS gain with SSD parameters are studied in detail by simulation.
RELATED THEORIES
The governing Raman equations under the slowly varying envelop approximation are (Ying et al., Reference Ying, Kessler and George1992)
Where E L and E S are the laser and the Stokes complex amplitudes, and their wave numbers are k L and k S, respectively. Q represents the medium polarization, k 1, k 2, and k 3 are coupling coefficients, Γ is the Raman bandwidth. Eqs. (1a) and (1b) contain the influence of diffraction on laser and Stokes transmission.
SSD is achieved using electro-optic phase modulator and diffraction gratings, as Figure 1 shown (Skupsky et al., Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures1989). Grating 1, placing before the phase modulator, introduces a time delay to the initial narrow-line-width laser beam; the phase-modulator broaden the spectrum of the initial narrow-line-width laser; grating 2, setting behind the phase modulator, is used to compensate the phase delay induced by the grating 1, and impose angular spectral dispersion and transverse “colors” (frequency) cycling.

Fig. 1. Double gratings SSD sketch (The dotted lines are contours of constant color or frequency not wave fronts, and the “B” and “R” represent the high and the low frequency waves respectively) (Skupsky et al., Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures1989).
In the simulation, we only consider the variations of the physical quantities in the x direction considering the spatial symmetry of the laser beam. Using the slowly varying amplitude approximation, the complex amplitude of the electric field in SSD laser pulse can be written as (Skupsky et al., Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures1989)
where E L0(x, t) is the real amplitude of the laser electric field, φ0(x) is the transverse additional phase of the beam, δ and ν m are the modulation amplitude and frequency of the phase-modulator respectively, β = Δθ/Δλ is the grating dispersion coefficient, ν 0 is the laser central frequency.
In the ICF driver and other high-energy and high-power laser systems, the phases across the transverse direction of the beam are fluctuant and distorted due to numerous optical elements and thermal effects etc., so the additional phase φ0(x) is not a constant but a random distribution, which could be expressed as (Fu and Zhang, Reference Fu and Zhang2011; Williams et al., Reference Williams, Auerbam, Hunt, Lawson, Manes, Orth, Sacks, Trenholme and Wegner1997):
where
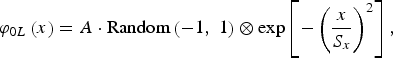 $${\rm \varphi} _{0L} \left(x \right)=A \cdot {\rm Random}\left({ - 1\comma \; 1} \right)\otimes \exp \left[{ - \left({\displaystyle{x \over {S_x }}} \right)^2 } \right]\comma$$
$${\rm \varphi} _{0L} \left(x \right)=A \cdot {\rm Random}\left({ - 1\comma \; 1} \right)\otimes \exp \left[{ - \left({\displaystyle{x \over {S_x }}} \right)^2 } \right]\comma$$Here, φ0L(x) and φ0H(x) represent the phase distortion of the low frequency and the high frequency respectively. The low frequency term φ0L(x) is a random Gaussian distribution, generated by convolving a Gaussian function with a uniformly distributed random number sequence. In Eq. (4), A is the low frequency phase amplitude coefficient, S x is the factor determining the size of phase distortion of the laser beam in the x direction. σ is disturbing amplitude of the high frequency random phase.
SIMULATION RESULTS AND ANALYSIS
Substituting the laser electric field Eq. (2) into coupled wave Eqs (1), we can get the variation of many physical parameters, such as waveform, intensity and energy of the laser, and the Stokes light. In the numerical simulation, the values of the physical parameters are respectively: the central wave length of the laser and the Stokes light are λL0 = 1053 nm, λs0 = 1061.5 nm, the corresponding gain coefficient is g = 2.7 cm/TW (Rokni & Flusberg, Reference Rokni and Flusberg1986), for the initial laser, both the temporal and the spatial distribution are 18-order super-Gaussian, the intensity is I L = 2 GW/cm2, the pulse full width is t L = 3 ns, the diameter of the beam is D = 10 cm, the parameters of additional phase distribution φ 0(x) are A = 1, S x = 5 cm, σ = 0.2. The generation threshold for SRRS is defined where the energy of the Stokes light reaches 1% of the energy of the initial laser; the corresponding transmission length is defined as threshold distance. For simplification, the size of divergence angle and the reduction of laser intensity caused by the divergence angle are neglected.
According to Eq. (2), the characteristics of SSD beam are determined mainly by the three parameters: the modulation amplitude δ, the modulation frequency ν m and the grating dispersion coefficient β, so the effect of SSD on the SRRS process is studied mainly base on the variation of the above three parameters.
The Stokes light conversion efficiency η varying with the propagation distance Z is simulated when the SSD parameters take different values, as shown in Figure 2. From Figure 2 it can be seen that: (1) with the increasing of the modulation amplitude δ, the modulation frequency ν m (GHz), and the grating dispersion coefficient β (mrad/nm), the SRRS threshold distances of the pulses 1, 2, 3, 4, 5, 6 increase gradually, respectively are 37.2 m, 38.2 m, 38.6 m, 43.7 m, 45.4 m, and 47.6 m. So, we can lower the SRRS gain to enlarge the threshold distance by amplifying the three SSD parameters above, and the modulation amplitude has the most influence. (2) The narrow line-width laser pulse 1 (δ = 0, ν m = 0, β = 0), without the impact of SSD, whose threshold distance of 37.2 m is the minimum of the six. Pulse 2 (δ = 1, ν m = 5 GHz, β = 0) is a normal nonlinear chirp laser pulse, without angular spectral dispersion and transverse “colors” (frequency) cycling, and its threshold distance of 38.2 m is longer than that of the pulse 1. It is proved that the SRRS gain of the narrow line-width laser pulse can be reduced by temporal phase modulation. The pulse 3 (δ = 1, ν m = 5 GHz, β = 0.5 mrad/nm) represents a SSD pulse as well as pulses of 4, 5, and 6, with the SRRS threshold distance of 38.6 m, longer than those of pulse 1 and pulse 2, which can be inferred that the introduction of transverse “colors” (frequencies) cycling can reduce the SRRS gain further. Therefore, compared with the narrow line-width laser pulse, the SRRS gain of the SSD beam is smaller as a result of the temporal and the spatial variations of the SSD pulse phase.

Fig. 2. The Stokes conversion efficiency η as a function of propagation distance Z.
It is defined that the average fluence modulation degree is the ratio of the sum of the fluence modulation degree (the ratio of the maximum to the mean of the fluence) every position to the transmission distance. For the six pulses above, their average fluence modulation degrees respectively are M a1 = 1.51, M a2 = 1.51, M a3 = 1.45, M a4 = 1.33, M a5 = 1.22, M a6 = 1.18 with the transmission path of 50 m (assume no SRRS generate). Evidently, the average fluence modulation degrees decrease gradually with the increasing of the SSD parameters. Comparing the pulses 1 with 2, noticing that the SRRS threshold distances Z th2 > Z th1 while average fluence modulation degree M a2 = M a1, it can be deduced that when the grating dispersion coefficient β = 0, the nonlinear temporal phase modulation to the laser reduce the Stokes gain coefficient without change the laser fluence modulation degree to decrease of the SRRS gain. Comparing the pulses 2 with 3, noticing that the SRRS threshold distances Z th3 > Z th2 while the average fluence modulation degree M a3 < M a2, it can be inferred that the reduction of the average fluence modulation degree because of the transverse “colors” cycling is the other reason for the decreasing of the SRRS gain for SSD laser.
To understand the influence of SSD on SRRS process, we separately simulate how the SSD parameters impact the laser average fluence modulation degree and the Stokes light energy conversion with the propagation distance of 45 m, as shown in Figure 3. The solid and the dotted curves represent the variations of the average value of the fluence modulation degree M a (assuming no Stokes generation) and the Stokes light energy conversion η respectively. In the practical applications, in order to ensure the high harmonic conversion efficiency, the grating dispersion coefficient must satisfy β ≤ 2 mrad/nm (Skupsky et al., Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures1989), also due to the limitation of modulator voltage, the modulation amplitude δ is relatively small, consequently in the simulation we take 0 ≤ δ ≤ 5, 0 ≤ ν m ≤ 15 GHz, and 0 ≤ β ≤ 2 mrad/nm.

Fig. 3. The variation of Stokes light conversion efficiency η and the laser average fluence modulation degree M a with (a) modulation amplitude δ(ν m = 10 GHz, β = 1.5 mrad/nm); (b) modulation frequency ν m(δ = 3, β = 1.5 mrad/nm), and (c) grating dispersion coefficient β(δ = 3, ν m = 10 GHz).
From Figure 3, it can be seen: (1) with the increasing of the modulation amplitude δ, the laser average fluence modulation degree M a decreases first with tiny fluctuations, followed with a slow climb trend. However, the laser average fluence modulation degrees M a decrease monotonically with the increasing of the modulation frequency ν m and the grating dispersion coefficient β, and their variation rules are similar. (2) The Stokes light energy conversions efficiency η appears declining in general as the increase of the SSD parameters, however, their variation ranges and rules are different: (a) the conversions efficiency η decreases overall with some tiny fluctuations as the increasing of the modulation amplitude δ; (b) with the increasing of the modulation frequency ν m, η decreases monotonically with a sharp drop firstly and finally reach the minimum slowly; (c) η decrease monotonically with the increase of the grating dispersion coefficient β, and the whole process vary slowly.
Figure 3a shows that the curve inflection points (or the variation trend) of the conversion efficiency η and the average fluence modulation degree M a are different, same in Figure 3b, which means that the variation rules of the Stokes light energy conversion and the laser average fluence modulation degree with the modulation amplitude or the modulation frequency are different, again proving that the laser average fluence modulation degrees and the Stokes gain coefficient are reduced simultaneously with the increasing of modulation amplitude or frequency for the SSD pulse. However, the curve inflection points (or the variation trend) of η and M a are similar in Figure 3c, which proves that their variation rules are similar, thus only the laser average fluence modulation degrees reduce while the Stokes gain coefficient unchanged with the increase of the grating dispersion coefficient. The reduction speed of the Stokes light energy conversion is faster than that of the laser average fluence modulation degrees with the increase of the grating dispersion coefficient, because SRRS is a nonlinear interaction.
The numerical simulation and theory analysis above demonstrate that SSD can reduce the SRRS gain as result of the decreasing of the laser modulation degree and the reducing of the Stokes gain coefficient with the increasing of the SSD parameters. It can be explained from two aspects as follows: First, the Stokes gain coefficient decreases owing to the temporal variation of the SSD laser phase. In the SRRS process, the optical phonons are so slow that it can be seen stationary compared to the laser and the Stokes light. Observing the SRRS process in a position of the transmission path, the phase of the SSD pulse varies periodically with time, so do the excited phonons. As a result, the phonons can't be amplified coherently, nor the Stokes light. Consequently the Stokes light gain coefficient is reduced. Second, the laser fluence modulation degree decreases due to the transverse color cycle. It can be considered that the cross section of the SSD beam each moment consists of different waves of periodicity instantaneous frequency, and there is a slight lateral movement between the same frequency waves of two adjacent moments, so the waves of the two adjacent moments can't overlap coherently, the fluence modulation degree of the SSD beam will be decreased.
In practical application and experiments, the SRRS threshold distance and the laser fluence modulation degree can be controlled by changing the SSD parameters above. For example, the SRRS threshold distance of 37.2 m of the pulse 1 in Figure 2 is expected to reach 45 m, the variation of the required minimum grating dispersion coefficient βmin with the modulation amplitude δ and the modulation frequency ν m was shown in the Figure 4a. It can be known from the Figure 4a that (1) there are many suitable values for the SSD parameters, which can satisfy the requirement above, and mainly concentrated in 1.5 ≤ δ≤ 5 and 3.5 GHz ≤ ν m ≤ 15 GHz. 2) The variations of the required minimum grating dispersion coefficient βmin with the modulation amplitude δ and the modulation frequency ν m are different. For certain frequency modulation ν m, the required minimum grating dispersion coefficient βmin doesn't vary monotonously with the increasing of the modulation amplitude δ; while, if the modulation amplitude δ is invariant, the required minimum grating dispersion coefficient βmin generally decreases monotonously with the increasing of the modulation frequency ν m. Generally, for the large-scale laser system, the fluence modulation degree is relatively large. To our knowledge and experience, it is good enough if the fluence modulation degree is not more than 1.4. Figure 4b shows the variation of the required minimum grating dispersion coefficient βmin with the modulation amplitude δ and the modulation frequency ν m when M a ≤ 1.4 with the transmission path of 45 m (assume no SRRS generation). Figure 4b shows the variation of the required minimum grating dispersion coefficient βmin with the modulation amplitude δ and the modulation frequency ν m, which are different from those of in Figure 4a, the required minimum grating dispersion coefficient βmin decrease monotonously with the increasing of the modulation amplitude δ and the modulation frequency ν m.

Fig. 4. (a) Set the threshold distance Z th = 45 m and (b) set the average fluence modulation degree M a ≤ 1.4, the variation of the required minimum grating dispersion coefficient βmin with the increase of the modulation amplitude δ and the modulation frequency ν m.
CONCLUSIONS
In this paper, the suppression mechanisms of SSD on SRRS process and the influence of the SSD parameters on the Stokes light gain are investigated by numerical simulation and theoretical analysis. It is demonstrated that SSD can reduce not only the Stokes light gain coefficient but also the laser fluence modulation degree, which is attributed to the temporal and spatial periodical change of the SSD pulse phase, thus the SRRS gain of the SSD pulse is reduced. For engineering applications, it is valuable to use SSD to suppress the SRRS process and consequently lengthen the SRRS threshold distance for the high-energy and high-power laser system, the relevant method and the simulation results are presented.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China (Grant No. 61138005 and 61008004), RFDP20102302120034, and the Fundamental Research Funds for the Central Universities (Grant No. HIT. KLOF. 2010035).






