1. INTRODUCTION
There are a number of nonlinear effects in intense laser and plasma interaction, which are related to the ponderomotive force (Kaw et al., Reference Kaw, Schmidt and Wilcox1973), collisional nonlinearity (Shoda et al., Reference Shoda, Ghatak and Tripathi1976), relativistic effect (Kane & Hora, Reference Kane and Hora1981), and external magnetic field (Sadighi-Bonabi & Etehadi-Abari, Reference Sadighi-Bonabi and Etehadi-Abari2010), etc. Because of the important influence on inertial confinement fusion and particle acceleration, etc. (Esarey et al., Reference Esarey, Schroeder and Leemans2009; Rocca et al., Reference Rocca, Shlyaptsev, Tomasel, Gortazer, Hartshorn and Chilla1994), the nonlinear effects have been widely researched.
In the nonlinear effects, due to electromagnetic field, plasma density, and temperature have important influence on laser-plasma interaction, and their distribution and influence have been a research hotspot (Xia & Xu, Reference Xia and Xu2013; Harilal et al., Reference Harilal, Bindhu, Issac, Nampoori and Vallabhan1997; Xia et al., Reference Xia, Cai and Yi2011a; Reference Xia, Qin, Xu and Cai2011b). In theoretical researched works, Qiao et al. (Reference Qiao, He and Zhu2005) have discussed the magnetic-field profile and plasma density cavitation in intense laser-plasma interaction and found they depend on the laser intensity. Xie et al. (Reference Xie, Wu, Wang, Wang and Yu2007) have analyzed the electromagnetic fields and electron acceleration in the bubble regime of the laser-plasma interaction. Theobald et al. (Reference Theobald, Häbner, Kingham, Sauerbrey, Fehr, Gericke, Schlanges, Kraeft and Ishikawa1999) have investigated electron densities, temperatures, and the dielectric function of femtosecond-laser-produced plasmas experimentally and theoretically. Taking into account the ponderomotive force, Shokri and Niknam (Reference Shokri and Nikanm2006) have investigated the profile of the electric, magnetic field, and electron density in collisionless unmagnetized non-isothermal plasma. Abedi et al. (Reference Abedi, Dorranian, Abari and Shokri2011), and Abari & Shokri (Reference Abari and Shokri2011) have analyzed nonlinear heating and relativistic effect on the nonlinear structure of laser and plasma in collisional underdense plasma. Recently, Niknam et al. (Reference Niknam, Hashemzadeh and Shokri2009; Reference Niknam, Milani, Bokaei and Hashemzadeh2014) have studied weakly relativistic and ponderomotive effects on the density steepening in the interaction of an intense laser pulse with an underdense plasma. Panwar et al. (Reference Panwar, Ryu and Kumar2013) have investigated the effect of plasma channel non-uniformity on resonant third harmonic generation, and found that density ripple would affect harmonic generation. Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) have studied strong terahertz radiation generation in a rippled density magnetized plasma, and attained that density ripple would lead to THz generation. These recent research shows that there is present some interesting and novel nonlinear phenomenon in laser and plasma with density ripple.
In experimental research, Borghesi et al. (Reference Borghesi, Schiavi, Campbell, Haines, Willi, Mackinnon, Patel, Galimberti and Gizzi2003) have applied the proton imaging technique to detect and discuss the electric field distribution in laser-produced long-scale plasmas of inertial confinement fusion interest. Harilal et al. (Reference Harilal, Bindhu, Issac, Nampoori and Vallabhan1997) have observed electron density and temperature measurements in a laser produced carbon plasma. Goldsmith et al. (Reference Goldsmith, Seely, Feldman, Behring and Cohen1985) have estimated the average values of the electron temperature T e and the electron density N e in the corona plasmas of spherically irradiated high-Z targets. Oh et al. (Reference Oh, Uhm, Kang, Lee and Suk2010) have detected temporal evolution of electron density and temperature in capillary discharge plasmas. Lancia et al. (Reference Lancia, Grech, Weber, Marquès, Romagnani, Nakatsutsumi, Antici, Bellue, Bourgeois, Feugeas, Grismayer, Lin, Nicolai, Nkonga, Audebert, Kodama, Tikhonchuk and Fuchs2011) have diagnosed electrostatic fields in high-power, nanosecond laser pulse with underdense plasma by proton radiography and used a current three-dimensional wave propagation code equipped with nonlinear and nonlocal hydrodynamics to simulate electron density and temperature and compare the experimental results. In some experiment of laser-target, quasi-periodic rippled plasmas have been observed (Sheng et al., Reference Sheng, Zhang and Umstadter2003; Kuo et al., Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007), the plasma has an inhomogeneous density profile. Due to some novel and potential applications, the research of laser and rippling plasma interaction has been quickly developed. Recently, some research results have showed that periodic plasma density structure can affect phase matching (Kaur et al., Reference Kaur, Yadav and Sharma2010), direct acceleration (York et al., Reference York, Milchberg, Palastro and Antonsen2008), stimulated Raman scattering (Jha et al., Reference Jha, Singh, Upadhyaya and Mishra2008) and so on.
In spite of great achievement in nonlinear structure of electromagnetic wave and plasma, so far we have not formed an impressed analysis of electromagnetic field, electron temperature, and electron density in laser-plasma interaction. The previous lots research works of nonlinear effects mainly focus on homogeneous plasma, while the nonlinear structure of electromagnetic wave and plasma has received relatively less attention in relativistic laser and inhomogeneous plasma interaction. Especially, the periodic rippled plasma is a novel and special plasma. In papers based on our previous investigation (Xia & Xu, Reference Xia and Xu2013) and Niknam et al. (Reference Niknam, Hashemzadeh and Shokri2009; Reference Niknam, Milani, Bokaei and Hashemzadeh2014), we investigated the influence of relativistic, ohmic heating, and plasma ripple on electromagnetic field, electron temperature and electron density in interaction of relativistic laser and plasma with density ripple. In the case, plasma is assumed as collisional underdense rippled plasma, laser flux is on the order of I ≈ 1018 W × cm−2, laser wavelength is 0.8 µm, the initial electron density is a periodic rippled plasma n e0/n e00 = (1 + B cos kz) and n e00 is taken to be 1.5 × 1021 cm−3, the critical density n c = 1.72 × 1022 cm−3.
2. BASIC THEORY MODEL AND FORMULATIONS
The present model is setup in a relativistic regime in non-isothermal, underdense, collisional, non-magnetized, and rippled plasma. In this model, a linear polarized electromagnetic wave, i.e., laser pulse of the form 
$E\lpar z\comma \; t\rpar = \hat xE\lpar z\rpar \exp \lpar - i{\rm \omega} _0 t\rpar $ with angular frequency ω0 propagates in the +z direction in vacuum. The electromagnetic wave enters plasma slab normally, and the wave equation governing the beam electric vector in plasmas can be written as
$$\nabla ^2 \vec E - \nabla \lpar \nabla \cdot \vec E\rpar + \displaystyle{{{\rm \omega} _0^2 } \over {c^2 }}{\rm \varepsilon} \vec E = 0.$$The electric intensity distribution of a high power Gaussian laser beam is expressed as
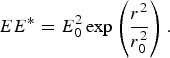$$EE^{\ast} = E_0^2 \exp \left( \displaystyle{{{r}^2 } \over {r_0^2}}\right).$$Where r 0 is the initial beam width, r is the radial component in cylindrical coordinate system, and E 0 is the axial amplitude of the beam. If density scale heights are much longer than Debye length λD and the atoms are highly ionized, then in thermal equilibrium at plasma temperature T the equilibrium density is (Kaur et al., Reference Kaur, Yadav and Sharma2010)
$$N = N_e \approx N_i \approx N_{0e} \exp \left( - \displaystyle{{{\rm \phi} _p } \over {2T}}\right).$$Where ϕp is the relativistic ponderomotive potential. In interaction of relativistic intensity laser (I ≥ 1018W/cm 2) and plasma, following Brandi et al. (2008) researched results, and giving relativistic ponderomotive force
$$F_p = - m_0 c^2 \nabla \lpar {\rm \gamma} - 1\rpar = - e\nabla \left[ \displaystyle{{m_0 c^2 } \over e}\lpar {\rm \gamma} - 1\rpar \right] = - e\nabla {\rm \phi} _p\comma \;$$
where γ = (1 + a 2/2)1/2 is relativistic factor, and a = eE/mω0c is laser intensity. The ponderomotive force pushes the electrons radially outwards creating a space charge field 
$\vec E_s = - \nabla {\rm \phi} _s$. In the quasi-steady-state ϕs = −ϕp, the ion motion is important for time scale greater than ωpi−1. Here we restrict ourselves for pulses of duration <ωpi−1. Using this in the Poisson's equation, ∇2ϕs = 4π(n e − n ′e0), one may write the modified electron density as
$$n_e = n_{e0} + \displaystyle{1 \over {4{\rm \pi} }}\nabla ^2 {\rm \phi} _s$$For inhomogeneous plasma, the nonlinear medium is a medium in which the charge density is non-uniform in space. The charge density variation is complex and depends on the type of plasma. In axial inhomogeneous plasma, the electron density changes along axial direction (z–axis) only. For such type of inhomogeneity, the electron density is written as n e0 = n e00D(Z). Where D(Z) the density ramp function is dependent on z coordinate only, and n e00 is equilibrium plasma density in the absence of laser beam. In the paper, initial plasma n e0 is assumed axial inhomogeneous plasma with a periodic density ripple
$$n_{e0} = n_{e00} \lpar A + B\cos kz\rpar$$Where k is wave number of rippled plasma, A and B express the rate of electron density and initial electron density, and the plasma rippled parameter, respectively. According to previous work (Xia & Xu, Reference Xia and Xu2013), electron density and electron frequency meets n e/n e00 = ωp2/ωp02, where ωp0 is electron plasma frequency in the absence of laser beam.
We assume an underdense plasma (with permittivity ε) occupying the space between z = 0 and the critical density surface in the interaction of a high-frequency electromagnetic field wave with a solid. The semi-space z < 0 is vacuum with permittivity εV = 1. The wave propagation is in the z direction. In this case, magnetic field of the pulse can be deduced from Faraday's induction law as follows:
$$\displaystyle{{\partial E_x } \over {\partial z}} = \displaystyle{{i{\rm \omega} } \over c}B_y.$$The laser imparts oscillatory to electron when laser propagates through the plasma
$$\vec v_{{\rm \omega} \comma k} = \displaystyle{{e\vec E} \over {im{\rm \gamma} {\rm \omega} _0 }}.$$The permittivity of plasma may be written as
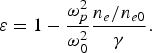$${\rm \varepsilon} = 1 - \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \omega} _0^2 }}\displaystyle{{n_e /n{}_{e0}} \over {\rm \gamma} }.$$The dielectric function of relativistic collisional plasma can be calculated by using the linearized force equation for the plasma electron fluid.
$$\displaystyle{{\partial \vec u} \over {\partial t}} = - \displaystyle{e \over {{\rm \gamma} m_0 }}\vec E - {\rm \nu} _e \vec u$$ In which e and 
$\vec u$ are the electron electrical charge and velocity. m 0 is the mass of electrons in the absence of electric field and νe is the collisional frequency which describes electron scattering by ions. Since the field varies harmonically with time. 
$\vec u$ can be written as
$$\vec u = - \displaystyle{{ie\vec E} \over {{\rm \gamma} m{}_0\lpar {\rm \omega} _0 + i{\rm \nu} _e \rpar }}.$$ With substituting 
$\vec u$ from Eq. (11) in the plasma electron current density equation 
$\vec J = - ne\vec u$, and using 
$\vec J$ in the Ampere's law, the dielectric function of a collisional relativistic plasma can be found as
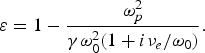$${\rm \varepsilon} = 1 - \displaystyle{{{\rm \omega} _p^2 } \over {{\rm \gamma} {\rm \omega} _0^2 \lpar 1 + i{\rm \nu} _e /{\rm \omega} _0 \rpar }}.$$ When the time duration of electromagnetic pulse is longer than the temperature relaxation time in plasma, Ohmic heating of electrons should be taken into account. The rate of electron heating (Ohmic heating) can be found from the component of 
$\vec u$ in phase with 
$\vec E$ as 
$ - e\vec E^{\ast} \vec u/2$.
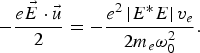$$- \displaystyle{{e\vec E \cdot \vec u} \over 2} = - \displaystyle{{e^2 \left\vert {E^{\ast} E} \right\vert v_e } \over {2m_e {\rm \omega} _0^2 }}.$$ To solve Eq. (13), we have to take into account the role of density and temperature fluctuation in ωp. When the time duration of electromagnetic pulse is longer than the temperature relaxation time in plasma, ohmic heating of electrons should be taken into account. The rate of electron heating can be found from the component of 
$\vec u$ in phase with 
$\vec E$ as 
$ - e\vec E^{\ast} \vec u/2$. In the steady state, this rate is balanced by the power loss via thermal conduction and collisions with ions and neutrals in the form of kinetic ohmic heating equation for electrons as
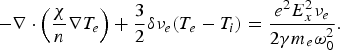$$- \nabla \cdot \left( \displaystyle{{\rm \chi} \over n}\nabla T_e \right) + \displaystyle{3 \over 2}{\rm \delta} {\rm \nu} _e \lpar T_e - T_i \rpar = \displaystyle{{e^2 E_x^2 {\rm \nu} _e } \over {2{\rm \gamma} m_e {\rm \omega} _0^2 }}.$$Here, χ/n = V th2/νe in which V th is the thermal velocity of plasma electron and δ = 2m e/m i = 2γm 0/m i is the mass ratio of electron to ions. If the collision time between plasma electrons is smaller than the conduction time, the first term in the left hand side of Eq. (5) is negligible in comparison with the second term and the electron temperature in plasma can be found as
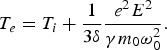$$T_e = T_i + \displaystyle{1 \over {3{\rm \delta} }}\displaystyle{{e^2 E^2 } \over {{\rm \gamma} m_0 {\rm \omega} _0^2 }}.$$On the other hand, we can use the momentum transfer equation in the stationary state for longer laser pulse duration. If the density gradient scale is larger than the Debye length, we can neglect the space charge force in comparison with the ponderomotive force and the electron pressure gradient force. In this case,
$$n_e F_p = - \nabla p_e = \nabla \lpar n_e T_e + n_i T_i \rpar.$$The relativistic form of ponderomotive force which acts on plasma electrons and modifies their density should be used in Eq. (11).
After neglecting the space charge force in the momentum transfer equation for the stationary state, we have
$$- m_0 n_e c^2 \nabla \lpar {\rm \gamma} - 1\rpar = \nabla \lpar n_e T_e + n_i T_i \rpar.$$By assuming the quasi neutrality condition, n e = n i, when ion temperature is constant, and by substituting Eq. (11) in Eq. (14), the electron density distribution can be calculated as
$$n_e = \displaystyle{{n_{e0} e^2 } \over {\left[ 1 + \displaystyle{1 \over {6{\rm \delta} {\rm \gamma} T_i }}\displaystyle{{e^2 E^2 } \over {m_0 {\rm \omega} _0^2 }}\right] ^{1 + 3{\rm \delta} } }}.$$Finally, by using n e from Eq. (18) in ωp of Eq. (12) for the nonlinear equation of wave propagation, we have
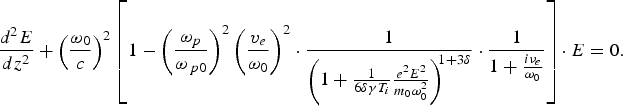$$\eqalign{& \displaystyle{{d^2 E} \over {dz^2 }} + \left( \displaystyle{{{\rm \omega} _0 } \over c}\right) ^2 \left[ 1 - \left( \displaystyle{{{\rm \omega} {}_p} \over {{\rm \omega} _{\,p0} }}\right) ^2 \left( \displaystyle{{v_e } \over {{\rm \omega} _0 }}\right) ^2 \cdot \displaystyle{1 \over {\left( 1 + \textstyle{1 \over {6{\rm \delta} {\rm \gamma} T_i }}\textstyle{{e^2 E^2 } \over {m_0 {\rm \omega} _0^2 }}\right) ^{\!\!1 + 3{\rm \delta} } }} \cdot \displaystyle{1 \over {1 + \textstyle{{i{\rm \nu} _e } \over {{\rm \omega} _0 }}}}\right]\! \cdot E = 0.}$$In Eq. (19), the plasma ripple, ohmic heating and relativistic nonlinearity effect the propagation of laser pulse in plasmas.
3. RESULTS AND DISCUSSION
In the present analysis, to find the profile of electromagnetic field of laser pulse in the plasma, the nonlinear differential Eqs. (19) and (7) is solved. In the numerical simulation, β = m e0c 2/T i is taken to be 1, and the normalized collision frequency νe/ω0 is kept constant at 0.01. Figure 1 presents the profile of electromagnetic field as a function of normalized plasma length ξ = zω0/c at a = eE/m 0cω0 = 1. Compared with the previous investigation (Abedi et al., Reference Abedi, Dorranian, Abari and Shokri2011), electromagnetic field presents some similar properties, such as, due to the influence of relativistic ponderomotive and ohmic heating, the field profiles becomes obvious nonlinear and non-sinusoidal. However, in the case, due to add the influence of plasma density ripple, electromagnetic field presents some new interesting phenomenon. First, they show obvious oscillation along plasma length rather than stabilization amplitude in homogeneous plasma. Obviously, the plasma ripple directly leads to the oscillation variation. In addition, the peak of electric and magnetic field are out of sync, in fact, the formation of the peak of magnetic field is little later than electric filed. They show that electromagnetic filed present stronger nonlinear variation in rippled plasma than homogeneous plasma.
Fig. 1. Normalized electromagnetic field of laser pulse in rippled plasma when a = 1, n e0/n e00 = (A + Bcoskξ) (A = 1, B = 0.5, k = 1).
In Figure 2, the profiles of electric and magnetic fields are plotted as a function of ξ = zω/c in various rippled plasma. It is clearly observed that, with the increasing laser intensity, the amplitude of electric and magnetic fields is obvious increased, and wavelength of fields is decreased slightly. Since the laser intensity is proportional to the square of amplitude, which brings a marked variation of amplitude. While increasing laser intensity leads to increasing the plasma electron density perturbation. In this case, the dielectric function of plasma is decreased, and consequently, the wavelength of electromagnetic field is decreased. In addition, electromagnetic field profile shows obvious oscillation along plasma length, with the increase of B and k, the amplitude oscillation of fields strengthened significantly, and their anti-synchronism also increase. For the parameters of B and k, the influence of k is more obvious than the parameter B. It presents that the plasma ripple can obvious affect the profile of electric and magnetic field and increases their instability propagation in the plasma.
Fig. 2. Normalized electric field (a, b, and c) and magnetic field (d, e, and f) of laser pulse in various rippled plasma when a = 1 (red), a = 2 (blue) and a = 3 (green), the rippled plasma parameter: A = 1, B = 0.25, k = 1 (a, d), A = 1, B = 0.5, k = 1 (b, e) and A = 1, B = 0.5, k = 1.5 (c, f).
In the interaction of laser pulse with relativistic underdense collisional plasma, change in the intensity of laser pulse leads to change in the temperature and density profiles of plasma. By using E in Eqs. (6) and (10), variation of plasma electron normalized temperature T e/T i and normalized density n e/n e0 for a 0 = 1, 2, 3 are shown in Figure 3. It is noted that, with the increase of laser intensity, the oscillation of the electron temperature and density become highly peaked, their oscillation amplitude increases and at the same time their wavelength decreases. In addition, due to add the influence of plasma density ripple, electron temperature and density profile shows obvious oscillation along plasma length rather than stabilization amplitude envelope in homogeneous plasma. With the increase of B and k, oscillation amplitude of electron temperature and density increase, and their anti-synchronism also increase, for the parameters of B and k, the influence of k is more obvious than the parameter B.
Fig. 3. Normalized electron temperature and electron density as a function of plasma length in various rippled plasma when a = 1 (red), a = 2 (blue) and a = 3 (green), the rippled plasma parameter: A = 1, B = 0.25, k = 1 (a), A = 1, B = 0.5, k = 1 (b), and A = 1, B = 0.5, k = 1.5(c).
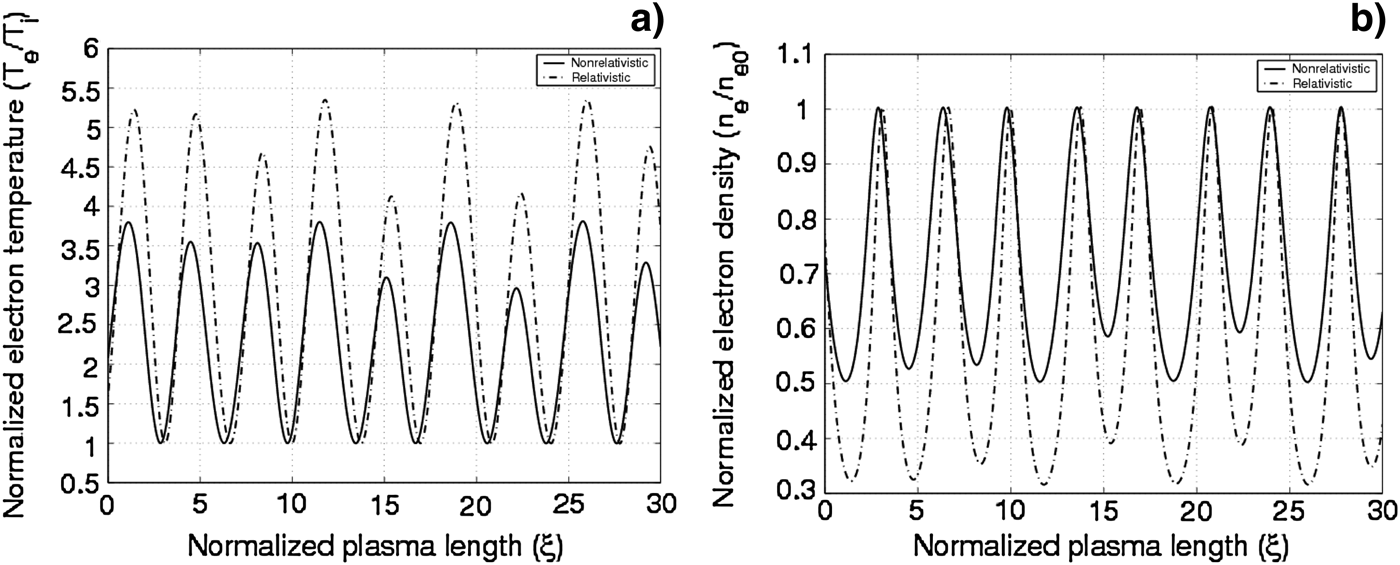
A comparison is done between the normalized plasma electron temperature and normalized plasma electron density in non-relativistic regime of plasma and relativistic regime of plasma when γ varies with E at a 0 = 2, which is illustrated in Figure 4. Large difference of electron temperature and density in the relativistic and nonrelativistic regimes of plasma, which is shown in Figure 4, it is clearly seen that relativistic effect strengthen nonlinear ponderomotive force and increase electron temperature, and further decrease electron density. In addition, the distribution of extremums of electron temperature and density are not synchronized in relativistic and nonrelativistic case. Compared with nonrelativistic case, their distribution presents a red shift, i.e., the wavelength of electron temperature and density oscillations increase. In fact, the difference between these two curves arises from taking into account the relativistic effect in the calculations. Electron bunches become narrower, since they experience a more intense ponderomotive force, and lead to the interesting nonlinear phenomenon.
Fig. 4. Normalized electron temperature and electron density of relativistic plasma (Dash-dot line) and nonrelativistic plasma (solid line) when a = 2, the rippled plasma parameter: A = 1, B = 0.5, k = 1.
4. CONCLUSION
In this work, nonlinear structure of electromagnetic field, electron temperature and electron density in interaction of ultra-intense laser and collisional underdense rippled plasma is investigated. Plasma is taken to be non-isothermal, collisional effect and density ripple is taken into account. We obtained the nonlinear differential and integral equation for the electromagnetic field, then we found the electron temperature and density distribution in the plasma. By numerical method, we plotted the electromagnetic field, electron temperature and electron density variation profiles versus z for the different values of the maximum electron density and laser energy flux. Results show that in the case, relativistic and ohmic heating lead to the nonlinear structure of electromagnetic field, electron temperature and electron density, which the field profiles becomes obvious nonlinear and non-sinusoidal due to the influence of relativistic ponderomotive and ohmic heating, and electron temperature and density profile become highly peaked. However, due to the influence of plasma density ripple, compared with homogenous plasma, electromagnetic field, electron temperature and electron density present obvious oscillation along plasma length rather than stabilization amplitude, and their peak are out of sync.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Science Foundation of China (Grant Nos. 11364010, 11147194, 11347015) and Scientific Research Foundation of Guilin University of Technology (Grant No. 002401003390) and Guangxi Universities Scientific Research Project.
