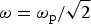Introduction
Anomalous absorption and scattering of laser by nanoparticles, clusters, and nanotubes is a subject of significant interest. Surface plasmon resonance plays an important role in these processes and gives rise to the phenomenon of surface enhanced Raman scattering (Phipps et al., Reference Phipps, Zhigilei, Polynkin, Baumert, Sarnet, Bulgakova, Bohn and Reif2014; Yoneda et al., Reference Yoneda, Inubushi, Yabashi, Katayama, Ishikawa, Ohashi, Yumoto, Yamauchi, Mimura and Kitamura2014). Intense short-pulse laser interaction with deuterium clusters gives rise to ion Coulomb explosion and high yield neutron production (Ditmire et al., Reference Ditmire, Zweiback, Yanovsky, Cowan, Hays and Wharton1999; Liu and Tripathi, Reference Liu and Tripathi2003). Anharmonic clusters, embedded in gases, are efficient generators of laser harmonics (Kumar and Tripathi, Reference Kumar and Tripathi2013). Amendola et al. (Reference Amendola, Rizz, Polizz and Meneghetti2005) have found that gold nanoparticles, synthesized by laser ablation of gold plate in toluene, do not show their characteristic surface plasmon absorption due to a graphitic matrix. Ahmad and Tripathi (Reference Ahmad and Tripathi2006) have shown strong absorption of laser normally incident on a metal surface embedded with nanoparticles when the laser frequency approaches the frequency of surface plasmon oscillations. Thareja and Sharma (Reference Thareja and Sharma2006) have reviewed the physical effects on metallic surface by high-power ration. Pustovalov (Reference Pustovalov2004) studied the heating of spherical solid metal particles by a laser pulse. Kumar and Verma (Reference Kumar and Verma2011) have found that 40% reduction in metal reflectivity with radius r np0 ≈ 50 Å of single layer of nanoparticles placed at distance 
$d \,{\sim}\, 10r_{{\rm n}{\rm p}_0}$ for a p-polarized infrared laser.
Hwang et al. (Reference Hwang, Vorobyev and Guo2009) have studied reflectivity reduction of metals due to an increase in the effective surface area by the presence of nanorods. It has been observed experimentally that laser absorption occurs due to nanorods over dielectric surfaces, revealing that the nanostructures provide stronger laser–material coupling. Nanorod suspensions in liquids show optical constraining properties (Link et al., Reference Link, Burda, Nikoobakht and El-Sayed2001). Deepika et al. (Reference Deepika, Chauhan, Varshney, Singh and Sajal2015) have studied the effect of static magnetic field on surface plasmon resonance in nanoparticles. Burakov et al. (Reference Burakov, Bulgakova, Stoian, Mermillod-Blondin, Audouard, Rosenfeld, Husakou and Herte2007) have observed laser-induced changes in dielectric properties in transparent materials. Bendib (Reference Bendib2017) has studied kinetic effects and found that collisional heating in the non-linear regime leads to velocity space anisotropy in electron distribution.
In the current paper, we study the nonlinear absorption of laser over a dielectric surface in the presence of metallic nanorods. The laser imparts oscillatory velocity to nanorod electrons that acquire resonantly a large value at surface plasmon resonance. The collisions randomize the drift momentum and give rise to power dissipation from the laser. At high laser intensity, the electron temperature rises significantly and nanorods undergo expansion and adiabatic cooling. This leads to reduction in plasmon frequency. In an initially over dense (having 
${\rm \omega} _{\rm p} \gt {\rm \omega} \sqrt 2 $), the surface plasmon resonance can be observed in the expansion phase.
In the section “Laser absorption with nonexpanding nanoroads”, we study the linear absorption of normally impinged laser over a dielectric surface having non expanding nanorods. In the section “Nonlinear absorption with expanding nanoroads”, we study the nonlinear power absorption in expanding nanorods. The results are discussed in the section “Discussion”.
Laser absorption with nonexpanding nanoroads
Consider a dielectric (z > 0) of refractive index η, embedded by a layer of metallic nanorods of length l, radius 
$r_{n_0}$, free electron density 
$n_0^0 $, and relative lattice permittivity εL aligned along 
$\hat y$. The inter-rod separation is d (Fig. 1). A laser is normally impinged on the surface with electric field:
$$\vec E_{\rm i} = \hat xE_0e^{ - ({\rm \omega} t - {\rm \omega} z/c)}$$
Fig. 1. Schematic of normal incident laser over a dielectric surface embedded with nanorods.
The field of the laser reflected from the dielectric may be written as
$$\vec E_{\rm R} = \hat xR_{\rm A}E_0e^{ - ({\rm \omega} t + {\rm \omega} \eta z/c)}$$whereas the laser field inside the dielectric as
$$\vec E_{\rm T} = \hat xT_{\rm A}E_0e^{ - ({\rm \omega} t - {\rm \omega} \eta z/c)}$$where R A and T A are the amplitude reflection and transmission coefficient's deduced below.
At z = 0, the auxiliary magnetic field of the laser undergoes a jump.
Using 
$\vec \nabla \times \vec H = \vec J + \displaystyle{{\partial \vec D} \over {\partial t}}$ or 
$\oint {\vec H \cdot d\vec l = \int {\lpar {\vec \nabla \times \vec H} \rpar }} \cdot d\vec S$, one may deduce the jump condition:
$$H_{y_{{\rm II}}} - H_{y_{\rm I}} = - J_{{\rm S}_{\rm X}}$$
where 
$H_{y_{\rm I}} = \displaystyle{{A_0} \over {c{\rm \mu} _0}}e^{ - i({\rm \omega} t - {\rm \omega} z/c)}$, 
$H_{y_{{\rm II}}} = T_{\rm A}\displaystyle{{A_0} \over {c{\rm \mu} _0}}\eta e^{ - i({\rm \omega} t - {\rm \omega \eta} z/c)}$, 
$J_{{\rm S}_{\rm X}} = - n_0ev_{\rm X}{\rm \pi} r_{n_0}^2 l$ and 
$v_{\rm X} = {\rm \beta} E_{\rm T} = {\rm \beta} T_{\rm A}E_{\rm I}$
where β is the electron mobility deduced below.
$$\eqalign{\lpar {1 - R_{\rm A}} \rpar \displaystyle{{A_0} \over {c{\rm \mu} _0}} & = T_{\rm A}\displaystyle{{A_0} \over {c{\rm \mu} _0}}{\rm \eta} + J_{{\rm S}_{\rm X}} \cr & = T_{\rm A}\displaystyle{{A_0} \over {c{\rm \mu} _0}}{\rm \eta} - n_0e{\rm \beta \pi} r_{n_0}^2 lT_{\rm A}A_0}$$
$$\lpar {1 - R_{\rm A}} \rpar = T_{\rm A}({\rm \eta} - e{\rm \beta \pi} r_{n_0}^2 lc{\rm \mu} _0)$$
$$\lpar {1 + R_{\rm A}} \rpar = T_{\rm A}$$
$$T_{\rm A} = \displaystyle{2 \over {1 + {\rm \eta} - \displaystyle{{e{\rm \beta \pi} r_{n_0}^2 l} \over c}}},\quad R_{\rm A} = \displaystyle{{1 - {\rm \eta} + \displaystyle{{e{\rm \beta \pi} r_{n_0}^2 l} \over c}} \over {1 + {\rm \eta} - \displaystyle{{e{\rm \beta \pi} r_{n_0}^2 l} \over c}}}$$The electric field inside the nanorod is
$$\vec E_{\rm T} = \vec E_{\rm i} + \vec E_{\rm R} = \hat xT_{\rm A}E_0e^{ - {\rm \omega} t}$$The electron excursion under this field is governed by the equation of motion
$$\displaystyle{{\partial ^2\vec \Delta} \over {\partial t^2}} + \displaystyle{{{\rm \omega} _{\rm p}^2} \over 2}\vec \Delta = \displaystyle{{ - e{\vec E}_{\rm T}} \over m} - {\rm \nu} \displaystyle{{\partial \vec \Delta} \over {\partial t}}$$
where 
${\rm \omega} _{\rm p}^2 = (n_0^0 e^2/m{\rm \varepsilon} _0)$, ν is the electron ion collision frequency.
By substituting ∂/∂t = −iω, we obtain from Eq. (8) the excursion 
$\overrightarrow \Delta $ and velocity of electron 
$\overrightarrow v = \partial \overrightarrow \Delta /\partial t$,
$$\overrightarrow \Delta = \displaystyle{{(e{\overrightarrow E} _{\rm T})/m} \over {\left[ {\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right) + i{\rm \nu \omega}} \right]}}e^{ - i{\rm \omega} t}$$and
$$\overrightarrow {\rm \nu} = \displaystyle{{d\overrightarrow \Delta} \over {dt}} = {\rm \beta} \overrightarrow E _{\rm T} = \displaystyle{{\lpar { - i{\rm \omega}} \rpar \lpar {eE_0T_{\rm A}} \rpar /m} \over {\left[ {\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right) + i{\rm \nu \omega}} \right]}}e^{ - i{\rm \omega} t}$$where
$${\rm \beta} = \displaystyle{{ - i{\rm \omega} e} \over {m\left[ {\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right) + i{\rm \nu \omega}} \right]}}e^{ - i{\rm \omega} t}$$The velocity has a part in phase with the electric field of the laser and another part out of phase by π/2. The former gives rise to time average power absorption by the electrons,
$$\eqalign{H & = \displaystyle{1 \over 2}\langle{{\mathop{\rm Re}\nolimits} {\overrightarrow E}_T.{\mathop{\rm Re}\nolimits} \overrightarrow v} \rangle H = \displaystyle{1 \over 2}\langle{{\mathop{\rm Re}\nolimits} \lpar { - e{\overrightarrow E}_{\rm T}} \rpar \cdot {\mathop{\rm Re}\nolimits} \overrightarrow v} \rangle \cr & = \displaystyle{{e^2{\vert {T_{\rm A}} \vert } ^2E_0^2 {\rm \nu} {\rm \omega} ^2} \over {2m\left[ {{\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right)}^2 + \lpar {{\rm \nu}^2{\rm \omega}^2} \rpar } \right]}},}$$
where < > denotes the time average. The number of nanorods per unit area is N = 1/d 2. Hence, the power absorbed per unit time per unit area in the nanorods of radius 
$r_{n_0}$ is
$$\eqalign{P_{{\rm abs}} & = \displaystyle{{N\lpar {{\rm \pi} r_{n_0}^2 ln_{{\rm nr}}} \rpar e^2{\vert {T_{\rm A}} \vert } ^2E_0^2 {\rm \nu} {\rm \omega} ^2} \over {2m\left[ {{\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right)}^2 + \lpar {{\rm \nu}^2{\rm \omega}^2} \rpar } \right]}} \cr & = \displaystyle{{N\lpar {{\rm \omega}_{{\rm nr}}^2 r_{n_0}^2 l} \rpar {\vert {T_{\rm A}} \vert } ^2E_0^2 {\rm \nu} {\rm \omega} ^2} \over {8\left[ {{\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right)}^2 + \lpar {{\rm \nu}^2{\rm \omega}^2} \rpar } \right]}}}$$Considering P in is the total incident laser power per unit area, then the resultant laser field inside, from Eq. (7), is
$$E^2 = 8{\rm \pi} P_{{\rm in}}/c\left \vert {1 + \displaystyle{{\rm \eta} \over 2} - \displaystyle{{e{\rm \beta \pi} r_{n_0}^2 l} \over c}} \right \vert ^2$$ E 0 is related to the incident power per unit area 
$P_{{\rm in}} = A_0^2 /2{\rm \mu} _0c$ and |E T| = [|TA|A0] = [2μ0cP in]1/2|T A|.
The absorption coefficient or fraction of incident laser power absorbed is
$$F \equiv \displaystyle{{P_{{\rm abs}}} \over {P_{{\rm in}}}} = \displaystyle{{{\rm \pi \omega} _{{\rm pe}}^2 \lpar {r_{n_0}^2 /d^2} \rpar l{\rm \nu} {\rm \omega} ^2} \over {2c\left[ {{\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}} \right)}^2 + \lpar {{\rm \nu}^2{\rm \omega}^2} \rpar } \right]}}\vert {T_{\rm A}} \vert ^2$$
when 
${\rm \omega} \sim {\rm \omega} _{\rm p}/\sqrt 2 $, the absorption coefficient is greatly enhanced,
$$F = \displaystyle{{4{\rm \pi \omega} _{\rm p}^2 \lpar {r_{n_0}^2 /d^2} \rpar l} \over {c{\rm \nu} {\left \vert {1 + \displaystyle{{\rm \eta} \over 2} - \displaystyle{{e{\rm \beta \pi} r_{n_0}^2 l} \over c}} \right \vert} ^2}}$$ One can observe that F increase resonantly as 
${\rm \omega} \sim {\rm \omega} _{\rm p}/\sqrt 2 $. Equation (14) has solved mathematically using the parameter: 
$r_{n_0}/d$ = 0.01, 
$r_{n_0}$ = 1 nm, ωp = 4 × 1015 rad/s, and ν/ω = 0.1. We have plotted the absorption coefficient versus laser frequency in Figure 2. The absorption coefficient increased up to 0.60 for normal incidence and it also increases with increasing the length of the nanorods. The appreciable reduction of the absorption coefficient on changing the resonant frequency about 5% but inside the nanorod the resonant absorption is insignificant.
Fig. 2. Variation of absorption coefficient with laser frequency. For typical parameters 
$r_{n_0}/d$ = 0.01, ωp = 4 × 1015, ν/ω = 0.01 at different l = 250 and 500 nm.
Nonlinear absorption with expanding nanoroads
As the electrons of nanorods get heated, the nanorods undergoes ambipolar radial expansion at the acoustic speed,
$$C_{\rm s}\, = \,\left( {\displaystyle{{T_{\rm e}} \over {m_i}}} \right)^{1/2}$$and nanorod radius evolves with time as
$$r_{{\rm nr}} = r_{n_0} + C_{\rm s}t,$$The corresponding plasma frequency falls as
$${\rm \omega} _{{\rm p}_0}^2 r_{n_0}^3 = {\rm \omega} _{\rm p}^2 r_n^3 $$The electron–ion collision frequency decreases with electron temperature as
$${\rm \nu} = {\rm \nu} _0\lpar {T_{\rm e}/T_0} \rpar ^{ - 3/2}\left( {1 + \displaystyle{{C_{\rm s}t} \over {r_{c0}}}} \right)^{ - 3},$$where at lattice temperature, ν0 is the collision frequency.
According to the energy balance equation, laser energy is absorbing by the free electrons inside a nanorod, resulting into high temperature,
$$\displaystyle{{3dT_{\rm e}} \over {2dt}} = \displaystyle{{e^2\vert {E^2} \vert {\rm \nu} {\rm \omega} ^2} \over {3m\left[ {{\left( {{\rm \omega}^2 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over 2}{\left( {1 + \displaystyle{{c_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 3}} \right)}^2 + \lpar {{\rm \nu}^2{\rm \omega}^2} \rpar } \right]}}$$For short intense pulses we have ignored the energy transfer from the electrons to the lattice.
Using t ′ = νt, 
${t}^{\prime} = (C_{\rm s}/r_{c_0})t$ and 
$d{t}^{\prime} = (C_{\rm s}/r_{c_0})dt$
$$\displaystyle{{\partial \lpar {{{{T_{\rm e}} / T}}_0} \rpar } \over {d{t}^{\prime}}} = \displaystyle{{r_{c0}} \over {c_{\rm s}}}\left[ {\displaystyle{{e^2\vert {E^2} \vert {\rm \nu}_0{\left( {\displaystyle{{T_{\rm e}} \over {T_0}}} \right)}^{{{ - 3} / 2}}} \over {{3m{\rm \omega}^2T_0{(1 + {t}^{\prime})}^3\left[ {{\left( {1 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over {2{\rm \omega}^2}}{(1 + {t}^{\prime})}^{ - 3}} \right)}^2} + {\displaystyle{{{\rm \nu}_0^2} \over {{\rm \omega}^2}}{\left( {\displaystyle{{T_{\rm e}} \over {T_0}}} \right)}^{ - 3}{(1 + {t}^{\prime})}^{ - 6}} \right]}}}} \right]$$On solving Eq. (18),we get
$$\displaystyle{{\partial \lpar {{{{T_{\rm e}} / T}}_0} \rpar } \over {\partial t}} = \displaystyle{{e^2{\vert E \vert } ^2{\rm \nu} _0{\lpar {T_e/T_0} \rpar }^{ - 3/2}} \over {3m{\rm \omega} ^2T_0{\left( {1 + \displaystyle{{c_{\rm s}t} \over {r_{c0}}}} \right)}^3\left[ {{\left( {1 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over {2{\rm \omega}^2}}{\left( {1 + \displaystyle{{c_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 3}} \right)}^2 + \displaystyle{{{\rm \nu}_0^2 {\lpar {T_{\rm e}/T_0} \rpar }^{ - 3}{\left( {1 + \displaystyle{{C_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 6}} \over {{\rm \omega}^2}}} \right]}}$$
where 
$C_{{\rm s}_0} \equiv \lpar {T_0/m_i} \rpar ^{1/2}$.
One can obtain the absorption coefficient as done in Eq. (17),
$$F \equiv \displaystyle{{P_{{\rm abs}}} \over {P_{{\rm in}}}} = \displaystyle{{4{\rm \pi \omega} _{\rm p}^2 \lpar {r_{{\rm nr}}^2 /d^2} \rpar l{\rm \nu} _0{\lpar {T_{\rm e}/T_0} \rpar }^{ - 3/2}{\left( {1 + \displaystyle{{C_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 3}} \over {c{\rm \omega} ^2\left[ {{\left( {1 - \displaystyle{{{\rm \omega}_{\rm p}^2} \over {2{\rm \omega}^2}}{\left( {1 + \displaystyle{{c_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 3}} \right)}^2 + \displaystyle{{{\rm \nu}_0^2 {\lpar {T_{\rm e}/T_0} \rpar }^{ - 3}{\left( {1 + \displaystyle{{C_{\rm s}t} \over {r_{c0}}}} \right)}^{ - 6}} \over {{\rm \omega}^2}}} \right]{\left \vert {1 - i{\rm \eta}^2\displaystyle{{k_{1z}} \over {\rm \alpha}}} \right \vert} ^2}}$$On solving Eqs. (21) and (22) for the following parameters of nanorod : ω = 2 × 1015 rad/s, ωp/ω = 3 − 5, r nr = 1 − 10 nm, r nr/d = 0.01, l = 100 nm and e 2| E|2/3mω2T 0 = 4 − 6.
In Figure 3, we have plotted T e/T 0 versus time for different parameters. For a given nanorod radius, the electron temperature rises sharply at time t = t R when the plasmon resonance is realized. The value of t R is bigger for thicker nanorods as they take longer time to expand. However, t R decreases with laser intensity as the electron temperature rises more rapidly. We have plotted in Figure 4, the absorption coefficient versus time for different thickness of nanorods. For a particular nanorod radius, the absorption coefficient increases rapidly at t = t R. If the thickness of nanorod is increased the absorption saturates at higher levels.
Fig. 3. The enhancement in temperature with time for different normalized intensities e 2|E 2|/3mω2 and normalized frequencies ωp/ω.
Fig. 4. Variation in absorption coefficient with time for different values of e 2|E 2|/3mω2 and 
$r_{c_0}/d$.
Discussion
The nanorods over a dielectric surface offer an efficiently absorbing layer for infrared laser. The absorption is large at surface plasmon resonance. High intensity picosecond laser pulses, of pulse duration greater than the electron ion collision time, lead to heating of electrons and nanorod expansion at acoustic speed. The adiabatic cooling of electrons on expansion is significant. For expanding nanorods, plasmon resonance evolves in time. In case of high electron density nanorods, the plasmon frequency is initially larger than the laser frequency. However, as the nanorods expand, the plasmon frequency falls and plasmon resonance is realized later in time. With nanorods of higher free electron density, plasmon resonance occurs later in time. The absorption peaks are sharp and size dependent. On increasing the separation between nanorods, the areal density (number of nanorods per unit area) decreases and the absorption falls.
Acknowledgement
We are thankful to Prof. V. K. Tripathi, IIT Delhi for useful discussions.
