Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-04T15:16:56.531Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear absorption of ultra short laser pulses by clusters

Published online by Cambridge University Press:  06 March 2006

M. KANAPATHIPILLAI
M. KANAPATHIPILLAI
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany and Technische Universität Darmstadt, Darmstadt, Germany
Rights & Permissions [Opens in a new window]

Abstract

Very good absorption of ultra short laser pulses by clusters is a well established fact. Efficient collisional absorption occurs only in the initial phase of the pulse. However, experiments and numerical simulations show that even after collisional absorption becomes inefficient subsequent to heating of the electrons, strong absorption continues. There have been a few attempts to model this phenomenon in terms of driven “linear” oscillator models with time dependent eigen-frequencies. Here we propose a nonlinear oscillator model and show that nonlinear resonance is the leading mechanism responsible for the collisionless absorption. Further it is demonstrated, on the basis of Lyapunov spectra, that laser-cluster interaction, under certain conditions, exhibits chaotic behavior.

Keywords

ChaosClustersLaser-cluster interactionLyapunov exponents
Type
Research Article
Information
Laser and Particle Beams , Volume 24 , Issue 1 , March 2006 , pp. 9 - 14
Copyright
© 2006 Cambridge University Press

1. INTRODUCTION

Interaction processes of intense laser and particle radiation (Deutsch, 2004) with matter is currently of high interest to the research community. This is in part due to the fact that new roads to inertial fusion (Hora, 2004) and the investigation of matter under extreme with powerful accelerators (Hoffmann et al., 2005; Tahir et al., 2005) are opened. At many places worldwide new laser installations and particle or heavy ion accelerators are being built to address this problem. Ultra short laser pulses are a new tool to transform matter into high density plasmas at the shortest time scale which is presently possible. Matter in the form of clusters is an interesting research area in itself and the interaction of intense laser pulses with clusters is not understood in full detail (Shokri et al., 2005a, 2005b). Cluster ion beams have also been proposed as beams for inertial fusion energy (Tahir et al., 1997) due to the collective stopping phenomena (Deutsch et al., 2005). In this paper we will investigate the interaction of ultra short laser pulses with clusters.

Clusters absorb ultra short laser pulses very efficiently because:

(a) Their density is comparable to that of solid matter and

(b) Having dimensions smaller than the wavelength of the irradiating laser, they are completely bathed in the latter.

While the absorption in unclustered gas medium is at most a few percent of the incident radiation, in clustered media it can be as high as 95% (Ditmire et al., 1997). The absence of heat transport via conduction coupled with the extraordinary absorption rate leads to a very hot plasma with temperatures in the range of several keV. The formation of this high temperature plasma is attested by the emission of copious quantities of X-ray photons in the keV range (McPherson et al., 1994; Fukuda et al., 2004; Magunov et al., 2003), coherent (Donnelly et al., 1996), and incoherent (McPherson et al., 1994; Ditmire et al., 1995) harmonics of the incident laser, electrons with energies ranging up to several keV (Springate et al., 2003), and multiply charged ions with energies up MeV (Ditmire et al., 1998; Zhu et al., 2003). The existence of high energy ions is further confirmed by the occurrence of fusion reactions in deuterium clusters. Up to 104 neutrons have been observed from deuterium clusters (50 Å diameter) when they were irradiated by a 120 mJ laser (wavelength 820 nm) pulse of 35 fs duration (Ditmire et al., 1999).

It is clear that collisional absorption, although very effective in clusters during the initial phase, cannot account for all of the absorption because it becomes ineffective as the temperature of the electrons increases beyond 1 keV or as the instantaneous intensity becomes large owing to the v3 dependence of the collision frequency (electron inertia neglected). Indeed particle in cell (PIC) and molecular dynamics (MD) calculations attest this experimental fact (Greschik & Kull, 2004; Bauer, 2004). However, PIC/MD simulations do not elucidate the physical mechanism of absorption.

Irreversible absorption of the laser pulse can occur if and only if the current induced by the laser pulse has the same phase as the laser for most of the time, that is, ∫j × Edt ≠ 0. The integral is carried out over the total interaction time. This is possible only if j is, in the average not orthogonal to E and the phase is equal. While not surprisingly, the necessity for phase matching has been recognized (Taguchi et al., 2004; Jungreuthmayer et al., 2004), the mechanism for phase matching has not been elucidated so far. In this paper we show that nonlinear resonance is the mechanism for phase matching and consequently for irreversible absorption. Furthermore it is shown that ultra short pulse laser interaction with the cluster can be modeled as a nonlinear giant dipole oscillator, and the behavior of such an oscillator, for certain sets of parameters can be chaotic.

2. MODEL

As mentioned in the introduction, we will describe the laser-cluster interaction in the framework of a giant dipole model. The giant dipole model regards the ions to form an immobile positively charged sphere and the electrons as a mobile negatively charged spherical cloud driven by the combined fields of the ion sphere and the laser field. This picture has emerged as a result of PIC simulations of ultra short laser pulses with cylindrical and spherical clusters (Greschik & Kull, 2004). A similar model consisting of a driven damped harmonic oscillator with a time dependent eigen-frequency has also been arrived at for interpreting results obtained from simulating laser-cluster interactions using a hierarchical tree code (Saalmann & Rost, 2003). However this model considers only linear resonance. For simplicity, we will make few further assumptions as well. First of all, we will consider the motion of the center of mass of the electron cloud only, disregarding the electron-electron interactions. The second assumption consists of ignoring the expansion of the electron sphere due to heating and distortion and further disintegration of the electron cloud due to tidal forces. Thus, the giant dipole model consists of the evolution of a single negatively charged particle having the same mass and charge as the entire electron cloud moving in the potential well of the ion sphere driven by the laser pulse. Thus the equation of motion of the system can be written as:

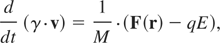
where r and v are the position vector and velocity of the center mass of the electron sphere respectively, and γ is the usual relativistic factor. The coordinate origin is located at the center of the ion sphere. F is the force between the electron and the ion sphere, M and q are the total mass and charge of the electron sphere, respectively. For the sake of simplicity, the effect of the laser magnetic field has also been neglected. A similar model which incorporates the effects of the magnetic field and expansion of the electron sphere has been described elsewhere (Kanapathipillai et al., 2004).The force F can be evaluated easily as:

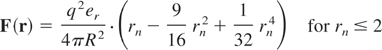
or

where rn = r/R. The potential associated with this force field is,

The arbitrary constant is hosen so as to ensure that the potential is zero at r = 0. As |r| → ∞, Φ(r) → 6/5·q2/4πR, which is the energy required to completely separate the electron and the ion spheres (complete “outer ionization”). We assume that the laser pulse has the form which is observed in experiments (Fuerbach et al., 2005) and can be described by:

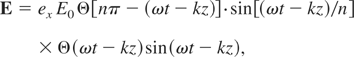
where the cluster is initially at rest. The function Θ is a step function which is either 1 or 0 depending on the argument in order to assure that the pulse is non-zero only in a small interval.

Note that for small oscillations (rn << 1) the potential is harmonic and consequently for small laser intensities (I ≤ 1018 Wm2) the behavior of the oscillator is identical to that of a harmonic one. In this case the solution can be found analytically and the expression for absorbed energy coincides with the one obtained using quantum mechanics with a first order perturbative approximation. Naturally as one would expect, the absorption of laser pulses having frequency far below the Mie resonance frequency

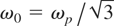
, ωp the plasma frequency associated with the electron density, is negligibly small.

As |r| increases the restoring force F weakens and the frequency of free (laser pulse absent) oscillations, decreases. Indeed for large amplitude oscillations, the potential can be effectively regarded as Coulomb, and the frequency of free oscillations in the potential well is described by Kepler's law, that is, it is proportional to rmax−3/2 (Kanapathipillai et al., 2004). In other words, with increasing amplitude, the frequency of nonlinear oscillations decrease, opening the way for an efficient coupling with the laser pulse whose frequency is far smaller than the Mie frequency. Indeed this is what is observed by solving Eq. (1) for various laser intensities. Figure 1 shows a particular solution of the Eq. (1) for ω/ω0 = 0:3 in which nonlinear resonance and therefore irreversible absorption occur. One can clearly see the phase matching between v and E during the resonance. When we consider the first resonance, at t/TL ≈ 5:0 just before the resonance, the phase between v and E is π/2 and at t/TL = 6:5, just after the resonance it is −π/2. The horizontal line depicts the outer ionization energy for an electron. In this particular case the cluster is fully outer-ionized, that is, the electron and the ion spheres completely decouple from each other.

Solution of Eq.(1) for R = 50 Å, ω/ωo = 0:3, n = 24, and the peak intensity I0 = 1/2·ε0 cE02 = 2.54 1021 Wm−2. TL-laser period; E denotes the electric field strength and β is an arbitrary factor. ea and eI are the average energy absorbed by an electron of the cluster and its outer ionization energy respectively. Nonlinear resonances occurs at about t = TL ≈ 6 and t/TL ≈10. Note the abrupt alteration of the relative phase between the laser electric field and v during the passage through the resonances and the corresponding drastic change in the absorbed energy.

Figure 2 shows the net absorption for the experimentally relevant parameter range. The figure overestimates the absorbed energy because expansion of the electron sphere due to heating has not been taken into account in our analysis. However when this expansion is taken into account, average absorption energy of some 5 keV per electron results which is in the same ball park as experimentally measured electron energies (Springate et al., 2003).

Average absorbed energy ε;π per electron in units of electron rest energy me c2 as a function of the frequency of the irradiating laser pulse and its peak intensity for a cluster with R = 50 Å. The length of the laser pulse was 12 cycles; therefore the pulse length was not constant due to the variation of the frequency of the laser pulse. Note the sensitivity of the absorbed energy on the frequency and peak intensity of the laser pulse.

3. CHAOS

The sensitive dependence of the absorbed energy on the frequency and the intensity of the laser pulse as seen in Figure 2 is striking. Since the equation of motion of the oscillator Eq. (1) constitutes an autonomous dynamical system containing three equations (time is taken as both dependent and independent variable to make the system appear autonomous), one may surmise chaos as the cause of the sensitivity. To further ascertain the nature of the evolution of the oscillator, we have also constructed a bifurcation diagram by varying the intensity of the laser pulse while keeping the frequency and the number of cycles in the laser pulse constant. Figure 3 shows such a bifurcation diagram. To confirm this result we evaluate the characteristic exponents of the dynamical system (Udwadia & von Bremen, 2002). It is obvious that when the characteristic spectra become positive, chaos is indicated by the bifurcation diagram. Finally, Figure 4 shows the characteristic spectra for experimentally relevant parameter range.

Bifurcation diagram (points) and the characteristic spectra (Lyapunov spectra-solid line) as a function of peak laser intensity I0. As before R = 50 Å, ω/ω0 = 0:3, n = 24. Note that the positively of the characteristic spectra coincides with the onset of chaos.

Characteristic spectra as a function of peak laser intensity I0 and ω/ω0. As before R = 50Å, and n = 24.

4. CONCLUSION

We have studied collisionless absorption of ultra short pulses by clusters in the frame work of a giant dipole model. It has been shown that nonlinear resonance is the main mechanism of irreversible energy exchange between the laser pulse and the cluster. Further it has been demonstrated, on the basis of characteristic spectra that the interaction of ultra short pulses with clusters is, for certain range of parameters chaotic.

ACKNOWLEDGMENT

The research was funded by the DIP (German Israel Programme)

NOTE ADDED BY THE EDITOR

Dr. Kanapathipillai died unexpectedly while the paper was in the final stage of processing. His colleagues at GSI and TU-Darmstadt (P. Mulser, T. Schlegel, and D.H.H. Hoffmann) helped with the final version of this paper. We will keep Dr. Kanapathipillai's memory alive with us, and will remember him as a dedicated scientist. His friends fondly remember him and pay their tribute to the departed soul.

References

REFERENCES

Bauer, D. (2004). Small rare gas clusters in laser fields: Ionization and absorption at long and short laser wavelengths. J. Physics B 37, 3085–3101.Google Scholar
Deutsch, C. (2004). Penetration of intense charged particle beams in the outer layers of precompressed thermonuclear fuels. Laser Part. Beams 22, 115–120.Google Scholar
Deutsch, C., Bret, A. & Fromy, P. (2005). Mitigation of electromagnetic instabilities in fast ignition scenario. Laser Part. Beams 23, 5–8.Google Scholar
Ditmire, T., Donnelly, T., Falcone, R.W. & Perry, M.D. (1995). Strong X-ray-emission from high-temperature plasmas produced by intense irradiation of clusters. Phys. Rev. Lett. 75, 3122–3125.Google Scholar
Ditmire, T., Smith, R.A., Tisch, J.W.G. & Hutchinson, M.H.R. (1997). High intensity laser absorption by gases of atomic clusters. Phys. Rev. Lett. 78, 3121–3124.Google Scholar
Ditmire, T., Springate, E., Tisch, J.W.G., Shao, Y.L., Mason, M.B., Hay, N., Marangos, J.P. & Hutchinson, M.H.R. (1998). Explosion of atomic clusters heated by high-intensity femtosecond laser pulses. Phys. Rev. A 57, 369–382.Google Scholar
Ditmire, T., Zweiback, J., Yanovsky, V.P., Cowan, T.E., Hays, G. & Wharton, K.B. (1999). Nuclear fusion from explosions of femtosecond laser-heated deuterium clusters. Nature 398, 489–492.Google Scholar
Donnelly, T.D., Ditmire, T., Neuman, K., Perry, M.D. & Falcone, R.W. (1996). High-order harmonic generation in atom clusters. Phys. Rev. Lett. 76, 2472–2475.Google Scholar
Fuerbach, A., Fernandez, A., Apolonski, A., Fuji, T. & Krausz, F. (2005). Chirped-pulse oscillators for the generation of high-energy femtosecond laser pulses. Laser Part. Beam 23, 113–116.Google Scholar
Fukuda, Y., Akahane, Y., Aoyama, M., Inoue, N., Ueda, H., Kishimoto, Y., Yamakawa, K., Faenov, A.Y., Magunov, A.I., Pikuz, T.A., Skobelev, I.Y., Abdallah, J., Csanak, G., Boldarev, A.S. & Gasilov, V.A. (2004). Generation of X rays and energetic ions from superintense laser irradiation of micron-sized Ar clusters. Laser Part. Beams 22, 215–220.Google Scholar
Greschik, F. & Kull, H. (2004). Two-dimensional PIC simulation of atomic clusters in intense laser fields. Laser Part. Beams 22, 137–145.Google Scholar
Hoffmann, D.H.H., Blazevic, A., Ni, P., Rosmej, O., Roth, M., Tahir, N.A., Tauschwitz, A., Udrea, S., Varentsov, D., Weyrich, K. & Maron, Y. (2005). Present and future perspectives for high energy density physics with intense heavy ion and laser beams. Laser Part. Beams 23, 47–53.Google Scholar
Hora, H. (2004). Developments in inertial fusion energy and beam fusion at magnetic confinement. Laser Part. Beams 22, 439–449.Google Scholar
Jungreuthmayer, C., Geissler, M., Zanghellini, J. & Brabec, T. (2004). Microscopic analysis of large-cluster explosion in intense laser fields. Phys. Rev. Lett. 92, 133401.Google Scholar
Kanapathipillai, M., Mulser, P., Hoffmann, D.H.H., Schlegel, T., Maron, Y. & Sauerbrey, R. (2004). Net charge of a conducting microsphere embedded in a thermal plasma. Phys. Plasmas 11, 3911–3914.Google Scholar
Magunov, AI., Faenov, AY., Skobelev, I.Y., Pikuz, T.A., Dobosz, S., Schmidt, M., Perdrix, M., Meynadier, P., Gobert, O., Normand, D., Stenz, C., Bagnoud, V., Blasco, F., Roche, J.R., Salin, F. & Sharkov, B.Y. (2003). X-ray spectra of fast ions generated from clusters by ultrashort laser pulses. Laser Part. Beams 21, 73–79.Google Scholar
McPherson, A., Thompson, B.D., Borisov, A.B., Boyer, K. & Rhodes, C.K. (1994). Multiphoton-induced X-ray-emission at 4–5 keV from Xe atoms with multiple core vacancies. Nature 370, 631–634.Google Scholar
Saalmann, U. & Rost, J.M. (2003). Ionization of clusters in intense laser pulses through collective electron dynamics. Phys. Rev. Lett. 91, 223401.Google Scholar
Shokri, B., Niknam, A.R. & Krainov, V. (2004a). Cluster structure effects on the interaction of an ultrashort intense laser field with large clusters. Laser Part. Beams 22, 13–18.Google Scholar
Shokri, B., Niknam, A.R. & Smirnov, M. (2004b). Ionization processes in the ultrashort, intense laser field interaction with large clusters. Laser Part. Beams 22, 45–50.Google Scholar
Springate, E., Aseyev, S.A., Zamith, S. & Vrakking, M.J.J. (2003). Electron kinetic energy measurements from laser irradiation of clusters. Phys. Rev. A 68, 053201.Google Scholar
Taguchi, T., Antonsen, T.M. & Milchberg, H.M. (2004). Resonant heating of a cluster plasma by intense laser light. Phys. Rev. Lett. 92, 205003.Google Scholar
Tahir, NA., Kain, V., Schmidt, R., Shutov, A., Lomonosov, I.V., Gryaznov, V., Piriz, A.R., Temporal, M., Hoffmann, D.H.H. & Fortov, V.E. (2005). The CERN large hadron collider as a tool to study high-energy density matter. Phys. Rev. Lett. 94, 135004.Google Scholar
Tahir, NA., Lutz, K.J., Geb, O., Maruhn, J.A., Deutsch, C. & Hoffmann, D.H.H. (1997). Inertial confinement fusion using hohlraum radiation generated by heavy-ion clusters. Phys. Plasmas 4, 796–816.Google Scholar
Udwadia, F.E. & von Bremen, H.F. (2002). Computation of Lyapunov characteristic exponents for continuous dynamical systems. Zeitschrift Fur Angewandte Mathematik Und Physik 53, 123–146.Google Scholar
Zhu, P.P., Liu, H.S. & Xu, Z.Z. (2003). Theoretical investigation of high-energy ions produced from laser-cluster interactions. Laser Part. Beams 21, 593–597.Google Scholar
Figure 0

Solution of Eq.(1) for R = 50 Å, ω/ωo = 0:3, n = 24, and the peak intensity I0 = 1/2·ε0 cE02 = 2.54 1021 Wm−2. TL-laser period; E denotes the electric field strength and β is an arbitrary factor. ea and eI are the average energy absorbed by an electron of the cluster and its outer ionization energy respectively. Nonlinear resonances occurs at about t = TL ≈ 6 and t/TL ≈10. Note the abrupt alteration of the relative phase between the laser electric field and v during the passage through the resonances and the corresponding drastic change in the absorbed energy.

Figure 1

Average absorbed energy ε;π per electron in units of electron rest energy me c2 as a function of the frequency of the irradiating laser pulse and its peak intensity for a cluster with R = 50 Å. The length of the laser pulse was 12 cycles; therefore the pulse length was not constant due to the variation of the frequency of the laser pulse. Note the sensitivity of the absorbed energy on the frequency and peak intensity of the laser pulse.

Figure 2

Bifurcation diagram (points) and the characteristic spectra (Lyapunov spectra-solid line) as a function of peak laser intensity I0. As before R = 50 Å, ω/ω0 = 0:3, n = 24. Note that the positively of the characteristic spectra coincides with the onset of chaos.

Figure 3

Characteristic spectra as a function of peak laser intensity I0 and ω/ω0. As before R = 50Å, and n = 24.