1. INTRODUCTION
Since the development of high-intensity lasers (Strickland & Mourou, Reference Tabak, Munro and Lindl1985), many schemes to accelerate high-energy and directed ion beams have been studied (Fews et al., Reference Fleischer, Price and Walker1994; Wilks et al., Reference Zepf, Clark, Beg, Clarke, Dangor, Gopal, Krushelnick, Norreys, Tatarakis, Wagner and Wei2001; Macchi et al., Reference Martinez-Val, Eliezer, Piera and Velarde2013). These beams have many interesting characteristics such as a broad spectrum, a short duration, a large number of particles per cm2, and a high-energy electron beam at the front (Fuchs et al., Reference Krainov2006). We propose to use such beams to explore nuclear physics in new physical conditions. Several studies already exist concerning the use of laser-generated proton beams to produce radioisotopes (Spencer et al., Reference Strickland and Mourou2001; Ledingham et al., Reference Lifschitz, Farengo and Arista2004). Among many other applications, such ion beams can be used to produce aneutronic fusion reactions in the context of energy production. These reactions would overcome the difficult issues of energy recuperation and nuclear activation that occur with the high-energy neutrons produced in the classical deuterium–tritium (D–T) fusion reaction.
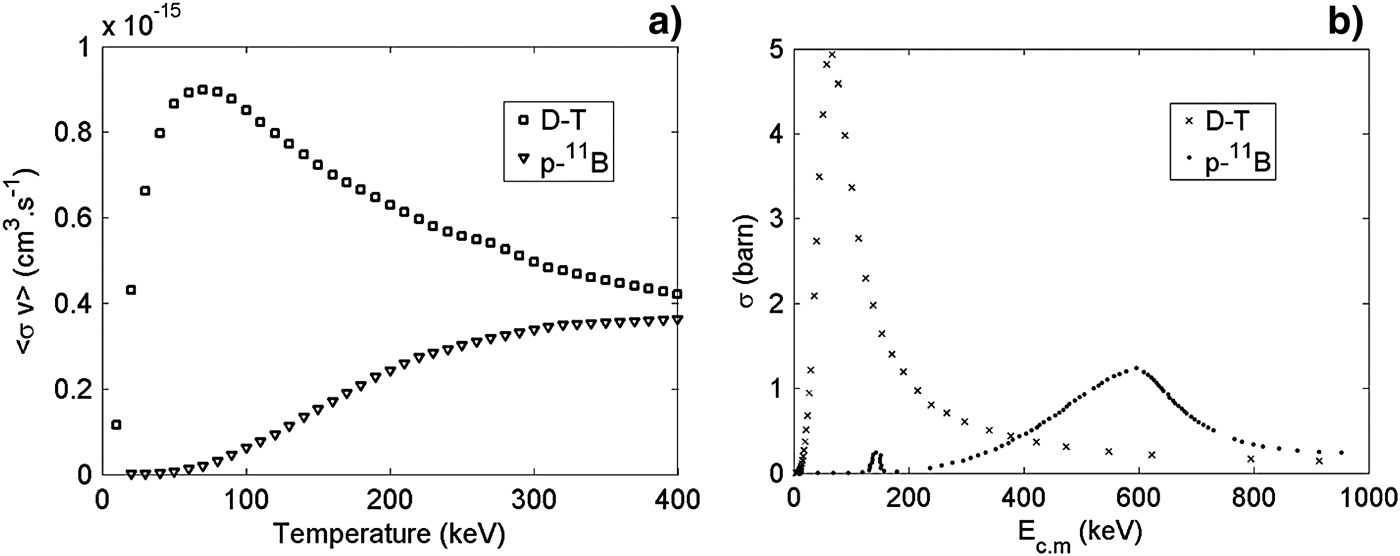
In the direct and indirect-drive schemes designed for D–T fuel ignition, a compression stage in the nanosecond regime and a very high temperature are required (Tabak et al., Reference von Seggern1990; Lindl, Reference Macchi, Borghesi and Passoni1995). As shown in Figure 1a, to reach a high fusion rate, characterized by the Maxwell-averaged reaction reactivity 〈σv〉, where σ is the cross-section of the reaction and v the relative velocity of the ions, using these schemes with a proton–boron-11 (p–11B) fuel, it is necessary to reach a temperature almost ten times higher than for the D–T fuel (Nevins & Swain, Reference Picciotto, Margarone, Velyhan, Belluti, Krasa, Szydlowsky, Bertuccio, Shi, Mangione, Prokupek, Malinowska, Krousky, Ullschmied, Laska, Kucharuk and Korn2000). This would request exorbitant laser energy with the present technologies. The idea of the scheme discussed in this paper is to produce the reactions out of thermal equilibrium regime using the directed energy of laser-accelerated protons. We therefore show in Figure 1b the direct reaction cross-sections as a function of center-of-mass energy for D–T and p–11B fusion reactions. Although the cross-section for D–T is higher, protons with energies close to the 614 keV wide resonance could induce as many or even more fusion reactions in 11B fuel than deuterons of 150 keV in a T fuel. The p–11B becomes a competitive fuel when it is used out of thermal equilibrium.

Fig. 1. (a) Maxwell-averaged reaction reactivity versus temperature and (b) total fusion cross-section versus center-of-mass energy for D–T and p–11B fusion reactions (Nevins & Swain, Reference Picciotto, Margarone, Velyhan, Belluti, Krasa, Szydlowsky, Bertuccio, Shi, Mangione, Prokupek, Malinowska, Krousky, Ullschmied, Laska, Kucharuk and Korn2000).
Many theoretical studies have addressed the production of aneutronic fusion reactions since the 1970s (Moreau, Reference Nevins and Swain1977; Martinez-Val et al., Reference McCall, Young, Ehler, Kephart and Godwin1996; Lifschitz et al., Reference Lindl2000; Lalousis et al., Reference Ledingham, McKenna, McCanny, Shimizu, Yang, Robson, Zweit, Gillies, Bailey, Chimon, Clarke, Neely, Norreys, Collier, Singhal, Wei, Mangles, Nilson, Krushelnick and Zepf2014) and recently, experimental demonstration of high numbers of reactions have been published (Belyaev et al., Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov2005; Picciotto et al., Reference Snavely, Zhang, Akli, Chen, Freeman, Gu, Hatchett, Hey, Hill, Key, Izawa, King, Kitagawa, Kodama, Langdon, Lasinski, Lei, MacKinnon, Patel, Stephens, Tampo, Tanaka, Town, Toyama, Tsutsumi, Wilks, Yabuuchi and Zheng2014). These later works are in continuity with earlier studies concerning the production of nuclear reactions by laser, exploiting the accelerated ions in the heated matter (Floux et al., Reference Fuchs, Antici, D'Humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pépin and Audebert1970; Yamanaka et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely1972; McCall et al., Reference Mora1973). The high-energy ions were directly generated in the target where the nuclear reactions were produced. The purpose of these experiments was to optimize the laser energy absorption in matter to accelerate ions at sufficient energy (≥MeV), close to the resonances of the reaction cross-section, to reach high numbers of reactions. Two main parameters can come into play. First, to produce high number of ions at the required high-energy level, one possibility is to optimize the laser intensity as proposed by Belyaev et al. (Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov2005) using a high-intensity laser (≥1018 W cm−2) focused on thick boron and hydrogen (BCH2) compound targets. Secondly, it is also possible to optimize the target structure as proposed by Picciotto et al. (Reference Snavely, Zhang, Akli, Chen, Freeman, Gu, Hatchett, Hey, Hill, Key, Izawa, King, Kitagawa, Kodama, Langdon, Lasinski, Lei, MacKinnon, Patel, Stephens, Tampo, Tanaka, Town, Toyama, Tsutsumi, Wilks, Yabuuchi and Zheng2014), using well-defined layer of boron dopants in hydrogen-enriched silicon targets. In this paper, we present a new and different way to produce aneutronic fusion reactions. Following our previous work (Labaune et al., Reference Lalousis, Hora and Moustaizis2013), our proposed scheme is based on laser-produced proton interaction with a thick boron target instead of direct photon interaction. In this paper, we present new and in-depth results from our experimental study. Then, we compare our approach to initiate p–11B fusion reactions with the Belyaev scheme.
Scheme of Principle
The well-known fusion reaction between a proton and a 11B nucleus produces three α-particles by three reaction channels described in Eqs (1)–(3), and releases ~8.7 MeV (Ajzenberg-Selove, Reference Ajzenberg-Selove1990).
The α-particle energies depend on the reaction channels and are between a few hundred keV and ~10 MeV (Becker et al., Reference Becker, Rolfs and Trautvetter1987). The predominant channels go through the formation of a compound nucleus 12C* followed by sequential α decays via an unbound 8Be in its fundamental (1) or first-excited (2) state. The direct 3α-particle mechanism (3) contributes to <5% of the total fusion cross-section (Becker et al., Reference Becker, Rolfs and Trautvetter1987). Note that a fourth channel exists with a very low cross-section, that produces a 12C* compound nucleus that decays by γ emission, releasing ~15.9 MeV. The p–11B cross-section shown in Figure 1b as a function of the center-of-mass energy, is characterized by two low-energy resonances at E c.m = 148 keV and E c.m = 614 keV (Ajzenberg-Selove, Reference Ajzenberg-Selove1990), that are very interesting for producing high numbers of reactions.
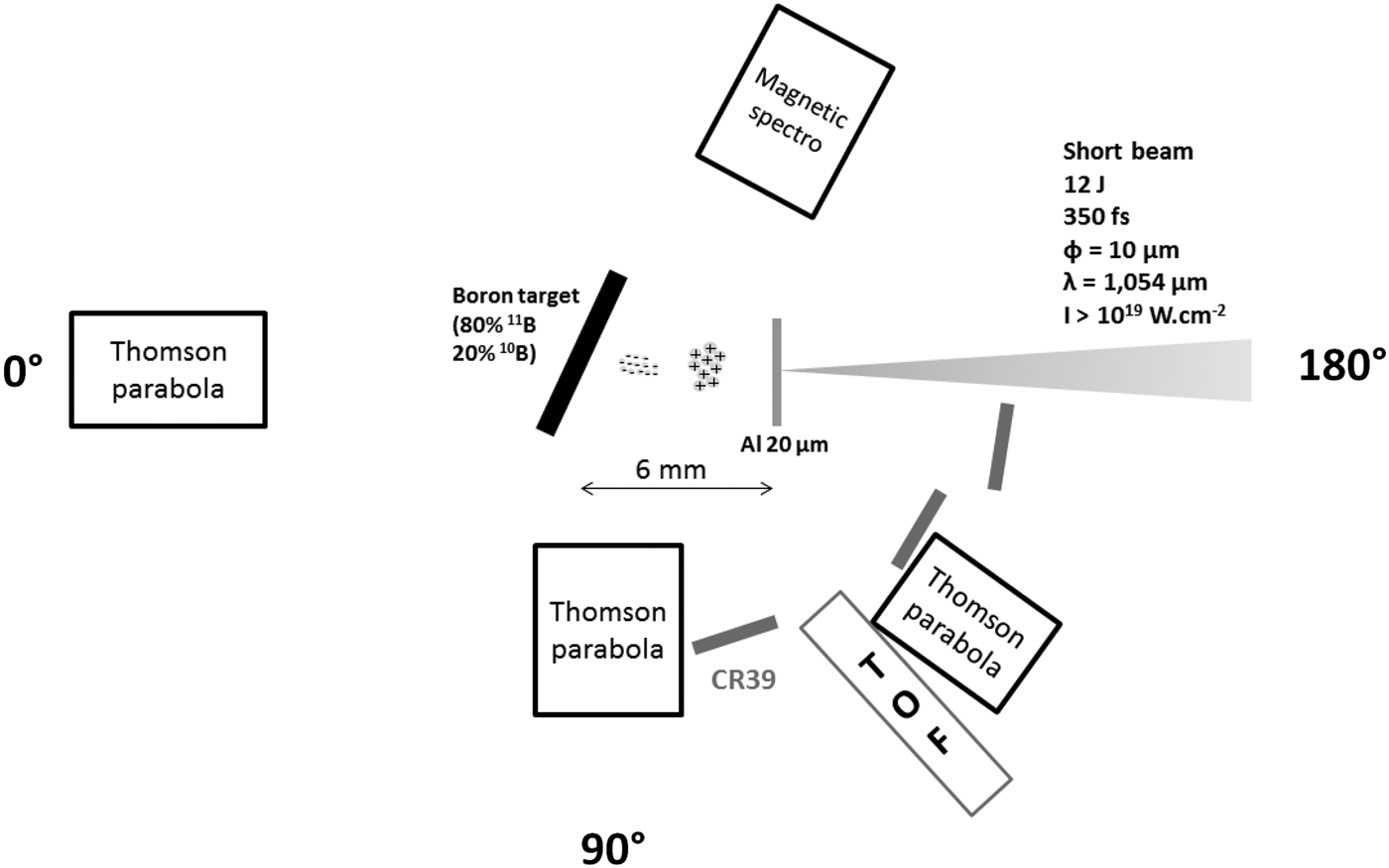
Our scheme of principle proposed to produce p–11B fusion reactions is presented in Figure 2 with the experimental setup used at the ELFIE facility (at the LULI Laboratory).

Fig. 2. Experimental setup using one laser beam and two targets. Particle diagnostics such as CR39 track-detectors, Thomson Parabola, magnetic spectrometer, and time-of-flight detectors were placed to characterize the proton beam spectrum accelerated by TNSA and to detect α-particles emitted by the boron target.
We chose to accelerate protons by the Target Normal Sheat Acceleration (TNSA) mechanism (Mora, Reference Moreau2003; Fuchs et al., Reference Krainov2006). Thereby, with quite low energy (order of a few Joules), it was possible to accelerate high-energy protons in the MeV range using laser intensities above 1018 W cm−2. For that, a short laser beam (12 J, 350 fs, λ = 1.056 µm) was focused at normal incidence on a thin aluminum foil (with initial thickness of 20 µm) by an off-axis parabola (f = 300 mm), producing laser intensities of 1019 W cm−2. The TNSA ion beams were mainly dominated by protons that were directed toward a boron target tilted by an angle of 45° and compound by 80% of 11B and 20% of 10B, to initiate nuclear reactions. The two targets were separated by 6 mm.
The points of interest of this scheme are the following. First, we do not use a costly proton heating stage because all the energy necessary for fusion is transferred by the acceleration mechanism and is contained in the particle motion. Secondly, the laser-generated particle beams differ from classical particle accelerator beams: they have a large spectrum, a high-intensity and there is an electron beam at the front that may alter the physical conditions of the proton interaction with the boron target. Indeed, the number of particles colliding with the target per second for TNSA beams is expected to be several orders of magnitude higher than for high-intensity accelerator proton beams. For all these reasons, we can explore new conditions to study nuclear physics.
Our experiment was designed to have the possibility to vary laser energy and target geometric parameters (the distance between the primary aluminum foil target and the second boron target, tilt angles, etc.) to find an optimum configuration to reach the highest number of reactions. We also aimed at reproducing Belyaev experiment. For this purpose, we directly focused the short laser pulse on a similar target compound by BCH2.
To study our scheme efficiency, we had to determine the number of produced reactions by counting the number of α-particles emitted by the boron target. An important effort was dedicated to the discrimination of the α-particles from all the other energetic particles (protons, carbon ions, etc.). That is why we used a complete set of particle diagnostics: CR39 track-detectors, Thomson Parabola, a magnetic spectrometer, time-of-flight detectors, and active nuclear diagnostics. This setup enabled us to differentiate the ions according to their mass and their ionizing state and to determine their energies.
CR39 track-detectors are plastic polymers sensitive to ion collisions (Fleischer et al., Reference Floux, Cognard, Denoeud, Piar, Parisot, Bobin, Delobeau and Fauquignon1965). After etching in a caustic solution (6 N NaOH solution at 70°C), the tracks created by the ions in the polymeric structure can be revealed and then observed with a microscope. Ion species identification comes from the track diameters. The size of the tracks depends on the nature and the energy of the ions. Heavy ions produce bigger impacts than protons and their dependence on energy varies according to their species. Moreover, the characterization of the ions was improved by using aluminum foils of various thicknesses that discriminated the ion energy. We have achieved complete calibration for our conditions (Baccou et al., 2014 CR-39 track detector calibration for H, He and C ions for laser-induced nuclear fusion product identification. Private Communication.).
In addition, we used a magnetic spectrometer that determined the energy spectra of the particles. A 0.4 T magnetic field applied along 10 cm allowed to deflect ions according to their energy, charge, and mass along the vertical axis z. A CR39 was placed at the end of the magnets. Thereby, for a signal obtained at a given value z, we could determine the energy for well-defined ion species and measure the track diameter. Coupling both information and using aluminum filter on the CR39 to suppress heavy ions, we could conclude on protons or α nature.
The Thomson Parabola diagnostic was based on the use of successive magnetic field (0.6 T applied along 50 mm) and electric field (7.7.105 V m−1 applied along 40 mm). This diagnostic thus deflected ions both in vertical and transverse directions according to their q over m ratio (where q is the charge state and m is the mass of the ions) and their energy, and ensured a clear separation between the ions species. A large imaging plate (IP) of TR type (von Seggern, Reference Yamanaka, Yamanaka, Sasaki, Yoshida and Waki1992) was placed downstream to the magnetic and electric fields to record the ion tracks (Bonnet et al., Reference Fews, Norreys, Beg, Bell, Dangor, Danson, Lee and Rose2013). Periodically during the experiment, the Thomson Parabola placed at 0° (see Figure 2), was used to characterize the accelerated proton beams. For this dedicated purpose, we did not use a boron target behind the aluminum foil. The Thomson Parabola placed at 90° was used to detect α-particles produced in the fusion reactions. Note that this detector also enabled us to control other signal variation during the shots, such as protons. The role of active nuclear diagnostics and time-of-flight detectors will not be further discussed here.
2. RESULTS
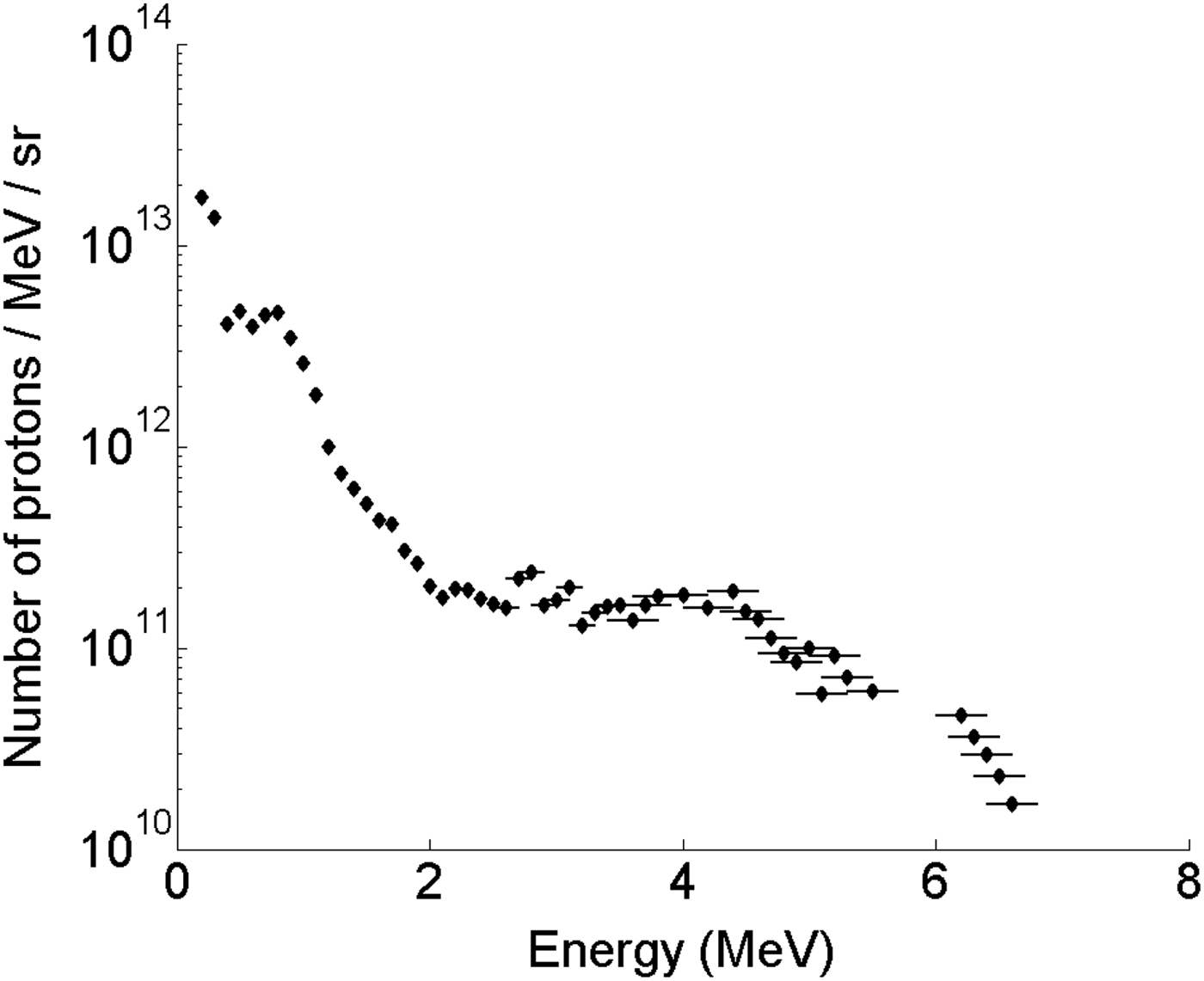
In Figure 3, we have shown a typical energy spectrum from protons accelerated by TNSA from the aluminum target. It is deduced from the signal obtained in the Thomson Parabola placed at 0° from the proton beam axis. The energy cut-off is ~6.6 ± 0.2 MeV. This value is in good agreement with previous studies (Fuchs et al., Reference Krainov2006). The total number of protons sent on the boron target was of the order of 1012. This information is fundamental to analyze the results presented below, for which a good control of the proton beam characteristics is required.

Fig. 3. Typical proton beam spectrum accelerated by TNSA at the rear face of a 20 µm aluminum foil that was used to induce nuclear reactions in the second target.
We performed a series of shots to compare the two schemes presented above: Proton–boron interaction (our scheme) with photon–BCH2 interaction (scheme proposed by Belyaev). We mainly looked at the number of α-particles detected from the CR39 track-detectors and from the magnetic spectrometer (both reported in Fig. 2).
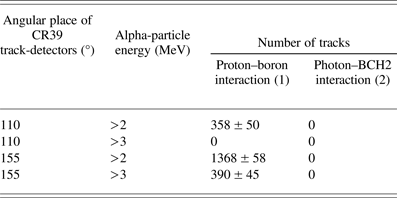
Table 1 presents the typical number of α-particles collected in CR39 track-detectors, for an arbitrary area (295 × 220 µm2) and two different directions from the proton beam axis: 110° and 155°, in the equatorial plane as observed for the two schemes. The measurements were obtained with two filters, 6 and 10 µm aluminum foils, which respectively selected α-particles above 2 and 3 MeV. No α-particles were detected when the short laser beam interacted directly with the compound target BCH2. On the opposite, in our two target scheme, we detected the presence of many α-particles. The quantitative measurements are given in Table 1 and were counted among tens of sample areas. First, we observe that the angular distribution of α-particles emerging from the thick boron target is not isotropic since the number is significantly different by a factor ~4 for the directions 110° and 155°. Moreover, the energy spectrum also depends on the angle of detection since α-particles above 3 MeV are present at 155° and not at 110°.
Table 1. Number of tracks measured on CR39 track-detectors for an arbitrary surface of 590 × 442 µm2, corresponding with α-particles

Measurements were realized for two different directions 110° and 155° from the proton beam axis and for two α energy thresholds: 2 and 3 MeV. We compare the results obtained in two schemes: (1) A proton beam accelerated by laser-initiating reactions in a boron target, (2) a laser beam initiating reactions in a BCH2 target.
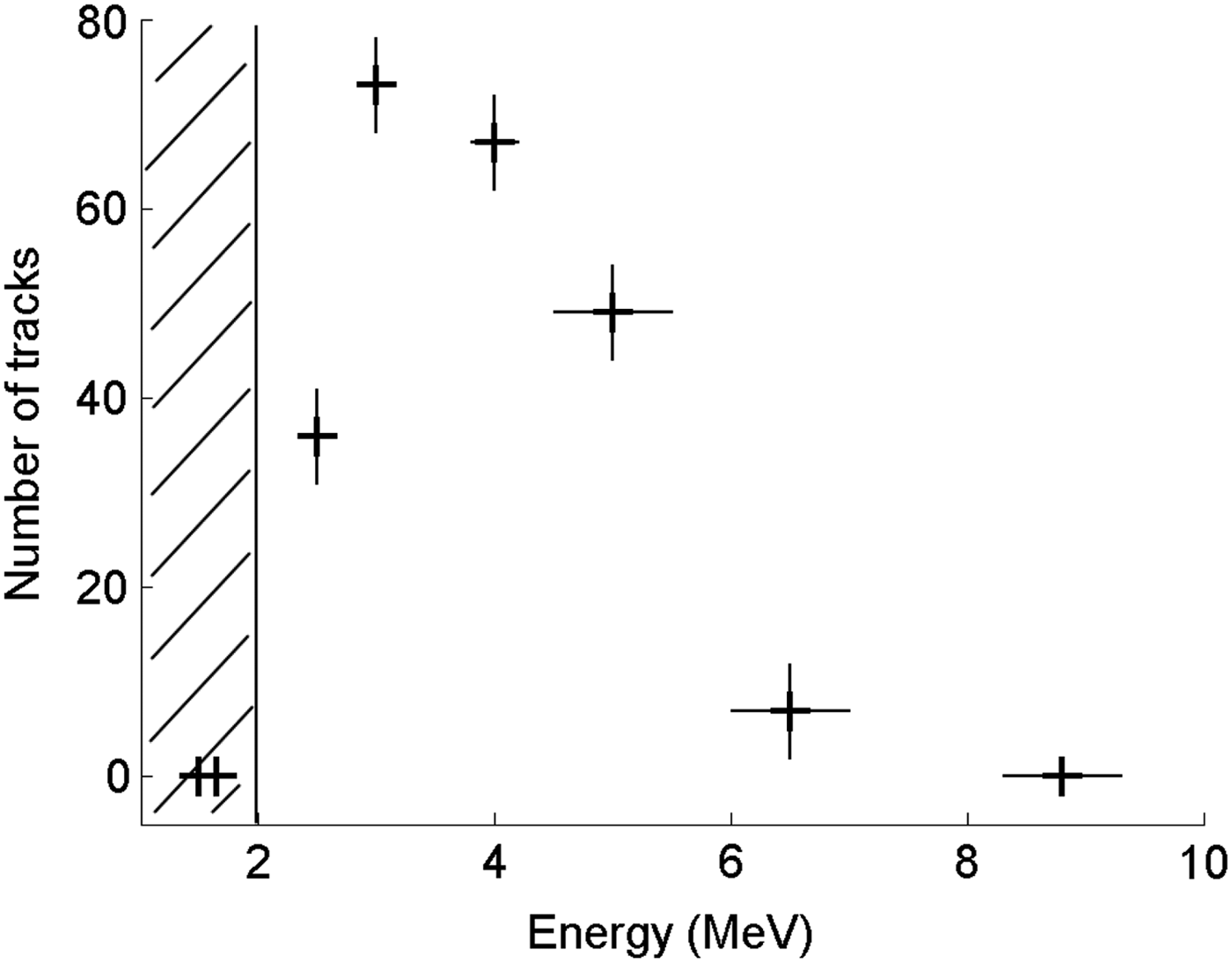
For the proton–boron interaction scheme, a more detailed study of the α-particle energy spectrum is given in Figure 4 for a detection angle of 135°. This spectrum is deduced from the number of tracks measured in the magnetic spectrometer. The particles with energy below 2 MeV could not be detected because the CR39 was covered by a 6 µm aluminum foil. The significant intensity peak between 3 and 4 MeV is in good agreement with the CR39 results.

Fig. 4. Energy spectrum of the α-particles produced by the p–11B fusion reactions initiated in a solid boron target by a laser-accelerated proton beam. Measurements were realized using the magnetic spectrometer placed at 135° from the picosecond beam axis. Counts are given for a sample area of 295 × 220 µm2.
3. DISCUSSION
From our results, it seems that it is more efficient to initiate reactions by a laser-accelerated proton beam as compared with a heating mechanism in the sub-picosecond regime, since no α-particles were detected in the direct photon–BCH2 interaction scheme. As the number of reactions produced is below the threshold number for detection, the difference of the yields could be higher than 102. One explanation could be that α energies were below the detection energy threshold of the CR39 covered by the 6 µm aluminum foil, that is, 2 MeV. However, according to the existing nuclear physics studies, many α-particles should be produced with energy values well above 2 MeV (Becker et al., Reference Becker, Rolfs and Trautvetter1987), as we found in the energy spectrum shown in Figure. 4 obtained for the proton–boron scheme. Besides, the α-particle stopping range in matter is negligible considering that they are produced in the overdense part of the plasma that has only a depth of ~0.1 µm (Belyaev et al., Reference Belyaev, Vinogradov, Matafonov, Rybakov, Krainov, Lisitsa, Andrianov, Ignatiev, Bushuev, Gromov, Rusetsky and &Dravin2005).
We now discuss the characteristics of the two schemes and we give some possible reasons that could explain why they give different results. First, we can assume that angular distributions of α-particles are not the same for the two schemes and the comparison of the yields in the same directions may not be the right method. By the way, the results obtained at 110° and 155° clearly exhibit the non-isotropic emission of fusion products in the case of proton–boron interaction. In this scheme, the proton propagation is directed into the target and the high-energy proton beam component enters relatively deep inside the target. The angular dependence could be different for the photon–BCH2 interaction case since the proton propagation direction is different and reactions do not occur deep inside the target. Hence, for future experiments, it could be interesting to increase the number of observed directions for both schemes.
Secondly, it is important to understand the role of the laser pulse profiles. Note that some parameters of ELFIE facility are different than those of the Neodynium facility in the Belyaev experiment. At ELFIE facility, the laser intensity was higher by a factor 10 and the laser pulse duration was shorter by a factor ~4. The higher intensity should be favorable to increase the yield of nuclear fusion reactions. On the other hand, the decrease of the laser pulse duration is disadvantageous (Belyaev et al., Reference Bonnet, Comet, Denis-Petit, Gobet, Hannachi, Tarisien, Versteegen and Aleonard2009). At ELFIE facility, a prepulse was present 60 ps before the main pulse with a relative intensity equal to 10−3 (three prepulses were present for the Belyaev experiment) and that also could be unfavorable to the production of reactions (Belyaev et al., Reference Bonnet, Comet, Denis-Petit, Gobet, Hannachi, Tarisien, Versteegen and Aleonard2009). Hence, the short pulse used at ELFIE facility may not have been completely optimal in some aspects with regard to the production of a high number of reactions in a photon–BCH2 interaction scheme but was quite equivalent on other fronts, with the Neodynium facility short pulse.
Finally, the physical parameters that could influence the number of reactions produced are: the boron ion density, the proton density, the cross-section of the reaction, the interaction volume, and the interaction duration. A theoretical study on these parameters for the Belyaev scheme has already been published (Krainov, Reference Labaune, Baccou, Depierreux, Goyon, Loisel, Yahia and Rafelski2005). First, it is important to keep in mind that in one case we used a boron target and in the other, we used a compound BCH2 target. In the second case, the boron density was lower by a factor 2. We believe that this cannot explain the differences on the α-particle yield of the order or larger than 102. That is why, in the first step, we can assume that the difference concerns essentially the initial number of protons of appropriate energy available to induce the fusion reactions. Always assuming that in the Belyaev scheme, reactions occur along the depth of the order of ~μm and in an area close to the laser spot diameter (15 µm), the number of protons that can produce a reaction is only about 1011 (Belyaev et al., Reference Bonnet, Comet, Denis-Petit, Gobet, Hannachi, Tarisien, Versteegen and Aleonard2009). Moreover, we can presume that an important proton fraction is rapidly ejected out of the target. In the case where the proton beam interacts with the boron target, the number of high-energy protons is about 1012 in our experiment and could be increased. We note that most protons reaching the boron target have energies corresponding to values of the cross-section above 100 mb, that is, implying rather high reaction probabilities in the target. Finally, the beam is completely directed toward the boron target, so energy is not wasted in wide space but concentrated in the zone of interest.
The question about effective fusion cross-section is in both schemes of great interest. Reactions do not occur in a solid and cold target, as usually studied in nuclear physics. On the one hand, the BCH2 target is heated by laser [T eh ~ 100 keV, T i ~ 33 keV (Krainov, Reference Labaune, Baccou, Depierreux, Goyon, Loisel, Yahia and Rafelski2005)] and on the other hand, the boron target is isochorically heated by the electron and proton beams (Snavely et al., Reference Spencer, Ledingham, Singhal, McCanny, McKenna, Clark, Krushelnick, Zepf, Beg, Tatarakis, Dangor, Norreys, Clarke, Allott and Ross2007). In the latter case, the temperature can reach tens of eV and the density is close to the solid one and this alters the stopping power of particles. Furthermore, in laser-produced plasmas or in warm dense matter, boron atoms are ionized and that could modify the cross-section of the p–11B fusion reaction. Detailed studies dedicated on this issue are needed.
The discussion on interaction volume and duration in time is more complicated. These parameters are well defined in the case where photons interact with matter because they are directly linked with the laser pulse duration and the laser spot diameter. In the case where protons interact with the boron target, interaction volume depends on which proton energy range is considered since the beam divergence depends on proton energy (Zepf et al., 2003). Considering the quite large distance of 6 mm between the two targets, interaction duration also depends on the energy range considered because all protons do not arrive at the same time.
In conclusion, we have demonstrated the possibility to initiate aneutronic fusion reactions with high yield using laser-accelerated proton beams interacting with a boron target. We have observed a significantly increased fusion rate compared with the approach where photons interact directly with a BCH2 target. Future work will address the optimization of the number of fusion reactions produced by controlling the key parameters that influence the reaction process.