Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-06T17:37:29.608Z Has data issue: false hasContentIssue false
  • English
  • Français

A new measurement of stimulated Brillouin scattering phase conjugation fidelity for high pump energies

Published online by Cambridge University Press:  22 April 2009

Y.L. Wang ,
Z.W. Lu ,
W.M. He ,
Z.X. Zheng  and
Y.H. Zhao
Y.L. Wang
Affiliation:
Institute of Opto-electronics, Harbin Institute of Technology, Harbin 150080, China
Z.W. Lu*
Affiliation:
Institute of Opto-electronics, Harbin Institute of Technology, Harbin 150080, China
W.M. He
Affiliation:
Institute of Opto-electronics, Harbin Institute of Technology, Harbin 150080, China
Z.X. Zheng
Affiliation:
Institute of Opto-electronics, Harbin Institute of Technology, Harbin 150080, China
Y.H. Zhao
Affiliation:
Institute of Opto-electronics, Harbin Institute of Technology, Harbin 150080, China
*
Address correspondence and reprint requests to: Zhiwei Lu, Institute of Opto-Electronics, Harbin Institute of Technology, P. O. Box 3031. Harbin 150080, China. E-mail: zw_lu@sohu.com
Rights & Permissions [Opens in a new window]

Abstract

In order to measure the phase conjugation-fidelity of stimulated Brillouin scattering with high pump energy more accurately and conveniently, a new measurement is proposed. According to the definition of the fidelity with optical field correlated integral, the method of recording the far-field by array camera is analyzed theoretically. By the method, an experiment for high energy stimulated Brillouin scattering is arranged, and the maximum energy of 3.42 J is achieved in a single-cell stimulated Brillouin scattering generator. For small pump pulse, the fidelity maintains a high value of more than 0.9. However, the reflectivity fluctuation is significant when the pump energy is larger than 1.5 J. As a result, the fidelity decreases gradually to 0.5 at the pump energy of 3.42 J. The reflectivity shows the same character of great fluctuation as the fidelity at high pump energy.

Keywords

Beam combinationPhase conjugationStimulated Brillouin scattering
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 2 , June 2009 , pp. 297 - 302
Copyright
Copyright © Cambridge University Press 2009

1. INTRODUCTION

Stimulated Brillouin scattering (SBS) is a convenient tool for improving the performances of high power and high energy laser systems by its phase conjugation (Lontano et al., Reference Lontano, Passoni, Riconda, Tikhonchuk and Weber2006; Kong et al., Reference Kong, Yoon, Shin, Beak and Lee2006, Reference Kong, Yoon, Beak, Shin, Lee and Lee2007; Hasi et al., Reference Hasi, Lu, Li and He2007; Kappe et al., Reference Kappe, Strasser and Ostermeyer2007; Meister et al., Reference Meister, Riesbeck and Eichler2007; Wang et al., Reference Wang, Lu, Lin, Ding and Jiang2007; Yoshida et al., Reference Yoshida, Fujita, Nakatsuka, Ueda and Fujinoki2007; Ostermeyer et al., Reference Ostermeyer, Kong, Kovalev, Harrison, Fotiadi, Megret, Kalal, Slezak, Yoon, Shin, Beak, Lee, Lu, Wang, Lin, Knight, Kotova, Straber, Scheikhobeid, Riesbeck, Meister, Eichler, Wang, He, Yoshida, Fujita, Nakatsuka, Hatae, Park, Lim, Omatsu, Nawata, Shiba, Antipov, Kuznetsov and Zakharov2008). The phase conjugation fidelity is one of the most important parameters that characterize the performance of a SBS phase conjugation mirror (PCM) (Vlad et al., Reference Vlad, Eichler, Babin, Mocofanescu, Riesbeck and Riesse2004). However, it is difficult to measure the phase conjugation fidelity via a practical experiment, for it is not easy to describe the distribution of the optical complex amplitude (Andreyev et al., Reference Andreyev, Khazanov, Palashov and Pasmanik1994). A previously reported method (also known as the energy-in-the-bucket technique) of monitoring the SBS far field phase conjugation fidelity was used, in which the transmission of the Stokes return through a pinhole located at the focus of a lens was measured for each laser shot (Dane et al., Reference Dane, Neuman and Hackel1992). The size of this aperture was chosen as the 1/e 2 diameter of the focused input beam, resulting in a transmission of approximately 86%. By monitoring the pinhole transmission of the output of the SBS cell, an indication of the correction of its wavefront to the incident beam could be obtained. As phase conjugation fidelity relates to the SBS beam's far-field divergence angular directivity, this method is of considerable practical importance (Schelonka & Clayton, Reference Schelonka and Clayton1988). However, the fidelity measured by this method will be influenced by the lens directly, especially for high pump energy. Because the measurement of the phase conjugation fidelity for the high pump energy is quite different with low pump energy. The difficulties are: (1) Air breakdown caused by high intensity laser at the focus will lead to plasma closure in pinhole, which will decrease the optical transmission, thereby reducing the measured result of fidelity. (2) It is difficult to place the pinhole on the location of the waist completely symmetrically, and the error of the location affects the measuring precision for each experiment. (3) Laser beam excursion and the changing of phase aberration caused by thermal load of amplifiers impact the focus spot on pointing to the pinhole, which is tiny for the large size of beam in the high energy laser system. We introduced an array camera method, which is convincible to measure the phase conjugation fidelity for high pump energy lasers. There is no usage of a pinhole in the measuring process and thus the result is not influenced by there difficulties. So a much better result was obtained in the case of a high intensity laser, which conquered the disadvantages of the pinhole method.

2. OPERATION PRINCIPLES

The optical path of the array camera is shown in Figure 1. The array camera consists of a long-focus lens and two pairs of mirrors, each of which contains a half-transmitting mirror and a high reflective mirror. A laser beam passes though the lens and is injected into the first pair of mirrors where there is a tiny air wedge between the two mirrors. The laser beam is reflected by the half-transmitting mirror and the high reflective mirror for many times in the air wedge. So the output laser beams from the first air wedge consist of a series of sub-beams in the vertical dimension and the intensity is decreased gradually. Because of a long depth of focus for a long focus lens, the optical path difference between any two sub-beams can be ignored. These sub-beams are injected into the second air wedges and each sub-beam is split into many sub-beams too in the horizontal dimension. These sub-beams arrange an order according to the spatial and the intensity dimensions and form array images, which cover a real state of the far-field distribution of the incident laser beam. The array images can be collected by a charge-coupled device. The array images are introduced into the calculation procedure and the focus spot is reconstructed.

Fig. 1. Schematic of the array camera for measuring far-field distribution (a) and focal spot array acquired by CCD (b).

To measure the quality of the SBS phase conjugation, the conjugation fidelity F is introduced and defined as a normalized correlation function (Lehmberg, Reference Lehmberg1982)

(1)
F={{\left \vert {\vint_0^{\rm \infty} {E_L \lpar r\rpar E_S \lpar r\rpar rdr} } \right\vert ^2 } \over {\vint_0^{\rm \infty} {\left \vert {E_L \lpar r\rpar } \right \vert ^2 rdr \vint_0^{\rm \infty} {\left\vert {E_S \lpar r\rpar } \right\vert ^2 rdr} } }}\comma \;

where E L(r) and E S(r) are amplitudes for the pump and Stokes wave fields, respectively. The numerator is an overlap integral that provides the degree of correlation of the two fields. It is maximized when E S is proportional to E L*, i.e., at wavefront reversal and matching amplitude distribution. The denominator provides a normalization to the average powers of the two fields, such that F has a maximum value of unity when E L and E S are perfect phase conjugates, and it is zero when they are uncorrelated. It is well understood and can be measured. However, it is difficult to measure the correlation integral of amplitudes of the electric field experimentally. Suni and Falk (Reference Suni and Falk1987) used a phase grating to separate the pump beam and the Stokes beam and achieved the SBS conjugate fidelity, but the phase grating is confined to high power lasers because of the restriction of aperture and the damage.

The array camera detects a far-field beam angular distribution, i.e., a far-field waist angular distribution. Therefore, the integral in Eq. (1) can be located in the vicinity of waist where the wavefront is a plane for an ideal Gaussian beam. The phases of the electric fields can be ignored in this assumption.

Since the measurement by the array camera is associated with the angular distribution of the waist of focal area, it is reasonable to set the integral region of Eq. (1) to the location of the focal plane. As an ideal Gaussian beam is considered, the phases of the electric fields in Eq. (1) can be ignored because the wavefront of the waist is equal to a plane. If the wavefront is distorted, there will be two distortions to distinguish the aberrations: local distortion and total distortion. The total phase distortion produced by thermally-induced refractive changes, when a laser beam passes through an active laser amplifier is significant in the high energy and high power laser system. The phase of the total distortion changes slowly in general, so the phases of the electric fields in Eq. (1) can be neglected in the same way. Replacing the pump and Stokes wave electric fields E L(r) and E S(r) by the energy densities w L(r) and w S(r), respectively, means the fidelity can be written as

(2)
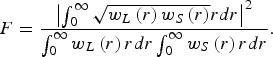
F={{\left\vert {\vint_0^{\rm \infty} {\sqrt {w_L \left(r \right)w_S \left(r \right)} rdr} } \right\vert ^2 } \over {\vint_0^{\rm \infty} {w_L \left(r \right)rdr\vint_0^{\rm \infty} {w_S \left(r \right)rdr}}}}.

According to Figure 2, the relation of $r=l \times \tan {{\rm \theta} /2}$ is clear. Introducing this expression into Eq. (2) and denoting

(3)
u_L\lpar {\rm \theta}\rpar = w_L \lpar r\rpar \tan\lpar {\rm \theta} /2\rpar \hbox{s}^2\lpar {\rm \theta} /2\rpar \comma \;
(4)
u_s\lpar {\rm \theta}\rpar = w_s \lpar r\rpar \tan\lpar {\rm \theta} /2\rpar \hbox{s}^2\lpar {\rm \theta} /2\rpar \comma \;

the fidelity can be evaluated by

(5)
F={{\left\vert {\vint_0^{\rm \pi} {\sqrt {u_L \left({\rm \theta} \right)u_S \left({\rm \theta} \right)} d{\rm \theta}} } \right\vert ^2 } \over {\vint_0^{\rm \pi} {u_L \left({\rm \theta} \right)d {\rm \theta} \vint_0^{\rm \pi} {u_S \left({\rm \theta} \right)d{\rm \theta}}}}}.

Fig. 2. The far-field distribution of Gaussian beam.

According to the definition of the energy density, the total energy of the pumping laser can be written as the integration over w L(r).

(6)
W_L=2{\rm \pi} \vint_0^{\rm \infty} {w_L \lpar r\rpar rdr}={\rm \pi} \vint_0^{\rm \pi} {u_L \lpar {\rm \theta} \rpar d {\rm \theta} }.

In this equation, the expression πu L(θ) can be seen as the energy per unit angle. Considering the principle of the array camera, the measuring result indicates the energy ratio ηL of the energy in the divergence angle θ to the total energy, the expression of πu L(θ) also can be written as $W_L {{d{\rm \eta}_L} /{d{\rm \theta}}}$. Thus, the parameter of u L(θ) is given by

(7)
u_L \lpar {\rm \theta} \rpar ={{W_L } \over {\rm \pi}}{{d{\rm \eta}_L } \over {d{\rm \theta}}}.

In the same way, the parameter of u S(θ) is given by

(8)
u_S \lpar {\rm \theta} \rpar ={{W_S } \over {\rm \pi}}{{d{\rm \eta}_S } \over {d{\rm \theta}}}.

Introducing Eqs (7) and (8) into Eq. (5), the fidelity is given by

(9)
F=\left\vert {\vint_0^{\rm \pi} {\sqrt {{{d{\rm \eta}_L } \over {d{\rm \theta}}}{{d{\rm \eta}_S } \over {d{\rm \theta} }}} d{\rm \theta}} } \right\vert ^2\comma \;

where the values of ${{d{\rm \eta}_L} / {d{\rm \theta}}}$ and ${{d{\rm \eta}_S } /{d{\rm \theta}}}$ are achieved by the far-field energy angular distribution of pump and SBS laser beams, respectively. The dependence of the energy ratio of the pump energy or the SBS energy under different far-field angle to the total energy by the array camera is shown in the Figure 3. Introducing the values of ${{d{\rm \eta}_L} / {d{\rm \theta}}}$ and ${{d{\rm \eta}_S} /{d{\rm \theta}}}$ into Eq. (9), the value of the SBS fidelity is achieved easily.

Fig. 3. The dependence of energy ratio of the pump energy or the SBS energy in different far-field angle to the total energy by the array camera.

The conjugate fidelity by this technique contains all the information of the energy angular divergence about the pump beam and the SBS beam. It is more authentic than the method of the energy-in-the-bucket technique that is influenced severely by a different selection of the pinhole in the focal plane.

3. EXPERIMENTAL RESULTS AND DISCUSSION

The primary laser source is a Nd:YLF single frequency TEM00 Q-switched laser system with a 20-ns full width at half maximum quasi-Gaussian pulse shape. This output is amplified to several tens of joules by the Nd:phosphate glass amplifier system. The experimental setup for high-energy SBS phase conjugation fidelities investigation is shown in Figure 4. An uncoated fused-silica wedge was used to sample the energy of the incoming and outgoing pulses using two calibrated energy meters. A sample of the pump beam reflected by the wedge to array camera 1 and the array spots are collected by array camera 1. The collected data are processed by a computer and the far-field angular distribution of the pump beam is thus achieved. Similarly, the far-field angular distribution of the SBS beam is also achieved by the processed data collected by array camera 2. Introducing the two distributions into Eq. (9), the phase conjugation fidelity by experiment is obtained. In this experiment, the maximum pump energy is 3.42 J, which is much higher than the SBS threshold. The nonlinear medium is selected as FC-72, which is a suitable SBS medium for very high input energy (Yoshida et al., Reference Yoshida, Kmetik, Fujita, Nakatsuka, Yamanaka and Yoshida1997).

Fig. 4. Experimental layout used to measure the SBS phase conjugation fidelity by the “array camera” technique.

For each experimental point, the calculated reflectivity was the ratio of energy measured on energy meter 2 to that on energy meter 1 (Fig. 4). The measured reflectivity is shown in Figure 5.

Fig. 5. Energy reflectivity as a function of high pump energy.

The single-cell SBS geometry is the simplest for the application in a laser system. It is necessary to enhance the energy-load of a single-cell to a higher level. However, the laser-pulse energy was limited to less than 1 J due to competition with other nonlinear processes such as stimulated Raman scattering, self-focusing, and optical breakdown resulting from high optical irradiance at the focus of the SBS cell (Dane et al., Reference Dane, Neuman and Hackel1994). To avoid the onset of detrimental nonlinearities, scaling to larger aperture geometries becomes necessary (Crofts & Damzen, Reference Crofts and Damzen1991). The energy reflectivity versus high energy and intensity is shown in Figure 5. The results show that the reflectivity increases rapidly when the energy of the incident light pulse is not more than 1 J. When the energy is more than 1.5 J, the saturation is obvious. Moreover, there is a fluctuation for higher pumping energy. The reason for these results is related to the progress of SBS. A laser beam is incident into a SBS cell where it interacts with nonlinear liquid media which corresponds to the scattering of light, called Stokes seed pulse, from thermally-induced acoustical waves present in the media. With intense coherent laser light, the rate of scattering can become so great that the acoustic wave amplitudes increase, and the Stokes pulse grows exponentially (Brignon & Huignard, Reference Brignon and Huignard2003). When the intensity of the Stokes pulse increases up to the pump pulse, the reflectivity equals approximately 100%. This is saturating and the intensity of the Stokes pulse does not increase anymore. In practice, it is difficult for the reflectivity to reach uniformity due to competition with other nonlinear processes such as Raman scattering, self-focusing, and optical breakdown resulting from the high pump energies in the oscillator. These nonlinear processes drain the pump energy and result in the fluctuation of the reflectivity. Figure 6 shows the results of the SBS phase conjugations, fidelity versus high input energy measurements, which were found using the methods explained above.

Fig. 6. Phase conjugation fidelity as a function of pump energy.

These results are consistent with those reported by Ottusch and Rockwell (Reference Ottusch and Rockwell1991) for lower pump energy. The average fidelity decreases as the pump energy increases beyond the threshold, and the fidelity becomes increasingly unstable as the reflectivity becomes more saturated, which is the same situation as in the case of reflection. At lower pump energy, the phase fidelity increases depending on the incident light and keeps a high value of more than 0.9. The fidelity decreases when the pump energy is larger than 1 J, and the value reduces from 0.9 to 0.5. In steady state, the fidelity instability results from the intense optical breakdown in the saturated reflectivity regime for high input energy that exceeds the SBS threshold greatly (Ottusch & Rockwell, 1991). However, the conclusion of the experiment is that for a small SBS signal, the reflectivity and fidelity are both high. To reduce the intensity at the focal point, the F number of the focusing lens should be increased. The similar method is to expend the beam size with a given length of the lens.

4. CONCLUSION

The measurement of phase conjugation fidelity is important for the study of SBS phase conjugation. However, fidelity, especially for the high pump energy, is difficult to measure experimentally. By the method of array camera, for the measurement of fidelity, the focus spot of the input beam is divided into array spots. Unlike the method of the energy-in-the-bucket technique, a great error results from the plasma closure in the focal pinhole irradiated by the focused beam. The principle of this measurement is described in detail. By this method, the fidelity at high pump energy is measured in experiment. The maximum energy of the incident pulse is 3.42 J and the intensity is 21 MW/cm2, which is far more than the threshold of SBS initiation. At the same time, the energy reflectivity is measured, too. For low pump energy, the reflectivity grows exponentially, and the fluctuation is not observed. Thus, the fidelity maintains a high value of more than 0.9. However, the reflectivity fluctuation is significant when the pump energy is more than 1.5 J. As a result, the fidelity decreases gradually to 0.5 at the pump energy of 3.42 J. In applications, high reflectivity, and consistently good phase conjugation fidelity are required for high energy pump beams, so an increase of the size and a reduction of the intensity of the input beams are preferred.

ACKNOWLEDGMENTS

This work is supported by the National Natural Science Foundation of China (Grant No. 60878005), the National High Technology Development Program of China and the Program of Excellent Team in Harbin Institute of Technology.

References

REFERENCES

Andreyev, N.F., Khazanov, E.A., Palashov, O.V. & Pasmanik, G.A. (1994). Phase-conjugation fidelity fluctuation for various stimulated-Brillouin-scattering mirror geometries. J. Opt. Soc. Am. B 11, 786–788.CrossRefGoogle Scholar
Brignon, A. & Huignard, J.P. (2003). Phase Conjugate Laser Optics. New York: Wiley.CrossRefGoogle Scholar
Crofts, G.J. & Damzen, M.J. (1991). Steady-state analysis and design criteria of two-cell stimulated Brillouin scattering systems. Opt. Commun. 81, 237–241.CrossRefGoogle Scholar
Dane, C.B., Neuman, W.A. & Hackel, L.A. (1992). Pulse-shape dependence of stimulated-Brillouin-scattering phase-conjugation fidelity for high input energies. Opt. Lett. 17, 1271–1273.CrossRefGoogle ScholarPubMed
Dane, C.B., Neuman, W.A. & Hackel, L.A. (1994). High-energy SBS pulse compression. IEEE J. Quan. Elect. 30, 1907–1915.CrossRefGoogle Scholar
Hasi, W.L.J., Lu, Z.W., Li, Q. & He, W.M. (2007). Research on the enhancement of power-load of two-cell SBS system by choosing different media or mixture medium. Laser Part. Beams 25, 207–210.CrossRefGoogle Scholar
Kappe, P., Strasser, A. & Ostermeyer, M. (2007). Investigation of the impact of SBS-parameters and loss modulation on the mode locking of an SBS-laser oscillator. Laser Part. Beams 25, 107–116.CrossRefGoogle Scholar
Kong, H.J., Yoon, J.W., Beak, D.H., Shin, J.S., Lee, S.K. & Lee, D.W. (2007). Laser fusion driver using stimulated Brillouin scattering phase conjugate mirrors by a self-density modulation. Laser Part. Beams 25, 225–238.CrossRefGoogle Scholar
Kong, H.J., Yoon, J.W., Shin, J.S., Beak, D.H. & Lee, B.J. (2006). Long term stabilization of the beam combination laser with a phase controlled stimulated Brillouin scattering phase conjugation mirrors for the laser fusion driver. Laser Part. Beams 24, 519–523.CrossRefGoogle Scholar
Lehmberg, R.H. (1982). Numerical study of phase conjugation in stimulated backscatter with pump depletion. Opt. Commun. 43, 369–374.CrossRefGoogle Scholar
Lontano, M., Passoni, M., Riconda, C., Tikhonchuk, V.T. & Weber, S. (2006). Electromagnetic solitary waves in the saturation regime of stimulated Brillouin backscattering. Laser Part. Beams 24, 125–129.CrossRefGoogle Scholar
Meister, S., Riesbeck, T. & Eichler, H.J. (2007). Glass fibers for stimulated Brillouin scattering and phase conjugation. Laser Part. Beams 25, 15–21.CrossRefGoogle Scholar
Ostermeyer, M., Kong, H.J., Kovalev, V.I., Harrison, R.G., Fotiadi, A.A., Megret, P., Kalal, M., Slezak, O., Yoon, J.W., Shin, J.S., Beak, D.H., Lee, S.K., Lu, Z., Wang, S., Lin, D., Knight, J.C., Kotova, N.E., Straber, A., Scheikhobeid, A., Riesbeck, T., Meister, S., Eichler, H.J., Wang, Y., He, W., Yoshida, H., Fujita, H., Nakatsuka, M., Hatae, T., Park, H., Lim, C., Omatsu, T., Nawata, K., Shiba, N., Antipov, O.L., Kuznetsov, M.S. & Zakharov, N.G. (2008). Trends in stimulated Brillouin scattering and optical phase conjugation. Laser Part. Beams 26, 297–362.CrossRefGoogle Scholar
Ottusch, J.J. & Rockwell, D.A. (1991). Stimulated Brillouin scattering phase-conjugation fidelity fluctions. Opt. Lett. 16, 369–371.CrossRefGoogle Scholar
Schelonka, L.P. & Clayton, C.M. (1988). Effect of focal intensity on stimulated-Brillouin-scattering reflectivity and fidelity. Opt. Lett. 13, 42–44.CrossRefGoogle ScholarPubMed
Suni, P. & Falk, J. (1987). Measurements of stimulated Brillouin scattering phase-conjugate fidelity. Opt. Lett. 12, 838–840.CrossRefGoogle ScholarPubMed
Vlad, V., Eichler, H.J., Babin, V., Mocofanescu, A., Riesbeck, T. & Riesse, E. (2004). High reflectivity and fidelity SBS phase conjugation mirrors for solid state lasers. Proc. SPIE 5581, 571–581.CrossRefGoogle Scholar
Wang, S.Y., Lu, Z.W., Lin, D.Y., Ding, L. & Jiang, D.B. (2007). Investigation of serial coherent laser beam combination based on Brillouin amplification. Laser Part. Beams 25, 79–83.CrossRefGoogle Scholar
Yoshida, H., Fujita, H., Nakatsuka, M., Ueda, T. & Fujinoki, A. (2007). Temporal compression by stimulated Brillouin scattering of Q-switched pulse with fused-quartz and fused-silica glass from 1064 nm to 266 nm wavelength. Laser Part. Beams 25, 481–488.CrossRefGoogle Scholar
Yoshida, H., Kmetik, V., Fujita, H., Nakatsuka, M., Yamanaka, T. & Yoshida, K. (1997). Heavy fluorocarbon liquids for a phase-conjugated stimulated Brillouin scattering mirror. Appl. Opt. 36, 3739–3744.CrossRefGoogle ScholarPubMed
Figure 0

Fig. 1. Schematic of the array camera for measuring far-field distribution (a) and focal spot array acquired by CCD (b).

Figure 1

Fig. 2. The far-field distribution of Gaussian beam.

Figure 2

Fig. 3. The dependence of energy ratio of the pump energy or the SBS energy in different far-field angle to the total energy by the array camera.

Figure 3

Fig. 4. Experimental layout used to measure the SBS phase conjugation fidelity by the “array camera” technique.

Figure 4

Fig. 5. Energy reflectivity as a function of high pump energy.

Figure 5

Fig. 6. Phase conjugation fidelity as a function of pump energy.