1. INTRODUCTION
A series of high uniformity spherical implosion experiments
has recently been conducted on the OMEGA laser system in
the University of Rochester (Marshall et
al., 2000; Meyerhofer et al.,
2001). In these experiments, 3–15 atm deuterium
(D2)-filled plastic shells of diameter ∼1 mm were
irradiated with 1-ns square laser pulses of total energy ∼20 kJ.
Fusion yields were measured experimentally to be 10–50% of
one-dimensional (1D) numerical simulations' prediction. It is
believed this is mainly due to core–shell mixing.
Unlike full-scale inertial confinement fusion (ICF) implosions, which
aim to attain a self-sustaining fusion reaction (Lindl, 1995), the experiments under consideration
here are scaled down to the energy of the OMEGA laser system, and are
not planned to achieve ignition. The fusion rate in these experiments
depends strongly on the spherical symmetry of converging shock waves,
which heat and compress the gas. Therefore, the effect of perturbations
and of turbulent mixing on these implosions is different than their
effect on ICF ignition, as has been investigated by Kishony and Shvarts
(2001).
During the shell acceleration, a wide spectrum of perturbations
reaches the inner shell interface, and then grows due to the
Rayleigh–Taylor instability (RTI) during the deceleration (Sharp, 1984; Lindl,
1995). The perturbations in these implosions include inner and
outer surface roughness, beam-to-beam power imbalance, and single-beam
laser nonuniformity, which has been reduced to a minimal level using 1
THz two-dimensional smoothing by spectral dispersion (2D-SSD; Skupsky et al., 1989). During the
acceleration stage, perturbations on the outer interface of the shell
grow due to the ablative RTI and feed-through to the inner interface.
The most dominant inner surface perturbation at the beginning of the
deceleration originates from power imbalance, which has a spherical
mode number of ∼6–10. Shorter wavelength perturbations are
stabilized by the ablation, and their feed-through is less
effective.
The RTI growth of these perturbations during the deceleration induces
a strong shear in the flow, which initiates a secondary
instability—the Kelvin–Helmholtz instability (KHI). The
rate of nuclear fusion in the mix region is reduced due to cooling down
of the hot gas when mixed with the cold plastic shell. Moreover, if
fully developed turbulence is reached, mixing occurs down to the atomic
scale, and the effective gas density is reduced, hence reducing the
fusion rate. Direct numerical simulations describe only structures
larger than the computational mesh size and normally do not include a
physical mechanism causing mixing on smaller scales. Therefore, they
describe the cooling of the gas only partially and do not describe the
decrease in gas density. This calls for further modeling of the fully
mixed region and of the fusion reactions in it. Empirical modeling of
turbulent mixing is based either on two-phase flow (Youngs, 1984, 1989, 1994) or on dissipation of kinetic energy (Gauthier & Bonnet, 1990). A simple bounding
estimate for the yield degradation, valid in the short wavelength
limit, is obtained by assuming there are no fusion reactions in the mix
region (Levedahl & Lindl, 1997).
The neutron yield degradation is customarily quantified by the ratio
between the experimental yield and the yield in a one-dimensional (1D)
simulation without mixing, and is denoted “yield over
clean” (YOC). It has been realized that the convergence ratio
(CR) of the implosion is one of the central factors determining the
growth of a mix region, which in turn determines the YOC (Marshall
et al., 2000, Meyerhofer et
al., 2001, Radha
et al., 2002). We chose to concentrate on two typical
experiments, which represent two extreme CRs. The experimental data is
summarized in Table 1. The 3-atm case has a
larger CR than the 15-atm case, implying more mix growth, hence a
smaller YOC. This article attempts to explain both the YOC values and
their dependence on the CR using these two specific experiments.
Because the shell diameter and thickness and the laser conditions are
similar in both experiments, the acceleration stage is similar. This
implies similar perturbation growth and feed-through up to the
deceleration stage, and allows a comparison mostly of the RTI unstable
deceleration stage and fusion.
Modeling turbulent mixing in ICF. Summary of data for the two
experiments under consideration in the paper.
2. HYDRODYNAMIC SIMULATIONS
The growth of perturbations due to the RTI is calculated using full
two-dimensional (2D) hydrodynamic simulations with LEEOR2D. The
simulations include separate temperatures for the ions and the
electrons, a Thomas–Fermi equation of state for the electrons,
and an ideal gas equation of state for the ions, electron heat
conduction, and fusion reactions. The perturbation growth and
feed-through during the acceleration stage is calculated using a
postprocessor developed by Goncharov et al. (2000). The 2D simulations begin at the end of the
acceleration stage by imposing on a 1D radial profile this multimode
spectrum of perturbations as a modulation in the velocity field.
The result of a 1D spherical symmetric simulation with LEEOR2D for
the 15-atm case is displayed in Figure 1. A
first shock converges to the center at t ∼ 1.6 ns, and
causes an initial rise in the neutron production rate to
∼3e19 s−1. This shock reflects from the
center, hits the shell interface at t ∼ 1.7 ns, and then
converges again to the center at t ∼ 1.8 ns, causing a
second rise in the neutron production rate to ∼1e21
s−1. A third weaker shock converges to the center at
t ∼ 1.9 ns, and raises the neutron production rate to the
maximal level of ∼4e21 s−1. Figure 2 displays the result of the 2D simulation
for this 15-atm implosion, including the full spectrum of
perturbations. Up to t ∼ 1.7 ns, the shell is quite
symmetric, however from t = 1.8 ns, the growth of
perturbations can be clearly seen. These perturbations are dominated by
mode number 6, which originates mostly from power imbalance. By
t = 2 ns, the cold plastic spikes almost reach the center of
the hot gas bubble. Because the peak of the fusion rate is at
t ∼ 1.9–2 ns, these perturbations are expected to
have a large effect on the neutron yield. Figure
3 displays the result of the 2D simulation for the 3-atm case,
in which perturbation growth is qualitatively similar. However, due to
the smaller gas pressure, the stagnation is at a smaller radius and the
mixing zone grows to a larger extent.
Result of a 1D simulation for the 15-atm case. The colormap denotes
density [gr/cm3] versus radius and time. Also
plotted are the gas-shell interface (solid line) and the neutron
production rate on a logarithmic scale (dashed line).
Temporal evolution of gas–shell interface in a 2D simulation of
the 15-atm case. The thin line corresponds to t = 2 ns, when
peak neutron production occurs.
Temporal evolution of gas–shell interface in a 2D simulation of
the 3-atm case. The thin line corresponds to t = 2.1 ns, when
peak neutron production occurs.
Neutron yield is smaller in 2D simulations as compared to the 1D
simulations, as can be seen for both implosions in Figure 4. When the first shock emerges from the
shell interface it is nearly unperturbed. Thus, the shock converges
very symmetrically, and the rise it causes to the neutron production
rate is not affected by the perturbations. By the time the first shock
is reflected from the center and reaches the interface again there is a
small perturbation on the interface. Hence, the second shock reflected
from the interface and converging to the center is slightly perturbed.
This results in a reduction of the second rise in the neutron
production rate by a factor of ∼2. When the second shock reaches
the interface, it has a large perturbation on it, and the convergence
of the third shock is strongly affected. The sharp rise in the neutron
production rate at the convergence of the third shock to the center can
hardly be seen in the 2D simulations. The maximal neutron production
rate is reduced by a factor of 2.7 for the 15-atm case and by a factor
of 3.4 for the 3-atm case. The integrated neutron yield is reduced by a
factor of ∼2 for the 15-atm case and by a factor of ∼3 for the
3-atm case.
Neutron production rate versus time for (a) 15 atm and (b) 3 atm.
Plotted are the results of 1D simulations (solid lines), of 2D
simulations (dashed lines), and of 2D simulations with the simple
mixing model (dotted lines).
These simulations describe the mixing between the gas and the shell
only on length scales larger than the computational mesh size. To
describe mixing of smaller structures, we define the mix region as the
region between the radius, Rspike, of the
spike that has penetrated most deeply into the gas, and the radius,
Rbubble, of the bubble that has penetrated
most deeply into the shell. Following the 1D modeling of Levedahl and
Lindl (1997), we assume this entire region is
fully mixed due to secondary instabilities. The full-mixing model is
attained from the 2D simulations by assuming fusion reactions only in
the central clean region. This model results in a reduction in the
total neutron yield by another factor of ∼2 for the 15-atm case and
by a factor of ∼3 for the 3-atm case. The reduction due to this
model grows with time due to the growth of the extent of the mix
region, as can be seen in Figure 4.
These results are summarized and compared to the experimental results
for the two implosions in Figure 5. The 2D
simulations underestimate yield degradation, and the simple mixing
model overestimates it. However the CR dependence of both the 2D
simulations without mixing and with the simple mixing model is similar
to that found in the experiments. For the 15-atm case, which has a
smaller CR, the yield resulting from the simple mixing model is lower
by a factor of ∼2 than the yield assuming no mixing. This reflects
the fact that half of the yield is from the mix region and half from
the clean region. For the 3-atm case the yield is reduced by a factor
of ∼3, indicating that only one-third of the yield in the 2D
simulation is from the clean region.
YOC versus CR for experiments (circles), 2D simulations (squares),
simple mixing model (diamonds), and modified mixing model
(triangles).
3. ANALYSIS OF SIMULATIONS
To analyze the differences between the 1D and 2D simulations, we
define the cumulative fusion rate as the spatial integral of the fusion
rate:
where n(r, t) is the fusion rate as a
function of the location vector, r, and time, t.
Figure 6 displays N(R) for
the 1D and the 2D simulations for the two cases at the peak neutron
production rate. Simulation results are normalized to the 1D neutron
rate. In the 1D simulation, N(R) is a smooth rising
function. In 2D, we observe several features. The central region is
clean and behaves qualitatively like the whole 1D bubble; however, the
yield from it is higher than the yield from the same region in the 1D
simulation. This feature can more clearly be seen for the 15-atm case.
The rise in the cumulative fusion rate in the central region ends
gradually at a radius slightly larger than
Rspike. Then, throughout most of the mix
region there is a small contribution to the cumulative fusion rate, and
before Rbubble, there is a second rise due
to the gas bubbles that have penetrated the plastic shell due to the
RTI.
The cumulative fusion rate normalized to the 1D rate versus radius
for (a) the 15-atm case at t = 1.95 ns and (b) the 3-atm case
at t = 2.05 ns. The 2D simulations (solid line) are compared
to the 1D simulations (dashed line). The vertical lines denote
R1D, Rbubble,
and Rspike.
Perturbations change the dynamics of shock waves during the
compression, and generally cause them to be less sharp and to converge
less singularly to the center, hence degrading efficiency of heating
and compression. On the other hand, due to these nonsharp shocks, the
entropy remains lower than in 1D, allowing for a more efficient
compression. The higher yield from the central region in 2D results
from a higher density attained there. These differences in central
pressure, density, and fusion rate imply that mix effects are not
limited to the mix region, and may not be described by effective 1D mix
models. This occurs for the specific implosions under consideration
here, which had high perturbation amplitudes and were dominated by low
mode numbers.
The smaller slope of N(R) in the mixing region is
partly because less gas mass is present there and partly because fewer
fusion reactions occur in this mass. To separate these two effects, we
plot in Figure 7 the cumulative fusion rate
at the peak neutron production rate as a function of cumulative
mass:
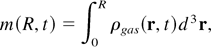
where ρgas(r, t) is the gas
density as a function of r and t.
The cumulative fusion rate normalized to the 1D rate versus mass for
(a) the 15-atm case at t = 1.95 ns and (b) the 3-atm case at
t = 2.05 ns. The 2D simulations (solid line) are compared to
the 1D simulations (dashed line). The vertical lines denote
Rclean for f = 0
(Rclean =
Rspike) and f =
0.2.
The central 20–25% of the mass behaves similarly in 1D and in
2D, implying that the difference in the central region observed above
was mainly due to flow of more mass into the center and not from a
change in the fusion rate per unit mass. For the rest of the gas there
is a gradual increase in the cumulative fusion rate at a smaller rate
compared to 1D. This reduced fusion rate per unit mass is purely due to
the presence of the perturbations, and not due to less mass being
present as may be inferred from the radial profiles presented in Figure 6. These features of mass flow into the
center and of thin tubes connecting the bubbles to the central clean
region may be typical only for implosions dominated by long-wavelength
perturbations. Whenever such differences between the 1D and 2D radial
profiles occur, care should be taken when combining models for
calculating the extent of the mix region with 1D simulations. The
behavior of the fusion rate as a function of mass implies that in such
modeling it is more important to reproduce the correct mass
distribution than the correct radial distribution.
4. ESTIMATES OF MIXING
We expect the secondary instabilities to cause turbulent mixing in
the region occupied by the large-scale bubbles and spikes generated by
the RTI. Figure 8 displays the gas shape at
peak compression with the vorticity of the flow, defined as
ω = ∇ × u, where u is the
velocity vector. The KHI is expected to grow as,
dKH ≈ 0.1ΔuΔt (Brown & Roshko, 1974), where Δu =
ωΔx is the shear in the velocity, Δx is
the typical length scale of the shear, and Δt is the time
scale for the instability growth. In this case, ω reaches 100
ns−1 and Δt ≈ 0.1 ns; therefore
dKH ≈ Δx. This means that we should
expect the vortices to grow to the size of the perturbation scale
described in the simulations, and regions with high vorticity are
expected to be mixed due to the KHI. The simple full-mixing model
defines Rclean =
Rspike and assumes all the regions with
r > Rclean are fully mixed.
This definition does include all the region between the bubbles and the
spikes, but also includes the wide bases of the bubbles, where the
shear in the velocity is smaller by an order of magnitude than the
shear in the expected mix region. Regions with such small shear are not
expected to be mixed due to the KHI. Without a detailed mixing model
based on KHI, we suggest a simple crude estimate by defining the mix
region with Rclean slightly larger than
Rspike. In this manner only the expected
mix region will be included, and the expected clean region will not be
affected by the mixing model. Figure 8
demonstrates how increasing Rclean
slightly results in a good definition of the mixing region.
Contours of vorticity [ns−1] for the
15-atm case at t = 2 ns. The thick solid line denotes the
gas–shell interface and the two dashed circles denote the simple
(f = 0) and modified (f = 0.2) definitions for the
clean region.
We now define Rclean =
Rspike + f
(Rbubble −
Rspike), where f is a free
parameter. Figure 9 displays the YOC as a
function of this parameter, f. There is a dramatic rise in the
YOC value around f = 0, which corresponds to the simple mixing
model. This rise continues up to f ∼ 0.2, where the tubes
connecting the bubbles to the central region get very thin. The second
rise from f ∼ 0.7 to f = 1 (no small-scale
mixing) is due to the bubbles. If we assume the bubbles and the tubes
connecting them to the central region are fully mixed, we should define
Rclean with f ∼ 0.2. A
correction to the mixing model is suggested by choosing the value of
f, where the bubbles' bases end and where the steep rise
in the YOC ends. In both implosions under consideration here, a value
of f ∼ 0.2 should be taken. This single value of
f identifies the high vorticity zones for both implosions
because both have similar spectra of perturbations and similar
vorticity maps. This is not a general result, and it should be
reconsidered for every specific implosion and perturbation spectrum.
YOC versus f, where f defines
Rclean as
Rclean =
Rspike + f
(Rbubble −
Rspike). The solid line represents the
15-atm case and dashed line represents the 3-atm case. The vertical
lines denote the simple (f = 0) and modified (f =
0.2) definitions for the clean region.
We modify the mixing model by taking f = 0.2. In this manner
only the regions theoretically expected to be mixed are included, and
the YOC values are between the overestimate of the 2D simulation
without mixing to the simple mixing model. The modified YOC values are
in good agreement with the experimental results, as can be seen in
Figure 5.
5. CONCLUSIONS
Recent ICF experiments have been analyzed by comparing the
experimental results with full 1D and 2D numerical simulations for
implosions with two extreme CRs. Differences in central pressure,
density, and fusion rate at high perturbation amplitudes imply that mix
effects are not limited to the mix region, so that care should be taken
when describing them by effective 1D mix models. Assuming no mixing
beyond the length scales described in the 2D simulations, the bubbles
raise fusion yield above experimental results, whereas assuming a
simple full-mixing model overestimates yield degradation. The problem
with the simple mixing model is that regions slightly beyond the clean
radius contribute significantly to fusion yield, while they are
expected not to be mixed due to the KHI. The mixing model is therefore
modified by redefining the clean radius according to crude estimates
based on vorticity maps in the 2D simulations, resulting in improved
agreement with experimental results for a wide range of CRs.
The implosions investigated in this paper were dominated by low mode
number perturbations, originating mainly from power imbalance between
the various laser beams. This implies a difficulty in describing both
the mix region and the central clean region by effective 1D models.
Implosions with a reduction in this perturbation have been investigated
by 2D simulations, and were found to behave differently. The
perturbations generated by the RTI have a wider spectrum of mode
numbers, so that bubble competition plays a central role in driving the
evolution into a self-similar regime, where effective models for the
calculation of the mix region may again be applied. Moreover, for
implosions dominated by high mode number perturbations less large-scale
flow into the central region is expected, and 1D simulations together
with models such as that of Levedahl and Lindl (1997) may be adequate to describe the turbulent
mixing.
It has been found that perturbations cause shock waves to be less
sharp; hence, the entropy remains lower and the compression of the
central region is more effective. This effect causes it to differ from
the corresponding symmetric implosion. This effect should be further
investigated both for these implosions and for more general cases.
Simulations and modeling of mixing were compared to experiments
through one measured parameter—the neutron yield. However, more
parameters, such as fuel areal density and temperature may be deduced
from the experiments and compared to theoretical models, as has been
done by Meyerhofer et al. (2001) and
by Radha et al. (2002).
All mix analysis has been conducted as a postprocessing of the
hydrodynamic simulations. In reality, the evolution of the turbulent
mixing affects the large-scale dynamics and should be taken into
account with a feedback to the hydrodynamic simulation. In this manner
the level of mixing in every region may be evaluated more precisely.
ACKNOWLEDGMENTS
The authors thank the Laboratory for Laser Energetics at the
University of Rochester for their hospitality and partial support
during this work. Special thanks are given to D.D. Meyerhofer and P.B.
Radha for supplying the experimental results, to V.N. Goncharov and P.
McKenty for generating initial conditions for the simulations, and to
D. Oron for helpful remarks.
