Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T14:19:20.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Microwave emission from TW-100 fs laser irradiation of gas jet

Published online by Cambridge University Press:  05 December 2005

DAVOUD DORRANIAN ,
MAHMOOD GHORANNEVISS ,
MIKHAIL STARODUBTSEV ,
NOBORU YUGAMI  and
YASUSHI NISHIDA
DAVOUD DORRANIAN
Affiliation:
Plasma Physics Research Center, Science and Research Campus, Islamic Azad University, Poonak, Tehran, Iran
MAHMOOD GHORANNEVISS
Affiliation:
Plasma Physics Research Center, Science and Research Campus, Islamic Azad University, Poonak, Tehran, Iran
MIKHAIL STARODUBTSEV
Affiliation:
Institute of Applied Physics RAS, Nizhny Novgorod, Russia
NOBORU YUGAMI
Affiliation:
Graduate School of Engineering, Utsunomiya University, Utsunomiya Tochigi, Japan
YASUSHI NISHIDA
Affiliation:
Graduate School of Engineering, Utsunomiya University, Utsunomiya Tochigi, Japan
Rights & Permissions [Opens in a new window]

Abstract

A new kind of high power tunable microwave radiation source is studied theoretically and experimentally. Following the previous works presented by Dorranian et al. (2003, 2004) in this paper more details about the radiation is presented. The theory of the radiation is developed to calculate the radiation spatial distribution, and more discussion on radiation behavior and characteristics is done. In this radiation scheme, a part of large amplitude electrostatic plasma wake, generated by an intense laser pulse or a relativistic electron bunch, are converted to electromagnetic oscillations by applying a modest dc magnetic field perpendicular to the wake propagation direction. A direct one-dimensional (1D) analytic procedure for calculating the magnetized plasma wake equations is developed and the properties of the radiation are investigated theoretically. The effects of the ramp plasma-vacuum boundary in coupling the radiation from plasma to vacuum is noticed and solved by employing a gas jet flow to generate a sharp boundary. Wakefield is excited by TW-100 fs Ti:sapphire laser beam operating at 800 nm wavelength. The neutral density of gas jet flow is measured with a Mach-Zehnder interferometer. The frequency of the emitted radiation with the pulse width of 200 ps (detection limitation) is in the millimeter wave range. Radiation is polarized perpendicularly to the dc magnetic field lines and propagates in the forward direction and normal direction with respect to the laser pulse propagation direction, both perpendiculars to the direction of the applied magnetic field. Intensity of the radiation in different plasma densities and different magnetic field strengths has been observed.

Keywords

Extra ordinary modePonderomotive forceSharp/ramp boundaryWakefield
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 4 , October 2005 , pp. 583 - 596
Copyright
© 2005 Cambridge University Press

1. INTRODUCTION

The use of TW and higher power laser pulses of picosecond or shorter duration led to many new phenomena at the interaction with lasers including electron beam with 100 MeV and higher energy, 10 MeV intense gamma bursts new categories of nuclear reactions and fusion ignition at modest compression (Hora et al., 2002; Hora, 2004). Even for the generated microwave emission, several new phenomena were observed (Dorranian et al., 2003, 2004; Yoshii et al., 1997; Yugami et al., 2002), where further developments are reported in the following.

Large amplitude waves in a multi mode media such as plasma (Katsouleas & Bingham, 1996; Osman et al., 2004) is a great source of energy. Up to now the energy of these wakes were used for different purposes such as particle acceleration or radiation (Korovin et al., 2003; Mesyats, 2003; Gushenets et al., 2003). Theories and experiments have shown that plasma is a capable medium to convert different initial energies to coherent radiation, i.e., Raman scattering, harmonic generation, and photon acceleration (Dodin & Fisch, 2002; Lin et al., 2002; Ji, 2001). This possibility comes from the multi-mode nature of the plasma. We are studying a new kind of high power tunable radiation source. In this radiation scheme, interaction between the laser pulse and the plasma causes the ponderomotive force and generates the Wakefield at the frequency of ωp so, tunable with varying the plasma density. The initial motions of plasma electrons make them rotate around the magnetic field lines and generate the electromagnetic (EM) part in the wake with a nonzero group velocity. The magnetized wake propagates through the plasma and couples to vacuum at the plasma-vacuum boundary. The advantage of this radiation source is its frequency tunability. By increasing the plasma density, a new source of Terahertz radiation can be generated. Terahertz radiation is non-ionizing electromagnetic radiation with sub-millimeter wavelength which is difficult to be generated and detected. THz rays have applications in biological imaging, material screening, semi-conductor imaging, surface chemistry, and high-field condensed matter studies. Laser-triggered solid-state based sources of THz radiation have been developed that rely on switched photoconducting antennas or optical rectification of femtosecond pulse trains. Large aperture biased GaAs structures, operated at 1 kHz repetition rate, have produced on the order of 0.5 μJ/pulse. Most other sources using either laser switched structures or optical rectification have operated at high frequency (10s of MHz) with μW-mW level average power.

The theory of radiation from the wakes excited by laser pulse in the magnetized plasma was introduced by Yoshii et al. (1997). The characteristics of this radiation have been observed by Yugami et al. (2002) in a gas filled chamber and the first experiment on using gas jet plasma to excite the radiation is reported by Dorranian et al. (2003, 2004).

In this paper, the magnetized plasma Wakefield experiments are discussed in detail. After the introduction in Section 1, the theory of the radiation is presented in Section 2. Sections 3 and 4 are devoted to interferometry experiments and radiation experiments, respectively. Section 5 is our discussion and Section 6 will present our conclusion.

2. THEORY

2.1. Magnetized Wakefield equation

Since the plasma Wakefield equations are well known, here it is convenient to review the theory presented originally by Yoshii et al. (1997), modified by us after taking into account our experimental conditions. In contrast to the original theory, where all transversal components of the magnetized wake have been found through perturbation technique, we have developed a direct analytical procedure, which allows us to find exact expressions for all components of magnetized plasma wake. These expressions can be used for any driver velocities as well as for any ratios of ωc/ωp. Laser pulse is assumed to propagate in the z direction and external dc magnetic field is applied in the y direction (Fig. 5). This field is uniform in space and constant in time. Maxwell's equations for plane waves in one dimension for the present geometry have the form in the first order relationship:

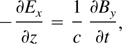
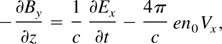
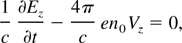
where E and B are radiation fields, n0 is the plasma density and Vx and Vz are the components of electron velocity. The equations of motion are given as:

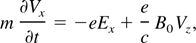
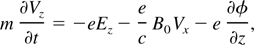
where B0 is the applied external dc magnetic field and φ is the average ponderomotive potential defined by the laser pulse envelope. It can be assumed that the potential φ and therefore the fields and electron velocity are functions of only ξ = t − z/v0, where v0 is the initial phase velocity of the Wakefield. Here a pump depletion and laser instabilities are neglected. In terms of new variable, ∂/∂t → ∂/∂ξ and ∂/∂z → −(1/V0)∂/∂ξ, we have

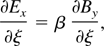
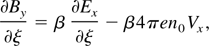
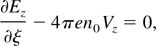
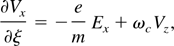
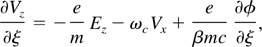
where ωc is the electron cyclotron frequency and β = V0 /c. Applying Laplace transformation with respect to ξ, the set of above equations become

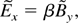
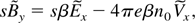
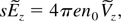
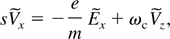
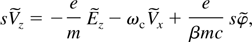
where the tilde refers to Laplace transformation of variables, s is the Laplace variable, and

is the Laplace transformation of φ. Answers for this set of equations are given as

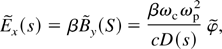
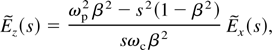
where ωp and ωc are the plasma and electron cyclotron frequency, respectively. D(s) = [εβ2ωp2 − (1 − β2)(s2 + ωp2 + ωc2)] and ε = 1 + ωp2/s2. To find the components of the excited magnetized Wakefield behind the laser pulse, we have to take the inverse Laplace transformation of the above equations. They are described by the residue of Eq. (16) at the pole where D(s) = 0. The dispersion equation which will be given by D(iω) = 0 defines the frequency ω of the Wakefield. The amplitude of the By field is given at the pole s = iω and takes the following form

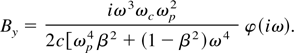
For a laser pulse of the duration τ, electric field EL, and frequency ωL, the ponderomotive potential has the form φ = eEL2/4mωL2. Transforming it to ω space, we have

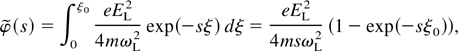
in which ξ0 = τL − z/v0. τL is the laser pulse duration. For s = iω it can be written as

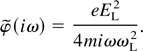
For the transverse and longitudinal components of the magnetized Wakefield, the electric field can be expressed via the relations

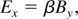
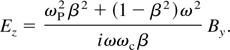
After taking into account the contribution of another pole at s = −iω, the final relation for magnetized Wakefield can be expressed with the relation

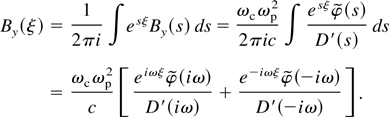
By simplifying the equation, substituting it in Eqs. (21) and (22), the transverse and longitudinal components of the magnetized Wakefield can be obtained as

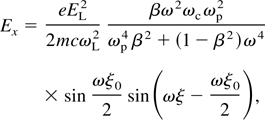
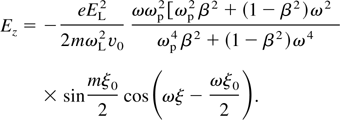
These equations can be used for any radiation driver i.e., electron bunch or laser pulse with different velocities.

When ωp >> ωc is assumed as will be described in Section 6 in the present experimental conditions, one obtains

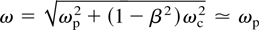
for the radiation frequency and Eqs. (24) and (25) are converted to

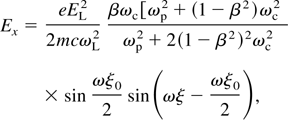
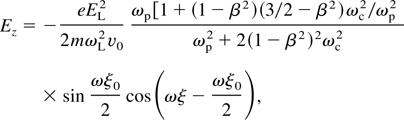
applying more simplification it can be written as

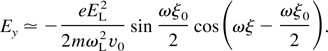
In this case ωH ≃ ωp and the dispersion relation reduces to c2k2/ω2 ≃ 1 − ωp2/ω2, resulting in the ratio of EM component of the field to ES component

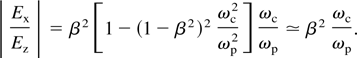
For the two-dimensional (2D) case, the same method is used to derive the equations of magnetized plasma Wakefield (Bakunov et al., 2003).

2.2. Radiation from magnetized Wakefield

By applying the external magnetic field a new component will be added to the Wakefield, as it has been described in the former section.

Before coming to this phenomenon there were two known mechanisms of the plasma based radiation sources. First one is called the “inverse mode conversion” (Ginzburg, 1970). Another is the radiation due to “charge separation” mechanism (Hamster et al., 1993). In our case the scenario is completely different. Geometry of the radiation can be found in Figure 1. The laser pulse propagates in the +z direction. The plasma Wakefield due to intense laser pulse-plasma interaction propagates with the group velocity of the laser pulse (≈ c) in the same direction as the laser does in one-dimensional (1D) limit. In unmagnetized plasma, the Wakefield is completely electrostatic. By applying a modest perpendicular dc magnetic field B0 in the y direction, the Wakefield finds an electromagnetic component with non-zero group velocity at the frequency close to ωp, so this component of the Wakefield is enabled to propagate through plasma into the vacuum. The initial motion of plasma electrons due to the laser ponderomotive force makes them to rotate around the magnetic field lines in the (x,z) plane and generates the electromagnetic part of the Wakefield, Ex. In Figure 1, the schematic view of radiation generation is shown. Since the radiation frequency is very close to plasma frequency so it is tunable with plasma density.

Schematic view of EM radiation generation.

2.3. Radiation pattern

To describe the radiation pattern one can start from the current equation.

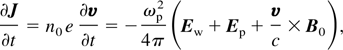
where Ew is the Wakefield, Ep is the laser ponderomotive electric field and v is the second order perturbed velocity of plasma electrons. We can separate J in Eq. (31) into two irrotational Ji, and solenoidal Js, components,

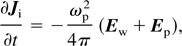
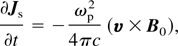
so they satisfy ∇ × Ji = 0 as well as ∇·Js = 0, respectively. Under the Coulomb gauge condition, the vector potential A is determined by the solenoidal current part and the scalar potential φ by an irrotational part. For A it can be written

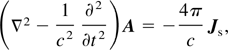
Eq. (34) leads to radiation pattern and spatial distribution. Using Green's function, it is assumed that all the fields are varying with a factor of exp[i(−ωt + k·r)]. Considering the current expression in frequency domain using the Fourier transformation it should be averaged over on the laser pulse duration time τ = σz/vg, as

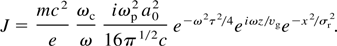
This is the average current intensity corresponding to a laser pulse. Using the far field approximation, the solution of Eq. (34) can be expressed as,

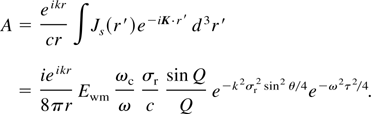
The above integral is located in the region [−σz/2,σz/2]. Here, Q = kσz(1/β − cos θ)/2, β = vg/c, and Ewm = mc2kp2σza02/8e: the maximum amplitude of the Wakefield. From here the magnitude of pointing vector of the radiation can be calculated as

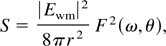
where the radiation pattern F2(ω,θ) is given as

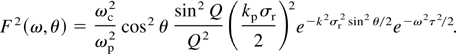
The forward angular distribution of the radiation is shown in Figure 2 for the different radiation frequencies. For plotting the radiation pattern, it is assumed that ωc /ωp = 0.1, kpσz = 2, and σr/σz = 1/3. As it can be seen the main radiation energy concentrates in the forward direction rather than a symmetrical structure for both forward and backward directions. It is because that the Ex component makes a main contribution to the radiation, and vg ∼ c.

Angular distribution of the radiation.

2.4. Radiation dispersion relation

Applying the external magnetic field in the y direction, perpendicular to the laser beam path (in the z direction) and so k ⊥ B0, and also the wave electric field E ⊥ B0, the radiation occurs in the extra ordinary (XO) mode, and the dispersion relation is

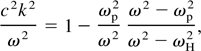
in which ω and ωp are the radiation and plasma frequencies, ωH = (ωp2 + ωc2)1/2 is the upper hybrid frequency, ωc = eB0 /m is the cyclotron frequency of plasma electrons. Dispersion relation has two cutoffs at ωR,L = [±ωc + (ωc2 + 4ωp2)1/2]/2.

In Figure 3 the dispersion relation of Eq. (39) is plotted. The eigenmodes of the plasma are the left-hand polarized (L) and right-hand polarized (R) branches of the XO mode, and have cutoff frequencies at ωL,R, respectively. These two branches have two components to their electric field; an electromagnetic component E = Ex and an electrostatic longitudinal component E = Ez. Waves with ω < ωL and ωH < ω < ωR are evanescent in the plasma. Intersection point of the wave dispersion relation (Eq. (39)) and the laser pulse introduce the radiation frequency. Here it should be noted that the laser wave satisfies ω = kvgl, where vgl = c(1 − ωp2/ωL2)1/2 is the laser pulse group velocity in plasma. The line for laser pulse intersects with the L branch of XO mode in the plasma, where ωp ≤ ω < ωH. In unmagnetized plasma we also have this intersection but the phase velocity of the plasma waves is c while their group velocity is zero. The energy deposited by the laser pulse in unmagnetized plasma does not propagate outside of the plasma but is finally dissipated in the form of plasma heating by collisions. It is noticeable that the line of the laser pulse never intersects with the electromagnetic eigenmode of the plasma (ω2 = ωp2 + k2c2). In the magnetized plasma the group velocity of the excited mode is not zero. Figure 3 shows that the laser pulse can couple to the L-XO mode through the radiation at any angle θ ≤ 90°, where the velocity of the laser pulse vgl ≈ c is larger than the phase velocity of the L-XO mode. Here θ is the angle between the wave vector k of the radiation and the laser pulse propagation direction, and can be defined as cos θ = c/vgl n(ω). Since the plasma is dispersive with the refractive index n(ω) as is defined by Eq. (39), a different frequency can be emitted at different angle. The radiation group velocity decreases for larger propagation angle θ.

Dispersion relation of the magnetized plasma. Evanescent regions are shown by dashed area.

2.5. Boundary condition

Another important parameter is the boundary condition. Non-sharp boundary will make problem for the emitted pulse. As the plasma density decreases at the boundary ωp and ωH will decrease. This will make the evanescent layer wider, which will cover the radiation frequency as it can be seen in Figure. 3. The radiation intensity will be damped noticeably by tunneling through the gradually decreasing density layer. The total damping rate of radiated electric field is calculated by Yoshii et al. (1997). In the case of sharp plasma boundary according to the continuity of the tangential components of E for reflected and transmitted waves, the transmission coefficient for Ex tend to one and the output power of the radiation will be a parabolic function of magnetic field strength. To tend the transmission coefficient field of the radiation to larger by decreasing the attenuation effect due to ramping the plasma density at the boundary, boundary should be as sharp as possible. One of the most advanced ways to achieve this requirement is using the gas jet flow. Controlling the initial neutral density by gas jet back pressure as well as using different kind of nozzles to make a suitable geometry of density interaction medium, has presented some interesting advantages in our experiments. Previous works on gas jet sources has focused on studying homogeneous condensation and making cluster beams (Hagena & Obert, 1972), and after that gas jets are widely used in the field of laser-plasma interaction, in areas such as laser particle acceleration (Modena et al., 1995; Coverdale et al., 1995), inertial confinement fusion (Baton et al., 1998; Denavit & Phillion, 1994), X-ray lasers (Fiedorowics et al., 1994) and high harmonic generation (Fill et al., 1995). Each field requires its special geometry of gas expansion and density configuration. In our case because the magnetized plasma is generated as a source of coherent electromagnetic radiation so the spatial distribution of gas density is key important characteristics specifically uniform gas density inside the flow and sharp boundaries at the interaction region. Because the laser beam passes transversely across the puffed gas area and the radiation from the interaction region should be viewed by the diagnostics, it is also important that the interaction region should be outside of the nozzle with sufficient distance from the tip of the nozzle. The reported works in this area were conducted mostly in very high back pressure range (Li & Fedosejevs, 1994; Malka et al., 2000) but due to our main purpose, which is detecting the radiation from magnetized wake, according to laser pulse width and plasma density relation, the neutral gas densities lower than 1017 cm−3 are interested for obtaining the maximum wake amplitude.

3. INTERFEROMETRY EXPERIMENT

A Mach-Zehender interferometer is employed to measure the neutral gas density as well as the flow configuration. A He-Ne laser beam working at 632 nm is expanded and collimated to a 5 mm diameter beam which propagates in the interferometer. One arm of the Mach-Zehnder interferometer is located in the vacuum chamber in which the gas jet is also positioned and another arm goes through air. The beam splitters and mirrors of the interferometer have a surface quality of λ/10. Outside the vacuum chamber an f/10 spherical len images the gas jet onto a linear charge coupled device (CCD) detector. The spatial resolution is limited by the pixel size about 15 μm. A solenoid valve (model name: Iota one) made by Parker instrumentation with 0.8 mm diameter was employed to generate the gas jet with constant flow of 100–800 ms. The time is always adjusted long enough to record the steady state maximum fringe shift by the CCD and software. These kind of valves are generally closed and the open time can be adjusted from 5 μs to several hours, in frequency or single pulse mode. The back pressure of the gas reservoir is measured by a gas gauge and the pressure in the vacuum chamber was measured by a high quality pirani gauge. In order to study the effect of nozzles on different gas density configurations, different kind of brass nozzles in shape and size are machined. First two are supersonic nozzles at 0.5 mm throat diameter and divergence angle of 12 degree. For bigger one the exit hole diameter is 1.3 mm (a) and for smaller one it is 1 mm (b). Third-one is a simple cylindrical nozzle at 0.5 mm throat diameter (c). Typical patterns of the fringe shifts are shown at the top of Figure 4. They are measured in radians and since the geometry of the nozzle and the medium can be assumed to be cylindrically symmetric, the cylindrical Abel inversion transformation is employed in order to obtain the local density in the gas flow. After the Abel inversion transformation in cylindrical coordinates, the axial data can be changed to radials. Neutral nitrogen gas density of three nozzles with different back pressures are shown in Figure 4. Neutral gas density of nozzle (a) is from 1.5 × 1017 cm−3 to 2.5 × 1018 cm−3 at the center of the flow, and about 0.5 mm upper than the nozzle exit. For nozzle (b) this magnitude changes from 6.5 × 1017 cm−3 to 1 × 1019 cm−3, and for nozzle (c) it is from 2 × 1018 cm−3 to 2.15 × 1019 cm−3 both at the same point. In this range of the back pressure of the supplied gas, the gas density is in a linear function of the back pressure. According to laser intensity of about 1017 W/cm2, gas is expected to be fully ionized and we can calculate the plasma density from neutral gas density. The sharpest boundary between the gas flow and vacuum were found for the case of nozzle (a) at about 0.5 mm from the nozzle tip. In this case, neutral gas density is approximately flat in the radius of about 0.4 mm and fall down to zero within 0.1 mm. We can't generate the ideally sharp boundary due to the quick expansion of the gas flow, which occurs at the nozzle exit. Indeed, this effect occurs due to the very low background pressure in the vacuum chamber, so the flow is said to be “underexpanded” and a subsequent expansion occurs as the flow attempts to meet the necessary boundary condition imposed by the ambient chamber background pressure (Wilcox, 2000).

Interferometer fringe shift of different nozzles are shown at the top. Diamonds on dashed dotted line, squares on dotted lines and circles on dashed line are the neutral gas density magnitudes at different back pressures of nozzles (a), (b), and (c) correspondingly.

Experimental setup.

4. RADIATION EXPERIMENT AND DISCUSSION

4.1. Experimental setup

The experiment was done in the laser laboratory of the energy and environmental science of the graduate school of engineering at Utsunomiya University, Japan.

The experimental arrangement and geometry of the radiation is shown in Figure 5. A mode locked Ti:sapphire laser operating at λL = 800 nm wavelength, with the pulse width of τL = 100 fs full width half maximum (FWHM), and maximum energy of 100 mJ per pulse with 10 Hz repetition rate is used to excite Wakefield. The laser pulse is irradiated into the vacuum chamber through 5 mm thickness CaF2 window in the z direction and is focused by a lens of f/5 at about 0.5 mm above the gas jet nozzle. The focal spot diameter is about 20 μm and the intensity is on the order of 1017 W/cm2. A solenoid valve (Iota one) made by Parker instrumentation with 0.8 mm diameter exit hole was employed to generate the gas jet constant flow of 100–200 μs. The strength of the applied magnetic field is up to 8 kG, uniformly cover the region, much more larger than the interaction region. The experiment is carried out using nitrogen and helium gases at the initial base pressure of below 5 mTorr and maximum gas jet back pressure of 8 atm. At about 5 cm length after the laser beam focal point, a 3 mm thickness teflon plate is used as the beam damper. The measurement system for the radiation consists of a crystal detector, horn antenna, waveguide and oscilloscope (Tektronix; TDS-694C) with limitation of minimum pulse width measurable at 200 ps and covering 10 G sample per second with frequency bandwidth of 3 GHz. Antenna and waveguide in U-band with cut-off frequency at 31.4 GHz for TE10 mode are employed to observe the temporal waveform of the radiation. Radiation is observed in x and z direction due to radial and axial component of magnetized Wakefield.

4.2. Experimental results

4.2.1. Pulse width

In Figure 6 a typical example of the radiation waveform is shown which is obtained from helium plasma at B0 = 7.8 kG corresponding to ωc = 1.4 × 1011 rad/s. The observed pulse duration is of the order of 200 ps at FWHM and limited by the bandwidth of the receiving equipment. In the nitrogen plasma, similar results are also obtained. The life time of the wakes in the plasma can be estimated from τp ∼ Lp/vg, where Lp is the plasma length of the order of Rayleigh length and vg is the group velocity of the wakes in the plasma. In this experiment with laser spot size of 20 μm, Lp is estimated to be about 1.55 mm. The electron density is about 1017 cm−3 correspondingly ωp ≃ 1.8 × 1013 rad/s, so τp is estimated to be about 80 ns, theoretically. But the experimental results show that the Wakefield disappears faster than the calculated life time. In a similar experiment the calculated life time for wakes is about 5.4 ns while the life time of the plasma waves, measured by Thomson scattering, is about 300 ps (Muggli et al., 2002). The reason could be explained by taking into account the gas ionization effect. In the case of preformed plasma, that volume is larger than the laser pulse perturbation volume, a positive charge is created when a corona electron moves away from its original position. This induces a restoring electrostatic force which is proportional to the electron displacement and produce a harmonic oscillator system at the plasma frequency. On the other hand, in the tunnel ionization, the number of positive charges is fixed within the laser pulse radius and Rayleigh length even when the corona electron leaves the plasma. Laser pulse energy is more nonuniform in this volume and electrons feel more nonuniform force. This could induce a lower restoring electrostatic force and larger number of electrons which do not come back in phase with plasma waves and destroy the oscillation faster than the expected time. Similar to this effect for the radial component of plasma Wakefield also was observed by Marques et al. (1998).

Sample of the radiation pulse. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

4.2.2. Polarization and spatial distribution

The polarization of the emitted radiation is measured by rotating the receiver horn antenna around the z axis with angle θ in both cases of He and N2 plasma at different gas densities. As it is predicted by the theory, the electromagnetic component of the Wakefield is in the x direction perpendicular to the direction of the applied external dc magnetic field. An example of the data is presented in Figure 7. Dashed line in Figure 7 indicates the cos2 θ, which is the expected radiation intensity from a tiny dipole antenna oriented along x. Experimental data show that the radiation is also polarized in the x direction, in fairly good agreement with expectation.

Radiation intensity versus the rotation angle of the horn antenna around z direction. Radiation is polarized the x direction. Filled dots are experimental data and dashed line is expectation from the theory. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

The spatial distribution of the radiation is measured by changing the position of the horn antenna in different angles refer to the z axis in the y − z plane. An example of the observed data is shown in Figure 8. The radiation is mainly launched within the angle ±5 degrees with respect to the z axis in the y − z plane in the forward direction. Pulse becomes weaker in larger angles up to ±8 degree and absolutely disappear after that. These results are confirmed by the fact that the group velocity of the magnetized Wakefield is maximum in the forward direction.

Spatial distribution of the emitted radiation. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

4.2.3. Output power of the radiation in different plasma densities

Typical example of the radiation intensity of both He and N2 plasmas in different densities are shown in Figure 9. Gas density is controlled by the back pressure to the gas jet nozzle and density is obtained in the interferometer experiment. Data are obtained by using nozzle (a) at the external magnetic field strength of about 8 kG. The base pressure of the interaction chamber is 15 mTorr and gas jet open time is 250 μs and 10 Hz repetition rate. One can see that the radiation intensity decreases noticeably by increasing the gas density. Radiation from other nozzles show the similar behavior.

Radiation intensity in relative units versus neutral gas density for both He (dotted full square line) and N2 (dashed full circle line) plasma The experiment is done by nozzle (a). B0 ≅ 8 kG.

In Figure 10 three samples of the radiation pulses from different nozzles are displayed for comparison purposes. The position of three radiation pulses are shifted in order to simplify their comparison. Data show the radiation from N2 plasma at 1 atm back pressure in 15 mTorr of chamber pressure and 250 μs gas jet valve open time and 10 Hz repetition rate. Here, the lowest radiation intensity is observed with the nozzle (c) plasma, which generates the largest density and with decreasing the plasma density the radiation has been enhanced as is also evident from Figure 9.

Radiation intensity of three different nozzles at constant gas pressure of 15 MTorr of N0·B0 = 8 kG.

Both data in Figures 9 and 10 verify that increasing the plasma density in this range, will decrease the radiation intensity. These results can be explained due to the fact that in the present experiments we deal with plasma densities greater than the laser Wakefield quasi-resonance. Indeed the term “sin ωξ0 /2” in Eqs. (24) and (26) represents the quasi-resonance behavior of the plasma Wakefield, which confirms that increasing the plasma density from an optimum magnitude will decrease the amplitude of plasma Wakefield. Due to

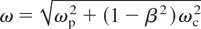
(see Section 2), when ωc << ωp radiation frequency ω is very close to plasma frequency ωp and the maximum Wakefield amplitude is created when cτL = λp, where τL is laser pulse width and λp is the plasma wavelength. In the present experiments, the maximum Wakefield amplitude is expected at 5 THz plasma frequency, corresponding to electron density 3.1 × 1017 cm−3. Increasing the density from this optimum magnitude decreases the wakes amplitude sharply (Marques et al., 1998). The lowest neutral densities of nozzle (a), (b) and (c) are 1.5 × 1017 cm−3, 6.5 × 1017 cm−3, 2 × 1018 cm−3, and plasma electron densities are five times bigger for nitrogen, all of them larger than the optimum magnitudes. Decrease of the Wakefield amplitude with increase of the density when density is larger than optimum density, is in qualitatively reasonable agreement with theory of the plasma Wakefield.

4.2.4. Radiation output power versus magnetic field strength

Relative output power of the radiation versus the external magnetic field is shown in Figure 11. The data are obtained without changing the position of the gas jet nozzle and the laser beam. The magnetic field is varied by changing the distance between the poles of the permanent magnets pair, which are controlled from the outside of the vacuum chamber. The experiment is done by nozzle (a) at the constant back pressure of 1 atm, corresponding to 1.5 × 1017 cm−3 neutral gas density. Working gas is N2. The circles are the average of six data and the error bars indicate the difference between maximum and minimum of the experimental data at each magnetic field strength. From B0 = 0 to 1.7 kG, although the amplitude of the signal is larger than the noise level, the radiation intensity doesn't change significantly with increasing the magnetic field. In this region, magnetic field is weak and unable to affect the plasma Wakefield. The observed radiation in this range of B0 might be caused by nonlinear currents (Hamster et al., 1993). Up to 7.5 kG, the output power of the radiation increases with the magnetic field strength. Solid line indicates the theoretical values. Due to Eqs. (24) and (26) the amplitude of the radiation field is proportional to ωc, or B0. So without taking the damping phenomenon into account, the output power of the radiation is proportional to B02. Because of the sharp boundary of the gas jet plasma, the radiation is emitted without the boundary effect, in contrast to the theory predicted by Yoshii et al. (1997) and experimentally observed by Yugami et al. (2002) (see Fig. 17a) in gas filled chamber. Due to the above mentioned theory of the boundary model, the attenuation of the output power increases with B0 faster than increasing the output power which goes as B02. Until now, the peak in radiation around B0 = 3 kG and 6 kG can not be explained.

Output power of the radiation as a function of the applied external dc magnetic field. Solid line indicates the theoretical values (≈B02). Error bars show the difference between the maximum and minimum of the obtained experimental data.

4.2.5. Radiation frequency

The frequency of the emitted radiation is measured by the method of the “time of flight (TOF).” In this method we measure the TOF of the pulse in different waveguide lengthes, the frequency of the detected pulse can be calculated. The principle of the TOF method by the delay waveguide line is that the group velocity of the microwave in the waveguide depends on its frequency. Therefore we can obtain the frequency of the microwave by measuring the delay time due to the length of different waveguides. Dispersion relation of the radiation in a waveguide is

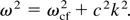
The subscript “cf” refers to cutoff. If it takes t seconds for the pulse propagating through a waveguide of length L, so t = L/vg must be hold, where

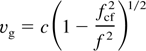
is the group velocity of the pulse and f is the characteristic frequency of each pulse.

Combining the above relations for the frequency term one can write

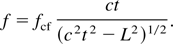
The experimental setup is shown in Figure 12. Typical example of the measured pulses from the radiation at different length of the waveguide can be seen in Figure 13 for N2. Nozzle (a) is used to generate the gas flow at 1 atm back pressure. Measured delay times for 21, 50, and 75 cm length waveguide are 0.85, 1.95, and 2.99 ns, respectively. The cutoff frequency of the waveguide is 31.4 GHz. Using Eq. (42), the estimated frequency of the detected pulse at points (b), (c), and (d) are 54.86, 60.68, and 57.15 GHz, respectively, which leads to the average value of 57.57 GHZ for the emitted radiation. Of course this value is too far from the plasma frequency which is expected to be about 5 THz corresponding to neutral gas density of 1.5 × 1017 cm−3.

Scheme of TOC experiment setup.

Detected pulses at points (a), (b), (c), and (d) of the waveguide. Delay times are referred to point (a).

4.2.6. Pulse broadening

Another observed phenomena in the TOF experiment is pulse broadening. This effect occurs when longer waveguide is employed to guide the emitted radiation from the horn antenna to crystal detector and oscilloscope. TOF diagnostics by using a longer waveguide of about 54.5 cm displays the difference between two experimental approach even more clearly. In these measurements the width of each pulse of the radiation in the gas filled chamber was broaden noticeably about three times, but the pulse width of the radiation from the gas jet plasma doesn't change as shown in Figure 14.

Detected radiation pulses from gas jet (solid line) and static gas filled chamber (dashed line at chamber pressure of 360 Pa and dotted line at 3600 Pa). (a), (b), and (c) refer to wave guide at 4.5, 25.5, and 54.5 cm lengths, respectively.

Broadening of the pulse width of the radiation during the flight through longer waveguide is due to different group velocities that the frequencies contained in the pulse. Thus the results of those measurements indicate that the wide range of the frequency in the radiation from the gas-filled chamber is produced, while the radiation from the gas jet flow is found to be quasi-monochromatic. Difference can be seen that the nonuniform plasma density along the laser propagation in the case of gas-filled chamber, while the gas jet plasma characterizes uniform density, and sharp boundary. In other words, it shows that the effect of gas jet nozzle localize the gas and uniform density and sharp boundary plasma can be generated.

Another effect of using the gas jet plasma to excite the radiation is as follow. Typical radiation waveform observed by using the gas jet flow (Fig. 6) consist of single radiation pulse of millimeter wavelength, whereas the radiation from gas filled chamber obtained in similar experimental conditions represents a set of pulses. Number of these pulses and their relative intensities depend on experimental conditions, namely, on the gas pressure.

4.3. Radiation in the x direction

The ratio of amplitude of longitudinal to transverse component of electrons oscillations due to interaction of laser pulse and plasma on the laser axis is (Marques et al., 1998)

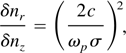
where ωp is the plasma electrons angular frequency and σ is the laser focal spot radius. With the parameter of our experiment the amplitude of transverse oscillation is about four times larger than the longitudinal oscillation.

For the first time a new component of radiation is observed, which propagates in the x direction perpendicular to the direction of laser pulse propagation and magnetic field lines. In Figure 15 a typical radiation waveform is shown obtained from nitrogen plasma at B0 = 7.8 kG corresponds to ωc = 1.4 × 1011 rad/s and neutral gas density is 1.5 × 1017 cm−3. The observed pulse duration of the order of 200 ps at FWHM, is limited by the bandwidth of the receiving equipment.

Sample of the radiation pulse propagates in the X direction.

The polarization of the emitted radiation is measured by rotating the receiver horn antenna around the x axis. Radiation is polarized in the z direction. Data are shown in Figure 16. The signal is detected by a 31.4 GHz cutoff waveguide. The data are normalized to the maximum value at θ = 0 or 180 degree. The polarization angle of 0 or 180 degree corresponds to polarization in the z direction. The solid line indicates the electric field intensity distribution cos2 θ which is the expected value of a tiny dipole antenna located along z axis. With respect to the effective radial component of the ponderomotive force of plasma Wakefield in the x direction (y component is parallel to magnetic field lines), electrons are made to rotate around the magnetic field lines in the x − z plane and generate the electromagnetic component of the Wakefield in the z direction perpendicular to the direction of the applied external dc magnetic field. Experimental data show that polarization of the radiation in the z direction, is in fairly good agreement with expectation.

Intensity of the electric field of emitted radiation versus angle of the horn antenna.

Intensity of the radiation versus applied external dc magnetic field. (a) and (b) are data from gas-filled chamber plasma (a) and gas jet plasma (b), respectively

The spatial distribution of the radiation is measured by changing the position of the horn antenna in different angles refer to the x axis in the x − y plane. The radiation is mainly launched within the angle ±5 degree with respect to the x axis in the x − y plane. Pulse becomes weaker in larger angles up to ±8 degree and absolutely disappear after that. Because of limitations due to experimental set up, it is impossible for us to measure the spatial distribution of the radiation in the z − x plane at the same time.

5. MORE DISCUSSION ON THE RADIATION CHARACTERISTICS

Comparing to radiation from the statistic gas filled chamber experiment (Yugami et al., 2002), the main observed differences are due to generation of the sharp boundary plasma.

Typical radiation waveform observed by using the gas jet flow consist of single radiation pulse of millimeter wavelength, whereas the radiation from gas filled chamber obtained in similar experimental conditions represents a set of pulses. Number of these pulses and their relative intensities depend on experimental conditions, namely, on the gas pressure.

Pulse broadening of the radiation during the flight through the longer waveguide is another effect which occurs noticeably only for radiation from gas-filled chamber plasma. Compare to this, the pulse width of the radiation pulse from the gas jet plasma doesn't broaden noticeably in longer waveguides. Broadening the pulse width of the radiation during the flight through the longer waveguide is due to different group velocities and frequencies in the pulse. Thus the results of those measurements indicate the wide frequency range of the radiation from the gas-filled chamber, whereas radiation from the gas jet flow is found to be quasi-monochromatic. Difference can be because of the nonuniform plasma density in the case of using the gas-filled chamber, while the gas jet plasma characterizes by uniform density and sharp boundary. In other words, it shows the effect of gas jet nozzle in localizing the gas and generating the plasma with uniform density and sharp boundary.

The most important observed difference is the behavior of the radiation intensity with changing the magnetic field as shown in Figure 17. Figures 17a and 17b present the intensity change of the radiation from gas filled chamber (a) and gas jet plasma (b), respectively. In the case of gas jet plasma the output power of the radiation is proportional to ωc2, or B02. Damping effect due to non-sharp boundary phenomenon doesn't affect the radiation but in the case of radiation from gas filled chamber, output power decrease with increasing the magnetic field strength over 5 kG. The effect of non-sharp boundary is taken into account and the result is shown by the solid line in Figure 17a. It is noticeable that Figures 17a and 17b are the same if we focus on the part where power increase with magnetic field. In another word, the dependence on magnetic field is weaker in (a) and stronger in (b), which could be due to the boundary effect. Also in the middle of them one large or two small peaks exist in both cases. The difference occurs in the last part where the attenuation due to non-sharp boundary effect clearly increase the radiation intensity.

All the above mentioned differences clearly confirm the effect of the gas jet to generate the sharp boundary plasma. Due to this effect the attenuation of the output power caused from ramp boundary phenomena can be controlled.

The output power of the radiation is estimated to be about 5 mW, much more smaller than the expected value. Theoretically the amplitude of the electric field of the Wakefield in the plasma is proportional to n1/2 of the order of GeV/m.

Another point is the radiation frequency. The measured frequency by the method of TOF is 57.57 GHz, corresponds to plasma density of 3.5 × 1013 cm−3. Which is about 104 times less than the plasma density of the experiment measured by Mach-Zehender interferometer.

The measured pulse duration of radiation in our experiment is less than 200 ps at FWHM, because 200 ps is the limitation of the bandwidth of the receiving equipment. The life time or damping time of the wakes in the plasma can be estimated from (Yugami et al., 2002)

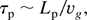
where Lp is the plasma length of the order of Rayleigh length and vg is the group velocity of the wakes in the plasma. In this experiment with laser spot size of 20 μm, Lp is estimated to be about 1.55 mm. The electron density is about 1017 cm−3 correspondingly ωp ≃ 1.8 × 1013 rad/s so τp should be about 80 ns theoretically.

Although the direction of the polarization of radiation and effect of magnetic field in the radiation intensity strongly confirm that the radiation is due to the new electromagnetic component of magnetized plasma Wakefield but the mentioned features of the radiation confirm that the main energy of large amplitude plasma Wakefield at the core of the plasma is still confined in the plasma and dissipated in the form of plasma heating. They do not contribute in the radiation and the observed radiation is from the electrons oscillation of a thin layer at plasma edge near the boundary between plasma and vacuum.

This could be explained by the great difference between the group velocity of Wakefield in the plasma and radiation in the vacuum. At ω ≈ ωp the group velocity of the Wakefield in the plasma is;

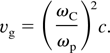
For our experiment we have vg = 0.5 × 10−4c while the velocity of the radiation in the vacuum is c.

From another view, by estimating the plasma length Lp ≈ 1.5 mm and plasma life time less than 200 ps, we can see only that part of the wake, whose group velocity in the axial direction is about 109 cm/s or more are taken part in the radiation, but it is well known that in order to produce Wakefield with larger amplitude we need to focus the beam in a smaller spot so the wake group velocity decreases in the axial direction and increases in the radial direction, which leads to dissipating a part of Wakefield energy in the plasma.

6. CONCLUSION

Short pulse radiation from the interaction of short intense laser pulse and magnetized gas jet plasma is studied as a new source of coherent radiation tunable in frequency pulse duration and intensity. By using gas jet flow to generate the plasma, the effect of the sharp plasma boundary on the radiation intensity is investigated and differences between radiation from gas-filled chamber and gas-jet plasma is reported. Radiation due to radial component of Wakefield is investigated and characteristics of this radiation is introduced. Some features of the radiation confirm that the main energy of large amplitude plasma Wakefield at the core of the plasma is still confined in the plasma and do not contribute in the radiation.

ACKNOWLEDGMENTS

We would like to acknowledge Professor Michael I. Bakunov with Department of Radiophysics, University of Nizhny Novgorod, Russia for his very useful discussions and Dr. Higashiguchi with Department of Electrical and Electronic Engineering, Miyazaki University of Japan for his useful technical supports. We also are grateful to Cooperative Research Center and Satellite Venture Business Laboratory (SVBL) of Utsunomiya University for providing us the laser system. A part of the work is supported by the Grant-in-Aid in Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology, Japan.

References

REFERENCES

Bakunov, M.I., Bodrov, S.B., Dorranian, D., Yugami, N. & Nishida, Y. (2003). 2D theory of THz radiation from magnetized plasma wakes. Proceeding of the 28th International Conference On Infrared And Millimeter Waves. Otsu, Japan, 1, 363.
Baton, S.D., Amiranoff, F., Malka, V., Modena, A., Salvati, M., Coulaud, C., Rousseaux, C., Renard, N., Mounaix, P. & Stenz, C. (1998). Measurement of a spatially smoothed laser beam in homogenous large scale plasma. Phys. Rev. E 57, 4895–4898.Google Scholar
Coverdale, C.A., Darrow, C.B., Decker, C.D., Mori, W.B., Tzeng, K.C., Marsh, K.A., Clyton, C.E. & Joshi, C. (1995). Propagation of intense subpicosecond laser pulses through under dense plasmas. Phys. Rev. Lett. 74, 4659–4662.Google Scholar
Denavit, J. & Phillion, D.W. (1994). Laser ionization and heating of gas targets for longscale-length instability experiments. Phys. Plasmas 1, 1971–1984.Google Scholar
Dodin, I.Y. & Fisch, N.J. (2002). Storing retrieving and processing optical information by Raman back scattering in plasma. Phys. Rev. Lett. 88, 165001.Google Scholar
Dorranian, D., Ghoranneviss, M., Starodubtsev, M., Ito, H., Yugami, N. & Nishida,Y. (2004). Generation of short pulse radiation from magnetized wake in gas-jet plasma and laser interaction. Phys. Lett. A 331, 77–83.Google Scholar
Dorranian, D., Starodubtsev, M., Kawakami, H., Ito, H., Yugami, N. & Nishida, Y. (2003). Radiation from high-intensity ultrashort laser pulse and gas-jet magnetized plasma interaction. Phys. Rev. E 68, 026409.Google Scholar
Fiedorowics, H., Bartnik, A., Patron, Z. & Parys, P. (1994). X-ray emission from laser irradiated gas puff targets. Appl. Phys. Lett. 62, 2778–2780.Google Scholar
Fill, E., Borgstrom, S., Larson, J., Starczewski, T. & Svanberg, C.G. (1995). Xuv spectra of optical field ionized Plasmas. Phys. Rev. E 51, 6016–6027.Google Scholar
Ginzburg, V.L. (1970). The Propagation of Electromagnetic Waves in Plasmas. New York: Pergamon Press.
Gushenets, V.I., Oks, E.M., Yushkov, G.Y.U. & Rempe, N.G. (2003). Current status of plasma emission electronics: I. Basic physical processes. Laser Part. Beams 21, 123–138.Google Scholar
Hagena, O.F. & Obert, W. (1972). Cluster formation in expanding supersonic jets: Effect of pressure, temperature, nozzle size, and test Gas. J. Chem. Phys. 56, 1793–1802.Google Scholar
Hamster, H., Sullivan, A., Gordon, S., White, W. & Falcon, R.W. (1993). Sub picosecond electromagnetic pulses from intense laser-plasma interaction. Phys. Rev. Lett. 71, 2725–2728.Google Scholar
Hora, H. (2004). Development in inertial fusion energy and beam fusion at magnetic confinement. Laser Part. Beams 22, 439–449.Google Scholar
Hora, H., Osman, F., Castillo, R., Collins, M., Stait-Gardener, T., Chan, W., Holss, M., Scheid,W.,Wang, J.X. & Yu-Kun, H. (2002). Laser-generated pair production. Laser Part. Beams 20, 79–86.Google Scholar
Ji, P. (2001). Photon acceleration based on plasma. Phys. Rev. E 64, 036501.Google Scholar
Katsouleas, T. & Bingham, R. (Eds.) (1996). Special issue on second generation plasma accelerators. IEEE. Trans. Plasma Sci. 24.Google Scholar
Korovin, S.D., Kurkan, I.K., Loginov, S.V., Pegal, I.V., Polevin, S.,D., Volkov, S.N. & Zherlitsyn, A.A. (2003). Decimeter-band frequency-tunable sources of high-power microwave pulses. Laser Part. Beams 21, 175–185.Google Scholar
Li, Y.M. & Fedosejevs, R. (1994). Density measurements of a high-density pulsed gas jet for laser-plasma interaction studies. Meas. Sci. Technol. 5, 1197–1201.Google Scholar
Lin, H., Chen, L.M. & kieffer, J.C. (2002). Harmonic generation of ultra-intense laser pulses in under dense plasma. Phys. Rev. E 65, 036414.Google Scholar
Malka, V., Coulaud, C., Geindre, J.P., Lopez, V., Najmudin, Z., Neely, D. & Amiranoff, F. (2000). Characterization of neutral density profile in a wide range of pressure of cylindrical pulsed gas jets. Rev. Sci. Instrum. 71, 2329–2333.Google Scholar
Marques, J.R., Dorchies, F., Amiranoff, F., Audebert, P., Gauthier, J.C. & Geindre, J.P. (1998). Laser Wakefield: Experimental study of nonlinear radial electron oscillation. Phys. Plasmas 5, 1162–1177.Google Scholar
Mesyats, G.A. (2003). Guest Editors Foreword: Special issue on the occasion of the 25th anniversary of the Institute of High Current Electronics of the Russian Academy of Sciences, Siberian Division, and references therein. Laser Part. Beams 21, 121.Google Scholar
Modena, A., Najmudin, Z., Dangor, A.E., Clyton, C.E., Marsh, K.A., Joshi, C., Malka, V., Darrow, C.B., Danson, C., Nely, D. & Walsh, F.N. (1995). Electron acceleration from the breaking of relativistic plasma waves. Nature 377, 606–608.Google Scholar
Muggli, P., Guang, C., Oz, E., Narang, R., Filip, C.V., Tochitsky, S., Clyton, C.E., Marsh, K.A., Mori, W.B., Joshi, C., Yoder, R.B., Rosenzweig, J. & Katsouleas, T. (2002). THz Cerenkov radiation from a magnetized plasma. 29th IEEE International Conference on Plasma Science, Banff, Alberta, Canada.
Osman, F., Cang, Y., Hora, H., Cao, L., Liu, H., Badziak, J., Parys, A.B., Wolowski, J., Woryna, E., Jungwirth, K., Kralikova, B., Krasa, J., Laska, L., Pfeifer, M., Rohlena, K., Skala, J. & Ullschmied, J. (2004). Skin depth plasma front interaction mechanism with prepulse suppression to avoid relativistic self-focusing for high-gain laser fusion. Laser Part. Beams 22, 83–87.Google Scholar
Wilcox, D.C. (2000). Basic Fluid Mechanics, 2nd ed. La Canada, CA: DCW Industries Inc.
Yoshii, J., Lai, C.H., Katsouleas, T., Joshi, C. & Mori, W.B. (1997). Radiation from Cerenkov wakes in a magnetized plasma. Phys.Rev. Lett. 79, 4194–4197.Google Scholar
Yugami, N., Higashiguchi, T., Gao, H., Sakaii, S., Takahashi, K., Ito, H., Nishida, Y. & Katsouleas, T. (2002). Experimental observation of radiation from Cherenkev wakes in a magnetized plasma. Phys. Rev. Lett. 89, 065003.Google Scholar
Figure 0

Schematic view of EM radiation generation.

Figure 1

Angular distribution of the radiation.

Figure 2

Dispersion relation of the magnetized plasma. Evanescent regions are shown by dashed area.

Figure 3

Interferometer fringe shift of different nozzles are shown at the top. Diamonds on dashed dotted line, squares on dotted lines and circles on dashed line are the neutral gas density magnitudes at different back pressures of nozzles (a), (b), and (c) correspondingly.

Figure 4

Experimental setup.

Figure 5

Sample of the radiation pulse. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

Figure 6

Radiation intensity versus the rotation angle of the horn antenna around z direction. Radiation is polarized the x direction. Filled dots are experimental data and dashed line is expectation from the theory. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

Figure 7

Spatial distribution of the emitted radiation. B0 = 7.8 kG and n0 = 1 × 1017 cm−3.

Figure 8

Radiation intensity in relative units versus neutral gas density for both He (dotted full square line) and N2 (dashed full circle line) plasma The experiment is done by nozzle (a). B0 ≅ 8 kG.

Figure 9

Radiation intensity of three different nozzles at constant gas pressure of 15 MTorr of N0·B0 = 8 kG.

Figure 10

Output power of the radiation as a function of the applied external dc magnetic field. Solid line indicates the theoretical values (≈B02). Error bars show the difference between the maximum and minimum of the obtained experimental data.

Figure 11

Scheme of TOC experiment setup.

Figure 12

Detected pulses at points (a), (b), (c), and (d) of the waveguide. Delay times are referred to point (a).

Figure 13

Detected radiation pulses from gas jet (solid line) and static gas filled chamber (dashed line at chamber pressure of 360 Pa and dotted line at 3600 Pa). (a), (b), and (c) refer to wave guide at 4.5, 25.5, and 54.5 cm lengths, respectively.

Figure 14

Sample of the radiation pulse propagates in the X direction.

Figure 15

Intensity of the electric field of emitted radiation versus angle of the horn antenna.

Figure 16

Intensity of the radiation versus applied external dc magnetic field. (a) and (b) are data from gas-filled chamber plasma (a) and gas jet plasma (b), respectively