1. INTRODUCTION
The recently reoriented US heavy ion program (Logan et al., 2005) advocates the production of warm dense matter (WDM) with intense ion beams partially stopped in thin foil, in the vicinity of the Bragg peak (Grisham, 2004). The idea is to warm up as uniformly as possible target foils exposed to intense heavy ion beams that have been linearly accelerated. More precisely, it is planned to use moderate energy ions (∼0.3–3 MeV/a.m.u) as low cost drivers for high energy density physics (HEDP) experiments. Target thickness could then be selected, so the ion beam enters and then leaves the target in close vicinity of the dE/dx peak, so that d2E/dx2 ≅ 0. As a result, high uniformity of energy deposition can be expected with a maximum of energy per beam particle deposited in target (Grisham, 2004).
The formal presentation of this program (Logan et al., 2005) details high-current ion sources injection, transport, final focussing, chambers and targets for HEDP, and inertial fusion energy (IFE), driven by the induction of linac accelerators. In order to optimize WDM production, this program addressed the physics of neutralized beam compression and focusing to the high intensities requested for efficient target heating (Ng et al., 2005).
Despite several very recent and thorough presentations, this conspicuous program does not pay much attention to the energy loss mechanisms actually at stake in the interaction processes underlying WDM production. It is for this reason that we intend to review and formalize to a certain extent, the basic physics of intermediate and low velocity ion stopping. As well documented (Deutsch, 1986; Deutsch et al., 1989; Hoffmann et al., 1990; Deutsch & Maynard, 2000), the given stopping power is no longer ∼Vp−2, with Vp denoting the ion projectile velocity, but rather ∼Vp, where Vb << Vthe is the target electron thermal velocity. We intend to emphasize that the Bragg peak should be treated as an intermediate (or low Vb ∼ Vthe) or low Vp energy loss. Fortunately, the US proposal is concomitant with many theoretical and numeral studies devoted to low Vp stopping, mostly in cold matter. Therefore, we review the given proposed results in connection with the US program.
Section 2 revisits the intermediate and low velocity (ILV) regime when target electrons stop ion beams with Vb < Vthe while Vp remains significantly larger than Vthi thermal ion velocity in target. Such a situation is already well documented through thermonuclear alpha heating of fusion plasmas (Goldston & Rutherford, 1995).
In Section 3, we stress the operational significance of ion energy loss near Vp = 0, and for an arbitrary coupling between projectile charge Zp and target electrons, in a weakly coupled target plasma with Γe = e2/kBTa < 1 and a = (4/3πne)−1/3 with Z = target ion charge, ne denoting the target electron number density. It should also be appreciated that a few eV electron fluids can remain mostly non-degenerate with Γe ∼ 1.
Section 4 highlights the progress of a highly charged and low velocity ion beam through dense plasma before recombination with conveyed target electrons takes place. Prospective remarks are presented in Section 5.
2. ILV ION STOPPING IN ELECTRON-ION TARGET PLASMA
Now, we detail the above advocated ILV regime. First, we make the proviso that intra-beam ion-ion correlations can be safely neglected in dense plasma targets. Otherwise stated, the given mean ion distance is likely to remain orders of magnitude above target electron screening length (Debye at Te >> TF, or Thomas-Fermi ≤ TF). This assumption is very close to the “dilute beam in target” assumption, commonly used for heavy ion beam (HIB) driven IFE (Deutsch, 1986).
The basic interaction scheme underlying the recently proposed US program (Grisham, 2004; Logan et al., 2005) is vividly pictured on Figure 1.

Warm dense matter (WDM) production at Bragg peak (Logan et al., 2005).
It is also implied that under intense ion beams irradiation, thin target foil will be very rapidly heated to a hot plasma state. In such a situation, ILV mechanisms underlying Bragg peak energy loss are expected to rely on a Vb < Vthe and Vb > Vthi regime. In a Γ < 1, target plasmas, stopping quantities are likely to be linearly dependent on the electron Coulomb logarithm [ell ]nΛ, with

where nD denotes the number of electrons in a Debye sphere, with Te = Ti in the target.
Then ion stopping at moderate velocities with Vthi << Vb << Vthe in a target plasma assumed to be composed of Maxwellian ions and electrons, for ion beam (Mb, Zb, Eb) and target ions (M,Z) can be expressed (Goldston & Rutherford, 1995) for Vb << Vthe as
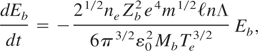
m = electron mass, and

for Vb >> Vthi. Altogether one gets
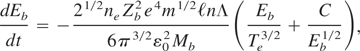
where
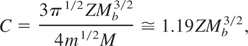
for Mb arbitrary and M ≅ 48 (titanium), in m unit. Critical Eb,crit fulfilling
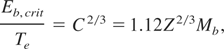
denotes a crossover between a situation mostly controlled by electron stopping (Eb > Eb,crit) while (Eb < Eb,crit) pertains to stopping mostly arising from target ions.
Let us recall that dE/dx = Vb−1 × dE/dt, and that in context of producing WDM with Ti (titanium) targets, one should expect Z = 1, 2 (1 or 2 eV target temperature). WDM with quasi-classical electrons may be obtained from Cs targets at a few eV, in view of its very Fermi temperature TF ∼ 1.7 eV and C = 0.43 ZMb2/3.
Neglecting multiple scattering effects on target ions, one can ignore velocity diffusion coefficient compared to dynamical friction featured as ion beam losses on target electron and ion. This amounts to a Fokker-Planck description,
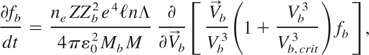
where
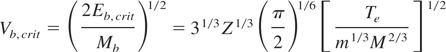
for the ion beam distribution, with a critical velocity Vb,crit Mb-independent. Again for a Ti target (M = 48), Eq. (8) specifies to

3. ZERO VELOCITY ION STOPPING
Concentrating now on the most significant ion stopping arising from target electrons, we pay attention to
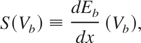
near Vb = 0. The ratio S(Vb)/Vb usually monitors a linear stopping profile, up to 100 keV/a.m.u (Paul & Schinner, 2003) in cold matter. Similar trends are also reported in highly ionized plasma (Deutsch, 1986; Deutsch & Maynard, 2000).
From now on, we intend to make use of a very powerful connection between very low velocity ion stopping and particle diffusion (Dufty et al., 2004; Talin et al., 2003; Forster, 1975) through Einstein characterization of ion mobility associated to thermal electron fluctuations in target, around the slow ion projectile visualized as an impurity immersed in a dense and homogeneous electron fluid. The given relationship thus reads as
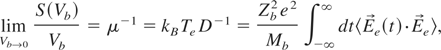
in terms of a Green-Kuho integrand (Forster, 1975) involving electric field fluctuations from the target electrons.

qualifies as the total electric field at impurity due to surrounding electrons.
A fundamental restriction on the relations (10) arises from the strong inequality Mp /m >>> 1, between projectile and electron mass. The integrand on the right-hand side in Eq. (10) is illustrated on Figure 2, which contrasts molecular-dynamics (MD) simulations to an analytic model using a short range regularized Coulomb effective interaction between “impurity” Zb and target electrons (Deutsch, 1977), given as

where δ = (2πħ2/2me kbTe)1/2 refers to target electron thermal De Broglie wavelength. In Figure 2, C(t) refers to the dimensionless expression
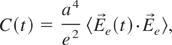
in terms of mean inter-electron distance a.

Comparison of C(t) from MD and from equation for Zb = 8 and 30 at Γ = 0.1 and δ = 0.4 (From Dufty et al., 2003).
It should be appreciated that Zb high values lead to an anti-correlation (C(t) < 0) for 0.25 < ωp < 1, ωp denoting target electron plasma frequency. This feature highlights an arbitrarily strong coupling between low velocity ion projectile and target electrons. This coupling may be expressed by Eq. (11)

Contrasting again in Figure 3, MD simulation results with analytic ones, both are based on Eq. (11). One can witness a nearly parabolic rise of S(Vb)/Vb in terms of coupling σ. It would be highly desirable to extend such investigations to any Γe values.

Stopping power vs coupling for moderate coupling conditions (From Dufty et al., 2004).
4. LOW VELOCITY PROJECTILE IN DENSE PLASMA
In the present context, it appears useful to make contact with numerical simulations tracking the low velocity ion projectile in the dense target plasma. Rather instructive ones are just been offered by a group from the Tokyo Institute of Technology (Oguri et al., 2005).
These authors have thus numerically investigated the stopping power of low-energy, highly charged projectiles in cold dense plasmas in order to determine realistic parameters for beam-plasma interaction experiments with low energy (10–100 keV/a.m.u) ion projectiles delivered by a 1.7 MV electrostatic accelerator. They used a simple MD computer code and observed that for projectile velocity as low as thermal electron velocity, in a sufficiently high charge state, non linear stopping as advocated above can be witnessed even for a weakly coupled plasma target with Γe ≅ 0.1 (see Fig. 4).

Framing images of plasma electrons and electron density distributions along the z-axis for three different projectile positions. The outer frames show the wall of the box. A 20 keV/u93Nb40+ projectile was injected into the plasma from the left side at x = y = z = 0. The arrows show the longitudinal positions of the projectile. The electron density and temperature of the target plasma are 1021 cm−3 and 10 eV, respectively. The axial electron density distribution was calculated for a paraxial region of −1 nm < x < 1 nm and −1 nm < y < 1 nm (From Oguri et al., 2005).
It should be noticed that projectiles with such high charge state rapidly disappear through a strong recombination with target electrons conveying the ion projectile, even in the absence of residual hydrogen atoms in the plasma. These can prove very efficient in transferring their bound electrons to the incoming ion, even at very high dilution.
5. PROSPECTIVE REMARKS
This rather sketchy presentation of the US beam-target program, highlights its content in rejuvenated questioning for the field of ion stopping in matter. Among the most urgent and challenging inquiries, let us retain:
- Projectile effective charge near end of range
- Inflight projectile spectroscopy
- Strong Coulomb correlations in target → WDM
- Ion multiple scattering and straggling
- Superelastic contribution to low Vb ion stopping
- Validation of global sum rule for arbitrary ion beam distribution
- Projectile excitation (Z projectile > Z target).
ACKNOWLEDGMENT
We thank deeply Gilles Maynard for a careful reading of the manuscript.






