Introduction
Over the past 20 years, various laboratories have been actively studying the interaction of a nanosecond laser pulse of terawatt power with a substance that has an internal stochastic or regular structure in the form of solid elements, typically membranes or filaments, separated by vacuum gaps, as in porous plastics ([CH]n, [CH2]n), agar-agar (C12H18O9), threeatsetat-cellulosa (C12H16O8), trimethylolpropane triacrylate (C15H20O6), and polyvinylalcohol ([CH2CH(OH)]n). Due to its low density and heterogeneous structure, such a substance can be used as the constituent of a direct-driven Laser Thermonuclear Fusion (LTF) target for effective volume absorption of the laser radiation (Gus'kov et al., Reference Gus'kov, Zmitrenko and Rozanov1995, Reference Gus'kov, Caruso, Rozanov and Strangio2000a; Bugrov et al., Reference Bugrov, Gus'kov, Rozanov, Burdonskii, Gavrilov, Gol'tsov, Zhuzhukalo, Koval'skii, Pergament and Petryakov1997; Gus'kov & Rozanov, Reference Gus'kov and Rozanov1997), providing a high absorption efficiency exceeding 80% for a Nd-laser radiation, as registered in experiments (Bugrov et al., Reference Bugrov, Gus'kov, Rozanov, Burdonskii, Gavrilov, Gol'tsov, Zhuzhukalo, Koval'skii, Pergament and Petryakov1997, Reference Bugrov, Burdonskii, Gavrilov, Gol'tsov, Gus'kov, Koval'skii, Kondrashov, Medovshchikov, Pergament, Petryakov, Rosanov and Zhuzhukalo1999; Caruso et al., Reference Caruso, Strangio, Gus'kov and Rozanov2000; Gus'kov et al., Reference Gus'kov, Caruso, Rozanov and Strangio2000a). Moreover, it can be employed to smooth the inhomogeneities in the distribution of absorbed laser energy (Desselberger et al., Reference Desselberger, Jones, Edwards, Dunne and Willi1995; Dunne et al., Reference Dunne, Borghesi, Iwase, Jones, Taylor, Willi, Gibson, Goldman, Mack and Watt1995; Gus'kov et al., Reference Gus'kov, Zmitrenko and Rozanov1995, Reference Gus'kov, Caruso, Rozanov and Strangio2000a, Reference Gus'kov, Gromov, Merkul'ev, Rozanov, Nikishin, Tishkin, Zmitrenko, Gavrilov, Gol'tsov, Kondrashov, Kovalsky, Pergament, Garanin, Kirillov, Sukharev, Caruso and Strangiob; Koch et al., Reference Koch, Estabrook, Bauer and Back1995; Kalantar et al., Reference Kalantar, Key, DaSilva, Glendinning, Knauer, Remington, Weber and Weber1996; Bugrov et al., Reference Bugrov, Gus'kov, Rozanov, Burdonskii, Gavrilov, Gol'tsov, Zhuzhukalo, Koval'skii, Pergament and Petryakov1997; Gus'kov & Rozanov, Reference Gus'kov and Rozanov1997; Watt et al., Reference Watt, Wilson, Chrien, Hollis, Gobby, Mason and Kopp1997, Reference Watt, Duke, Fontes, Gobby, Hollis, Kopp, Mason, Wilson, Verdon, Boehly, Knauer, Meyerhofer, Smalyuk, Town, Iwase and Willi1998; Batani et al., Reference Batani, Nazarov, Hall, Löwer, Koenig, Faral, Benuzzi-Mounaix and Grandjouan2000; Nishimura et al., Reference Nishimura, Shiraga, Azechi, Miyanaga, Nakai, Izumi, Nishikino, Heya, Fujita, Ochi, Shigemori, Ohnishi, Murakami, Nishihara, Ishizaki, Takabe, Nagai, Norimatsu, Nakatsuka, Yamanaka, Nakai, Yamanaka and Mima2000; Hall et al., Reference Hall, Batan, Nazarov, Koenig and Benuzzi2002) and also to increase the degree of conversion of laser radiation into X ray (Shang et al., Reference Shang, Yu, Zhang and Yang2016; Chaurasia et al., Reference Chaurasia, Kaur, Borisenko, Pasley, Orekhov and Deo2017), in the context of indirect target drive scheme (Xu et al., Reference Xu, Zhu, Li and Yang2011; Thomas, Reference Thomas2017) or for powerful laser sources of neutron and X-ray radiation (Gus'kov et al., Reference Gus'kov, Zmitrenko and Rozanov1997). The doping of a porous material with heavy chemical elements can improve the conversion of laser radiation into X rays, useful for direct target irradiation by X rays without the use of the hohlraum (Gus'kov & Merkul'ev, Reference Gus'kov and Merkul'ev2001) as well as for the development of effective radiography methods (Fournier et al., Reference Fournier, May, Colvin, Kane, Schneider, Dewald, Thomas, Compton, Marrs, Moody, Bond, Michel, Fisher, Newlander and Davis2010; Pérez et al., Reference Pérez, Patterson, May, Colvin, Biener, Wittstock, Kucheyev, Charnvanichborikarn, Satcher, Gammon, Poco, Fujioka, Zhang, Ishihara, Tanaka, Ikenouchi, Nishimura and Fournier2014).
Modeling the porous substance as a continuous homogeneous medium with fixed specific properties for laser light absorption and energy transfer (Gus'kov et al., Reference Gus'kov, Demchenko, Rozanov, Stepanov, Zmitrenko, Caruso and Strangio2003; Lebo & Lebo, Reference Lebo and Lebo2009; Rozanov et al., Reference Rozanov, Barishpolt'sev, Vergunova, Demchenko, Ivanov, Aristova, Zmitrenko, Limpouch and Ulschmidt2016) allows to obtain integral characteristics of energy transfer for a given type of porous substance and given experimental conditions, but the foam properties do not evolve during the calculation. Recently, simulations have been performed with the two-dimensional hydrodynamic code PALE (Velechovsky et al., Reference Velechovsky, Limpouch, Liska and Tikhonchuk2016), by implementing a two-scale model for laser light absorption and limiting electron conductivity depending on the homogenization degree of the plasma. Despite the quantitative agreement with the data of all known experiments with subcritical foams where ionization wave velocity was measured (Limpouch et al., Reference Limpouch, Demchenko, Gus'kov, Kálal, Kasperczuk, Kondrashov, Krouský, Mašek, Pisarczyk, Pisarczyk and Rozanov2004; Borisenko et al., Reference Borisenko, Akimova, Gromov, Khalenkov, Merkuliev, Kondrashov, Limpouch, Kuba, Krousky, Masek, Nazarov and Pimenov2006; Khalenkov et al., Reference Khalenkov, Borisenko, Kondrashov, Merkuliev, Limpouch and Pimenov2006; Depierreux et al., Reference Depierreux, Labaune, Michel, Stenz, Nicolai, Grech, Riazuelo, Weber, Riconda, Tikhonchuk, Loiseau, Borisenko, Nazarov, Huller, Pesme, Casanova, Limpouch, Meyer, Di-Nicola, Wrobel, Alozy, Romary, Thiell, Soullie, Reverdin and Villette2009; Nicolai et al., Reference Nicolai, Olazabal-Loumé, Fujioka, Sunahara, Borisenko, Gus'kov, Orekov, Grech, Riazuelo, Labaune, Velechowski and Tikhonchuk2012), the code is limited to simulate only subcritical foams with a closed pore structure.
This work is the further development of Gus'kov et al. (Reference Gus'kov, Cipriani, De Angelis, Consoli, Rupasov, Andreoli, Cristofari and Di Giorgio2015), where we developed a model in which the absorption efficiency depends on the foam characteristics, which vary in space and time following the degree of homogenization. In this work, we explain the implementation of the model in the new MULTI-FM code and the results of the most relevant simulations. MULTI-FM is a modification of the well-known MULTI code (Ramis et al., Reference Ramis, Schmaltz and Meyer-ter-Vehn1988) with the inclusion of macroscopic models of absorption of laser radiation and energy transfer in porous media. It allows simulating the behavior of porous media with large and small pores of average density larger or smaller than the critical plasma density, irradiated by nanosecond laser pulses in the parameter range of the major facilities for inertial confinement fusion studies. The code can contribute to the better design of targets and experiments, thanks to its predictions on hydrothermal wave speed, absorption efficiency, and pressure buildup, more reliably than usual hydrodynamic simulations with homogeneous targets.
Physical phenomena
The key phenomenon of laser-driven plasma creation in the foam is the viscous homogenization in the heated region of matter (Gus'kov et al., Reference Gus'kov, Gromov, Merkul'ev, Rozanov, Nikishin, Tishkin, Zmitrenko, Gavrilov, Gol'tsov, Kondrashov, Kovalsky, Pergament, Garanin, Kirillov, Sukharev, Caruso and Strangio2000b). The structure of a porous substance is determined by the fractal parameter α in the form (Guskov, Reference Gus'kov2010)
where δ0 and b 0 are, respectively, the average pore size and solid element thickness; ρs and ρp are, respectively, the initial density of solid elements and the average density of the foam. The parameter α depends on the form of solid elements and is approximately equal to (ν + 1)−1, where the values ν = 0, 1, 2 correspond to its planar (membrane), cylindrical (filament), or spherical (cluster) form. For the membrane-filamentary structure mentioned in the introduction, which characterizes most of the light foams, the value α = 0.8 provides the best agreement of theoretical estimates with the experimental data, especially for the homogenization rate (Gus'kov et al., Reference Gus'kov, Limpouch, Nicolai and Tikhonchuk2011).
The absorption coefficient derived in (Gus'kov et al., Reference Gus'kov, Cipriani, De Angelis, Consoli, Rupasov, Andreoli, Cristofari and Di Giorgio2015) is:
 $$\eqalign{& K_{\rm f}(x,t) = \displaystyle{{{\rm \delta} _0} \over {b_0L_{{\rm p}0}}}\left\{ {\displaystyle{1 \over {(1 - (b_0/{\rm \delta} _0)){[1 - H(x,t)]}^{1/2}}} - 1} \right\}, \cr & \quad 0 \le t \le t_h}$$
$$\eqalign{& K_{\rm f}(x,t) = \displaystyle{{{\rm \delta} _0} \over {b_0L_{{\rm p}0}}}\left\{ {\displaystyle{1 \over {(1 - (b_0/{\rm \delta} _0)){[1 - H(x,t)]}^{1/2}}} - 1} \right\}, \cr & \quad 0 \le t \le t_h}$$In this expression, the initial transparency length is expressed as:
and the function H(x,t) characterizes the degree of homogenization increasing with time:
τ0 is the characteristic time of homogenization, which is determined by the ion–ion collision time
 $${\rm \tau} _0 \approx 2.4 \cdot 10^{ - 3}\displaystyle{{Z^4{({\rm \delta} _0 - b_0)}^2{\rm \rho} _{\rm p}} \over {A^{{\textstyle{1 \over 2}}}T^{{\textstyle{5 \over 2}}}}} \approx 2.4 \cdot 10^{ - 3}\displaystyle{{Z^4{\rm \delta} _0^2 {\rm \rho} _{\rm p}} \over {A^{{\textstyle{1 \over 2}}}T^{{\textstyle{5 \over 2}}}}},\quad s$$
$${\rm \tau} _0 \approx 2.4 \cdot 10^{ - 3}\displaystyle{{Z^4{({\rm \delta} _0 - b_0)}^2{\rm \rho} _{\rm p}} \over {A^{{\textstyle{1 \over 2}}}T^{{\textstyle{5 \over 2}}}}} \approx 2.4 \cdot 10^{ - 3}\displaystyle{{Z^4{\rm \delta} _0^2 {\rm \rho} _{\rm p}} \over {A^{{\textstyle{1 \over 2}}}T^{{\textstyle{5 \over 2}}}}},\quad s$$T is plasma temperature; A and Z are the atomic weight and charge of plasma ions, respectively.
At the homogenization time, the degree of homogenization is:
 $$H(x,t_{\rm h}) = H_c = \left\{ {\matrix{ {1\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; {\rm \rho} _{\rm p} \ge {\rm \rho} _{{\rm cr}}} \cr {1 - {\left[ {\displaystyle{{1 - {({\rm \rho} _{\rm p}/{\rm \rho} _{{\rm cr}})}^{\rm \alpha}} \over {1 - {({\rm \rho} _{\rm p}/{\rm \rho} _{\rm s})}^{\rm \alpha}}}} \right]}^2\; \; \; \; \; \; \; {\rm \rho} _{\rm p} \le {\rm \rho} _{{\rm cr}}} \cr}} \right.$$
$$H(x,t_{\rm h}) = H_c = \left\{ {\matrix{ {1\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; {\rm \rho} _{\rm p} \ge {\rm \rho} _{{\rm cr}}} \cr {1 - {\left[ {\displaystyle{{1 - {({\rm \rho} _{\rm p}/{\rm \rho} _{{\rm cr}})}^{\rm \alpha}} \over {1 - {({\rm \rho} _{\rm p}/{\rm \rho} _{\rm s})}^{\rm \alpha}}}} \right]}^2\; \; \; \; \; \; \; {\rm \rho} _{\rm p} \le {\rm \rho} _{{\rm cr}}} \cr}} \right.$$These values are due to the different criterion for defining the plasma to be homogeneous in the two cases. In overcritical foams, the plasma is considered to be homogeneous when the degree of homogenization is equal to 1, meaning that there are no more spatial density variations and that the plasma is opaque to the laser light. In the case of subcritical foams, the plasma is homogeneous when the maximum of the spatial density variations is lower than the critical density, resulting in the value of the homogenization degree in (5).
Because of the partial lack of free electrons in the filling pores, the homogenization process affects the velocity of the ionization wave in the subcritical foam and the velocity of the electron conductivity wave in both subcritical and overcritical foams. In fact, the speed of both these energy transfer processes is limited by the speed of propagation of the homogenization wave. Due to the explosive nature of the expansion of the pore filling, the scale of homogenization wave speed is the sound speed. As a result, the energy transfer wave velocity is significantly lower than the laser-supported ionization wave or the electron conductivity wave velocities in an equivalent subcritical or overcritical homogeneous medium (having the same average density), respectively. Measurements of the ionization wave velocity in the subcritical foams and the velocity of energy transfer wave in the overcritical foams, which prove the fact that these velocities were limited to the sound speed, were experimentally performed. The wave of energy transfer in a foam was named hydrothermal wave (Bugrov et al., Reference Bugrov, Gus'kov, Rozanov, Burdonskii, Gavrilov, Gol'tsov, Zhuzhukalo, Koval'skii, Pergament and Petryakov1997) and the temperature distribution behind its front is uniform due to rapid equalization by electron thermal conductivity. Behind the hydrothermal wave front, part of the energy is contained in the energy of stochastically colliding plasma flows, so that the degree of homogenization determines the magnitude of the pressure gradient. For this reason, it can be concluded that the hydrothermal wave in the early stage of homogenization is an acoustic or weak shock wave, and only at a considerable degree of homogenization it can be transformed into a strong shock wave with a sharp front of the compression region.
Numerical simulation results
Numerical simulations of this work are performed using the one-dimensional hydrodynamic code MULTI-FM where the models of absorption, motion, and electron thermal conductivity of a porous substance of arbitrary density are implemented. In the MULTI-FM code, the degree of homogenization, governing all the relevant properties of the foam plasma, is determined in each numerical cell by the parameter
in which H(x,t) and H c are determined by expressions (4) and (5). The parameter IsFoam is equal to 1 for the cells not yet reached by the laser (cold material) and continuously varies according to the homogenization degree of the cell down to the value 0, at which the plasma is completely homogeneous. To realize the expected smooth transition from foam-like to inverse bremsstrahlung absorption in the inhomogeneous plasma, the total absorption coefficient is calculated, as a first approximation, by the formula:
 $$\eqalign{& K(x,t) \cr & = \sqrt {{\left( {K_f\,(x,t) \cdot {\rm IsFoam}(x,t)} \right)}^2 + {\left( {K_b(x,t) \cdot (1 - {\rm IsFoam}(x,t))} \right)}^2}} $$
$$\eqalign{& K(x,t) \cr & = \sqrt {{\left( {K_f\,(x,t) \cdot {\rm IsFoam}(x,t)} \right)}^2 + {\left( {K_b(x,t) \cdot (1 - {\rm IsFoam}(x,t))} \right)}^2}} $$where K f(x, t) is the absorption coefficient of Eq. (2), while K b(x, t) is the inverse bremsstrahlung absorption coefficient. The IsFoam parameter is evaluated in the beginning of the calculation for the current time step in the code, along with the absorption coefficient, using the values of the parameters from the previous time step. To reproduce the limitation of pressure action and electron conductivity, we introduce the parameter η(x, t) = 1 − IsFoam(x, t) in the momentum and in the heat equations as:
where v(x, t) is the velocity of the plasma, m is the Lagrangian mass coordinate, and P(x, t) is the pressure; q(x, t) is the heat flux, χ(x, t) is the Spitzer conductivity, and T e(x, t) is the electron temperature. This parameterization allows changing the energy transport and mechanical properties of the homogenizing plasma in accordance with its homogenization degree.
The results of simulations in different regimes are reported and discussed in detail, in order to provide an in-depth analysis of the laser-produced plasma properties in foam materials. The solid parts density is of 1 mg/cm3 and average density is equal to 10 mg/cm3. The laser wavelength has been varied to change the critical density without changing the target density, namely from λover = 1054 nm for overcritical foam cases to λsub = 351 nm for subcritical foams. In the simulations of the following sections, the laser intensity has been chosen as I L = 1014 W/cm2 and the value of the fractal parameter was chosen to be α = 4/5, corresponding to the typical membrane-filamentary structured foams used in the recent experiments. The target is taken very thick, namely 2 mm for large-pore foams and 200 µm for small-pore foams, in order to have room for all the thermal and hydrodynamic waves to develop completely in the time of the simulation. All results are compared with ones for a homogeneous substance with the same average density. We initially present the results of simulations where hydrodynamics and electron thermal conductivity are initially switched on separately, to decouple their effect on the homogenization wave. Such details of simulations are shown only for larger pore overcritical foam, where the effect is more evident.
Large-pore foams of overcritical density
In these simulations, the pore size is taken δ0 = 40 μm, corresponding to a solid part thickness b 0 = 1 µm (see, (1)). The initial geometric transparency length results to be L 0 = 492 µm [see (3)]. The conditions of simulations correspond to the experiments on Nd-laser of the ABC installation of the ENEA Frascati Research Center (De Angelis et al., Reference De Angelis, Consoli, Gus'kov, Rupasov, Andreoli, Cristofari and Di Giorgio2015; Cipriani et al., Reference Cipriani, Gus’kov, Consoli, De Angelis, Rupasov, Andreoli, Cristofari and Di Giorgio2018).
Heat conduction without hydrodynamics
The curves of Figure 1 are taken at different times in the simulation. The dynamics of the heat conduction wave is different before and after the time instant t h = 1.62 ns, which corresponds to the homogenization of the region heated by the laser radiation. At the beginning of the laser irradiation, the foam absorbs the laser energy on a depth equal to the opacity length, while the homogeneous medium absorbs it at the front of the target. The time required for the foam plasma to become homogeneous delays the formation of the heat wave in panel (a) compared with panel (b). Ahead of the temperature front, the laser-produced foam plasma has formed but it is not homogeneous and the heat conduction is limited proportionally to the degree of homogenization; behind it the homogenization process has been completed and the heat conduction is fully operational. After the homogenization time t h, the heat wave speed in the homogeneous medium is larger than in the foam: the speed of the thermal wave is 3.3 × 107 cm/s in the homogeneous medium, while it is 2.2 × 107 cm/s in the foam, with a ratio of 1.5. Thus, the limit on the electron conductivity has a very important effect on the speed of the ionization wave.
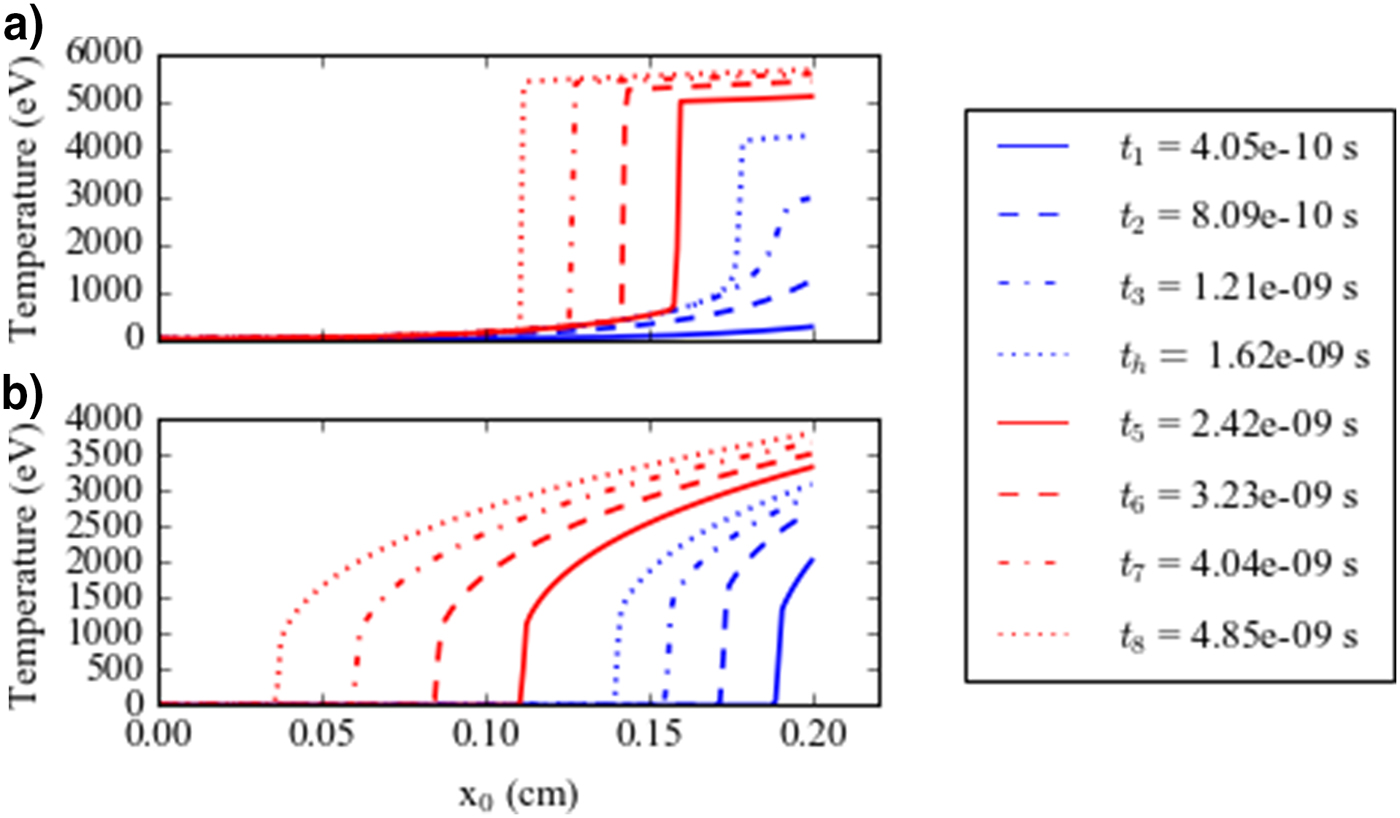
Fig. 1. The temperature profiles in the simulation of a large-pore overcritical foam with the parameters described in the text. The hydrodynamics is suppressed. Panel (a) represents the temperature for a foam target; panel (b) represents the temperature for a homogeneous target with the same density as the foam one. The curves are taken at the different times of the simulation reported in the legend. The laser is coming from the right. In all panels, the horizontal axis corresponds to the position of the numerical cells at the initial time t 0.
Hydrodynamics without heat conduction
Comparing panels (a1) and (a2) of Figure 2, we can see that the delay in the laser absorption due to homogenization is found also in the formation of hydrodynamic wave in the foam. In panel (a2), the shockwave appears already at the initial time, while in the foam, it is visible only at homogenization time t h = 1.52 ns. The compression wave appears later in the foam than in the ordinary homogeneous material. The wave is slightly slower in the foam than in the homogeneous medium. The position of the front of the compression wave is almost coincident in the two cases from the homogenization time on. This shows that the modification of Eq. (8) leads to physically correct results, which result in no delay of the compression wave propagation in the porous target, as well as lower peak of the density and larger peak of the pressure at the wave front in comparison with homogeneous medium.
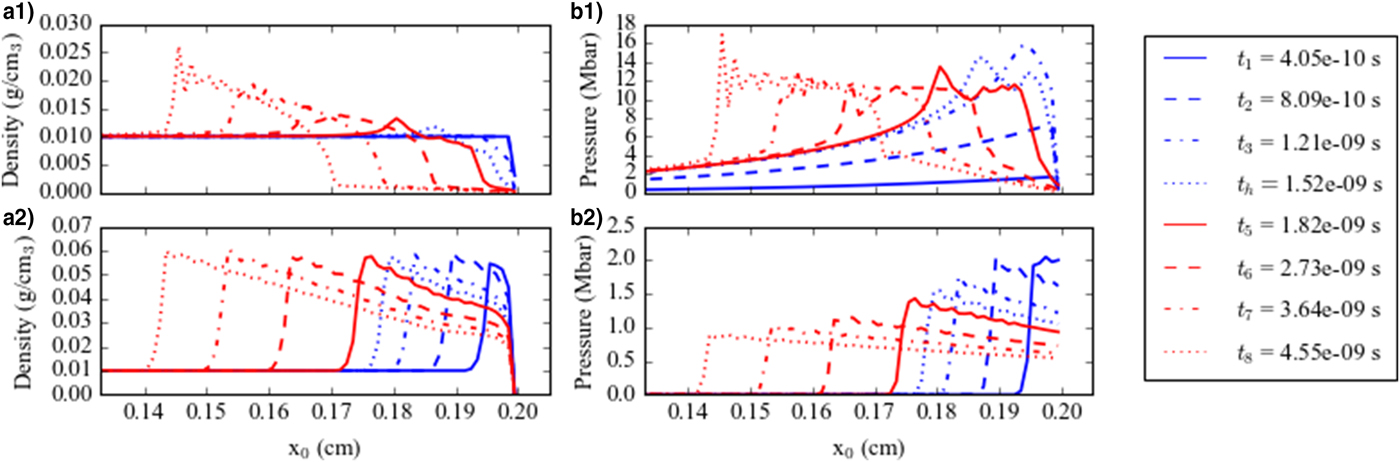
Fig. 2. The density profiles in the simulation of a large-pore overcritical foam with the parameters described in the text. The heat conduction is suppressed. Panels (a1) and (b1) represent the density and the pressure for a foam target; panels (a2) and (b2) represent the density and the pressure for a homogeneous target with the same density as the foam one. The curves are taken at the different times of the simulation reported in the legend. The laser is coming from the right. In all panels, the horizontal axis corresponds to the position of the numerical cells at the initial time t 0.
Complete simulation
Figure 3 reports the simulation results with all the physical processes active. The features found in the previous subsections are all apparent. The density profile in (a1) shows that the hydrothermal wave in the foam develops later than in the homogeneous medium, in panel (a2). Panel (b1) also shows the effect of electron conductivity suppression, giving a sharp front of the heat wave and a slow-down of its propagation speed, compared with the homogeneous medium in (b2). The peak value of the pressure in (c1) can be estimated to be around 30 Mbar, and it is higher than the value of 12 Mbar in (c2). This fact can be explained by considering that the absorption wave and the hydrothermal wave propagate more slowly in the foam compared with the homogeneous medium and, therefore, in the former the absorbed and transferred energy is contained in a smaller volume compared with the latter. For times later than the homogenization time t h = 1.72 ns, we can see from panels (a1) and (a2) that the hydrothermal wave moves into the target with a very different speed, as does the heat wave. The speed of the hydrothermal wave in the foam is 1.3·107 cm/s, which is less by factor 2.6 than the shock wave speed in the homogeneous medium (3.4·107 cm/s). This shows that the low conductivity of the non-homogeneous foam plasma deeply affects the propagation speeds of these two waves.

Fig. 3. The profiles of the different physical quantities in the simulation of a large-pore overcritical foam with the parameters described in the text. Panels (a1), (b1), and (c1) represent density, temperature, and pressure respectively for a foam target; panels (a2), (b2), and (c2) represent density, temperature, and pressure, respectively, for a homogeneous target with the same density as the foam one. The curves are taken at the different times of the simulation reported in the legend. The laser is coming from the right. In all panels, the horizontal axis corresponds to the position of the numerical cells at the initial time t 0.
Small-pore foams of subcritical density
In these simulations, the pore size is taken δ0 = 1 μm, corresponding to a solid part thickness b 0 = 0.025 µm [see, (1)]. The initial geometric transparency length results to be L 0 = 12.3 µm [see, (3)]. The conditions of simulations correspond to the experiments recently performed at PALS, GEKKO, and OMEGA nanosecond laser facilities.
The results of the simulations with a subcritical foam target are reported in Figure 4. The speed of the hydrothermal wave in small-pore foam of subcritical density is about 2.9·107 cm/s that is 1.5 times lower than the speed of the ionization wave in the homogeneous medium of the same density (4.5·107 cm/s, the same as shock wave speed in the Small-pore foams of subcritical density section), as can be seen from the temperature and density profiles in panels (a1) and (a2), and (b1) and (b2), respectively. Due to the small optical depth of the considered small-pore foam, the temporal dynamics of hydrothermal wave is closer to the case of homogeneous substance in comparison with large-pore case. In fact, in large-pore foams, the homogenization process requires a longer time to be completed, and this results in an effective slow-down of the hydrothermal wave. Heat conductivity and response to pressure gradients are limited during the homogenization stage, and thus the propagation speed of the heat and compression waves is reduced. In small-pore foams, the homogenization time is very small and the limiting on the heat conduction and pressure is confined to a thin layer. Therefore, the hydrothermal wave speed in this last case is also reduced, but the slow-down is less effective than in large-pore foams.

Fig. 4. The profiles of the different physical quantities in the simulation of a small-pore subcritical foam with the parameters described in the text. Panels (a1), (b1), and (c1) represent density, temperature, and pressure, respectively, for a foam target; panels (a2), (b2), and (c2) represent density, temperature, and pressure, respectively, for a homogeneous target with the same density as the foam one. The curves are taken at the different times of the simulation reported in the legend. The laser is coming from the right. In all panels, the horizontal axis corresponds to the position of the numerical cells at the initial time t 0.
Additional results
Table 1 presents a summary of the results of simulations performed to investigate the dependence of the hydrothermal wave properties on the intensity of laser radiation and foam density for both subcritical and overcritical media.
Table 1. Hydrothermal wave speed and homogenization time for various simulation parameters, in comparison with an equivalent homogeneous medium

Along with the simulations of a supercritical foam with a density of 10 g/cm3 and intensity 1014 W/cm2, two sets of additional simulations were done. The first one regards the laser intensity I = 1013 W/cm2, one order of magnitude lower than in previous simulations (the first line of the results of Table 1). In the second set of simulations, the foam density was reduced to ρp = 5 g/cm3.
Decreasing the laser intensity, as well as increasing the foam density, reflect in a slow-down of both the homogenization process and the propagation of the hydrothermal wave for all types of foams (large-pore, small-pore, overcritical, and subcritical). The general reason is the decrease of the temperature in the heated region. Decreasing the laser intensity of one order of magnitude at the same density leads to 4–5 times increase of homogenization time for large-pore foam and 2–3 times increase for small-pore foam. Hydrothermal wave speed decreases, approximately, by a factor 5 in large-pore foam and by a factor 3–3.5 in small-pore foam. An increase of the foam density at the same intensity leads to an increase of the homogenization time of 1.5–2 times for both large-pore and small-pore foams. The hydrothermal wave speed decreases by, approximately, the same factors. In the large-pore foam case, the factor of decrease of the hydrothermal wave speed due to the decreasing of laser intensity is 1.5–2 times larger than for homogeneous media of the same density and this factor is, approximately, the same for small-pore foam and homogeneous media (about 2.5–3). The factor of hydrothermal wave speed decreasing due to the increase of the density is, approximately, the same (1.2–1.5).
As noted at the end of subsection “Complete simulation”, the pressure realized in overcritical foams is larger than the one obtainable in a homogeneous medium of the same density. From Figure 5, it can be seen that, starting from 5 mg/cm3 for large-pore foams and from 10 mg/cm3 for small-pore foams, the pressure is larger than in the homogeneous medium, even more than two times and becomes more important at larger densities. This supports the idea of using porous media as absorbers to increase compression in the substrate in a layered target configuration.
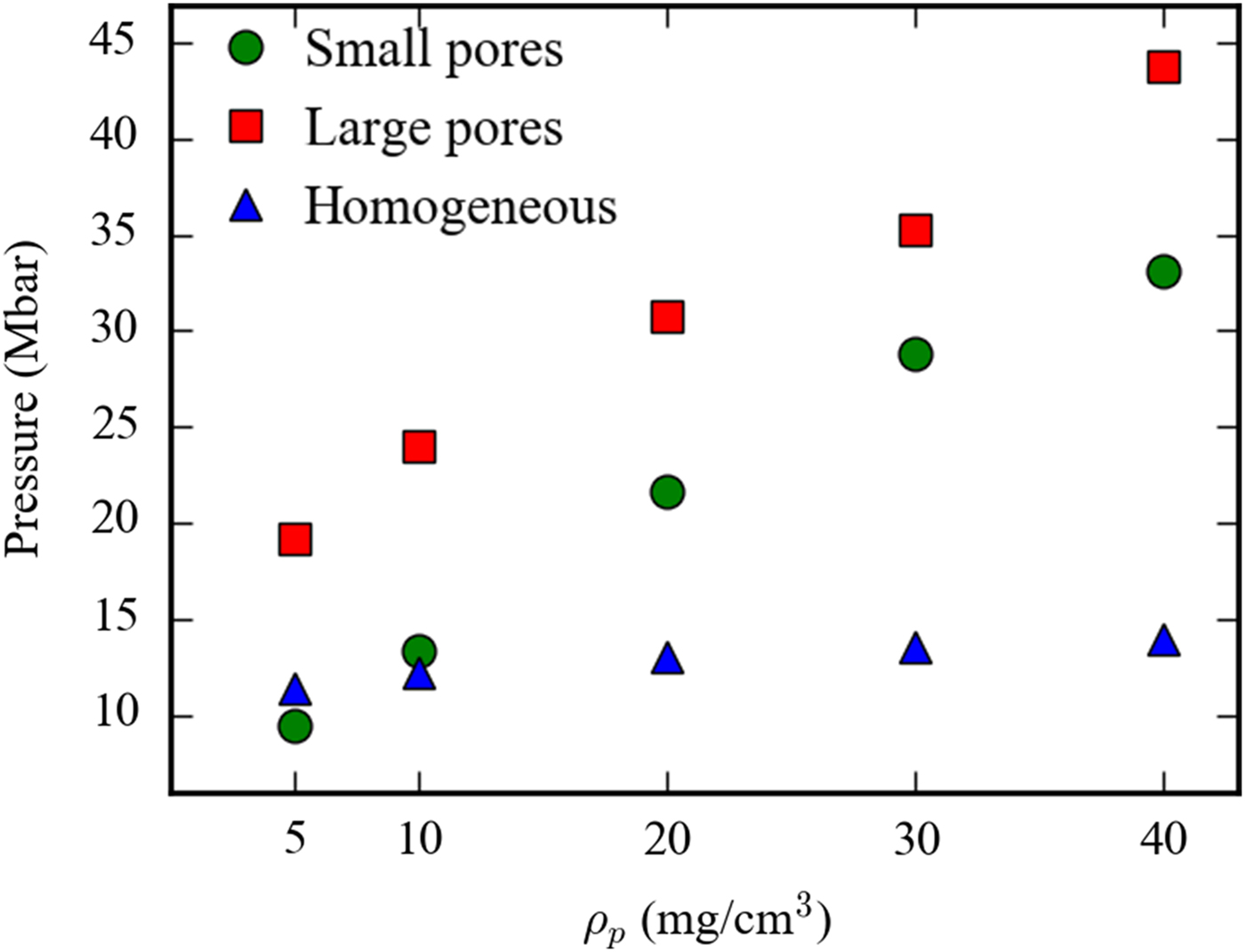
Fig. 5. The maximum value of the pressure for different initial average densities for large-pore (40 µm) and small-pore (1 µm) foams and equivalent homogeneous media. The target in all the simulations is thick enough to ensure that all the laser energy is absorbed during the simulation time.
Comparison with experiments
Simulations were carried out in the conditions of recent experiments on the terawatt laser beam interaction with flat porous targets, performed at Gekko-XII (Nicolai et al., Reference Nicolai, Olazabal-Loumé, Fujioka, Sunahara, Borisenko, Gus'kov, Orekov, Grech, Riazuelo, Labaune, Velechowski and Tikhonchuk2012) and PALS (Borisenko et al., Reference Borisenko, Akimova, Gromov, Khalenkov, Merkuliev, Kondrashov, Limpouch, Kuba, Krousky, Masek, Nazarov and Pimenov2006; Khalenkov et al., Reference Khalenkov, Borisenko, Kondrashov, Merkuliev, Limpouch and Pimenov2006) installations with foams of subcritical density, and at the ABC installation with foam of overcritical density. All the foams used in the Gekko-XII and PALS experiments have practically the same chemical composition, corresponding to an average atomic weight of about 7.2 and an average charge of fully ionized plasma 3.8, and also have practically the same density of solid elements about 1 g·cm−3. In these experiments, the main measurable result is the velocity of the energy transfer wave, which was determined from the temporal evolution of the image of the heated plasma with the help of X-ray streak camera, and also by recording the emission from the rear side of a foam layer of a given thickness. The experiments performed at the Gekko-XII laser facility were done with a small-pore subcritical foam with average density of 10 mg cm−3 and average pore size of 1 µm. The Gekko-XII laser beam had a total energy of 300 J of 350 nm wavelength radiation (third harmonic of Nd-laser radiation) and with a 100 µm focal spot radius. The pulse down time was 3 ns. The intensity calculated from these parameters is of about 3·1014 W/cm2. The ionization wave velocity measured in these experiments is 2.9·107 cm/s. The speed of the hydrothermal wave calculated by the MULTI-FM code is 4.9·107 cm/s. The fractal parameter is taken equal to 0.8. In these conditions, in an equivalent homogeneous substance, the ionization wave velocity would be 6.6·107 cm/s. The simulations with the PALE code gives a velocity of 3.6·107 cm/s. In the PALE code, the characteristic temperature on the front was about 1.5 keV, in the MULTI-FM code is of 1.9 keV.
Similar experiments have been carried out at PALS laser facility. The laser pulse had a wavelength of 438 nm (third harmonic of iodine-laser radiation), a FWHM duration of 320 ps, with a 400 µm focal spot radius and a total energy about of 170 J. These parameters provide the intensity of about 7·1014 W/cm2. The experiments were carried out with small-pore subcritical foams of density of 9 and 4.9 mg cm−3, and a pore size of about 1 µm, as well as in the experiments at the Gekko-XII installation. The measured velocities of the ionization wave were 3.3·107 cm/s for the 9 mg cm−3 foam and 1.8·108 cm/s for the 4.9 mg cm−3 foam. In the calculations using the PALE code, the speeds were 5·107 and 2·108 cm/s, respectively. In the simulations with the MULTI-FM code, the speeds are 7.4·107 cm/s for a foam with a density of 9 mg cm−3 and 1.9·108 cm/s for a foam with a density of 4.9 mg cm−3. In an equivalent homogeneous media, the velocities of the ionization wave would be 9.9·107 and 2.5·108 cm/s. The difference in the results from the two codes is mainly due to the fact that MULTI-FM is a one-dimensional code, while PALE is a two-dimensional code. A two-dimensional calculation is able to reproduce also the lateral energy spread in the target, which contribute to slowing down the hydrothermal wave; this effect cannot be taken into account in a one-dimensional code. Nonetheless, in MULTI-FM simulations, the hydrothermal wave speed is significantly lower in the foam than in the homogeneous medium and it is mostly quite close to the experimental number, demonstrating that the main effects of plasma homogenization are properly taken into account.
In the experiments carried out at the ABC facility at the ENEA Research Center in Frascati (Cipriani et al., Reference Cipriani, Gus’kov, Consoli, De Angelis, Rupasov, Andreoli, Cristofari and Di Giorgio2018), a foam target of 10 mg/cm3 has been irradiated with the beam of Nd-laser radiation, with a 100 µm focal spot radius, total energy of 40 J, and pulse duration of 3 ns. These parameters provide the intensity of about 4·1013 W/cm2. The diameter of the pores of the foam target was around 40 μm and solid element radius of about 1 μm. In this case, the investigated foam was a large-pore overcritical one. The measured energy transfer wave velocity was 1.5·107 cm/s. The hydrothermal wave velocity calculated by the MULTI-FM code is 1.7·107 cm/s, while in the equivalent homogeneous target, the velocity of the shock wave results to be 2.7·107 cm/s.
Conclusions
The action of terawatt laser pulse of nanosecond duration on a low-density porous substance of light chemical elements has been studied by using the newly developed one-dimensional hydrodynamic MULTI-FM code, with target densities from values less than the critical plasma density for the given laser radiation wavelength, to values exceeding the critical density. The properties of the plasma produced in these conditions have been investigated in the various regimes of pore sizes and densities. The results of MULTI-FM code simulations are in a good agreement with experimental data and the discrepancy found in the comparison is mainly due to the fact the MULTI-FM is a one-dimensional code. This limits the capability of reproducing the lateral spread of the energy inside the target and also to model the deflections of the laser rays passing through the foam material, leading to an overestimation of the velocity of the hydrothermal wave. Nonetheless, as seen above in the comparison with experiments, MULTI-FM is able to catch the main characteristics of the physical picture. The experimental results together with the results of MULTI-FM code simulations confirm that the energy transfer in these materials is realized by the propagation of the hydrothermal wave, whose velocity is close to the sound velocity in the heated region of the substance. This velocity is significantly lower than the velocity of the laser-supported ionization wave or the electron thermal conductivity wave, respectively, in a homogeneous substance of equivalent subcritical or overcritical density. Moreover, the speed of hydrothermal wave increases with the growth of laser intensity and with the decrease of the initial average density. Finally, the pressure behind the front of the hydrothermal wave in the porous substance is larger, and the density, on the contrary, is less in comparison with the shock wave in a homogeneous substance of equivalent overcritical density. These results are of key importance for the application of low-density foams as absorbers of laser radiation, for effectively smoothing the heterogeneities of laser energy deposition in the LTF targets, and as effective ablators, to enhance the compression.
The code can be further improved in the future. The approximations made to model the electron conductivity and the pressure response limitations can be refined, as well as the assumptions on the transition in the absorption coefficient between foam-like and inverse bremsstrahlung absorption. Finally, the model can be implemented in two-dimensions to better model the laser propagation inside the target and the lateral energy spread.
Acknowledgment
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training program 2014–2018 under grant agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. This work was supported by the Program of Increase in the Competitiveness of the National Research Nuclear University MEPhI. The work of S. Gus'kov and A. Rupasov was also supported by Russian Foundation for Basic Research project No. 17-02-00059-а.








