Proposed laser fusion power plant concepts suffer from the huge size and expense of the lasers needed for compression and ignition. In a 1969 study (classified in 1970 and declassified in 2007), the idea to use chemical high explosives for the pumping of megajoule lasers was explored. Apart from being less expensive by orders of magnitude, such lasers are expected to be much more compact, and with their large energy, output could simultaneously drive several thermonuclear micro-explosion chambers. Because of its topical importance, I accepted the journal's invitation to publish a previously classified work, but with new unpublished ideas, with the previously classified paper put into the appendix.
The advantage of lasers (Nuckolls et al., Reference Nuckolls, Wood, Thiessen and Zimmermann1972; Brueckner Jorna, Reference Brueckner and Jorna1974) for inertial confinement fusion (ICF) power plants is their good standoff property from the thermonuclear micro-explosion. A disadvantage is the enormous size and high cost, primarily because of the laser's inefficiency. Electric pulse power ICF drivers (Winterberg, Reference Winterberg1968; Yonas, Reference Winterberg1978) depend on transmission lines connecting the pulse power source with the thermonuclear target. Following each micro-explosion, the transmission lines have to be replaced. This leads to the build-up of large, low intensity, radioactive waste. In addition, the neutron slowing down and absorption in the transmission lines leads to blast waves inside the micro-explosion chamber. The only other ICF driver, which, about a good standoff property, can compete with a laser, is impact fusion (Winterberg, Reference Winterberg1966; Maissonier, Reference Maissonier1966). Unlike lasers, impact fusion drivers have a high efficiency, but they need a several tens of km long magnetic traveling wave macro-particle accelerator.
The energy needed to ignite a thermonuclear reaction in liquid (or solid) deuterium-tritium (DT) is not that large. Estimates made on the safe side suggest an energy of not more than 10 MJ = 1014 erg, about the same amount of chemical energy stored in a few liters of a combustible liquid. The problem, of course, is that this energy must be compressed in space (down to an area less than a cm2), and in time (to a time less than 10−8 s).
The large density of chemically stored energy (on the order~1011 erg/cm3) and the speed it can be released in the detonation of a high explosive raises the question, could this energy be used to pump a laser. It would be ideal to have a high explosive where all the chemical energy is transformed into a flash of coherent light, instead into kinetic energy and heat of a fast moving detonation wave. In the real world, such an explosive does not exist, or if it exists (perhaps in the triplet state of helium), it is expected to be highly unstable. This does not mean that there are no high explosives where at least part of the energy can be directly converted into a laser pulse, but this is not the only possibility to pump a laser with a high explosive. Instead of using the explosively released energy directly, one may use it to pump some lasing material spatially separated from the high explosive.
For the direct conversion of the chemical energy into a laser pulse, the high explosive must be simultaneously ignited throughout the entire volume it occupies. Otherwise detonation waves will develop, leaving behind a medium in thermodynamic equilibrium without a population inversion. This problem may be overcome by giving the high explosive a layered structure, with the thickness of the layers larger than the optical path length at low laser radiation intensities, but transparent at high laser radiation intensities (condition for self-induced transparency). The volume ignition of high explosive could be done by an intense flash of light passing through the gaps separating the layers from each other. Azides of dioxitanes are high explosives, which might be suitable for this purpose. Both are the source of intense luminescent radiation. Other interesting candidates are noble gas compounds. As explosives, they too have higher energy densities compared with conventional explosives.
Figure 1 shows how the direct conversion of chemical energy into laser energy can be implemented. The high explosive is arranged in a layered zigzag pattern, ignited from both sides with triggered flash lamps. The expansion of the high explosive helps to sustain a high population inversion until the last moment where an auxiliary short pulse laser triggers a photon avalanche in the population-inverted medium made up from the burnt explosive.

Fig. 1. (a, b) Argon bomb pumped dye laser: L laser rod, A solid argon, HE high explosive, L focusing lens, T thermonuclear target.
Glass lasers can be efficiently pumped with argon flash lamps, because at a temperature of a few eV, argon is a brilliant light source. In the argon flash lamp, argon has a low density. A much more powerful light source is an argon bomb, where a detonation wave from a high explosive goes into solid argon. Such an argon bomb can pump a laser, which is powerful enough to ignite a thermonuclear micro-explosion. Because hot argon emits light in a broad spectrum, one may choose a dye laser with a large number of upper laser level states.
One possible configuration for an argon bomb dye-laser is shown in Figure 2a. There the laser rod is in the center of a cylindrical configuration surrounded by solid argon and high explosive. A problem with this configuration is that the thickness of the solid argon must be less than the optical path length in it at the temperature of a few eV, where the light emission is strongest. This requires a rather thin layer of solid argon, which is not thick enough to release the many photons required to pump the laser rod to an energy of ~107 J. One can overcome this problem by a layered structure shown in Figure 2b, where each argon layer is sufficiently thin to make it transparent. There are then many laser beamlets emitted from each layer, which have to be focused by a Fresnel lens onto the thermonuclear target.

Fig. 2. (a, b) Argon bomb pumped dye laser: L laser rod, A solid argon, HE high explosive, L focusing lens, T thermonuclear target.
With a population inversion in a dye-laser on the order 10−2, an atomic number density on the order n ~ 1022 cm−3, an upper laser level energy of ~0.1 eV–10−13 erg, the energy density of the pumped laser rod would be ~107 erg/cm3, requiring a volume of 10 cubic meters to store ~1014 erg = 107 J. If the fraction f of the explosively released energy is converted into photons emitted by hot argon, the volume of the high explosive with an energy density of ~1011 erg/cm3 needed to pump the laser to ~1014 erg, would be V ~ (1014/1011)/f cm3; assuming that f ~ 10−1, one has V ≈ 104 cm3 with an energy of V × 1011 erg/cm3 = 1015 erg. This is equivalent to 100 kg of TNT.
A very different way a laser can be pumped by a high explosive is with a magneto-hydrodynamic dynamo generating multi-megampere currents, which have to pass through a lasing material. This concept is related to explosively driven magnetized target fusion, discussed by Jones and von Hippel (Reference Jones and von Hippel1998) as a means to ignite a large thermonuclear explosive device without using a fission trigger.
Because of the high energy density of chemical explosives, lasers driven by them would be much more compact than conventional lasers, like those that are driven by flash lamps, for example. The price paid for this advantage is that the laser must be replaced following each thermonuclear micro-explosion, but unlike the replacement of the debris from a disposable transmission line in electric pulse power driven thermonuclear micro-explosions this debris is not radioactive.
To compensate for the cost of the explosively driven disposable lasers, the laser not only should be very robust, but also should release much more energy than conventional lasers with which it has to compete. In a laser driven with high explosives, the laser beam can then be split into several beams, with each beam igniting a thermonuclear micro-explosion in one of several micro-explosion combustion chambers.
In the appendix, the recently declassified work is reproduced in its entirety. In this study (now 38 years old), it was already proposed to employ mega gauss magnetic fields to facilitate the formation of a hot spot for the fast ignition of the thermonuclear explosive. This same idea was also used in a proposed hot spot ignition of a dense z-pinch, in a paper by Winterberg (Reference Winterberg1981), and in later studies of a shear flow stabilized z-pinch (Winterberg, Reference Winterberg1999).
The paper already showed that one needs a petawatt laser for thermonuclear ignition. While this is difficult to achieve with conventional lasers, this may be much easier for lasers driven by high explosives. There the laser beam energy can be larger by orders of magnitude. Even though the paper mentions the significance of a strong magnetic field to reduce the energy needed for ignition, it does not mention the idea to ignite a thermonuclear detonation wave along a high current z-pinch. This idea was published at the same time somewhere else (Winterberg, Reference Winterberg1969).
APPENDIX
Can a laser beam ignite a hydrogen bomb?
It is shown that, although it still seems to be confronted with considerable technological difficulties, the possibility of igniting a thermonuclear explosion by means of an intense laser beam must be considered seriously. Because of the minimum energy in excess of 1014 ergs required to trigger a thermonuclear explosion, ordinary lasers are unsuitable for this purpose. The enormous energy requirement suggests the development of rare gas ion lasers, in which the optical excitation is performed in the liquid state by powerful shockwaves generated by chemically driven implosions. An alternative for the explosive excitation is an electric discharge by an explosively driven high current generator. Finally, chemical lasers operating at high densities may approach the required conditions. If such a system should turn out to be feasible, it would probably not qualify for military applications because of its large trigger mechanism involving probably tons of high explosives; its significance will rather be for Plowshare applications and perhaps “clean” nuclear bomb rocket propulsion.
1. INTRODUCTION
It is generally known that the mechanism by which a hydrogen bomb operates is based on a fission trigger, which in essence is an “ordinary” atomic bomb using Uranium 235 or Plutonium. The explosion of the atomic bomb produces (1) the required ignition temperature for the thermonuclear reaction process and (2) an energy in excess of the required energy to ignite a sufficiently large quantity of the thermonuclear material. Both requirements are necessary in order to set off a thermonuclear detonation.
Since giant pulsed lasers can fulfill the first condition, the question is frequently raised whether lasers at some future time would become big enough to satisfy also condition 2 leading to the prospect of a “laser bomb.” We will show below that for this second condition to be satisfied, energies of at least 1014 ergs = 107 J haves to be delivered in less than 30 ns to a fraction of a cm3 of the thermonuclear material. Although the required time scale is well within the art of laser technology, the biggest lasers are still orders of magnitude away from the minimum required energy of 10 MJ. For example, with Neodynium doped glass lasers energy outputs of 103 J have been achieved, which are still at least four orders of magnitude away from the required goal. To increase these lasers simply by a factor of 104 in size would make them unappealingly large and, therefore, unfeasible for reasons of technical limitations.
In spite of this pessimistic assessment, there seems to be a theoretical possibility by which the output of a laser can be increased substantially. This can be accomplished by strong chemical explosions energizing the laser material. In this case, however, the laser would be destroyed by the force of the explosion. A scheme of this sort will therefore, resemble a thermonuclear bomb with a fissionless trigger.
2. THE TRIGGER CONDITION
It was pointed out in the introduction that there are two basic conditions for the ignition of a thermonuclear explosive. In more precise terms, these conditions can be formulated as follows: (1) the energy required for ignition must be supplied to the thermonuclear material in a time which is short compared to the time in which the material can lose its energy by radiation, and (b) after the material is heated up to thermonuclear temperatures, the detonation condition must be satisfied, which requires that the fusion products are stopped within the heated region of the thermonuclear material. Because the ignition temperature itself depends upon the efficiency by which the energy of the fusion products can be fed back into the heated plasma, condition a and condition b are interdependent.
For the following, we shall assume that the thermonuclear material is a liquid respectively, solid deuterium-tritium (T-D) mixture with an atomic number density of N = 5 × 1022 cm−3. We will furthermore express temperatures in units of keV. If the region to be heated up is sufficiently large, losses by expansion or electronic heat condition are small and are then predominantly determined by Bremsstrahlung. The characteristic loss time for Bremsstrahlung which is given by
determines the time scale in which the target is to be heated up to thermonuclear temperatures. For T = 10 keV one obtains τR = 57 ns. According to the first condition, the trigger energy has thus to be supplied in a time which is shorter than this time, for example, in the time τ= 10 ns. For the second condition to be satisfied, we observe that if the range of the fusion products is λ, the probability P for the fusion products to be stopped inside a spherical volume of radius r0 is given by
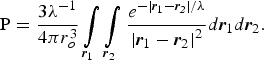
This double integral has to be taken over the entire sphere. With x = rO/λ, this integration yields
The condition for detonation must be combined with the energy losses to obtain the minimum energy which is required for the ignition of a thermonuclear explosion. It should be emphasized that the minimum energy is not attained at the smallest possible ignition radius, since the smallest possible radius may be connected with a higher ignition temperature that takes into account the higher losses of charged fusion products from the reaction region. The energy production of the T-D reaction can be expressed in the form
In order to determine the fusion energy output reabsorbed by the target, one must multiply the right-hand side of Eq. (4) by the probability P(x) that the fusion reaction products will remain within the target. The energy input from the fusion products has then to be balanced by the Bremsstrahlung losses, which is the condition for ignition.
For fully ionized hydrogen plasma, the Bremsstrahlung losses are given by
We thus obtain as the condition for the ignition and detonation of a T-D thermonuclear reaction the equation
where, as before, x = rO/λ. The range λ of the He4 fusion product from the T-D reaction is given by
In a situation where detonation can occur, Eq. (6) has two roots. The smaller root, which gives the ignition temperature, approaches T = 4.3 keV for r0 = ∞ and P(x) = 1. The solution of Eq. (6) gives the function T(r0) connecting the temperature and radius at which detonation occurs.
The energy input which must be supplied from outside to reach the ignition temperature is given by
The functions T(r0) and E(r0) are shown in Figure 1. The input energy for the T-D reaction (Fig. 1b) has a sharp minimum at r0 = 2.1 mm with an energy of 1.12 × 1014 erg. The ignition temperature at this point is 12.1 keV and P(x) = 0.108. About 90% of the fusion product energy is dissipated into the volume surrounding the reacting region.

Fig. 1. Ignition temperature and input energy for small DT fusion explosions.
The smallness of the minimum radius of r = 2.1 mm makes it necessary to consider losses by electronic heat conduction unless an energy is supplied to the thermonuclear material not far in excess of the required minimum 1014 ergs dissipated into a correspondingly larger volume. The characteristic loss time for electronic heat conduction is given by
For r0 = 0.21 cm and T = 10 keV one has τC = 0.7 × 10−8 s, which is about the same order of magnitude as the radiation loss time Eq. (1). However, in contrast to the radiation loss time, the electronic heat conduction loss time can be substantially reduced by applying a strong magnetic field to the volume to be heated up to thermonuclear temperatures. In the presence of a strong magnetic field, the heat conduction is reduced by the factor
If, for example, H = 106 gauss and T = 10 keV, one would obtain χ⊥/χ = 1.7 × 10−1 and the electronic loss time would be increased to τC ⊥ = 4 × 10−8 s, which is an order above the radiation loss time. For a field of 3 × 106 gauss, which is well attainable with explosively driven high current generators (Knoepfel et al., Reference Knoepfel, Kroegler, Luppi and van Montfoort1969), the reduction would be χ⊥/χ = 1.9 × 10−2 and τC ⊥ = 3.6 × 10−7 s. It is therefore obvious that for ignition energies not greatly in excess of 1014 ergs, which would imply a large r0 and, according to Eq. (9) correspondingly large τC, the application of a strong magnetic field will be desirable.
3. THE PHYSICAL REQUIREMENT AND POSSIBILITIES ON THE LASER SIDE
Besides the requirement of a total energy output in excess of 10 MJ to be delivered in about 10 ns, the photon beam must have a proper frequency to ensure efficient energy absorption in the thermonuclear material. Since the minimum energy input corresponds to a spherical volume about 1/2 cm in diameter, the absorption length of the photon beam must be of the same order. The absorption length has been derived for a fully ionized plasma by Dawson and Oberman (Reference Dawson and Oberman1962) and is given by (λ wave length of the laser light)
For a hydrogen plasma with Z = 1 and N × 5 × 1022 we have
Since the minimum radius of the thermonuclear material to be heated was about r0 = 0.2 cm, we request for a perfect energy absorption l = 0.2 cm. For T = 10 keV, because of Eq. (12) this then results in λ = 2.15 × 10−5 cm = 2150Å, which is located in the ultraviolet. For longer wavelengths, the absorption of the laser energy will be less efficient since it is concentrated more in a surface layer, but it is conceivable that even then, a large energy deposition is possible by means of a shock wave propagating from the surface into the thermonuclear material. The general rule, however, is to look for lasers operating at a short wave length.
The maximum energy output of a laser is reached if a complete population inversion is achieved. In order to get a large population of upper laser levels per unit volume, the laser material has to be preferably in the liquid or solid state. To estimate the maximum energy, which can be pumped into the liquid or solid state, we assume a complete population inversion of all states. Since a liquid or solid has an atomic number density on the order N ≈ 1022 cm−3 and since the laser transition will set free an energy on the order 1 eV ≈10−12 erg, this implies an energy storage capacity of 1022 × 10−12 = 1010 ergs/cm3. This then means that in 10 liters of laser material, an energy of 1014 erg = 10 MJ can be stored. Because a complete population inversion cannot be expected for reasons of incomplete efficiency, a volume 10 times larger is a more realistic estimate. Hence, about 100 liter of activated laser material will approach the critical energy dimensions needed to ignite a thermo-nuclear detonation.
4. THE DIFFERENT METHODS BY WHICH A LARGE POPULATION INVERSION CAN BE ACHIEVED IN DENSE MATTER
There seem to be three different methods by which a large population inversion can be achieved. In the first method, the laser material is activated by strong shock waves from chemical high explosives. In the second method, the laser material is activated by a powerful electrical discharge by means of an explosively driven high current generator. In the third method, the population inversion is accomplished as the result of a chemical explosion in the laser material itself. In this case, the reaction products are created in an excited state, which is an upper maser level. This scheme is known as a chemical laser.
Since the most powerful steady state laser known to date is the CO2 gas laser, one might expect that the activation of liquid CO2 may lead to a large population inversion. It is, however, doubtful that this can be accomplished since an elevated temperature in CO2 will populate the lower maser levels blocking the laser transition from the upper level. Moreover, the CO2 laser line is located in the infrared, which is a disadvantage for an efficient energy deposition. The same problem most likely will exist for most chemical laser, which work in the infrared by molecular transitions.
For these reasons, it seems that the most promising candidates are the noble gas ion lasers. The shortest reported laser wavelength has been for NeIV with λ = 2358Å which is located in the ultraviolet and, by coincidence, satisfies our requirement for most efficient energy deposition. Since it will probably be difficult to produce four times ionized Neon by the methods under consideration, a better candidate is likely to be the Argon ion laser of singly ionized Argon. The shortest reported laser line for the Ar+ ion laser is in the visible blue at λ = 4879Å.
Because the Ar+ ion has fewer low-lying energy levels than would normally exist in molecules, the blocking of the laser transition by population of the lower levels is less likely to occur. We will assume that liquid Argon is heated up to a temperature of T = 90000°K. Liquid Argon has a density of ρ = 1.404 g/cm3. For T =9 × 104 °K, the pressure is P = 2.55 × 1011 dyn/cm2 = 2.9 × 105 atm. The ionization potential of Argon is Vi = 15.7 eV. With the Saha equation on then computes an ionization degree of x ≈ 50%. From this value it does not seem impossible to expect a population inversion of 10% for the upper laser level.
The population of the upper laser level can be enhanced by the so called entrapment of radiation which will occur at even lower densities than under consideration. The entrapment of radiation will make a photon be emitted and resonance-reabsorbed many times inside the laser material. This entrapment of radiation will result in an increased effective life time for the upper laser level which is of importance for a large population inversion.
There is, however, another serious problem in conjunction with the operation of high densities and that is the possibility of approaching black body conditions. In this case, no laser action is possible. Black body conditions are more likely to occur in systems with a high density of energy level such as molecules. It is not known if Ar+ at liquid densities and temperatures of l05 °K is in such a state.
4.1. The first method
In the first method, it is intended to heat the laser material by means of a strong shockwave of chemical explosive.
The temperature behind a strong shock wave in singly ionized plasma is given by
where A is the atomic weight, R is the universal gas constant, and γ is the specific heat ratio. v is the shock velocity. For an Argon plasma, A = 40. We furthermore put v = 8 × 105 cm/s, which is the detonation velocity of hexogen. We thus have from Eq. (13) T ≈ 3 × 104 °K. This is lower by a factor of three than the temperature of 9 × 104 °K, which is required to obtain 50% ionization in Argon. Since at a temperature of 3 × 104 °K, the degree of ionization would be only 2.5%, it is obvious that a higher temperature is required.
It is well known that the temperature behind a strong shock wave will rise as r−0.4 for a cylindrical, and as r−0.8 for a spherical convergent shock, where r is the radial distance of the shock wave from the center of convergence (Guderley, Reference Guderley1942). Since the laser rod shall have cylindrical symmetry, a cylindrical convergent shock wave seems to be most suitable for our purpose. If the laser rod has a radius of r0= 10 cm, the high explosive has to be arranged in a cylindrical shell separated from the center of convergence by a radius r1 = 100 cm in order to get a rise in temperature by about a factor of three. The situation is drawn schematically in Figure 2.

Fig. 2. Cylindrical arrangement of high explosive and Cylindrical laser rod for convergent shock wave heating.
The question of population inversion behind a strong shock wave requires some remark. It is clear that in complete thermodynamic equilibrium, there is no population inversion. However, the situation is quite different in the material just behind a strong shock wave. Immediately behind the shock wave, one has a uniform isotropic velocity distribution rather than a Maxwellian. If the population inversion is achieved by a resonant cross section of atomic particle collisions at a certain energy, and if the particles behind the shock front posses just this energy, by making a proper choice of r0 and r1, then a large population inversion is quite well conceivable.
4.2. The second method
In the second method, the laser material is energized by a powerful gas discharge by an explosively driven high current generator. Such generators have been reported in the scientific literature. For the following, we will use a simple scheme for such a generator, which will facilitate the analysis.
The generator is described with the help of Figure 3. A closed conductor consisting of four plane segments with the sides a, l 0 and b is surrounded by a high explosive to be detonated at the left side. A magnetic flux to be trapped inside the rectilinear cavity is compressed by the collapse of the two opposite sides of the cavity with length l 0, forming two sides of a collapsing liner. After the magnetic field has reached a critical value, the end plate at the right side of the cavity will be blown out and the high electric current is suddenly switched onto the load R, which is our laser rod. An initial magnetic field H0 that is perpendicular to the drawn cut of Figure 3 is applied prior to the ignition of the explosive. This initial magnetic field for example, can be generated by discharging a capacitor bank over the conductor loop, as indicated. Conservation of magnetic flux then requires that
where l 1 is the distance of the collapsed liner from the endplate prior to the moment, that endplate is blown out by the magnetic pressure. Hm is the maximum magnetic field hence
From Maxwell ‘s equation
follows
where I is the total current in amps. From Eq. (17) follows for the maximum attainable current
Therefore, also
Assume for example l 0 = 100 cm, l 1 = 10 cm, b = l 1 = 10 cm, I0 = 3 × 106 A. It follows Im = 3 × 107 A, H0 = 3 × 105 gauss, and Hm = 3 × 106 gauss. The latter value of the attainable magnetic field agrees with experimentally obtained fields generated by explosive flux compression devices. A current of 3 × 106 A resulting in a magnetic field of 3 × 105 gauss is obtainable with a large capacitor bank. However, it seems to be alternatively possible to generate an initial magnetic field of H0 = 2 × 105 gauss with superconducting field coils.

Fig. 3. Explosively driven high current generator - Plane cut. The “Depth” of the device shown is equal to b.
The total magnetic energy prior to the flux compression is given by
and after the compression has taken place
hence

For the chosen example l 0 = 102 cm, l 1 = b = 10 cm, H0 =3 ×105 gauss it follows E0 = 4 × 1013 erg = 4 MJ, and E1 = 40 MJ. This energy is, therefore, of the right order of magnitude required for our purpose.
The voltage of the system is derived from (in electrostatic units)
where τ is the blow out time of the endplate. Blow out occurs at H = Hm and from the magnetic pressure acting on the endplate follows the speed by which the plate is blown off, by equating the kinetic energy density of the endplate material with the magnetic energy density:
hence
where ρ is the density of the endplate material. For Hm = 3 × 105 gauss and ρ ≈ 10 gm/cm3 one has v ≈ 3 × 105 cm/s. The time for blow out is about ![]() Since
Since ![]() it follows
it follows
For a = 10 cm, it follows V = 3 × 102 esu ≈105 volt. The total energy to be delivered is
But since (in electrostatic units) Im = bc Hm / 4π it follows E = ab l 1 (Hm2 / 4π), which is on the same order as E1, really a result that is consistent with the made assumptions. Because the voltage of 105 volt is not large enough to cause breakdown in liquid Argon, it is necessary to start the discharge by means of a number of conducting filaments embedded inside the liquid Argon.
4.3. The third method
In the third method, it is proposed to achieve the high population inversion by a chemical reaction-taking place in the laser material. A possible candidate for such a chemical laser may be a mixture of liquid chlorine and hydrogen. A more potent device may be a mixture of liquid fluorine and hydrogen at very low temperatures. Both reactions, the chlorine-hydrogen or the fluorine-hydrogen can be triggered almost simultaneously throughout the whole material, by the pulsed irradiation with an intense light source of short pulse width that is by the flash of another laser, preferably with a Q-switch.
The laser lines for most chemical lasers will be in the infrared that is opposed to our desire for a short wave length. A more serious obstacle may be the blocking of the laser transition due to a substantial population of the lower maser level at the elevated temperature resulting from the chemical reaction. Because of insufficient data, it seems that at this time no conclusion can be drawn.
5. THE ARRANGEMENT OF LASER AND THERMONUCLEAR MATERIAL
After the laser material has been energized, the laser can be triggered according to the principle of the laser amplifier. The principle of the idea is shown in Figure 4. For this purpose, the light pulse of a Q-switched gas laser, consisting of the same laser material as the dense rod, is directed onto the left end boundary of the high-energy high-density laser rod. If the Q-switched gas laser releases a pulse of sufficient intensity, the activated material in the high-density laser will be depopulated in one run by a light wave going to the right and increasing exponentially. The resulting laser beam is then focused onto the thermonuclear material by an optical lens. The method promises very short power pulses consistent with the condition that the energy should be deposited in about 10 ns or shorter.

Fig. 4. Arrangement of laser amplifier for the irradiation of the thermonuclear material.
It was pointed out above that the smallness of the volume to be irradiated may necessitate a magnetic reduction of the electronic heat conduction losses, requiring magnetic fields on the order of mega gauss. It is obvious that this can be done by the explosive generation of mega gauss fields such as in the high current generators.
6. APPLICATIONS
Since both the convergent shock wave approach and the high current generator approach are expected to have efficiencies of only a few percent and because of inefficient laser operation at l0%, energy inputs in excess of 104 MJ seem to be required, which correspond to an explosive charge in excess of one ton. These charges seem to be too large in size to be of any interest for military applications where they would have to compete with fission triggers in the kilogram range. The primary significance of the laser bomb seems to be in the Plowshare field where the size of the trigger is of minor significance, but where great emphasis is based on “cleanliness” of the nuclear charge. A second application may be an Orion-type nuclear pulse rocket propulsion scheme where the cleanliness of the nuclear charge is also regarded of certain importance.
7. CONCLUSION
The estimates presented in this paper demonstrate that the idea of a laser-triggered hydrogen bomb cannot be rejected off-hand. The estimates, however, also indicate that the technical problems which have to be solved are considerable, provided one of the proposed physical mechanisms for a large population inversion will turn out to be feasible. It seems to be a fortunate fact that the required trigger will become too large excluding the device from military applications.








