1. INTRODUCTION
In recent years, there has been considerable interest in conducting
laser-plasma experiments of relevance to astrophysical research. Results
from these experiments can be used to study fundamental physics, as well
as benchmark astrophysical codes. The FLASH code is one such astrophysics
code, produced at the University of Chicago under the accelerated
strategic computing initiative (ASCI), which is being used to study
laser-produced astrophysics experiments, as in Calder et al.
(2002). Blast waves are just one type of
laser-plasma experiment of astrophysical interest, which was conducted at
a variety of laboratories and simulated with a variety of numerical codes,
including Grun et al. (2003), Zhang
et al. (2003), and Peng et al.
(2003), among many others. Similarly, a blast
wave was produced at the Institute of Laser Engineering (ILE) of Osaka
University using a high-power laser to irradiate a planar plastic target
in a background nitrogen gas. In the present study, the FLASH code will be
used in an attempt to simulate this experiment. One problem is
ascertaining the initial conditions to input into FLASH since this code
does not model laser-solid interactions, but rather has sophisticated
modules to simulate the high-temperature, high-speed flow generated by the
laser source. Thus, a simplified model for intense laser irradiation of
planar targets will be used to estimate initial conditions. No attempt
will be made to improve or add physics modules to FLASH. This study will
analyze how well the current version of FLASH can simulate the
experimental blast wave.
2. EXPERIMENT
One beam of the ILE GEKKO XII laser system is used to irradiate a
plastic planar target. The beam impinged the target at an angle of
20°. The laser had a wavelength 1.053 μm, a pulse length of 1 ps,
energy of 7.7 J on target, and the optical f/# was 3.8. The laser
spot size on target was about 50 μm diameter. Thus, the on target
intensity was approximately 1017 W/cm2 at a
power of 8 × 1012 W. The plastic (polystyrene, CH) target
had a solid density of 1.06 g/cm3, a thickness of 6 μm,
and an average atomic weight of Z = 3.5. The vacuum chamber
containing the CH target was maintained at a pressure of 5 Torr ambient
nitrogen.
One of GEKKO's other laser beams (4ω, λ = 0.26 μm,
100 ps) was used to probe the blast wave trajectory. The probed CH target
was imaged by a knife-edge to a CCD camera such that the camera is looking
edge-on to the target (Schlieren technique). The blast wave was imaged at
16 ns after the laser pulse using with the CCD camera, as shown in Figure 1. The pixel resolution is approximately 12
μm. This image shows regions of relatively high density, such as
immediately behind the blast wave shock front. Note that the laser pulse
must pass through the background nitrogen gas to reach the target, which
causes a cylindrical blast wave in the nitrogen gas. This can be seen in
Figure 1 where the radial shock is intersecting
the spherical blast wave.
Blast wave from CH target at 16 ns using laser intensity of
1017 W/cm2 and power of 8 ×
1012 W.
From Figure 1, the size of the high-density
region adjacent to the spherical shock front is about 2.5 mm radius at 16
ns. Also, note the high-density structures within the blast wave. An
unavoidable laser pre-pulse 10−6 to 10−7
less power than the main pulse will interact with the CH target and
ambient nitrogen gas for approximately 1 ns before the main pulse arrives.
This pre-pulse will initiate plasma near the CH target and may dissociate
and ionize the nitrogen gas molecules.
3. THEORY
An analytic solution for a blast wave resulting from an instantaneous
energy release from a point source was solved by Sedov (1993). A self-similar solution is obtained for the
blast shock wave radius for both cylindrical and spherical waves, as given
by Zel'dovich and Raizer (1967) and Landau
and Lifshitz (1987)
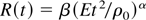
where E is the instantaneous energy deposition, t is
time; ρ0 is the ambient gas density in front of the shock
wave. The exponent α = 1/5 for spherical waves, and α =
1/4 for cylindrical waves. The constant β depends on the
polytropic coefficient γ, and is nearly 1.0 for typical gases.
This theory is valid for polytropic gases at times much longer than
the laser pulse length (1 ps), and for distances not too distant from the
source where the blast wave is still strong (i.e., ρ1
/ρ0 ∼ (γ + 1)/(γ − 1) where
ρ1 is the shocked density). Also, this theory assumes only
one gas with a point source (or line source for cylindrical waves)
releasing energy instantaneously. In the present experiment, the
“point source” is actually a disk of CH, and the expanding hot
CH plasma acts as a piston to initiate the strong shock into the
background nitrogen gas. Thus the theory given by Eq. (1) may not be
precisely correct for the present experiment. Indeed, from the FLASH
simulations significant amounts of CH are found in the high-density layer
near the shock front, not just shocked nitrogen. However, at later times
the 50 μm laser spot size is much smaller than the blast wave radius
such that the laser spot can be considered a point source and Eq. (1)
serves as a useful tool in analyzing the temperature effects of the
experiment.
At high laser intensities, such as the 1017
W/cm2 involved here, both “cold” and
“hot” electrons will be generated. The resulting plasma thus
has two species of electrons, each with a Maxwellian distribution. Typical
cold temperatures are on the order of 100–1000 eV, while hot
electron temperatures will be on the order of 10's of keV. From
experimental data at the high laser intensity of the present experiment,
the hot electron temperature, Th, is
approximated by Eliezer (2002)
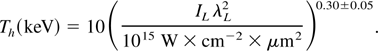
Thus, for the present experiment Th ∼
40 keV. The relative abundance of hot electrons to cold electrons is
approximated to be less than 10% at the present laser intensity and angle
of laser incidence. Unfortunately, FLASH only allows one temperature, thus
neglecting the effect of hot electrons and assuming ion and electron
equilibrium.
4. FLASH CODE
FLASH is a modular simulation code capable of handling general
compressible flow problems. Adaptive mesh refinement (AMR) is typically
used, but a uniform grid can be chosen instead. Supported geometry
selections are one-dimensional (1D) spherical, 2D axisymmetric
cylindrical, and three-dimensional (3D) Cartesian. The user defines a
problem through setting up initial conditions into the mesh domain,
including boundary type (i.e., reflecting, outflow, etc.), and then
chooses needed physics modules through a simple configuration file.
Hydrodynamic modules include the piecewise-parabolic method (PPM) scheme,
a Kurganov scheme, and a magnetohydrodynamics (MHD) module. As stated
before, the MHD module allows only one temperature. A variety of materials
can be used, but to be able to use radiative cooling or ionization and
recombination physics modules, only protons (H atoms), electrons, He, C,
N, O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni are available. Other available
physics modules include several equations of state (EOS) schemes, nuclear
burning, source heating, stirring, gravity, and different options for
conductivity and viscosity. FLASH uses the configuration file containing
the selected physics modules to automatically select and compile necessary
and interdependent lines of code. Note there are no non-physical
parameters to alter to force a desired solution (e.g., no flux
limiters).
4.1. Radiative cooling
In the hot CH region, the particle number densities are high such that
the CH plasma is optically thick. In this region, radiative loss is
therefore not significant, but radiative hydrodynamics could be important.
Unfortunately, FLASH does not include radiative transfer in the
hydrodynamics modules. The hot nitrogen gas region, which is heated by the
CH-originated shock wave (with Spitzer-Harm conductivity turned off) or
thermal wave (with Spitzer-Harm turned on), is of low enough density as to
be optically thin. Radiative loss in this hot nitrogen gas region is
therefore possible, but as will be described below is insignificant to the
flow development.
The internal energy εint (erg/g) of the fluid is
defined by FLASH as
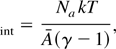
where Na is Avogadro's Number,
k is Boltzmann's constant, A is the average
atomic mass for the fluid, and γ is the ideal gas adiabatic index. For
diatomic nitrogen, A = 28 and γ = 1.4, and temperatures in
the hot nitrogen gas region are on the order of 107 °K.
Thus, the internal energy of the hot nitrogen gas is of the order of
1014 erg/g. Radiative cooling
is given by
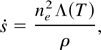
where ne is the electron density, ρ
is the fluid density, and Λ(T) is an empirical cooling
function available in Raymond et al. (1976). For the temperatures of interest, the best case
scenario is Λ(T) ∼ 10−22 erg ×
cm3/s. Assuming again a best case scenario of full
ionization, ne =
Zni =
ZρNa /A where
Z is the ionization state (seven for fully ionized N).
Mass density in the hot nitrogen region is about 3 ×
10−5 g/cm3, resulting in
.
A characteristic time of the flow needs to be multiplied by
to compare with the internal energy εint. Another way to
look at this is to calculate the time scale in which radiative cooling
would be important, such as
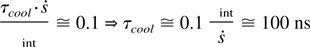
This very large time scale for radiative cooling is well past the
experiment time scale, and thus radiative cooling is not important in this
experiment.
4.2. Dissociation and ionization
As stated previously, FLASH can calculate electronic ionization and
recombination of C, N, and H atoms. However, no consideration is made for
diatomic molecules. The question of whether N2 is fully
dissociated is critical to the simulation, both to be able to apply the
ionization physics module and to use the correct background pressure for
the blast wave. The pressure gradient is the only forcing term in the
momentum equation, and the background pressure would double if
N2 is fully dissociated, which therefore would affect the
propagation of the blast wave.
Several studies of similar blast wave experiments in a nitrogen
background gas were published by MacFarlane et al. (1989), Giuliani et al. (1989), Laming and Grun (2002), and Laville et al. (2004). However, there is no consensus regarding the
state of the nitrogen. From MacFarlane et al. (1989), the density of diatomic nitrogen was used in
the simulation, although they noted that prompt X-rays from the
laser-plasma interaction would heat the background gas to 1–2 eV
(Ali & McLean, 1985). At these temperatures,
nitrogen would be completely dissociated, and partially ionized. However,
even if this heat bath were instantly available, it would take time to
dissociate. Laming and Grun (2002) assume
instant complete dissociation, and Laville et al. (2004) account for dissociation in the shock front.
Note that none of these simulations were done in full 2D axisymmetric
geometry.
The time scale for dissociation can be approximated through the
dissociation reaction rate kf
(cm3/mole × s)
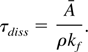
Reaction rates for high temperature nitrogen can be found in many
sources, including Dunn and Kang (1973). The
reaction rates for collisions between diatomic molecules (N2 +
N2) and diatomic and atomic nitrogen (N2 + N) are
given by
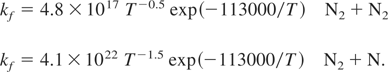
For 2 eV (2.3 × 104°K), kf = 2.4 × 1013 cm3/mole × s
(N2 + N2) and kf = 8.9
× 1013 cm3/mole × s (N2 +
N). For ambient diatomic nitrogen at 5 Torr, the density is 8 ×
10−6 g/cm3 and the dissociation time scale
is thus
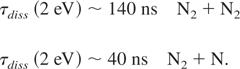
In either case, at temperatures of 2 eV a relatively long time
compared to the hydrodynamic time scale is required to dissociate the
diatomic nitrogen. Instantaneous dissociation is therefore not justified.
This same time scaling can be applied in the hot nitrogen region after
shock or thermal wave passage, where the temperature is on the order of
107°K (∼1 keV) and the density is 3 ×
10−5 g/cm3
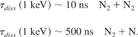
All of these time scales are on the order or larger than the entire
experiment. Of course, electron and ion collisions with diatomic molecules
have not been considered, which would accelerate dissociation. The point
here is that instantaneous dissociation is likely not appropriate, and
FLASH cannot account for dissociation effects. Further, since FLASH cannot
account for diatomic nitrogen in its ionization physics package, we also
cannot use the electronic ionization/recombination module in the
present simulations.
Even though ionization cannot be handled by FLASH in this case due to
the presence of diatomic nitrogen, an estimate of the typical ionization
time scale is useful, as given by Post et al. (1977)
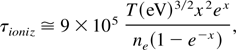
where x is the ionization potential I divided by
temperature (x = I/T). Note T is
in eV in this equation. The first ionization potential for atomic nitrogen
is 13 eV, and the electron density in the hot nitrogen region (singly
ionized) is ∼ 1018 cm−3 at a temperature
of 1 keV, which results in τioniz ∼ 0.4 ns.
The time scale for hydrodynamic flow is similar to this
τioniz time scale, and thus ionization could be
important to flow dynamics. However, MacFarlane et al. (1989) noted that ionization affects the fluid flow
only at early times very close to the laser spot, and classical
collisional hydrodynamics appears to be adequate to model the blast wave
evolution after initial time scales.
4.3. Single fluid temperature
FLASH only allows for one temperature, thus always assuming ion and
electron temperature equilibrium. In the hot CH region where the densities
are high, this may be a valid assumption. However, in the low-density hot
nitrogen region, the ion and electron temperatures likely are not in
equilibrium. Since this region includes unknown quantities of diatomic
nitrogen and various degrees of atomic nitrogen ionization, a time scale
calculation for temperature equilibration is difficult. Since a single
temperature is only available in FLASH, we cannot comment on the error
caused in the simulation due to ion and electron non-equilibrium effects.
However, Giuliani et al. (1989) did
follow both ion and electron temperatures in a similar experiment, and the
temperatures appear to be generally similar and in near equilibrium,
especially in the blast front region.
5. RESULTS
For the present FLASH simulation, a 2D axisymmetric cylindrical
geometry is used with the AMR scheme. FLASH version 2.4 is used. Since
magnetic fields are not considered, the MHD module is not used and the
hydrodynamic PPM scheme is used instead. The domain size is 3,000 ×
3,000 μm in the radial (r) and axial (z)
coordinates, with the minimum mesh size being under 0.1 μm in the CH
target, which is only 1 μm half-thickness at z = 0 (total
number of meshes ∼ 64000). The z = 0 and r = 0
boundaries are reflecting, while the z = 0.3 cm and r =
0.3 cm boundaries are outflows. Having a reflecting boundary at the
z = 0 location assures a zero velocity at this point. Otherwise,
unphysical high velocities occur at z = 0. A perfect gas equation
of state was assumed for all fluids.
FLASH was run with ionization/recombination and radiative cooling
not included, as discussed above. Spitzer-Härm conductivity, given by
σSH = 9.2 ×
10−7T(°K)5/2 in cgs units,
was either turned on or off in the simulations. Spitzer-Härm
conductivity was initially turned off to run a faster simulation since the
automatically calculated time step of the simulation is inversely
proportional to the conductivity. Thus, using σSH
results in a very small time step (Δt ∼
T−5/2) due to the high temperature of the
CH, whereas turning Spitzer-Härm off results in a time step several
orders of magnitude larger than Spitzer-Härm on case. For example, a
typical 2D simulation with Spitzer-Härm off required 2–3 days,
but with Spitzer-Härm on required over a month to complete. An Intel
Itanium 2 (900 MHz) processor-based Hewlett-Packard workstation was used
for these simulations.
Because FLASH is run in 2D, the initial temperature condition of the
CH was also assumed to be 2D. Therefore, a Gaussian temperature profile
was used for the initial temperature (or equivalently pressure) source,
given by
where r0 = 25 μm corresponding to a laser spot
diameter of approximately 50 μm, and T0 = 120 eV.
The source temperature of 120 eV was decided from 1D simulation using the
Osaka University ILESTA code, which includes laser absorption, ionization
and recombination, and relevant EOS physics. Because only basic
hydrodynamics, with Spitzer-Härm turned on or off, is used in the
present 2D FLASH simulations, the effect of higher or lower
T0 would only change the length scales of the flow,
resulting in similar flow morphologies.
According to Ditmire et al. (1996),
at the high laser power and intensity of the present experiment, a very
high speed radiative heat wave will propagate into the plastic upon laser
illumination. The time scale for propagating through the entire 6 μm
thickness of the plastic target is estimated to be ∼1 ps. Thus, it is
assumed the plastic target is instantly heated to the initial temperature
profile given by Eq. (11). Also, the entire slab of CH will not be ablated
and accelerated into the nitrogen background, but rather a small part of
the CH disk will move into the background gas at a characteristic speed of
∼2 × 107 cm/s. From 1D FLASH simulation, an
ablated CH thickness of 1 μm (or less) should be sufficient to
initiate a blast wave relevant to the Figure 1
results.
Shown in Figures 2 and 3 are 2D snapshots of density and temperature for
Spitzer-Härm conductivity on and off at an early time of 500 ps after
laser illumination. As can be seen from Figure
2, the density profiles are quite similar, but the temperature
profiles of Figure 3 are very different due to
the rapid propagation of a thermal wave resulting from Spitzer-Härm
conductivity being included. This Spitzer-Härm thermal wave results
in an isothermal temperature of ∼105°K behind the wave.
The hot CH must then propagate into this high temperature and high
pressure nitrogen background. However, this did not cause significant
differences in overall wave front propagation between the
Spitzer-Härm on and off cases later in time.
Density plots (log g/cm3) at 500 ps for (a)
Spitzer-Härm OFF and (b) Spitzer-Härm ON.
Temperature plots (°K) at 500 ps for (a)
Spitzer-Härm OFF and (b) Spitzer-Härm ON.
Shown in Figure 4 are similar density and
temperature plots at 16 ns only for the Spitzer-Härm off case, which
is the same time as the experimental result of Figure
1. Note the strong differences between the Spitzer-Härm off
case and experiment at this late time. The simulation with
Spitzer-Härm on is not shown since the simulation could not finish
even after two months of calculating and repeated increases in the minimum
mesh size. However, at a time of 2.5 ns (not shown), the propagation
speeds are very similar, and the overall blast wave structure are fairly
similar for the Spitzer-Härm on and off cases. Therefore, we assume
the Spitzer-Härm on and off results at 16 ns will have similar blast
wave propagation distances, although the detailed wave structure may
differ.
Plots of Spitzer-Härm off case at 16 ns for (a) density
(log g/cm3) and (b) temperature
(°K).
Note that the 120 eV initial temperatures resulted in blast wave
propagation about half the size of the experiment. According to Eq. (1),
the extent of the blast wave should scale as T1/5.
Thus, for the blast wave radius to double in size, the temperature should
be increased by a factor of 32, which would correspond to
T0 ∼ 4 keV. It is possible for ion temperatures to
be this high, and as previously stated hot electron temperatures should be
about 40 keV. Significant physical interaction is likely between ions and
electrons at these very high temperatures, and also a likely strong effect
on the nitrogen gas close to the CH target. However, none of these
physical effects can be modeled by FLASH, even if assuming completely
dissociated and ionized materials.
6. CONCLUSIONS
2D FLASH simulations were run with Spitzer-Härm conductivity on
and off in an attempt to simulate a laser-produced blast wave.
Dissociation, ionization, recombination, and radiative cooling were not
included. An initial Gaussian temperature profile with
T0 = 120 eV and spot radius r0 =
25 μm was used assuming 1 μm thickness of the CH disk is ablated
into the background nitrogen gas. Evolution of the blast wave differs
slightly between the cases of Spitzer-Härm on and off, and neither
case matches well with experiment. Due to the high temperatures involved,
a thermal wave should be expected such that the Spitzer-Härm
conductivity on case is more likely. However, all interesting physics
occurring near the CH target and corresponding interaction with the
background diatomic nitrogen gas has not been considered. As most other
authors point out, blast wave evolution can probably be simulated using
simple collisional hydrodynamics at time scales much larger than the laser
pulse time. The problem is how to decide the appropriate initial
conditions to start FLASH after such complicated interactions have
subsided.
Again, the point of this study was to use FLASH as simply as possible,
without changing or adding physics packages, or tuning “knobs”
to achieve the desired result. All that was input to FLASH were basic
material properties and a simple Gaussian temperature initial source
profile. FLASH then automatically proceeds with little interaction
required from the user. In fact, the only manipulation done during the
simulation runs was to occasionally increase the minimum mesh size to
speed up the simulation (note the number of mesh blocks increases as the
blast evolves such that the minimum block size can be increased without
loss of resolution). It is the authors' view, all of whom are
experimentalists, that running a simulation should be done this way. A
turn-key simulation code such as FLASH would not be very useful if
multiple knobs must be tuned to achieve a desired result, which would
produce different results depending on each user. In this sense, we can
say the FLASH code stands on its own, with no tuning required, but
apparently its included physics packages are inadequate to correctly model
the high-temperature laser-produced blast wave of the present experiment.
Future work will focus on uncovering which significant physical effects
are responsible for the discrepancies between simulation and experiment,
and possibly adding magnetic fields to the initial conditions.
ACKNOWLEDGMENTS
The software used in this work was in part developed by the
DOE-supported ASCI Alliance Center for Astrophysical Thermonuclear Flashes
at the University of Chicago. The authors are also grateful to various
researchers at the ASCI FLASH center who offered advice on working with
the FLASH code.
