Introduction
Pair-ion plasmas consisting of the positive and negative charged particles of equal mass have attracted special attention in the recent years due to the exhibition of the new state of the matter with unique thermodynamic properties different from ordinary electron-ion plasmas. These plasmas are found in some astrophysical environments (Yu et al., Reference Yu, Shukla and Stenflo1986) such as in galactic nuclei. On the other hand, in the laboratory, some pair-ion plasmas such as positron–electron pair plasma is produced in large tokomaks and in the next generation laser–plasma interaction experiment. Moreover, several experimental efforts have been made to produce pure pair-ion plasmas (Zank and Greaves, Reference Zank and Greaves1995; Oohara and Hatakeyama, Reference Oohara and Hatakeyama2003; Oohara et al., Reference Oohara, Kuwabara and Hatakeyama2007). There are some different schemes for producing electron–positron pair plasma in the laboratory. The electron–positron pair plasma can be experimentally generated by injection of a low-energy electron beam into a positron plasma (Oohara and Hatakeyama, Reference Oohara and Hatakeyama2003). Moreover, according to the academic reports the electron–positron pair plasma is produced via the collision of a wakefield-accelerated electron beam with a multi-petawatt laser (Lobet et al., Reference Lobet, Davoine, d'Humières and Gremillet2017). In addition, the electron–positron plasmas with unique characteristics can be produced by using a compact laser-driven setup (Lobet et al., Reference Lobet, Ruyer, Debayle, d'Humières, Grech, Lemoine and Gremillet2015; Sarri et al., Reference Sarri, Poder, Cole, Schumaker, Piazza, Reville, Dzelzainis, Doria, Gizzi, Grittani and Kar2015; Gu et al., Reference Gu, Klimo, Weber and Korn2016; Ribeyre et al., Reference Ribeyre, d'Humières, Jansen, Jequier, Tikhonchuk and Lobet2016). Since the electron–positron pair plasma generation and maintenance are not easy for longer times due to annihilation, the study of the collective modes in pair-ion plasmas is done in the pair-ion fullerene plasma produced in the laboratory. Recently, making use of a preparation of pair fullerene populations consisting of ![]() $C_{60}^ + $ and
$C_{60}^ + $ and ![]() $C_{60}^ - $ in equal numbers, the pair-ion plasmas were created in the laboratory. In this regard, Oohara et al. (Reference Oohara, Date and Hatakeyama2005) presented a novel method to generate a pair-ion plasma consisting of only the positive and negative ions of equal mass, using fullerene. Since in the case of fullerene pair-ion plasmas the frequency range of the collective phenomena is limited to the low frequencies due to the massive ions, the light pair-ion plasmas generated in the high-frequency range are suitable for studying the novel collective phenomena. The best example is the parametric scattering of high power laser from these environments studied in the present work. In this regard, since hydrogen is the most fundamental element of the periodic table, the pair-ion hydrogen plasmas consisting of H +and H − ions (Oohara et al., Reference Oohara, Kuwabara and Hatakeyama2007) having small mass have been considered in this research. Hydrogen-containing plasmas can be found in a variety of environments including planetary ionospheres, interstellar media (Mendez et al., Reference Mendez, Gordillo-Vazquez, Herrero and Tanarro2006), and in different industrial processes (Darwiche et al., Reference Darwiche, Nikravech, Awamat, Morvan and Amouroux2007; Rico et al., Reference Rico, Hueso, Cotrino, Gallardo, Sarmiento, Brey and González-Elipe2009) such as surface cleaning and controlled fusion devices (Curran et al., Reference Curran, Hopkins, Vender and James2000). In these plasmas, the dissociative attachment of low energetic electron (0.75 eV) with an excited hydrogen molecule is the main process of the formation of negative hydrogen ion as
$C_{60}^ - $ in equal numbers, the pair-ion plasmas were created in the laboratory. In this regard, Oohara et al. (Reference Oohara, Date and Hatakeyama2005) presented a novel method to generate a pair-ion plasma consisting of only the positive and negative ions of equal mass, using fullerene. Since in the case of fullerene pair-ion plasmas the frequency range of the collective phenomena is limited to the low frequencies due to the massive ions, the light pair-ion plasmas generated in the high-frequency range are suitable for studying the novel collective phenomena. The best example is the parametric scattering of high power laser from these environments studied in the present work. In this regard, since hydrogen is the most fundamental element of the periodic table, the pair-ion hydrogen plasmas consisting of H +and H − ions (Oohara et al., Reference Oohara, Kuwabara and Hatakeyama2007) having small mass have been considered in this research. Hydrogen-containing plasmas can be found in a variety of environments including planetary ionospheres, interstellar media (Mendez et al., Reference Mendez, Gordillo-Vazquez, Herrero and Tanarro2006), and in different industrial processes (Darwiche et al., Reference Darwiche, Nikravech, Awamat, Morvan and Amouroux2007; Rico et al., Reference Rico, Hueso, Cotrino, Gallardo, Sarmiento, Brey and González-Elipe2009) such as surface cleaning and controlled fusion devices (Curran et al., Reference Curran, Hopkins, Vender and James2000). In these plasmas, the dissociative attachment of low energetic electron (0.75 eV) with an excited hydrogen molecule is the main process of the formation of negative hydrogen ion as
So far, a great deal of theoretical work has appeared on the pair-ion plasmas in the literature (Moslem et al., Reference Moslem, Kourakis and Shukla2007; Saleem et al., Reference Saleem, Shukla, Eliasson and Stenflo2008; Vranjes et al., Reference Vranjes, Petrovic, Pandey and Poedts2008; Khan et al., Reference Khan, Ilyas, Wazir and Ehsan2014). An analysis of waves and instabilities in the created pair-ion plasma has been presented by Vranjes et al. (Reference Vranjes, Petrovic, Pandey and Poedts2008). Moreover, the electrostatic modes propagating along the magnetic field lines in a fullerene pair-ion plasma and also the collective motion of pair-ion plasma in the range of high frequencies in a hydrogen pair-ion plasma were proposed as a reference by Mahmood et al. (Reference Mahmood, Ur-Rehman and Saleem2009). The space-time evolution of the cyclotron and upper hybrid modes of a warm pair-ion plasma has been studied in the presence of a constant magnetic field (Pramanik et al., Reference Pramanik, Maity and Chakrabarti2016). Recently, a number of scientists have been interested in studying the evolution of the linear and nonlinear electrostatic shocks in the pair-ion plasmas (Misra, Reference Misra2009; Masood and Rizvi Reference Masood and Rizvi2011, Reference Masood and Rizvi2012). Meanwhile, Thomson scattering of a pair-ion plasma interacting with an incident electromagnetic wave (EMW) in the collision and collisionless limits has been investigated by Jian (Reference Jian2006). Recently, a number of theoretical investigations have been focused on the phase-mixing phenomenon in the magnetized and un-magnetized pair-ion plasmas (Pramanik et al., Reference Pramanik, Maity and Chakrabarti2014, Reference Pramanik, Maity and Chakrabarti2015). In addition to above-mentioned works, the linear and nonlinear electrostatic waves were studied in impure pair-ion (pair-ion-electron) plasmas (Saleem et al., Reference Saleem, Shukla, Eliasson and Stenflo2008; Mahmood et al., Reference Mahmood, Ur-Rehman and Saleem2009). The presence of electrons in these systems has been discovered through observation of ion acoustic wave in recent experiments with fullerene plasmas. Also, as shown recently, the presence of electrons causes the electrostatic solitons to appear in the pair-ion plasma. The excitation of ion sound waves in a pair-ion plasma, through electron beam induced Cherenkov instability, has been also investigated (Ehsan et al., Reference Ehsan, Tsintsadze, Shah, Trines and Imran2016). Although various properties of the pair-ion and electron-pair-ion plasmas have been extensively investigated so far, to the best of our knowledge, the stimulated scatterings from these environments as well as the energy absorption of EMWs in these plasmas have not been addressed yet. So, the goal of the present paper is to study the laser scattering and absorption in both pure and impure hydrogen pair-ion plasmas.
In this paper, a developed fully kinetic electromagnetic particle-in-cell (PIC) simulation code (Mehdian et al., Reference Mehdian, Kargarian and Hajisharifi2015) has been employed to investigate the nonlinear interaction of high power laser with pure and impure hydrogen pair-ion plasmas in detail. For this purpose, the excited modes behavior in these plasmas in the interaction with an intense short-pulse laser relying on the nonlinear phenomena such as wave-breaking and phase-mixing has been studied, and the results have been compared with the behavior of an electron-hydrogen plasma. We have studied the nonlinear laser energy absorption in impure pair-ion plasma varying the electron density number. We have also shown in a characteristic range of plasma density a considerable amount of laser energy is transmitted to the plasma particles in the laser direction. Knowing how the energy of high power laser can be converted to the directed kinetic energy or thermal energy of the plasma particles is important in various applications including the laser fusion schemes, plasma-based particle acceleration, and high-energy electron production.
This paper is organized as follows: In the section ‘Modeling and simulation method’, the modeling and simulation used in the paper have been presented. In the section ‘Nonlinear plasma modes in the pure andimpure hydrogen pair-ion plasmas’, the phase-mixing phenomenon in both pure and impure hydrogen pair-ion plasmas has been spatiotemporally scrutinized. The section ‘Nonlinear laser absorption in pure and impure hydrogen pair-ion plasmas’ is devoted to the investigation of the laser energy absorption rate in the finite-size electron-ion plasma and pure and impure hydrogen pair-ion plasmas relying on the nonlinear phenomena related to the laser absorption. Finally, the conclusion is given in the section ‘Conclusion’.
Modeling and simulation method
A quantitative description of laser-driven electron acceleration requires numerical simulations. For this purpose, we now employ a relativistic electromagnetic 1D3V code to focus on the interaction of a short high-intensity laser pulse with the pure and impure hydrogen pair-ion plasmas consisting of the cold ions (T i ≪ eV) and the warm electron impurities (T e ~ eV). In the considered configuration, the cold-ion assumption (equivalently the condition of T i ≪ T e ~ eV) has been made to eliminate the heavily damp of the excited electrostatic waves in the system due to ion-landau damping phenomenon. For this purpose, these necessary conditions have been worked out in the considered system by typically choosing the ion temperature in the cold regime, T i = 10−3eV, and the electron temperature in the warm regime, T e = 10 eV. The other simulation parameters are as follows:
The plasma with a step-like density profile is located in the interval of ![]() $80{\kern 1pt} {\rm \mu m} \lt x \lt 200{\kern 1pt} {\rm \mu m}$ (simulation box with the length
$80{\kern 1pt} {\rm \mu m} \lt x \lt 200{\kern 1pt} {\rm \mu m}$ (simulation box with the length ![]() $250{\kern 1pt} {\rm \mu m}$). Simulation is carried out for a laser pulse with wavelength
$250{\kern 1pt} {\rm \mu m}$). Simulation is carried out for a laser pulse with wavelength ![]() ${\rm \lambda} _L = 1.6{\kern 1pt} {\rm \mu m}$, pulse duration τ = 50 fs, and intensity
${\rm \lambda} _L = 1.6{\kern 1pt} {\rm \mu m}$, pulse duration τ = 50 fs, and intensity ![]() $I = 2.14 \times 10^{18}{\kern 1pt} W/{\rm c}{\rm m}^2$ whose electric and magnetic field components are along the y and z directions, respectively.
$I = 2.14 \times 10^{18}{\kern 1pt} W/{\rm c}{\rm m}^2$ whose electric and magnetic field components are along the y and z directions, respectively.
This normally incident laser pulse has a Gaussian profile with the normalized peak amplitude a which is related to the laser intensity by ![]() $I = 1.37(a^2/{\rm \lambda} _L^2 ) \times 10^{18}\;{\rm W}/{\rm c}{\rm m}^2\,{\rm \mu} {\rm m}^2$. Forty-eight super-particles are used as per cell in the simulation box where the time and space steps have been chosen dt = 0.03 fsand δx = 0.01 μm, respectively. It is worth mentioning that all selected parameters used in this paper are normalized as τ = tω l, P x,y = p x,y/m ec,
$I = 1.37(a^2/{\rm \lambda} _L^2 ) \times 10^{18}\;{\rm W}/{\rm c}{\rm m}^2\,{\rm \mu} {\rm m}^2$. Forty-eight super-particles are used as per cell in the simulation box where the time and space steps have been chosen dt = 0.03 fsand δx = 0.01 μm, respectively. It is worth mentioning that all selected parameters used in this paper are normalized as τ = tω l, P x,y = p x,y/m ec, ![]() $E_{x,y} = {E}^{\prime}_{x,y}e/m_{\rm e}c{\rm \omega} _l$,
$E_{x,y} = {E}^{\prime}_{x,y}e/m_{\rm e}c{\rm \omega} _l$, ![]() $B_{x,y} = c{B}^{\prime}_{x,y}e/m_{\rm e}c{\rm \omega} _l$. Here, λl and ωl are laser wavelength and frequency, respectively.
$B_{x,y} = c{B}^{\prime}_{x,y}e/m_{\rm e}c{\rm \omega} _l$. Here, λl and ωl are laser wavelength and frequency, respectively.
Nonlinear plasma modes in the pure and impure hydrogen pair-ion plasmas
The interaction of short intense laser pulse with plasmas is a challenging area of applied physics including plasma heating (Honda et al., Reference Honda, Meyer-ter-Vehn and Pukhov2000), electron acceleration (Kumar et al., Reference Kumar, Pandey and Tripathi2010; Mehdian et al., Reference Mehdian, Kargarian and Hajisharifi2014a, Reference Mehdian, Kargarian, Hajisharifi and Hasanbeigi2014b), laser fusion (Klimo et al., Reference Klimo, Tikhonchuk, Ribeyre, Schurtz, Riconda, Weber and Limpouch2011; Yan et al., Reference Yan, Ren, Li, Maximov, Mori, Sheng and Tsung2012), and astrophysics laboratories (Farley et al., Reference Farley, Estabrook, Glendinning, Glenzer, Remington, Shigemori, Stone, Wallace, Zimmerman and Harte1999). The comprehensive concepts of this area of physics rely on a thorough understanding of nonlinear phenomena excited in the system, particularly phase mixing and wave breaking. We consider an ultra-intense laser pulse irradiated on a plasma. In this system, the nonlinear effects cause the excited electrostatic waves to become non-periodic and then wave-breaking process appears (Bulanov et al., Reference Bulanov, Yamagiwa, Esirkepov, Dylov, Kamenets, Knyazev, Koga, Kando, Ueshima, Saito and Wakabayashi2006). Physically, when the fluid speed along the crest of the wave exceeds the wave phase speed the wave-breaking amplitude is reached, consequently the wave starts to break (Modena et al., Reference Modena, Najmudin, Dangor and Clayton1995; Verma et al., Reference Verma, Sengupta and Kaw2012). A plasma wave can also break at an amplitude well below its wave-breaking amplitude via mixing of phases. This phenomenon is attributed to the space dependence of the wave characteristic frequency. In this state, the space dependency of the frequency causes the different oscillators (e.g., electrons) to oscillate with their local frequencies. As a result, the phase difference among the adjacent oscillators increases as time elapses and finally a moment comes when the neighboring oscillators’ trajectories start to cross one another, leading to a complete destruction in the wave structure and hence the phase-mixing phenomenon occurs (Sengupta et al., Reference Sengupta, Saxena, Kaw, Sen and Das2009; Sarkar et al., Reference Sarkar, Maity and Chakrabarti2013; Mehdian et al., Reference Mehdian, Kargarian and Hajisharifi2014a, Reference Mehdian, Kargarian, Hajisharifi and Hasanbeigi2014b). Signatures of phase-mixing have often been seen through the loss of periodicity of wave and through the appearance of density bursts. Moreover, other physical effects such as plasma inhomogeneity, relativistic mass variation, and motion of background massive ions have been recognized as possible sources of phase mixing phenomenon (Maity et al., Reference Maity, Chakrabarti and Sengupta2012; Kargarian et al., Reference Kargarian, Hajisharifi and Mehdian2016). Phase mixing or wave breaking phenomena of various normal modes of plasmas are being extensively reported in different plasma contexts theoretically. Recently, the phase mixing phenomenon has been theoretically studied by several authors in different plasma contexts including electron–positron plasmas (Maity et al., Reference Maity, Chakrabarti and Sengupta2013a, Reference Maity, Sarkar, Shukla and Chakrabarti2013b), multispecies electron–positron-ion plasmas (Maity, Reference Maity2014), and pair-ion plasmas (Pramanik et al., Reference Pramanik, Maity and Chakrabarti2015). Here, we investigate the phase-mixing of the excited electrostatic modes in a pure pair-ion plasma comprising negative- and positive-hydrogen ions and in an impure pair-ion plasma consisting of negative- and positive-hydrogen ions and electrons, using the mentioned simulation method in the previous section.
Here, in the following simulations, the positive ion number density (n i+) is obtained from n i+ = n H+n cr. where n H+ is a dimensionless constant value considered in the paper as n H+ = 0.1, 0.03, and n cr is the critical density related to the laser frequency, ωl, with the relation ![]() $n_{{\rm cr}} = \varepsilon _0m_{\rm e}{\rm \omega} _l^2 /e^2$. In these simulations
$n_{{\rm cr}} = \varepsilon _0m_{\rm e}{\rm \omega} _l^2 /e^2$. In these simulations ![]() ${\rm \omega} _l = 1.17 \times 10^{15}{\kern 1pt} {\rm s}^{ - 1}$ so the critical density becomes n cr = 0.42 × 1027 1/m3. Calculating the positive ion number density for each case from the above relation, the negative ion and electron number densities are obtained using the values n H-/nH+ = β and n el = (1 -β)n H+, respectively, where 0 ≤ β ≤ 1 is a constant value.
${\rm \omega} _l = 1.17 \times 10^{15}{\kern 1pt} {\rm s}^{ - 1}$ so the critical density becomes n cr = 0.42 × 1027 1/m3. Calculating the positive ion number density for each case from the above relation, the negative ion and electron number densities are obtained using the values n H-/nH+ = β and n el = (1 -β)n H+, respectively, where 0 ≤ β ≤ 1 is a constant value.
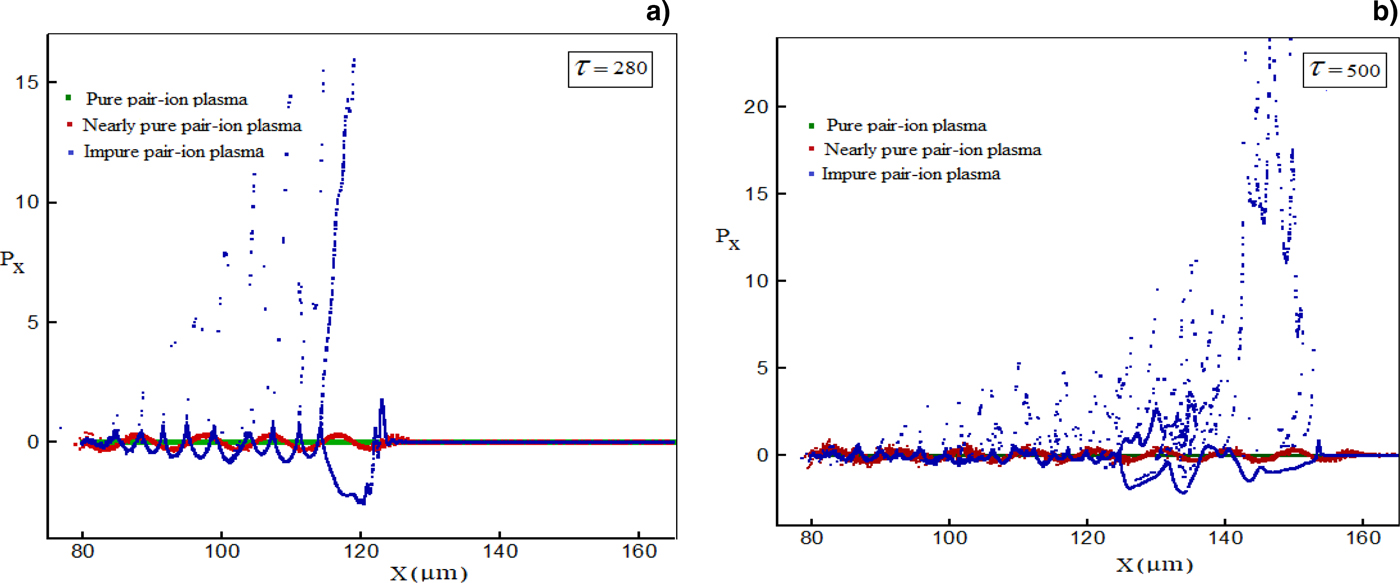
The simulation results of the longitudinal phase-space associated with the oscillation modes in highly pure (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$), nearly pure (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$), nearly pure (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.98$), and impure hydrogen pair-ion plasmas (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.98$), and impure hydrogen pair-ion plasmas (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.2$) with number density n H+ = 0.1 (n H+ is normalized to the critical density, n cr) and laser intensity a = 2 have been indicated in Figures 1a and 1b, respectively, for normalized times τ = 280 and τ = 500. One can see that in the impure pair-ion plasma, the excited oscillation modes have considerably lost their periodicity with time, signifying the wave-breaking and the mixing of phases. While, in the nearly pair-ion plasma (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.2$) with number density n H+ = 0.1 (n H+ is normalized to the critical density, n cr) and laser intensity a = 2 have been indicated in Figures 1a and 1b, respectively, for normalized times τ = 280 and τ = 500. One can see that in the impure pair-ion plasma, the excited oscillation modes have considerably lost their periodicity with time, signifying the wave-breaking and the mixing of phases. While, in the nearly pair-ion plasma (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} \to 1$) the excited oscillation modes with the small amplitude, preserve their form as sinusoidal by time lapse. This is because in the presence of considerable light negative species, namely electrons, in an impure pair-ion plasma, the mixing of the excited modes occurs at a shorter time. Moreover, as we expected, in the highly pure pair-ion plasma (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} \to 1$) the excited oscillation modes with the small amplitude, preserve their form as sinusoidal by time lapse. This is because in the presence of considerable light negative species, namely electrons, in an impure pair-ion plasma, the mixing of the excited modes occurs at a shorter time. Moreover, as we expected, in the highly pure pair-ion plasma (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$) there are no excited longitudinal oscillation modes in the system. As a result, for the fixed value of ion-positive number density, by increasing the ratio of the negative ion to positive ion density number, the phase-mixing time increases.
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$) there are no excited longitudinal oscillation modes in the system. As a result, for the fixed value of ion-positive number density, by increasing the ratio of the negative ion to positive ion density number, the phase-mixing time increases.
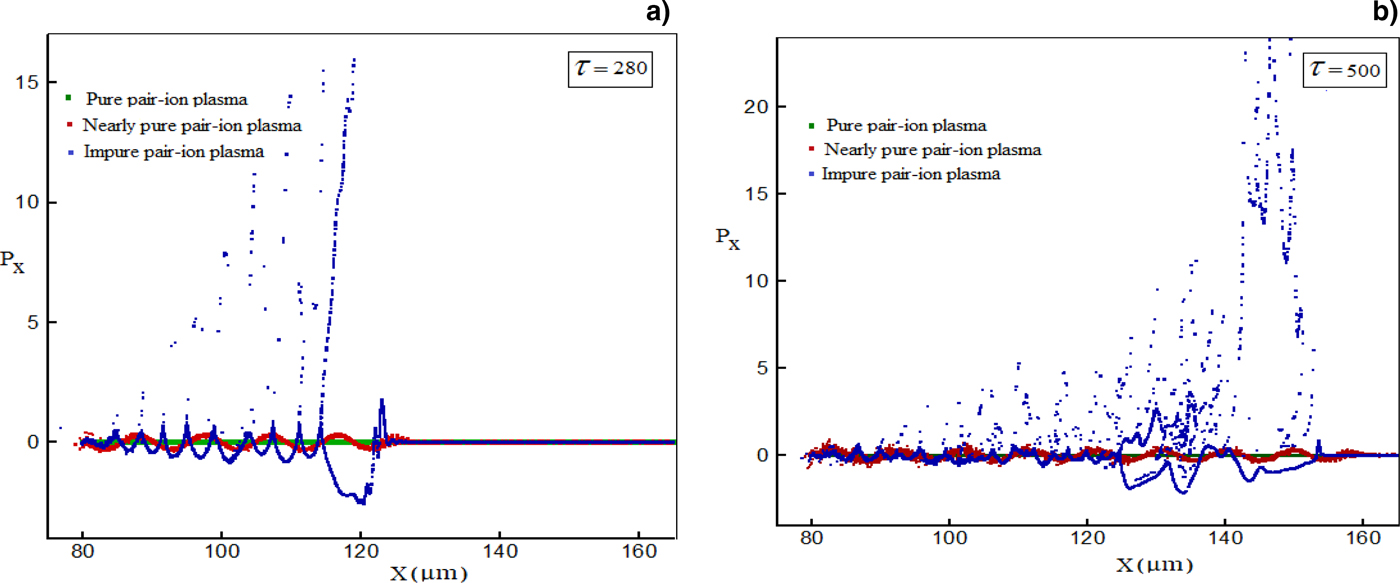
Fig. 1. Longitudinal phase-space associated with the oscillation modes in highly pure (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$, green plot), nearly pure (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$, green plot), nearly pure (![]() $n_{{\rm H}_ -} /n_{{\rm H}_{\rm +}} = 0.98$, red plot) and impure hydrogen pair-ion plasmas (
$n_{{\rm H}_ -} /n_{{\rm H}_{\rm +}} = 0.98$, red plot) and impure hydrogen pair-ion plasmas (![]() $n_{{\rm H}_ -} /n_{{\rm H}_{\rm +}} = 0.2$, blue plot) at two different times (a) τ = 280 and (b) τ = 500 with a = 2 and n H+ = 0.1.
$n_{{\rm H}_ -} /n_{{\rm H}_{\rm +}} = 0.2$, blue plot) at two different times (a) τ = 280 and (b) τ = 500 with a = 2 and n H+ = 0.1.
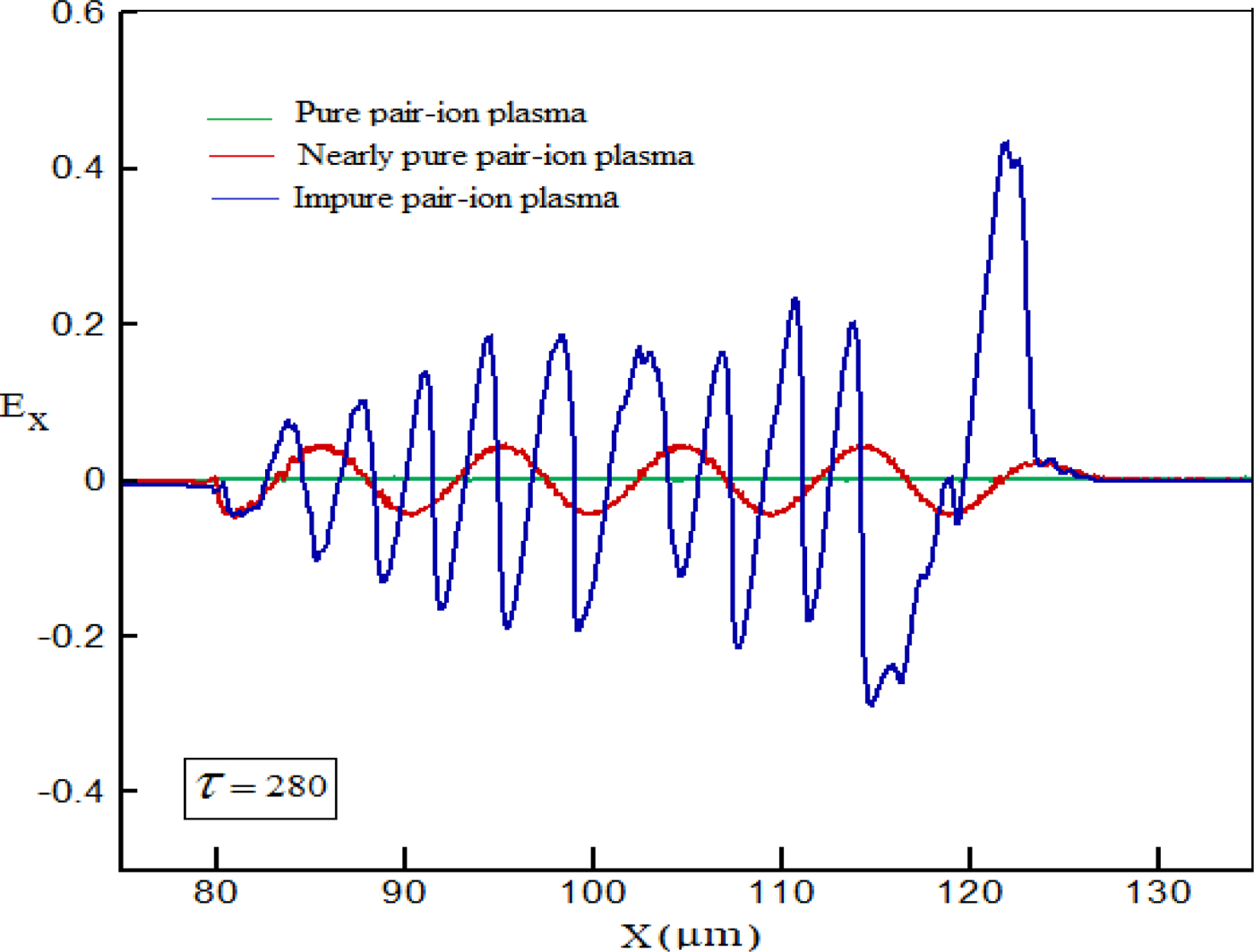
The spatiotemporal evolution of the electric field profile associated with the electrostatic oscillations in the phase-mixing region is illustrated in Figure 2. Here, E x component refers to the excited electrostatic modes in the system. This component arises due to the space-charge distribution of the plasma species namely electron, negative and positive hydrogen ions. As can be seen in this figure, in a highly pure pair-ion plasma (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$) an electrostatic field cannot be excited in the environment due to the approximately equal-mass of the two species while in a nearly pure pair-ion plasma (
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 1$) an electrostatic field cannot be excited in the environment due to the approximately equal-mass of the two species while in a nearly pure pair-ion plasma (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.98$) the weak wakefield with a regular electric field can be excited in the presence of electrons. Whereas, in the impure hydrogen pair-ion plasma with
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.98$) the weak wakefield with a regular electric field can be excited in the presence of electrons. Whereas, in the impure hydrogen pair-ion plasma with ![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.2$ the excited electric field profile is not regular anymore (non-sinusoidal profile) and the steepening and dips in the peaks of the profile in the phase-mixing region confirm that the wave breaking occurs at the shorter time for this plasma, comparing with the nearly pure pair-ion plasma.
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.2$ the excited electric field profile is not regular anymore (non-sinusoidal profile) and the steepening and dips in the peaks of the profile in the phase-mixing region confirm that the wave breaking occurs at the shorter time for this plasma, comparing with the nearly pure pair-ion plasma.
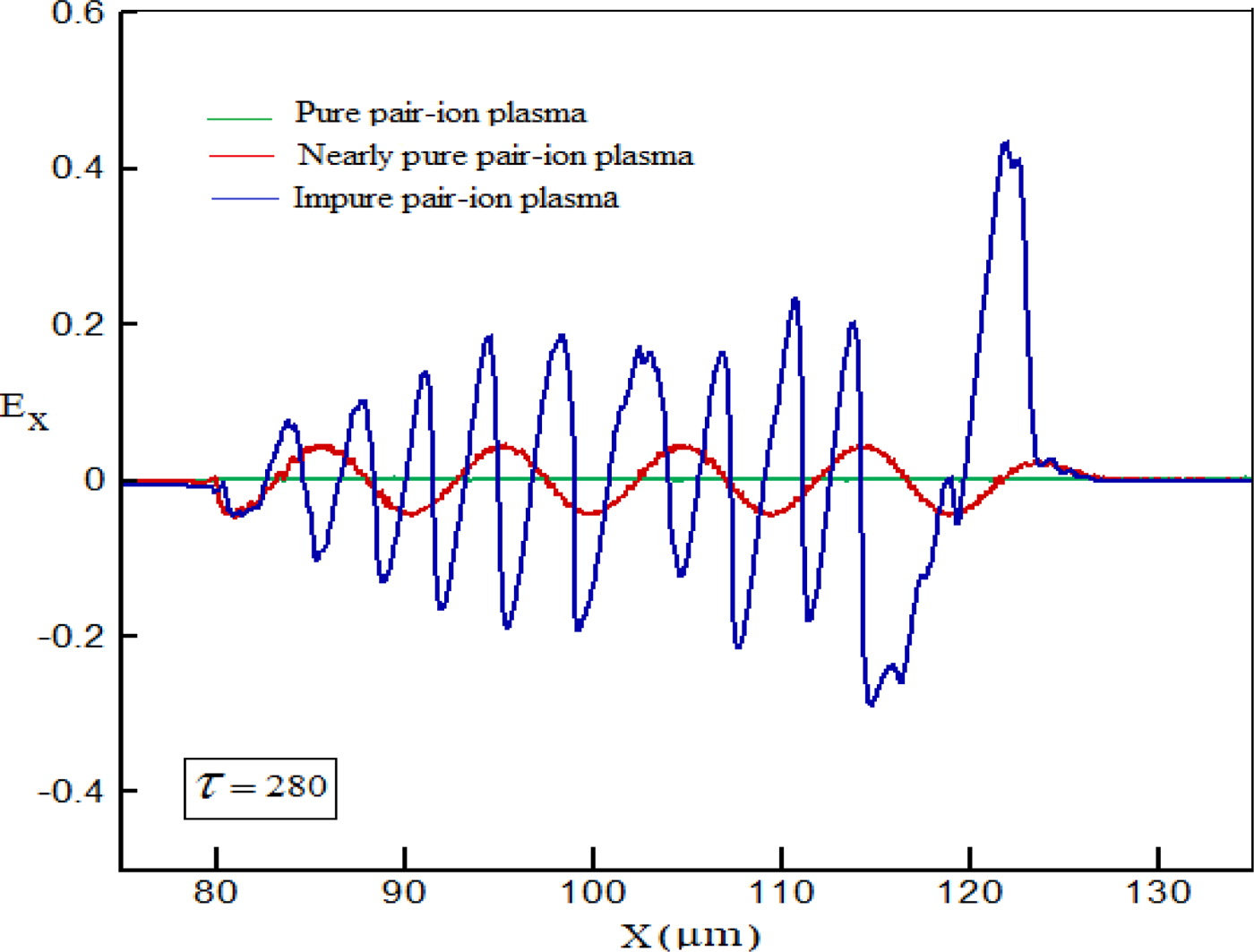
Fig. 2. Space-time evolution of normalized electric field associated with the excited electrostatic wave at τ = 280 for a highly pure (green line), nearly pure (red line), and impure (blue line) hydrogen pair- ion plasma with a = 2 and n H+ = 0.1.
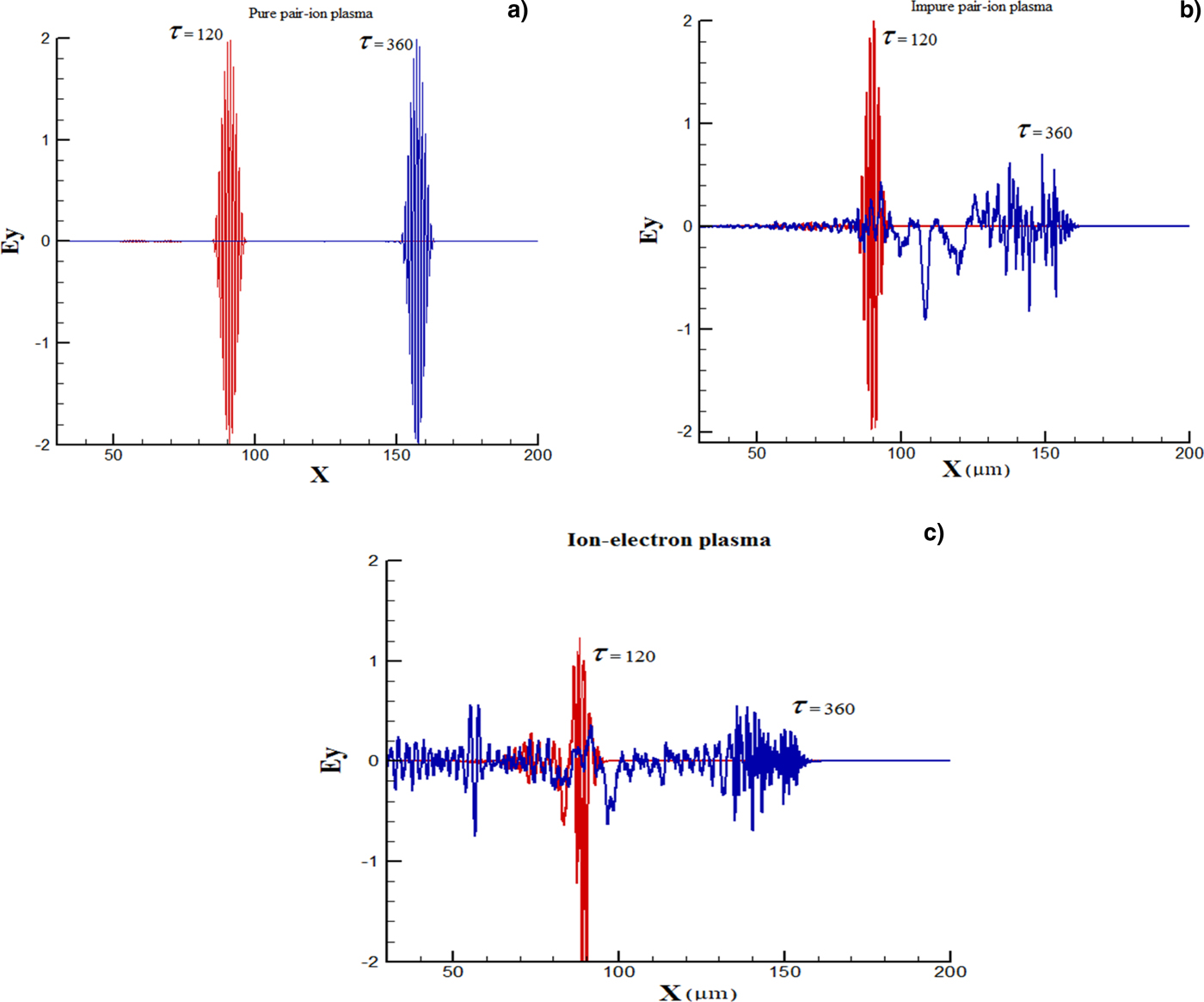
We close this section by an investigation into the laser scattering from the finite-size pure and impure pair-ion plasmas. For this purpose, the space evolution of the transverse electric field of high power laser, a = 2, interacting with the pure hydrogen pair-ion plasma, impure hydrogen pair-ion plasma, and ion-electron plasma at two different normalized times is illustrated in Figures 3a–3c. As can be clearly seen in these figures, in the interaction of laser with pure pair-ion plasma (Fig. 3a) the laser scattering is negligible and in this case, the laser passes through the medium without any considerable change. While, in the interaction with impure pair-ion plasma (Fig. 3b) at the presence of the electrons, an un-ignorable amount of laser light starts to leave the plasma environment in a long time due to the stimulated scattering. Figure 3c shows that in the interaction of laser with an ion-electron plasma, a significant amount of the scattered light leaves the plasma environment at τ = 360 and so cannot be absorbed any further by the plasma particles.
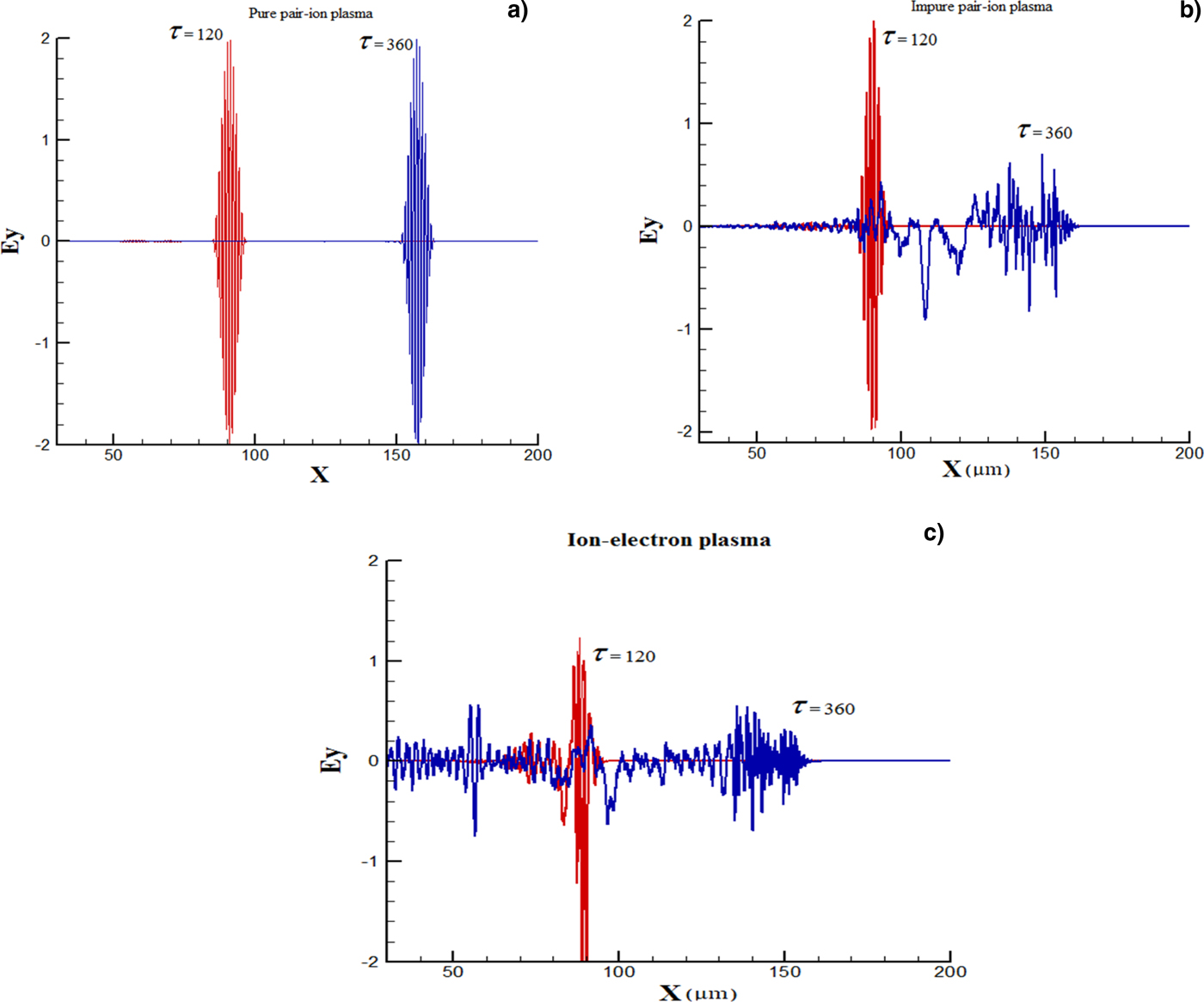
Fig. 3. Space evolution of the transverse electric field at two different times τ = 120 and τ = 360 in the interaction of laser pulse (a = 2) with (a) pure hydrogen pair-ion plasma, (b) impure hydrogen pair-ion plasma, and (c) ion-electron plasma. In these figures, the normalized positive hydrogen number density is n H+ = 0.1.
Nonlinear laser absorption in pure and impure hydrogen pair-ion plasmas
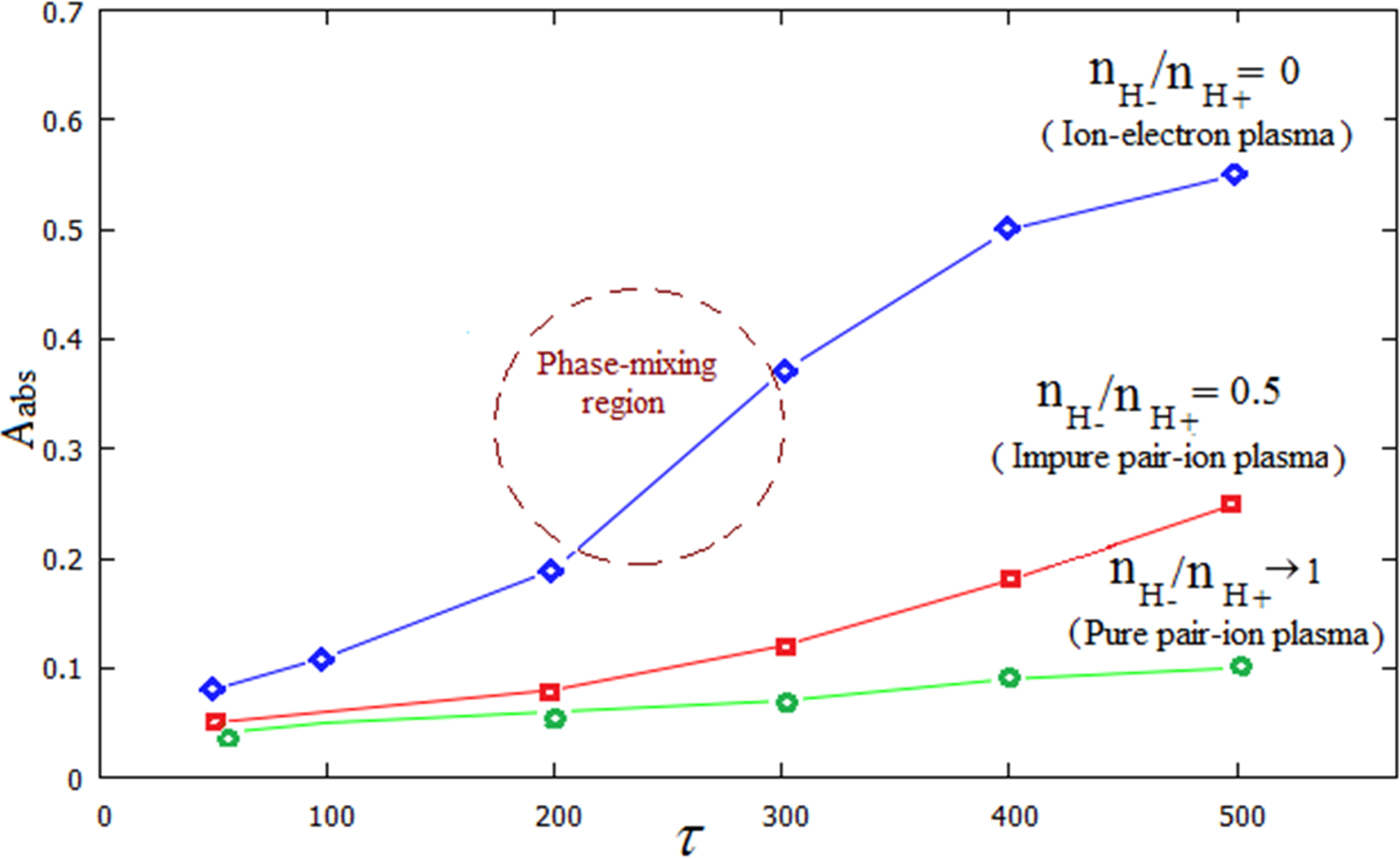
In the interaction of intense short-pulse laser with the finite-size plasma environment, there are some nonlinear phenomena that drastically affect the laser energy absorption rate by the plasma particles. Evidently, the phase-mixing or wave-breaking phenomenon described in the previous section has an important role in the plasma heating and particle energization (Maity et al., Reference Maity, Chakrabarti and Sengupta2013a, Reference Maity, Sarkar, Shukla and Chakrabarti2013b). In this section, we will show how these nonlinear phenomena have a substantial role in the conversion of laser energy to the directed kinetic or thermal energy of the charged plasma particles. For this purpose, using the obtained results in the previous section, the behavior of laser absorption rate (A abs = (W t − W t=0/W t=0) where ![]() $W_t = \sum\nolimits_{{\rm \alpha} = 1}^N {((\gamma _{\rm \alpha} - 1)m_{\rm \alpha} c^2)} $ is the kinetic energy of all species in each time step with N the total number of the particles, γα the relativistic factor, and W t=0 the initial kinetic energy of particles) in a finite-size nearly pure pair-ion plasma, impure pair-ion plasma, and ion-electron plasma versus normalized time (τ) for a = 2 and n H+ = 0.1 has been indicated in Figure 4 for a fixed value of the positive ion density. As can be seen in this figure, in the hydrogen ion-electron plasma (topmost curve) the absorption rate increases with time until saturation is reached. With increasing time some nonlinear phenomena such as laser scattering from the finite-size plasma are underway, therefore, a considerable amount of laser energy is reflected from the plasma environment (see Fig. 3c) and cannot be absorbed any further by the plasma particles, resulting in the saturation of energy absorption. Investigation of the absorption curve for such a plasma shows a steeper slope in the absorption curve when the wave-breaking or phase-mixing phenomenon occurs, as shown on the topmost curve, while the absorption curve related to the nearly pure pair-ion plasma (lowest curve) shows that the phase mixing has not yet occurred in this system at the considered time. The absorption curve of impure pair-ion plasma (
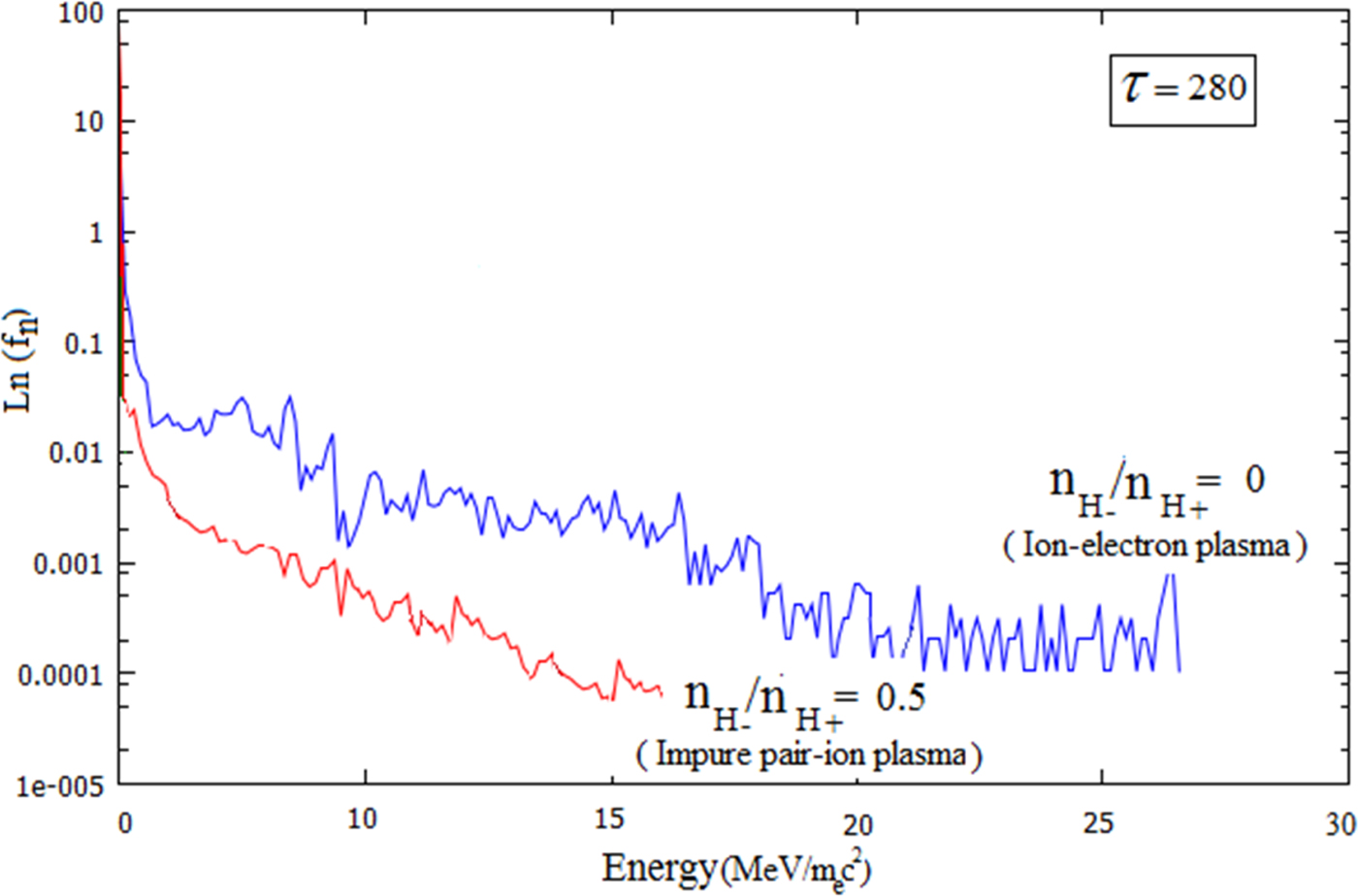
$W_t = \sum\nolimits_{{\rm \alpha} = 1}^N {((\gamma _{\rm \alpha} - 1)m_{\rm \alpha} c^2)} $ is the kinetic energy of all species in each time step with N the total number of the particles, γα the relativistic factor, and W t=0 the initial kinetic energy of particles) in a finite-size nearly pure pair-ion plasma, impure pair-ion plasma, and ion-electron plasma versus normalized time (τ) for a = 2 and n H+ = 0.1 has been indicated in Figure 4 for a fixed value of the positive ion density. As can be seen in this figure, in the hydrogen ion-electron plasma (topmost curve) the absorption rate increases with time until saturation is reached. With increasing time some nonlinear phenomena such as laser scattering from the finite-size plasma are underway, therefore, a considerable amount of laser energy is reflected from the plasma environment (see Fig. 3c) and cannot be absorbed any further by the plasma particles, resulting in the saturation of energy absorption. Investigation of the absorption curve for such a plasma shows a steeper slope in the absorption curve when the wave-breaking or phase-mixing phenomenon occurs, as shown on the topmost curve, while the absorption curve related to the nearly pure pair-ion plasma (lowest curve) shows that the phase mixing has not yet occurred in this system at the considered time. The absorption curve of impure pair-ion plasma (![]() $n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.5$) shows that the phase mixing just starts to occur at the maximum time. A comparison of the three curves illustrates that in a nearly pure pair-ion plasma, the least amount of laser energy is transferred to the plasma. This can be attributed to the absence of the considerable amount of electrons (compared with the two other plasmas) playing the essential role in the laser energy transition in this plasma. In other words, in a nearly pair-ion plasma the coupling between the excited modes and plasma particles is loose due to the weak electric field and low amplitude oscillation modes in this system. For the more precise investigation, the logarithmic spectrum of the electrons related to the impure pair-ion plasma and ion-electron hydrogen plasma at τ = 280 is shown in Figure 5. As can clearly be seen in this figure, the excited strong wakefield in these systems can accelerate the electrons to energies in the range of several MeV at τ = 280. Meanwhile, in the ion-electron plasma, the electrons obtain more energy than in the impure pair-ion plasma.
$n_{{\rm H}_ -} /n_{{\rm H}_ +} = 0.5$) shows that the phase mixing just starts to occur at the maximum time. A comparison of the three curves illustrates that in a nearly pure pair-ion plasma, the least amount of laser energy is transferred to the plasma. This can be attributed to the absence of the considerable amount of electrons (compared with the two other plasmas) playing the essential role in the laser energy transition in this plasma. In other words, in a nearly pair-ion plasma the coupling between the excited modes and plasma particles is loose due to the weak electric field and low amplitude oscillation modes in this system. For the more precise investigation, the logarithmic spectrum of the electrons related to the impure pair-ion plasma and ion-electron hydrogen plasma at τ = 280 is shown in Figure 5. As can clearly be seen in this figure, the excited strong wakefield in these systems can accelerate the electrons to energies in the range of several MeV at τ = 280. Meanwhile, in the ion-electron plasma, the electrons obtain more energy than in the impure pair-ion plasma.
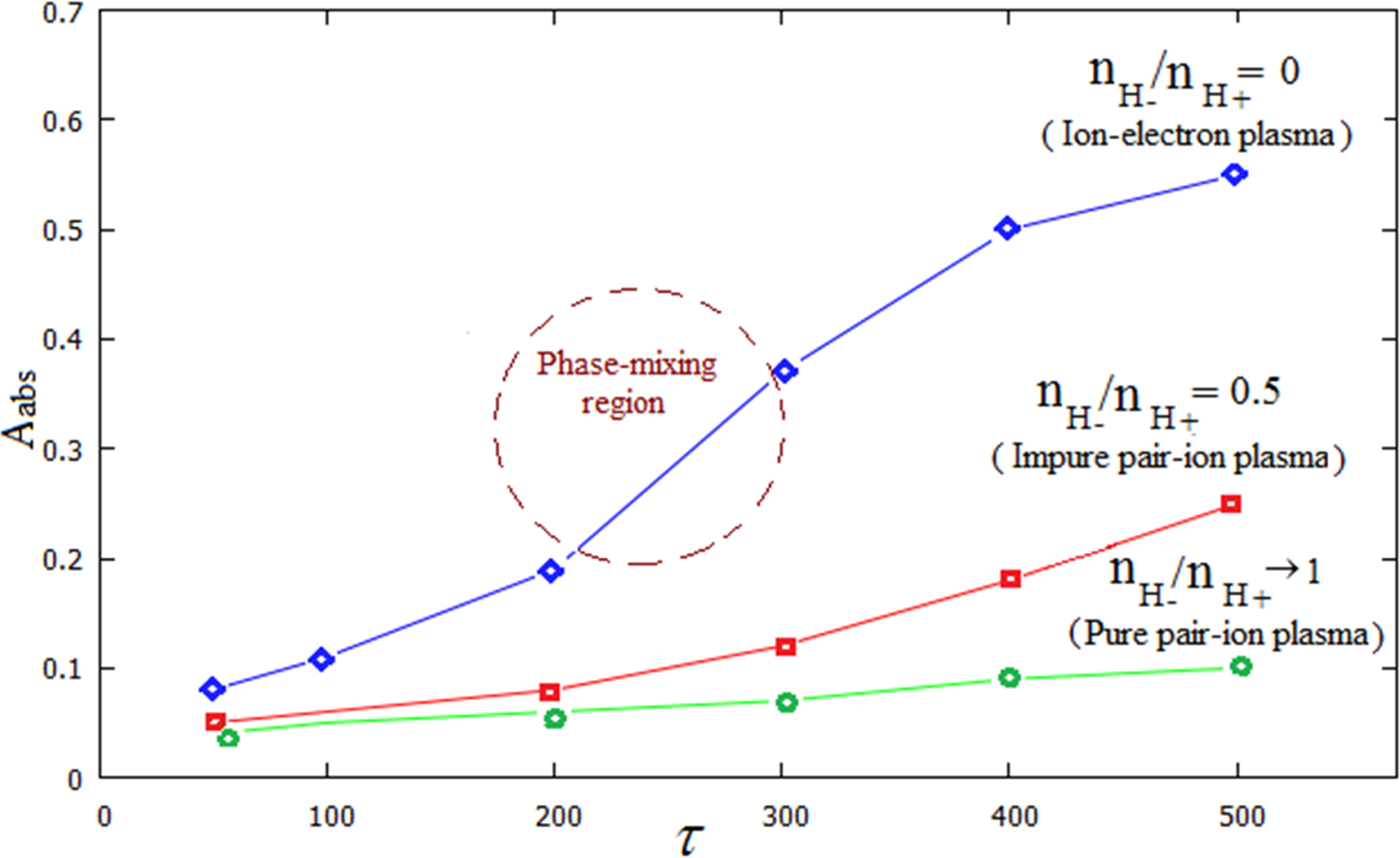
Fig. 4. Variation of the absorption rate of laser pulse (a = 2) versus time for interaction with nearly pure pair-ion plasma (green curve), impure pair-ion plasma (red curve), and hydrogen ion-electron plasma (blue curve). In this figure, the normalized positive hydrogen number density is n H+ = 0.1.
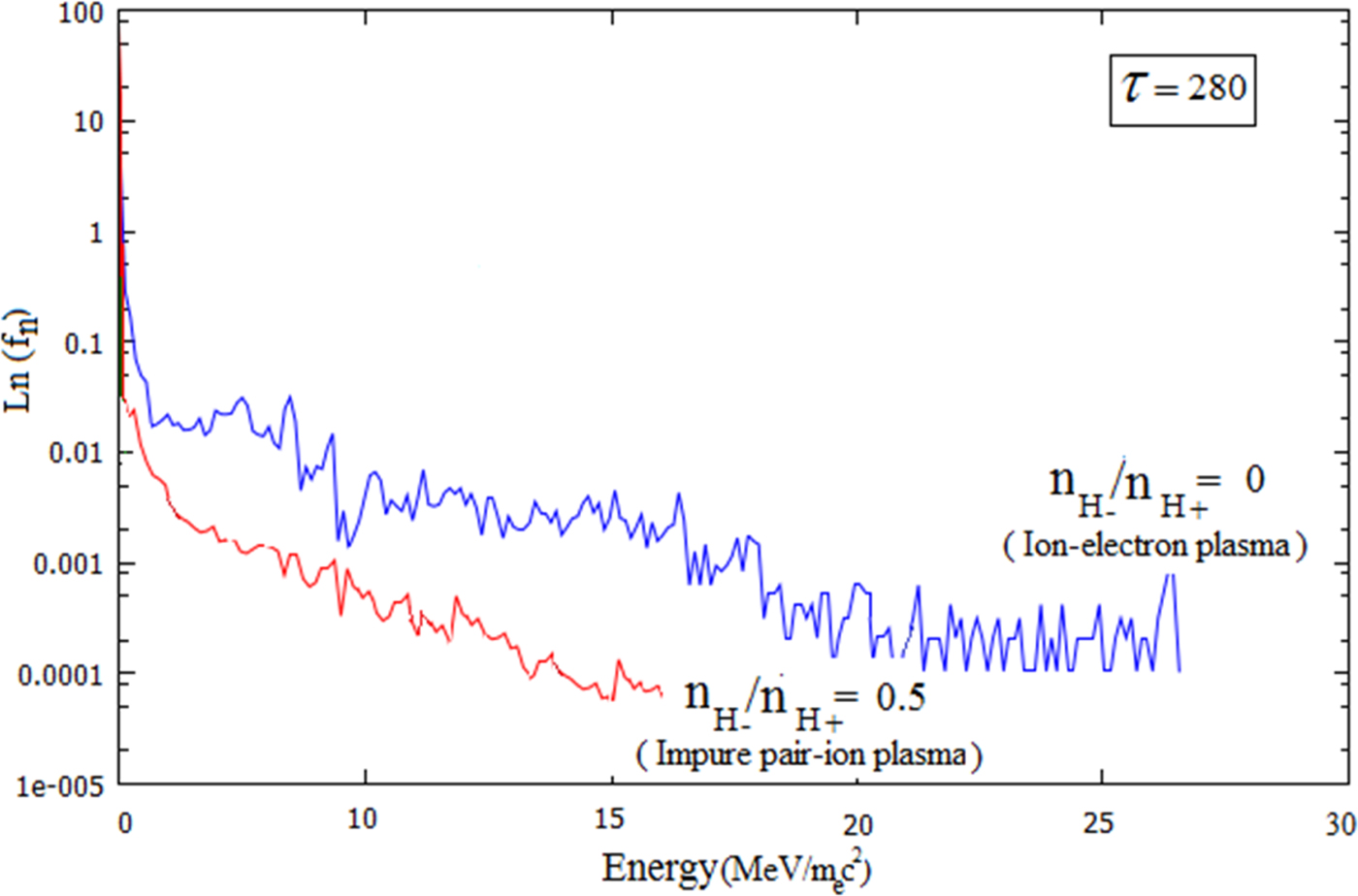
Fig. 5. Logarithmic spectrum for electrons in impure pair-ion plasma (red curve) and hydrogen ion-electron plasma (blue curve) with a = 2 and n H+ = 0.1. The energy axis has been normalized to m ec 2 ≅ 0.51 Mev.
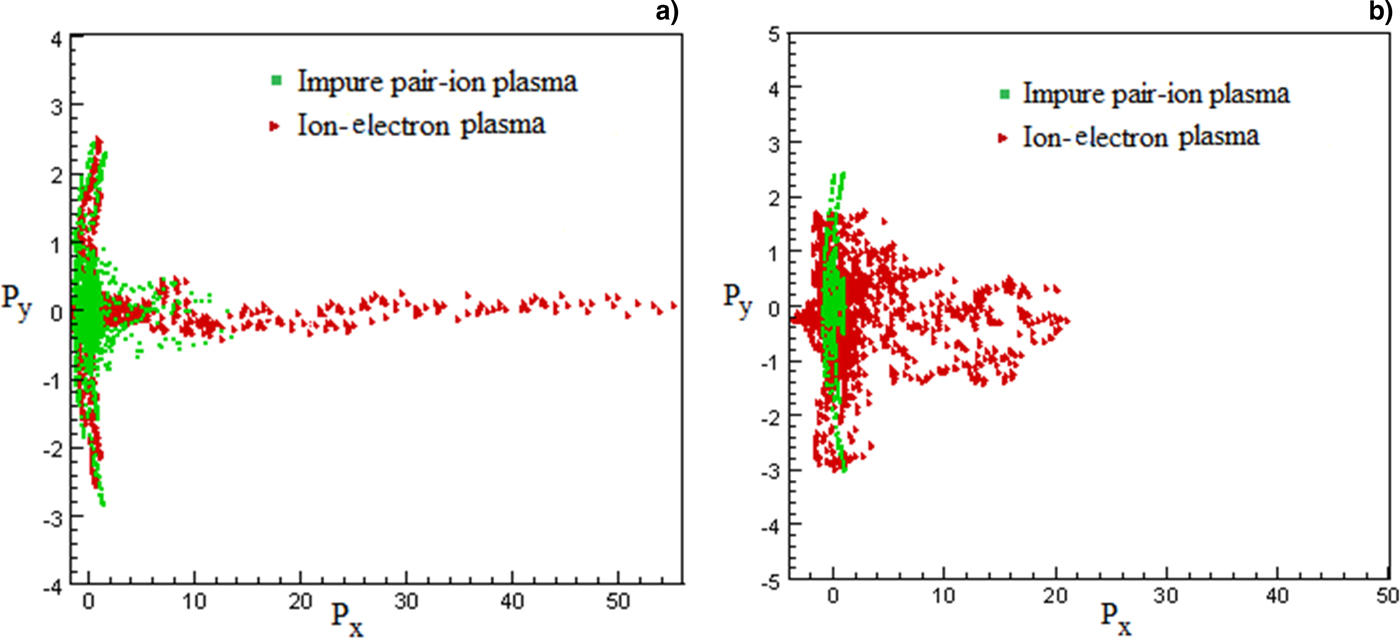
The snapshot of the electron distribution function at τ = 500 for hydrogen ion-electron plasma and impure pair-ion plasma is shown for plasma densities n H+ = 0.03 and n H+ = 0.1 in Figures 6a and 6b, respectively. As we expressed, the plasma particles can acquire further energy from the laser in a hydrogen ion-electron plasma than an impure pair-ion plasma. As an interesting result, investigation of the distribution functions shows that for low plasma densities (Fig. 6a) a large amount of laser energy is transferred to the electrons as directed kinetic energy (in the laser direction) to produce the electron beam in the MeV energy range. While for high densities (Fig. 6b) the laser energy is transferred to the particles as thermal energy due to the faster breaking of relativistic electron oscillations (wake wave breaking).
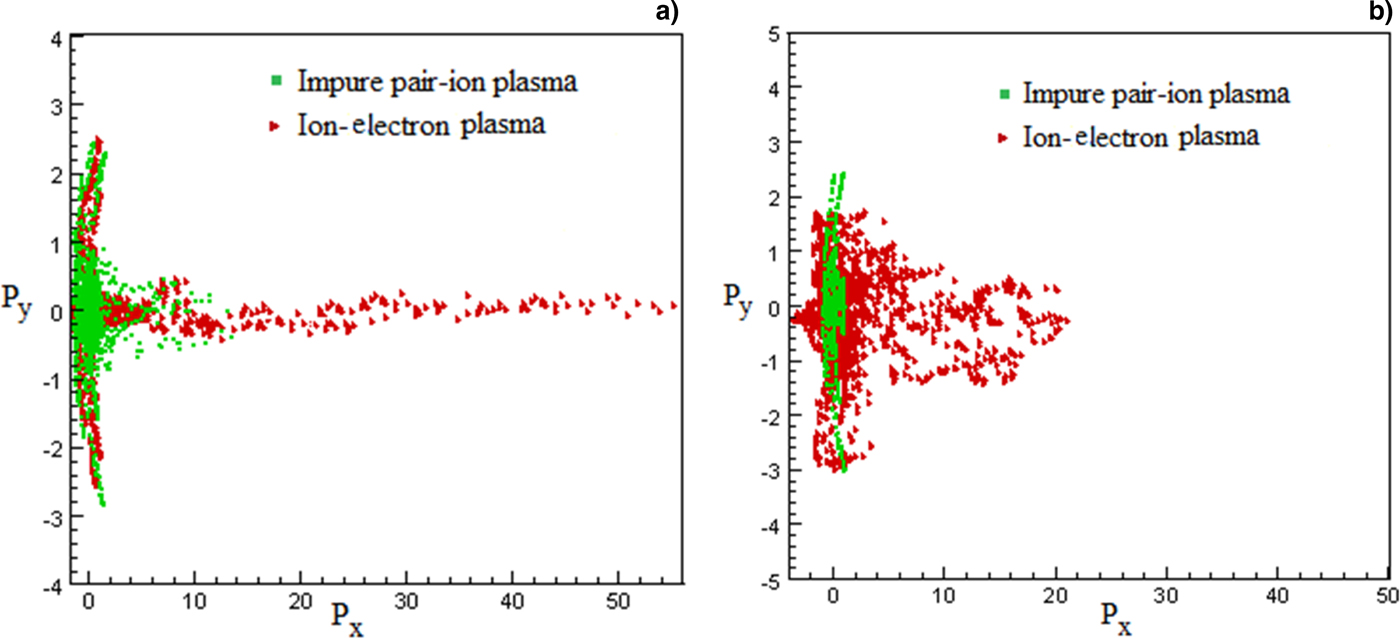
Fig. 6. Snapshots of the electron distribution function in impure pair-ion plasma (green dots) and in ion-electron plasma (red dots) for (a) n H+ = 0.03 and (b) n H+ = 0.1 at τ = 500.
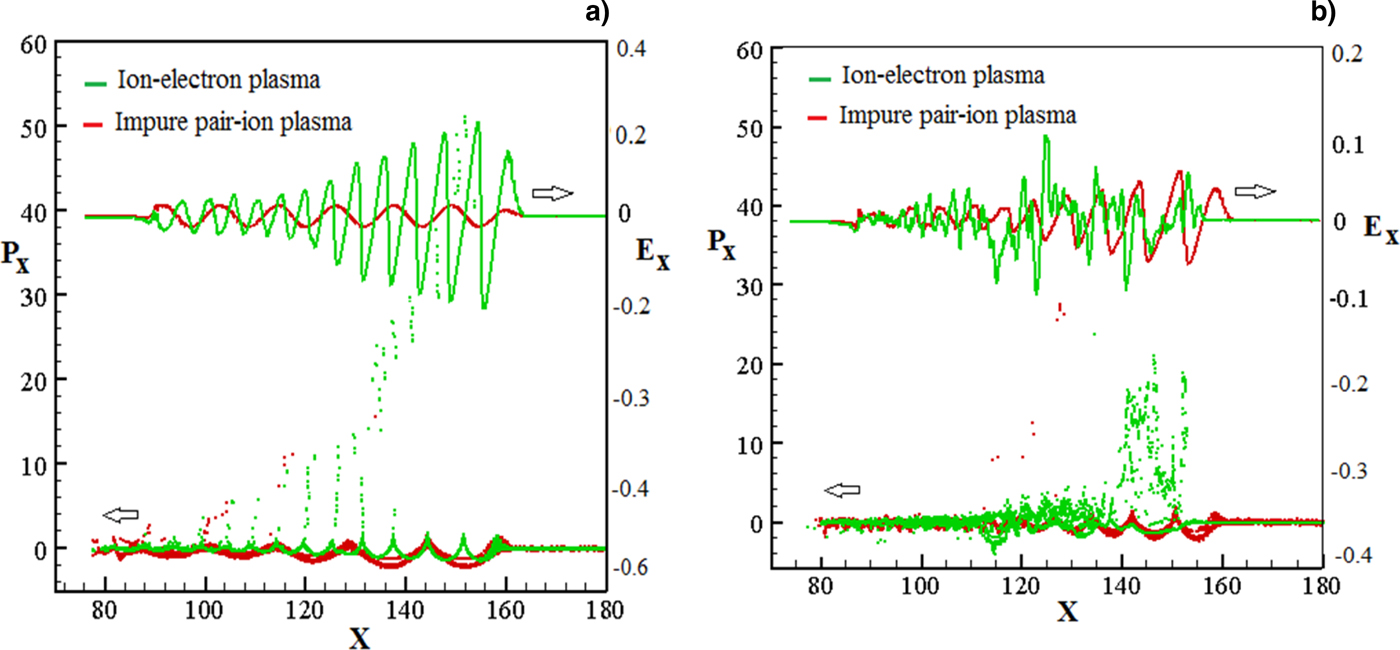
Finally, the longitudinal electric field profile combining with the phase-space of the particles in the x-direction (longitudinal phase-space) have been plotted for both ion-electron and impure pair-ion plasmas in low and high plasma densities in Figures 7a and 7b, respectively. For low density (see Fig. 7a) the acceleration of electrons in an ion-electron plasma by trapping process has been shown well, while this nonlinear process for the low-amplitude excited electric field in an impure pair ion plasma cannot a considerable role to accelerate the particles. However, in high density (see Fig. 7b) the excited electric field starts to break due to phase mixing or wave breaking and so, the transferred laser energy to the plasma particles is mostly as thermal energy. This is because the electrons do not move further in the trapping wave bubbles due to the breaking of these excited longitudinal waves.
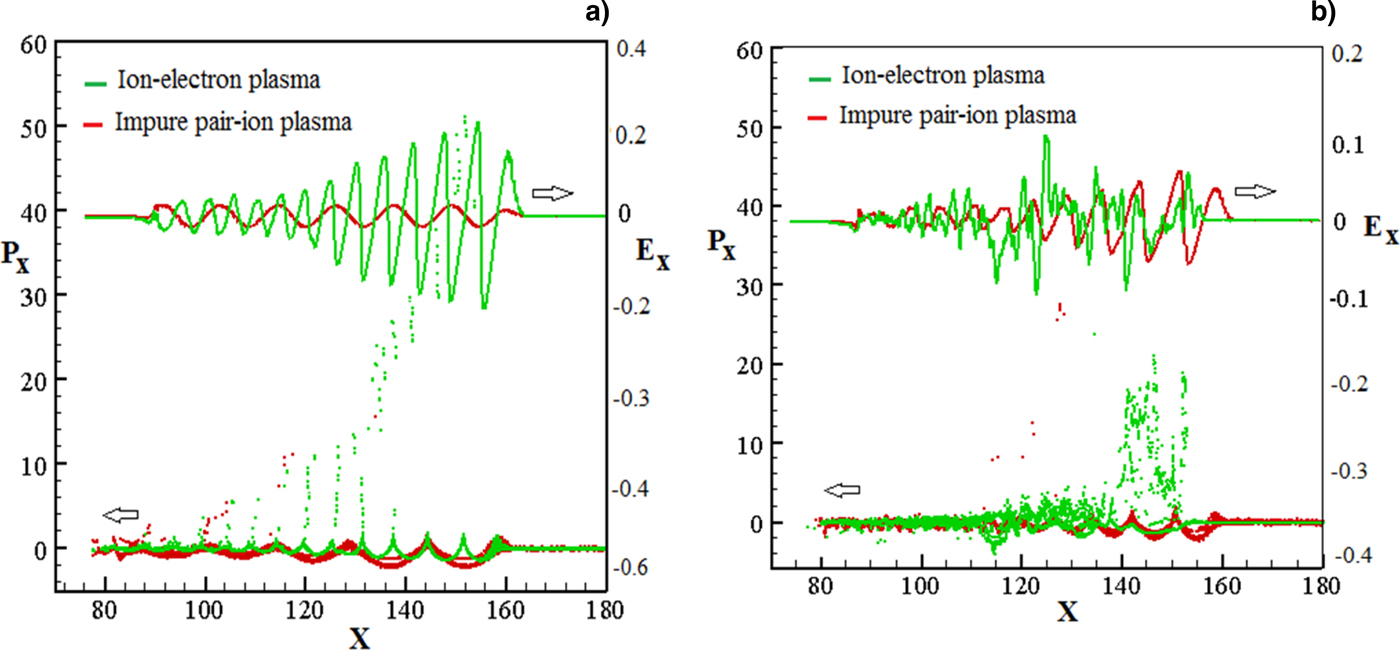
Fig. 7. Evolution of the normalized electric field and longitudinal phase-space for ion-electron (green line and dots) and impure pair-ion (red line and dots) plasmas for (a) low and (b) high plasma densities.
Conclusion
In summary, using the PIC simulation method, the laser energy absorption in both pure and impure hydrogen pair-ion plasmas containing electron impurities has been studied relying on the investigation of nonlinear phenomena contributing to the laser absorption such as the wave breaking, phase-mixing, and stimulated scattering. A careful scrutiny of the space-time evolution of the longitudinal space-phase and the fields associated with the laser and excited waves in the system shows that the inclusion of electron impurities into an initial pure pair-ion hydrogen plasma not only causes the occurrence of considerable stimulated scattering but also leads to the faster phase-mixing and wave breaking of the excited electrostatic modes in the system. Moreover, an investigation into the behavior of laser absorption rate in a finite-size pure and impure hydrogen pair-ion plasma demonstrates that the obtained nonlinear phenomena behaviors result in increasing the laser absorption rate in several orders of magnitude via inclusion of the electrons into a pure hydrogen pair-ion plasma target. Finally, as an interesting result, the distribution function of the involved species displays that the laser energy can be transferred to the included electrons to accelerate them in the laser direction in a specific range of the plasma density and an increase in this energy is directly proportional to the contribution of the electron impurities.