1. INTRODUCTION
At high laser intensities the interaction between a laser beam and plasma, gives rise to a variety of non-linear effects (Marklund & Shukla, Reference Marklund and Shukla2006; Ganeev et al., Reference Ganeev, Hutchison, Witting, Frank, Okell, Zaïr, Weber, Redkin, Lei, Roschuk, Maier, L'opez-Quintás, Martín, Castillejo, Tisch and Marangos2012; Weber & Riconda, Reference Weber and Riconda2015; Zhang et al., Reference Zhang, Ridgers and Thomas2015). These include harmonic generation (HG) (Upadhyay & Tripathi, Reference Upadhyay and Tripathi2005), wakefield acceleration (Ibbotson et al., Reference Ibbotson, Bourgeois, Rowlands-Rees, Caballero, Bajlekov, Walker, Kneip, Mangles, Nagel, Palmer, Delerue, Doucas, Urner, Chekhlov, Clarke, Divall, Ertel, Foster, Hawkes, Hooker, Parry, Rajeev, Streeter and Hooker2010), THz (terahertz) radiation generation (Kumar et al., Reference Kumar, Pandey, Cui and Nahata2011), and parametric instabilities (Klimo & Tikhonchuk, Reference Klimo and Tikhonchuk2013). HG has its applications in the diagnostic of non-linear medium, coherent multiphoton spectroscopy, and other phenomena (Döbele et al., Reference Döbele, Czarnetzki and Goehlich2000; Pirozhkov et al., Reference Pirozhkov, Bulanov, Esirkepov, Mori, Sagisaka and Daido2006; Li et al., Reference Li, Zhou, Ding, Du, Liu, Li, Wang, Sheng, Ma, Chen, Lu, Dong, Wang, Lou, Shi, Wei and Zhang2011; Liu et al., Reference Liu, Durand, Houard, Forestier, Couairon and Mysyrowicz2011). Much of the work on HG in laser-produced plasma has been reported by thin foils (Teubner et al., Reference Teubner, Wagner, Andiel, Pisani, Eidmann, Tsakiris, Schlegel, Förster and Witte2004), slab (Deb & Saha, Reference Deb and Saha2015), gas jet (Banerjee et al., Reference Banerjee, Valenzuela, Shah, Maksimchuk and Umstadter2003), and solid target (Dollar et al., Reference Dollar, Cummings, Chvykov, Willingale, Vargas, Yanovsky, Zulick, Maksimchuk, Thomas and Krushelnick2013). Some serious problems are encountered for HG from gaseous plasma, which encourages the researcher to use other targets. Increased value of laser intensity will increase harmonic intensity in gaseous plasma, cause rapid ionization of gaseous atoms, and decrease the harmonic emission. On the other hand, mismatch of the phase velocity of the laser beam and harmonic radiation affects the conversion efficiency. In a thin foil, harmonics have been mainly observed in reflection from the front side of massive solid targets. Efficiency of the yield can be increased by phase matching. It turns the process into a resonant one. Kaur and Sharma (Reference Kaur and Sharma2008) studied third HG in a laser-produced thin foil plasma with conversion efficiency obtained as 0.01%.
Currently, there is strong interest in intense short pulse laser interaction in plasma with ultrathin foils. One of the primary objectives is to achieve proton acceleration via TNSA (target normal sheath acceleration) or RPA (radiation pressure acceleration) mechanisms. In these studies, overdense plasma foils of thickness comparable with laser wavelength or much shorter wavelengths are employed (Tripathi et al., Reference Tripathi, Liu, Shao, Eliasson and Sagdeev2009). Adusumilli et al. (Reference Adusumilli, Goyal and Tripathi2011) have argued that when a laser beam of finite spot size (e.g., a Gaussian beam) impinges on an ultrathin foil, the radiation pressure it exerts on the foil is more on the axis and decreases with distance r. As a result, the foil acquires a curvature. The laser falling on the curved boundary is no longer normal to the boundary. Optical ray makes an angle to the surface normal. Under such a situation transmission coefficients for the s and p polarizations are different and transmitted wave does not maintain its circular polarization. They showed that s-polarized laser obliquely impinged on a foil can give rise to second-harmonic generation (SHG) in the direction of specular reflection. Their treatment is limited to semi-infinite plasma. SHG of a right circularly polarized Gaussian electromagnetic beam in an unbounded magnetized plasma has been investigated by Kaur et al. (Reference Kaur, Sharma and Salih2009). Self-focusing of the laser beam increases the yield of HG. For normalized amplitude of the short pulse eA 1/mωc = 0.3, HG efficiency exceeding 1%. Kaur et al. (Reference Kaur, Yadav and Sharma2010) have studied effect of self-focusing on resonant third HG for a Gaussian laser beam.
Singh and Gupta (Reference Singh and Gupta2015) investigated the effect of self-focusing of a q-Gaussian laser beam on SHG in a preformed parabolic plasma channel by using moment theory approach. Harmonics yield increases with the increase in intensity of laser beam, plasma density, and channel depth. Purohit et al. (Reference Purohit, Agrawal, Sharma and Parashar2013) have recently proposed SHG from a metallic thin film deposited over a glass half space. The laser is impinging obliquely on the film. The thin film has sufficiently high free carrier density, such that the harmonic is evanescent inside the film. They analyse the second harmonic in the reflected component and power conversion efficiency up to 10−5 has been obtained.
To overcome these limitations, overdense plasma came into play to generate higher order harmonics, which are free from phase-matching condition, results in higher harmonic order and intensity. Theoretical and experimentally studies have elucidated the two distinct processes, which are responsible for the HG from overdense plasma: coherent wakefield emission (CWE) and relativistic oscillating mirror (ROM) model. These both processes are very different although having a common origin, the Brunel process in which surface electrons, that is, Brunel electrons (Brunel, Reference Brunel1987) are first accelerated by laser field and then pushed back toward the plasma. In relativistic region, the ROM process dominates in which electrons are drawn out from the plasma surface. The critical surface from where the laser pulse reflects and oscillates with the velocity of light. During the period of laser-driving pulse, the phase of the reflected radiation redistributes due to the motion of the reflection point. This surface travels toward the laser due to which the pulse compresses causing the phase change leads to generation of high harmonics. A very fascinating experiment was performed by Streeter et al. (Reference Streeter, Foster, Cameron, Borghesi, Brenner, Carroll, Divall, Dover, Dromey, Gallegos, Green, Hawkes, Hooker, Kar, Mckeena, Nagel, Najmudin, Palmer, Prasad, Quinn, Rajeev, Robinson, Romagnani, Schreiber, Spindloe, Ter-Avetisyan, Tresca, Zepf and Neely2011) with 50 fs laser pulse of intensity between 1017 and 1021 W/cm2 incidents obliquely with p-polarization on aluminium target. They observed that for higher intensity >1020 W/cm2, the conversion efficiency of SHG was measured 22 (±8%). They compared the experimental results with ROM model and found that SHG efficiency depends on the intensity of the laser beam. Recently, Chen and Pukhov (Reference Chen and Pukhov2016) numerically simulated a scheme described by ROM model to produce bright high-order harmonics by controlling polarization.
In the sub-relativistic region, the CWE process dominates in which Brunel electrons come back to the plasma, some of them are temporally bunched and propagate across the density gradient of the plasma. As a consequence, the density gradient of the plasma accelerates and leads to generate electron plasma oscillations in their wake. These electrons are bunched temporally at the intervals of laser time period that excites the plasma frequencies resonantly which are multiples of the laser frequency. Consequently, harmonics are generated up to the plasma frequency related to maximum density of the target. Theoretical and experimental demonstration on high HG from overdense plasma with laser of moderate intensity is due to the CWE process given by Quere et al. (Reference Quere, Thaury, Monot, Dobosz and Martin2006).
Teubner et al. (Reference Teubner, Eidmann, Wagner, Andiel, Pisani, Tsakiris, Witte, Meyer-Ter-vehn, Schlegel and Förster2004) have experimentally demonstrated the generation of harmonics in laser-produced plasma from rear and front side of the thin overdense foil. They used foil made up of carbon and aluminium, thickness ranging from 50 to 460 nm. As p-polarized laser obliquely incident on thin foil at incidence angle of 45°, harmonics are generated. They observed that fundamental harmonic as well as harmonics up to 10th order are transmitted from the rear side besides those from the front side. By increasing foil thickness, harmonic emission efficiency of the reflected harmonics increases as compared with the transmitted harmonics. They also found that as the polarization of incident laser beam changes from p to s with normal incidence, no harmonics are generated. The experimental observations are reproduced by particle-in-cell (PIC) simulations using one-dimensional LPIC code. An experimental study of fundamental and second harmonics from the rear side of thin overdense foil from ultrashort laser pulse is demonstrated by Eidmann et al. (Reference Eidmann, Kawachi, Marcinkevičius, Bartlome, Tsakiris, Witte and Teubner2005). They examined the polarization properties, emission efficiencies and spectral shapes of the rear side harmonics. They found that p-polarized laser can generate significant rear side harmonics due to resonance absorption. The conversion efficiency enhances by increasing the laser intensity and reduces as the electron density increased in the foil. In these experiments, Brunel mechanism is responsible for the generation of harmonics from thin overdense foil. The rear side harmonic spectrum is broader than the incident laser light spectrum. The broadness of spectra increases with decreasing intensity and increasing foil thickness. This shows that duration of transmitted pulse is shorter than incident pulse. PIC simulation also supports the result.
In this paper, we study the generation of second harmonic of s-polarized laser from an overdense plasma slab, including multiple reflections of the incident as well as harmonic waves from both the front and rear surfaces. The second-harmonic ponderomotive force gives rise to electron oscillations at 2ω frequency, generating a second-harmonic current density. This current density is curl free in an uniform plasma and could produce only longitudinal field
$\; \vec E_{{\rm 2\omega}} $
. However, in the case of a bounded slab, it gives rise to appearance of space charges at the boundaries that lead to second-harmonic radiation on the reflection as well as transmission sides of the slab. Thus, sharp boundaries where electron density has large density gradient or a plasma with volume non-uniformity is essential for generating the harmonic.
In Section 2, we deduce an expression for non-linear current density due to s-polarized laser obliquely incident at an angle θ i on an overdense plasma slab. Second-harmonic field is deduced in Section 3 followed by results and discussion in Section 4.
2. NON-LINEAR CURRENT DENSITY
Consider a thin slab of overdense plasma of equilibrium electron density
$n_0^0 $
contained between z = 0 and z = d. A laser is obliquely incident from z < 0 side at angle of incidence θ
i
(cf. Fig. 1) with electric and magnetic fields as,
$$\vec E_i = \hat yA_0 e^{ - i({\rm \omega} t - ({\rm \omega} /c)\cos {\rm \theta} _i z - ({\rm \omega} /c)\sin {\rm \theta} _i x)}, $$
$$\vec B_i = \displaystyle{{A_0} \over c}( - \cos {\rm \theta} _i \hat x + \sin {\rm \theta} _i \hat z)e^{ - i({\rm \omega} t - ({\rm \omega} /c)\cos {\rm \theta} _i z - ({\rm \omega} /c)\sin {\rm \theta} _i x)}, $$
where
$\vec k = ({\rm \omega} /c)\sin {\rm \theta} _i \hat x + ({\rm \omega} /c)\cos {\rm \theta} _i \hat z$
, c is the speed of light in vacuum.
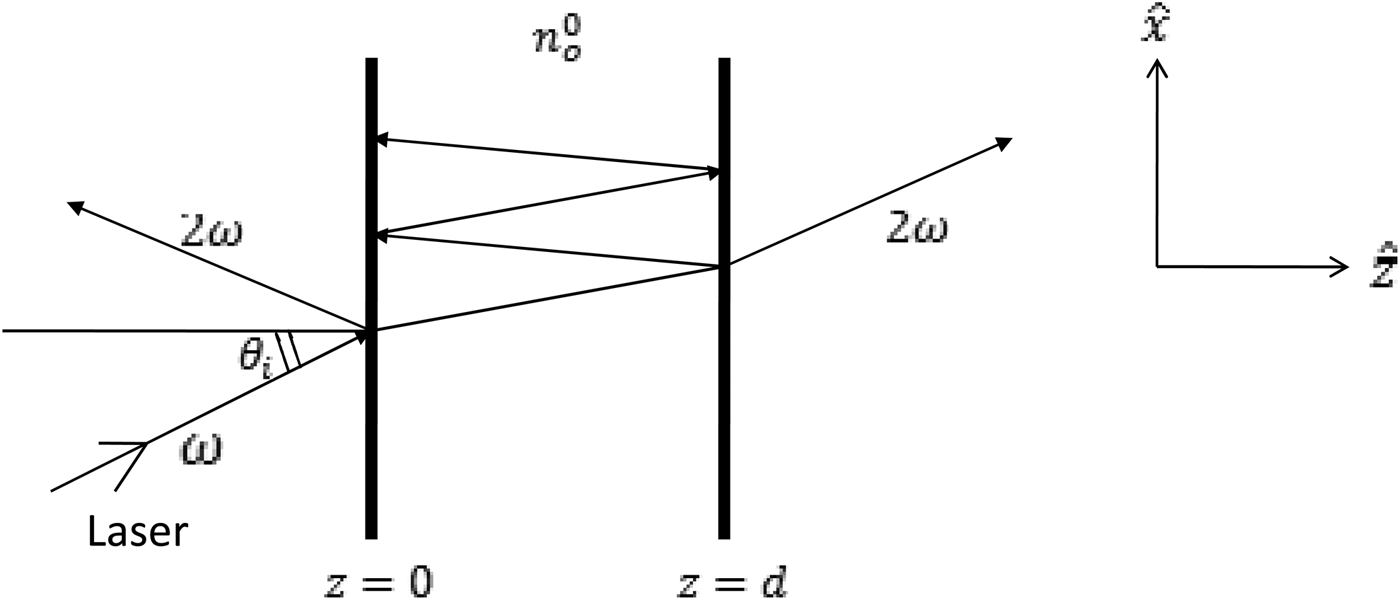
Fig. 1. Schematic presentation of SHG from a plasma slab.
Inside the plasma, the fields of the laser are,
$$\vec E_{{\rm II}} = \hat yA_0 \left[ {T_1 e^{ik_z z} + T_2 e^{ - ik_z z}} \right]e^{ - i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta} _i x)}, $$
$$\eqalign{\vec B_{{\rm II}} = & \displaystyle{{A_0} \over c}\left[ {(T_2 e^{ - ik_z z} - T_1 e^{ik_z z} )\displaystyle{{k_z c} \over {\rm \omega}} \hat x + (T_2 e^{ - ik_z z} + T_1 e^{ik_z z} )\sin {\rm \theta} _i \hat z} \right] \cr & \times e^{ - i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta} _i x)}.}$$
Following the conventional theory of linear reflection and transmission, we obtain
$$T_1 = \displaystyle{2 \over {D_1}} \left( {1 + \displaystyle{{ck_z} \over {{\rm \omega} \cos {\rm \theta} _i}}} \right),$$
$$T_2 = - \displaystyle{2 \over {D_1}} \left( {1 - \displaystyle{{ck_z} \over {{\rm \omega} \cos {\rm \theta} _i}}} \right)e^{2ik_z d}, $$
where
$$D_1 = \left[ {\left( {1 + \displaystyle{{ck_z} \over {{\rm \omega} \cos {\rm \theta} _i}}} \right)^2 - \left( {1 - \displaystyle{{ck_z} \over {{\rm \omega} \cos {\rm \theta} _i}}} \right)^2 e^{2ik_z d}} \right].$$
The laser imparts oscillatory velocity to electrons,
$\vec v_{\rm \omega} =(e\vec E_{{\rm II}} / mi{\rm \omega} )$
and exerts second-harmonic ponderomotive force on them,
$$\vec F_{\,p2{\rm \omega}} = - \displaystyle{m \over 2}\nabla (\vec v_{\rm \omega}. \vec v_{\rm \omega} ).$$
$$\eqalign{\vec{F}_{\,p2{\rm \omega}} & = \displaystyle{e^2 A_0^2 \over 2m {\rm \omega} ^2} \Bigg[\left(2i\displaystyle{{\rm \omega} \over c} \sin {\rm \theta}_i \right)(T_1^2 e^{2ik_z z} + T_2^2 e^{ - 2ik_z z} + 2T_1 T_2 )\hat{x} \cr & \quad + \,2ik_z (T_1^2 e^{2ik_z z} - T_2^2 e^{ - 2ik_z z} )\hat{z} \vphantom{{\rm \omega} \over c} \Bigg]e^{ - 2i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta}_i x)}.}$$
Using this in the equation of motion, we obtain the non-linear electron drift velocity at 2ω,
$$\eqalign{\vec{v}\,_{2{\rm \omega}}^{\rm NL} & = - \displaystyle{{e^2 A_0^2} \over {2m^2 {\rm \omega} ^3}} \left[\displaystyle{{\rm \omega} \over c} \sin {\rm \theta} _i (T_1^2 e^{2ik_z z} + T_2^2 e^{ - 2ik_z z} + 2T_1 T_2) \hat{x} \right. \cr & \left. \quad + \,k_z (T_1^2 e^{2ik_z z} - T_2^2 e^{ - 2ik_z z} )\hat{z}\right] e^{ - 2i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta}_i x)}.}$$
The equation of continuity yields the second-harmonic non-linear density perturbation,
$$\eqalign{n_{\rm 2\omega}^{\rm NL} & = - \displaystyle{{n_0^0 e^2 A_0^2} \over {2m^2 {\rm \omega}^4}} \displaystyle{{\rm \omega}^2 \over c^2} \left[{\rm \epsilon} (T_1^2 e^{2ik_z z} + T_2^2 e^{ - 2ik_z z} ) \right. \cr & \left. \quad + \,2T_1 T_2 {\rm sin}^2 {\rm \theta}_i \right] e^{ - 2i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta} _i x)},}$$
where
${\rm \epsilon} = 1 - {\rm \omega} _{\rm p}^2 /{\rm \omega} ^2 $
.
From the Poisson's equation, one obtains the second-harmonic field E
2,
$\nabla \cdot \vec E_2 = - ((e/{\rm \epsilon} _0 {\rm \epsilon} _2 )n_{\rm 2\omega}^{{\rm NL}} )$
, where
${\rm \epsilon} _2 = 1 - ({\rm \omega} _{\rm p}^2 /4{\rm \omega} ^2 )$
, ε
0 is the free space permittivity.
The non-linear current density at second harmonic is given by,
$${\vec J}_{2{\rm \omega}}^{\rm NL} = - n_0^0 e{\vec v}_{2{\rm \omega}}^{\rm NL},$$
$$\eqalign{{\vec J}_{2{\rm \omega}}^{\rm NL} = & \displaystyle{{n_0^0 e^3 A_0^2} \over {2m^2 {\rm \omega}^3}} \cr & \quad \times \left[\displaystyle{{\rm \omega} \over c}\sin {\rm \theta} _i (T_1^2 e^{2ik_z z} + T_2^2 e^{ - 2ik_z z} + 2T_1 T_2) {\hat x}\right. \cr & \quad \left. +\, k_z (T_1^2 e^{2ik_z z} - T_2^2 e^{ - 2ik_z z}) {\hat z} \right] e^{ - 2i({\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta} _i x)}.}$$
3. SECOND-HARMONIC FIELD
The wave equation governing the second-harmonic field inside the plasma is,
$$\nabla ^2 \vec E_2 + \displaystyle{{4{\rm \omega} ^2 - {\rm \omega} _{\rm p}^2} \over {c^2}} \vec E_2 = - i\displaystyle{{2{\rm \omega}} \over {c^2 {\rm \epsilon} _0}} \vec J_{{\rm 2\omega}} ^{{\rm NL}} + \nabla \left( { - \displaystyle{e \over {{\rm \epsilon} _0 {\rm \epsilon} _2}} n_{\rm 2\omega}^{{\rm NL}}} \right).$$
The second harmonic propagates in the x–z plane with t, x dependence as,
$$\vec E_2 = \vec F_2 (z)e^{ - 2i\left( {{\rm \omega} t - ({\rm \omega} /c)\sin {\rm \theta} _i x} \right)}. $$
Equation (11) in component for simplifies to
$$\eqalign{\displaystyle{{\partial ^2 F_2} \over {\partial z^2}} + K_{2z}^2 F_2 = &\, i\displaystyle{{{\rm \omega} _p^2} \over {c^2}} a_0 A_0 \sin {\rm \theta} _i \cr & \times \left[ (T_1 ^2 e^{2ik_z z} + T_2 ^2 e^{ - 2ik_z z} )\left( {\displaystyle{ \in \over { \in _2}} - 1} \right) \right. \cr & \left. +\, 2T_1 T_2 \left( {\displaystyle{{\sin {\rm \theta} _i ^2} \over { \in _2}} - 1} \right)\right]\hat x \cr&\!\! + i\displaystyle{{{\rm \omega} _p^2} \over {c^2}} a_0 A_0 \left( {\displaystyle{{k_z c} \over {\rm \omega}}} \right)[T_1 ^2 e^{2ik_z z} - T_2 ^2 e^{ - 2ik_z z} ]\left( {\displaystyle{ \in \over { \in _2}} - 1} \right)\hat z.} $$
The solution of x-component of wave equation is given by
$$\eqalign{F_{2X} & = A_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z z} + T_2^2 e^{ - 2ik_z z} ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 ) + A_{\rm 2}^{{\rm III}} e^{ik_{2z} z} \cr & \quad + A_{\rm 2}^{{\rm IV}} e^{ - ik_{2z} z}.}$$
The solution of the z-component of wave equation is
$$F_{2Z} = B_{\rm 2}^{\rm I} \left( {T_1^2 e^{2ik_z z} - T_2^2 e^{ - 2ik_z z}} \right) + B_{\rm 2}^{{\rm III}} e^{ik_{2z} z} + B_{\rm 2}^{{\rm IV}} e^{ - ik_{2z} z}. $$
The constants are obtained as
$$A_{\rm 2}^{\rm I} = \displaystyle{i \over 3}a_0 A_0 \sin {\rm \theta} _i \left( {\displaystyle{{\rm \epsilon} \over {{\rm \epsilon} _2}} - 1} \right),$$
$$A_{\rm 2}^{{\rm II}} = i\displaystyle{{{\rm \omega} _p^2} \over {c^2}} \displaystyle{{a_0 A_0 \sin {\rm \theta} _i} \over {k_{2z}^2}} \left( {\displaystyle{{{\rm sin}^{\rm 2} {\rm \theta} _i} \over {{\rm \epsilon} _2}} - 1} \right),$$
$$B_{\rm 2}^{\rm I} = ia_0 A_0 \left( {\displaystyle{{k_z c} \over {\rm \omega}}} \right)\left( {\displaystyle{{\rm \epsilon} \over {{\rm \epsilon} _2}} - 1} \right).$$
The solution of the wave equation on reflection side of the slab (z < 0) can be written as,
$$F_{2X} = A_2 e^{ - 2i({\rm \omega} /c)\cos {\rm \theta} _i z}, $$
$$F_{2Z} = \displaystyle{{\sin {\rm \theta} _i} \over {\cos {\rm \theta} _i}} A_2 e^{ - 2i({\rm \omega} /c)\cos {\rm \theta} _i z}. $$
While on the transmission side z > d,
$$F_{2X} = B_2 e^{2i({\rm \omega} /c)\cos {\rm \theta} _i z}, $$
$$F_{2Z} = - \displaystyle{{\sin {\rm \theta} _i} \over {\cos {\rm \theta} _i}} B_2 e^{2i({\rm \omega} /c)\cos {\rm \theta} _i z}. $$
For complimentary system
$\nabla \cdot E_2 = 0$
, we get
$$B_{\rm 2}^{{\rm III}} = - \displaystyle{{2{\rm \omega}} \over c}\displaystyle{{\sin {\rm \theta} _i} \over {k_{2z}}} A_{\rm 2}^{{\rm III}}, $$
$$B_{\rm 2}^{{\rm IV}} = \displaystyle{{2{\rm \omega}} \over c}\displaystyle{{\sin {\rm \theta} _i} \over {k_{2z}}} A_{\rm 2}^{{\rm IV}}. $$
Applying boundary conditions on tangential and axial component of electric field at interface z = 0 and z = d, we get,
$$\eqalign{&A_2 = A_{\rm 2}^{\rm I} (T_1^2 + T_2^2 ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 ) + A_{\rm 2}^{{\rm III}} + A_{\rm 2}^{{\rm IV}}, \cr & \!\!\tan {\rm \theta} _i A_2 = {\rm \epsilon} _2 B_{\rm 2}^{\rm I} (T_1^2 - T_2^2 ) + {\rm \epsilon} _2 B_{\rm 2}^{{\rm III}} + {\rm \epsilon} _2 B_{\rm 2}^{{\rm IV}}, \cr & A_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z d} + T_2^2 e^{ - 2ik_z d} ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 ) + A_{\rm 2}^{{\rm III}} e^{ik_{2z} d} + A_{\rm 2}^{{\rm IV}} e^{ - ik_{2z} d} \cr & \quad= B_2 e^{2i({\rm \omega} /c)\cos {\rm \theta} _i d}, \cr & {\rm \epsilon} _2 B_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z d} - T_2^2 e^{ - 2ik_z d} ) + {\rm \epsilon} _2 B_{\rm 2}^{{\rm III}} e^{ik_{2z} d} + {\rm \epsilon} _2 B_{\rm 2}^{{\rm IV}} e^{ - ik_{2z} d} \cr & \quad= - \tan {\rm \theta} _i B_2 e^{2i({\rm \omega} /c)\cos {\rm \theta} _i d}.}$$
Solving these equations, we obtain the second-harmonic amplitude in reflected and transmitted sides of the plasma slab,
$$\eqalign{A_2 & = A_{\rm 2}^{\rm I} (T_1^2 + T_2^2 ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 ) - \displaystyle{{\rm \alpha} \over {\rm \beta}} \cr & \quad + {\rm \lambda} \left[ { - 4\displaystyle{{{\rm \epsilon} _2} \over {\rm \beta}} \displaystyle{{\rm \omega} \over c}\displaystyle{{\sin {\rm \theta} _i} \over {k_{2z}}} {\rm \alpha \beta ^{\prime}}e^{ik_{2z} d} + 4{\rm \epsilon} _2 \displaystyle{{\rm \omega} \over c}\displaystyle{{\sin {\rm \theta} _i} \over {k_{2z}}} {\rm \delta}} \right],}$$
$$\eqalign{B_2 = \,& [A_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z d} + T_2^2 e^{ - 2ik_z d} ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 )]e^{ - 2i({\rm \omega} /c/)cos{\rm \theta} _i d} \cr &+ \left[ {{\rm \alpha \beta} {\rm ^{\prime}}{\rm \lambda}\over{\rm \beta}} \left\{ {tan{\rm \theta} _i (e^{2ik_{2z} d} - 1) - {\rm \epsilon} _2 \displaystyle{{2{\rm \omega}} \over c}\displaystyle{{\sin \theta _i} \over {k_{2z}}} (e^{2ik_{_2z} d} + 1)} \right\} \right] \cr &- {\rm \lambda \delta} \left\{\vphantom{\left( {{\rm \epsilon} _2 \displaystyle{{2{\rm \omega}} \over c}\displaystyle{{\sin {\rm \theta} _i (e^{ik_{2z} d} + e^{ - ik_2z d} )} \over {k_{2z}}}} \right)} tan{\rm \theta} _i (e^{ik_{2z} d} - e^{ - ik_{2z} d} ) \right. \cr & \left. - \left( {{\rm \epsilon} _2 \displaystyle{{2{\rm \omega}} \over c}\displaystyle{{\sin {\rm \theta} _i (e^{ik_{2z} d} + e^{ - ik_2z d} )} \over {k_{2z}}}} \right) \right\}e^{ - 2i({\rm \omega} /c)\cos {\rm \theta} _i d} \cr &- \displaystyle{{\rm \alpha} \over {\rm \beta}} e^{ik_{2z} d - i(2{\rm \omega} /c)\cos {\rm \theta} _i d},}$$
where
$\; \; {\rm \alpha} = \tan {\rm \theta} _i (A_{\rm 2}^{\rm I} (T_1^2 + T_2^2 ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 )) - {\rm \epsilon} _2 B_{\rm 2}^{\rm I} (T_1^2 - T_2^2 )$
,
${\rm \beta} = \tan {\rm \theta} _i + {\rm \epsilon} _2 \displaystyle{{2{\rm \omega}} / c}\ \displaystyle{{\sin {\rm \theta} _i} / {k_{2z}}}$
,
${\rm \beta '} = \tan {\rm \theta} _i - {\rm \epsilon} _2 \ \displaystyle{{2{\rm \omega}} / c}\displaystyle{{\sin {\rm \theta} _i} / {k_{2z}}}$
,
${\rm \delta} = \tan {\rm \theta} _i \left[ {A_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z d} + T_2^2 e^{ - 2ik_z d} ) + A_{\rm 2}^{{\rm II}} (2T_1 T_2 )} \right]+ {\rm \epsilon} _2 B_{\rm 2}^{\rm I} (T_1^2 e^{2ik_z d} - T_2^2 e^{ - 2ik_z d} )$
,
$\; {\rm \lambda} = \displaystyle{1 \over {{\rm \beta} {\rm ^{\prime}}^{\rm 2} e^{ik_{2z} d} - {\rm \beta} ^2 e^{ - ik_{2z} d}}}. $
We have plotted normalized second-harmonic amplitude A 2/A 0 and B 2/B 0 with respect to angle of incidence θ i , slab thickness, and plasma density. Figure 2 represents variation of normalized second-harmonic amplitude with angle of incidence in overdense plasma. The other parameters are: a 0 = 0.3, ωd/c = 5, ωp/ω = 3. At θ i = 0, the second harmonic is zero because current is normal to the plasma boundary and give rise to only space charge oscillations. At θ i = π/2, the laser penetration is too little inside the plasma, hence the HG vanishes. The yield of HG increases with the angle of incidence. It reaches maximum at θ i ≈ 50° and then decreases. The reflected amplitude peak is six times more than the transmitted amplitude peak. Figure 3 represents the variation of second-harmonic amplitude from an underdense plasma slab for ωp/ω = 0.7 and other parameters are same as Figure 2. Reflection side overdense plasma gives stronger SHG. However, for the transmission side underdense plasma is strong. This is because the plasma is transparent for the wave propagation, although the second-harmonic amplitude at transmission side is observed more than twice of an order of magnitude. The main motivation is indeed overdense plasma, although underdense plasma is studied for the sake of comparison and completeness.
Fig. 2. Normalized second-harmonic amplitude versus angle of incident in overdense plasma. The parameters are a 0 = 0.3, ωd/c = 5, ωp/ω = 3.
Fig. 3. Normalized second-harmonic amplitude versus angle of incident in underdense plasma. The parameters are a 0 = 0.3, ωd/c = 5, ωp/ω = 0.7.
Figure 4 represents the variation of second-harmonic amplitude with the thickness of the slab for the overdense plasma. The other parameters are ωp/ω = 3, θ i = 50°, and a 0 = 0.3. As we increases the thickness of the slab, the second harmonic on the reflection side initially increases and then saturates, where as in the transmission side, it initially increases then decreases and as the thickness of the slab increases, it tends to zero. Figure 5 represents the variation of second-harmonic amplitude versus thickness of the plasma slab in underdense plasma. The other parameters are ωp/ω = 0.7, θ i = 50°, and a 0 = 0.3. Oscillating behavior is observed for SHG on the reflected side. This is primarily due to the superposition of forward and backward propagating fundamental (ω frequency) waves inside the slab. However, in transmission side the yield of SHG increases and tends to saturates, when we increase the thickness of the slab, this is because due to continuous wave propagation.
Fig. 4. Normalized second-harmonic amplitude versus thickness of plasma slab for overdense plasma. The parameters are a 0 = 0.3, ωp/ω = 3, θ i = 50°.
Fig. 5. Normalized second-harmonic amplitude versus thickness of plasma slab for underdense plasma. The parameters are a 0 = 0.3, ωp/ω = 0.7, θ i = 50°.
Figure 6 represents the variation of normalized second harmonics with normalized plasma density. The other parameters are ωd/c = 5, θ i = 50°, and a 0 = 0.3. As the plasma density increases, the yield of second harmonic increases in both the reflected and the transmission sides. At ωp/ω = 2, there is resonant enhancement in the yield as the space charge oscillations induced by the ponderomotive force are resonantly enhanced. The singularity is masked by collisions. Beyond the singularity, the second-harmonic yield increases on the reflected side. However, due to higher plasma density, the wave does propagate in the transmission side, hence the yield is smaller.
Fig. 6. Normalized second-harmonic amplitude versus plasma density. The parameters are a 0 = 0.3, ωd/c = 5 and θ i = 50°.
4. DISCUSSION
An intense laser obliquely incident on an overdense thin slab plasma produces very significant second harmonic on the reflection as well as transmission sides. The yield of HG increases with the angle of incidence. For the parameters a 0 = 0.3, ωd/c = 5, ωp/ω = 3, and at incident angle θ i = 0, the second harmonic is zero because it gives rise to only space charge oscillations. It reaches maximum at θ i ≈ 50° and then decreases, both in the reflection and transmission sides of the slab. The intensity of transmitted second harmonic is smaller than that of the reflected harmonic. Thickness of the slab also affects the yield of HG. In the overdense case, reflection amplitude saturates for higher thickness, whereas transmission amplitude vanishes for ωp/ω = 2, as the second-harmonic wave becomes evanescent and very little second harmonic reaches the rear side. Oscillating behavior is observed for underdense plasma slab. However, in transmission side the yield of SHG tends to saturates, because the wave can continue to propagate. The main motivation is indeed overdense plasma, although underdense plasma is studied for the sake of comparison and completeness. Plasma density with optimum angle of incidence also affects the yield of SHG. At ωp/ω = 2, there is resonant enhancement in the yield as the space charge oscillation induced by the ponderomotive force are resonantly enhanced.
ACKNOWLEDGMENTS
The author is grateful to UGC-sanctioned UGC-BSR Research Start-Up-Grant No. F. 20-23(12)/2012(BSR) for supporting financially for the numerical computations. They are grateful to Professor V. K. Tripathi for simulating and useful discussion.
