Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T09:24:07.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Laser second harmonic generation in a rippled density plasma in the presence of azimuthal magnetic field

Published online by Cambridge University Press:  08 December 2009

U. Verma  and
A.K. Sharma
U. Verma*
Affiliation:
Center for Energy Studies, Indian Institute of TechnologyDelhi, New Delhi, India
A.K. Sharma
Affiliation:
Center for Energy Studies, Indian Institute of TechnologyDelhi, New Delhi, India
*
Address correspondence and reprint requests to: U. Verma, Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi-110016, India. E-mail: updeshv@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

The strong azimuthal magnetic fields, observed in many laser plasma experiments, are shown to be a potential source of second harmonic generation. The laser imparts oscillatory velocity to electrons and exerts a longitudinal pondromotive force on them. This force in conjunction with the azimuthal magnetic field and density ripple produces a second harmonic current with significant transverse component. The latter produces resonant second harmonic radiation.

Keywords

Azimuthal magnetic fieldLaserRipple densitySecond harmonic generation
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 4 , December 2009 , pp. 719 - 724
Copyright
Copyright © Cambridge University Press 2009

1. INTRODUCTION

Harmonic generation continues to be a fascinating field of research due to its various applications. Second harmonic generation (SHG) (Gupta et al., Reference Gupta, Sharma and Mahmoud2007; Sharma & Sharma, Reference Sharma and Sharma2009; Abdelli et al., Reference Abdelli, Khalfaoui and Ghohrini1992; Liu & Tripathi, Reference Liu and Tripathi1996; Giulietti, et al., Reference Giulietti, Banfi, Deha, Giulietti, Lucchesi, Nocera and Ze Zun1988; Upadhyay & Tripathi, Reference Upadhyay and Tripahi2005; Hafeez et al., Reference Hafeez, Shaikh and Baig2008; Ozaki et al., Reference Ozaki, Bom, Ganeev, Kieffer, Suzuki and Kuroda2007, Reference Ozaki, Bom and Ganeev2008; Liu et al., Reference Liu, Umstadter, Esarey and Ting1993; Huillier & Balcou, Reference Huillier and Balcou1993) has become one of the most investigated and discussed nonlinear optical process since 1961, when Franken et al. (Reference Franken, Hill, Peters and Weinreich1961) experimentally discovered SHG. The primary reason to investigate SHG has consistently been the achievement of efficient frequency doubling, the emphasis has been on phase-matched interaction between the fundamental and second harmonic beam. Phase matching is a condition that essentially requires conversion of linear momentum that also facilitates energy flow from the pump to the second harmonic signal. Experiments on electron and ion acceleration in a laser pulse field using sources of super intense radiation require high time contrast of femtosecond pulses. An efficient way to enhance the contrast is a nonlinear optical process of SHG. Second harmonic generation signals have well-defined polarizations, and thus SHG polarization anisotropy can be used to determine the orientation of proteins in tissues. It can be used in studying buried interfaces, as most surface science techniques cannot access such structures. SHG can provide information of the electric field at an interface. It allows the penetration of the laser power into the overdense region and provides a valuable diagnostics (Merdji et al., Reference Merdji, Guizard, Martin, Petite, Que're', Carre', Hergott, De' roff, Salie'res, Gobert, Meynadier and Perdrix2000; Verma et al., 2009; Panwar et al., 2009; Prasad et al., 2009) of various plasma processes (Dromey et al., Reference Dromey, Bellei, Carroll, Clarke, Green, Kar, Kneip, Markey, Nagel, Willingale, McKenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2009; Hafeez et al., Reference Hafeez, Shaikh and Baig2008). It also provides information about linear mode conversion of the laser into a plasma wave near the critical layer. It has been observed that the uniform plasmas cannot produce even harmonics neither by a plane nor by a circularly polarized electromagnetic wave. In most laser interactions with homogeneous plasma, odd harmonics are generated (Mori et al., Reference Mori, Decker and Leemans1993; Zeng et al., Reference Zens, Shen, Yu and Xu1996). Even harmonics can be produced in the presence of density gradient at an angle to the direction of the wave propagation (Esaray et al., Reference Esarey, Ting, Sprangle, Umstadter and Liu1993; Malka et al., Reference Malka, Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Danson, Neely and Walsh1997).

The current investigations are dealing with the study of pulsed SHG under condition of phase and group velocity mismatch, and low conversion efficiencies and pump intensities, in negative index materials called artificially engineered meta-materials (Ramakrishna, Reference Ramakrishna2005; Wang et al., Reference Wang, Luo, Peng, Huangfu, Jiang, Wang, Chen and Ran2009). Ultraviolet and X-ray SHG (Chen et al., Reference Chen, Zitter and Tao1995) in semiconductors have been reported, which shows that the subject is of interest for the purpose of realizing coherent sources. Centini et al. (Reference Centini, Roppo, Fazio, Pettazzi, Sibilia, Haus, Foreman, Akozbek, Bloemer and Scalora2008) shown theoretically and experimentally the inhibition of linear absorption for phase and group velocity mismatch second and third harmonic generation in strongly absorbing materials, GaAs, in particular, at frequency above the absorption edge. Schifano et al. (Reference Schifano, Baton, Biancalana, Giuletti, Giuletti, Labaune and Renard1994) experimentally investigated the properties of the second harmonic emission and tested the effectiveness of this emission as a diagnostics for plasma inhomogenities induced by filamentation. Mironov et al. (Reference Mironov, Lozhkarev, Ginzburg and Khazanov2009) recently observed the effect of instantaneous cubic nonlinearity on SHG of femtosecond laser pulses. They have also analyzed the possibility of improving generation efficiency and shortening pulse duration. He observed 60% energy conversion efficiency and showed that the additional correction of spectral phase at the SH significantly reduces pulse duration. Shen (Reference Shen1989) has shown that SHG is a versatile tool for studies of many kinds of surfaces and interfaces. Ultrashort laser pulses can be used to monitor surface dynamics and reaction with sub-picoseconds time resolution. Krushelnik et al. (Reference Krushelnick, Ting, Burris, Fisher, Manka and Esarey1995) observed second harmonic shifted by the plasma frequency giving information about the stimulated Raman process. Liu et al. (Reference Liu, Umstadter, Esarey and Ting1993) have observed harmonic generation using a 1 ps, 1 µm, variable intensity laser in hydrogen gas jet plasma produced by tunnel ionization. Parashar & Sharma (Reference Parashar and Sharma1998) have studied SHG by an obliquely incident laser on a vacuum-plasma interface and rippled metal surface. Dahiya et al. (Reference Dahiya, Sajal and Sharma2007) presented particle-in-cell (PIC) simulations of phase matched second and third harmonic in ripple density plasmas. Yadav et al. (2008) have investigated stimulated Compton scattering (SCS) and stimulated Brillion scattering (SBS) of second harmonic signals. Salih et al. (2003) have studied SHG in self-created magnetized plasmas. The harmonic amplitude shows resonant enhancement as ωc tends to ω. Kaur and Sharma (Reference Kaur and Sharma2009) and Kura et al. (Reference Kaur, Sharma and Salih2009) have shown in a collisional magnetoplasma the self-defocusing of the laser causes reduction in the efficiency of second harmonic generation. Recently Verma and Sharma (Reference Verma and Sharma2009) developed a paraxial theory of third harmonic generation by a finite spot size laser in a tunnel ionizing gas.

In this paper, we study the generation of second harmonic in the presence of magnetic field. Physical mechanism of generation of second harmonic is as follows: laser propagating through the plasma imparts oscillatory velocity on electrons and exerts a pondromotive force on them. This pondromotive force produces nonlinear oscillatory velocity at 2ω and then produces nonlinear current at 2ω frequency, hence second harmonic current is produced. In Section 2, we have calculated the linear and nonlinear current densities, and in Section 3 amplitude of second harmonic generation is calculated. Finally, in Section 4, we discuss the results.

2. CALCULATION OF LINEAR AND NONLINEAR CURRENT DENSITIES

Consider a laser produced plasma with rippled density n 0 = n 00 + n q, n q = n 0qe iqz, and sheared magnetic field,

(1)
\vec B_s=- \hat y\, B_0 {x \over {x_0 }}.

The magnetic field resembles azimuthal magnetic field in the slab model. A laser propagates through the plasma with electric field

(2)
\vec E_L=\hat x\, A_0 e^{ - x^2 /x_0^2 } e^{ - i\lpar \omega t - kz\rpar } .

It imparts oscillatory velocity to electrons,

\vec v_\omega={{e\vec E_L } \over {mi\omega }}\comma \;

where -e is the electronic charge, m is the mass of electron, and ω is the frequency of the laser, and we have assumed ω≫eB 0/m. The laser also exerts a second harmonic ponderomotive force on electrons

\vec F_{P\comma 2\omega }=e\nabla \phi_P\comma \;

where

(3)
\phi_{P\comma 2\omega }={{eE_L^2 } \over {2\, m\omega ^2 }}.

The electron response to $\vec F_{P\comma 2\omega }$ is governed by

m{{\partial \vec v^{NL}_{2\omega } } \over {\partial t}}=- \vec F_{P\comma 2\omega } - e\vec v^{NL}_{2\omega } \times \vec B_s.

Replacing ∇ by ik and ${\partial / {\partial t}}$ by −iω, we get

(4)
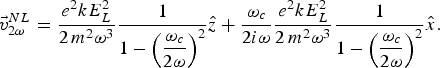
\vec v_{2\omega }^{NL}={{e^2 kE_L^2 } \over {2\, m^2 \omega ^3 }}{1 \over {1 - \left(\displaystyle {{{\omega_c } \over {2\omega }}} \right)^2 }}\hat z+{{\omega_c } \over {2i\omega }}{{e^2 kE_L^2 } \over {2\, m^2 \omega ^3 }}{1 \over {1 - \left(\displaystyle{{{\omega_c } \over {2\omega }}} \right)^2 }}\hat x.

The nonlinear second harmonic current density at (2ω, 2k+q) can be written as

(5)
\vec J_{2\omega }^{NL}=- {1 \over 2}n_q e\vec v_{2\omega }^{NL} .

One may note that the transverse component of second harmonic current density, J 2ω  xNL, scales as ωc, i.e., it is proportional to x, hence is zero on laser axis.

The linear response of electrons to the self-consistent second harmonic field $\vec E_{2\omega }$ is governed by

(6)
{{d\vec v_{2\omega }^L } \over {dt}}+\vec v_{2\omega }^L \times \vec \omega_c=- {e \over m}\vec E_{2\omega }.

Taking

(7)
\vec E_{2\omega }=\vec A_{2\omega } \, e^{ - i\lpar 2\omega t - k_2 z\rpar }\comma \; \, \vec \omega_c=- \hat y\, \omega_{c0} {x \over {x_0 }}\comma \;

one obtains

(8)
\eqalign{ v^L_{2x}&={{eE_{2\omega \, x} } \over {2im\omega }}+{{eE_{2\omega \, z} } \over {2im\omega }}{{\omega_c } \over {2i\omega }}\comma \; \, v^L_{2y}={{eE_{2\omega \,y} } \over {2im\omega }}\comma \; \cr&\quad v^L_{2z}={{eE_{2\omega \,z} } \over {2im\omega }} - {{eE_{2\omega \,x} } \over {2im\omega }}{{\omega_c } \over {2i\omega }}\comma \; }

where we have assumed $\left({{{\omega_c } / {2\omega }}} \right)^2 \; \ll \!1.$ The linear current density at 2ω can be written as

(9)
\vec J^L_{2\omega }=- n_0 e\vec v_{2\omega }^L=\, \underline{\underline {\sigma_2 }}.\vec E_{2\omega }\comma \;
\eqalign{ \sigma_{2zz}&=\sigma_{2yy}=\sigma_{2xx}=- {{n_0 e^2 } \over {2im\omega }}\comma \; \cr&\quad \sigma_{2xz}=- \sigma_{2zx}=- {{n_0 e^2 } \over {2im\omega }}{{\omega_c } \over {2i\omega }}\comma \; \cr&\quad \sigma_{2zy}=\sigma_{2xxy}=\sigma_{2yz}=0.}

3. SECOND HARMONIC GENERATION

The wave equation governing $\vec E_{2\omega }$ is

(10)
\nabla ^2 \vec E_{2\omega } - \nabla \lpar \nabla .\vec E_{2\omega } \rpar +{{4\omega ^2 } \over {c^2 }}\underline{\underline {\varepsilon_2 }} .\, \vec E_{2\omega }=- {{2i\omega } \over {c^2 \varepsilon_0 }}\vec J_{2\omega }^{NL} \comma \;

where

\eqalign{ \underline{\underline {\varepsilon_2 }}&=\underline{\underline I}+{i \over {2\omega \varepsilon_0 }}\underline{\underline {\sigma_2 }} \comma \; \, \varepsilon_{2xx}=\varepsilon_{2yy}=\varepsilon_{2zz}=1 - {{\omega_p^2 } \over {4\omega ^2 }}\comma \; \cr&\quad \varepsilon_{2xz}=- \varepsilon_{2zx}=\, i{{\omega_p^2 } \over {4\omega ^2 }}{{\omega_c } \over {2\omega }}\comma \; \cr&\quad \varepsilon_{2xy}=\varepsilon_{2yx}=\varepsilon_{2yz}=\varepsilon_{2zy}=0.}

Since $\vec E_{2\omega }$ has fast variation along $\hat z$ and slow in $\hat x$, i.e. ${\partial / {\partial x}}\ll {\partial / {\partial z}}$, we get from the z component of Eq. (10)

(11)
E_{2\omega \,z}=- {i \over {2\omega \varepsilon_0 }}{{\vec J_{2\omega }^{NL} } \over {\varepsilon_{2xx} }}+{{\varepsilon_{2xz} } \over {\varepsilon_{2xx} }}E_{2\omega \,x}+{{c^2 } \over {4\omega ^2 }}{1 \over {\varepsilon_{2xx} }}{{\partial ^2 } \over {\partial z\partial x}}E_{2\omega \,x} .

Using this value in the x component of Eq. (10) we get

(12)
\eqalign{ {{\partial ^2 } \over {\partial z^2 }}E_{2\omega \,x}&+{{\partial ^2 } \over {\partial x^2 }}E_{2\omega \,z}+{{4\omega ^2 } \over {c^2 }}\left({{{\varepsilon_{2xx}^2+\varepsilon_{2xz}^2 } \over {\varepsilon_{2xx}^2 }}} \right)E_{2\omega \,x}\cr&\quad =- {{2i\omega } \over {c^2 \varepsilon_0 }}J_{2\omega \,x}^{NL} - {{4\omega ^2 } \over {c^2 }}{{\varepsilon_{2xz} } \over {2i\omega \varepsilon_0 \varepsilon_{2xx} }}J_{2\omega \,z}^{NL}\cr&\qquad\; +{{\partial ^2 } \over {\partial z\partial x}}\left({{{J_{2\omega z}^{NL} } \over {2i\omega \varepsilon_0 \varepsilon_{2xx} }}} \right).}

Using the values of $\underline{\underline {\varepsilon_2 }}$ from above we may write

(13)
{{\varepsilon_{2xx}^2+\varepsilon_{2xz}^2 } \over {\varepsilon_{2xx}^2 }}\,= \,\varepsilon_{00} - \varepsilon_2 {{x^2 } \over {x_0^2 }}\comma \;

where $\omega_p^2=(n_0e^2/m\varepsilon_0)\comma\, \omega_{c0} = eB_0/m\comma\, \varepsilon_{00}=1 - ({{\omega_p^2 } / {4\omega ^2 }})$, and $\varepsilon_2=({{\omega_{c0}^2 } / {4\omega ^2 }}) ({\omega_p^2} / $$ {({4\omega ^2 - \omega_p^2}}))$. Then Eq. (12) can be written as

(14)
{{\partial ^2 } \over {\partial z^2 }}E_{2\omega \,x}+{{\partial ^2 } \over {\partial x^2 }}E_{2\omega \,z}+{{4\omega ^2 } \over {c^2 }}\left({\varepsilon_{00} - \varepsilon_2 {{x^2 } \over {x_0^2 }}} \right)E_{2\omega \,x}=R\comma \;

where

(15)
R=- {{2i\omega } \over {c^2 \varepsilon_0 }}J_{2\omega \,x}^{NL} - {{4\omega ^2 } \over {c^2 }}{{\varepsilon_{2xz} } \over {2i\omega \varepsilon_0 \varepsilon_{2xx} }}J_{2\omega \,z}^{NL}+{{\partial ^2 } \over {\partial z\partial x}}\left({{{J_{2\omega \,z}^{NL} } \over {2i\omega \varepsilon_0 \varepsilon_{2xx} }}} \right).

Writing

(16)
E_{2\omega \,x}=A_2 \lpar x\rpar e^{ - i\lpar 2\omega t - k_2 z\rpar } \hbox{ and } R=R_0 \lpar x\rpar e^{ - i\lpar 2\omega t - k_2 z\rpar }\comma \;

where k 2 = 2k + q, Eq. (14) can be written as

(17)
{2ik_2}{{\partial A_2}\over{\partial z}}+{{\partial ^2 } \over {\partial x^2 }}A_2+\left[{\left({{{4\omega ^2 } \over {c^2 }}\varepsilon_{00} - k_2^2 } \right)- {{4\omega ^2 } \over {c^2 }}\varepsilon_2 {{x^2 } \over {x_0^2 }}} \right]A_2=R_0 .

The phase matching condition for resonant second harmonic generation is

2\, k+q={{2\omega } \over c}\left({1 - \omega_p^2 /4\omega ^2 } \right)^{1/2}.

If right-hand-side of Eq. (17) is ignored, it resembles the Harmonic oscillator equation,

(18)
{{\partial ^2 A_2 } \over {\partial \xi ^2 }}+\left({\lambda_n - \xi ^2 } \right)A_2=0\comma \;

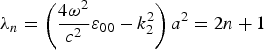with $\xi=x/a\comma \;$$\lambda_n=\left({{{4\omega ^2 } \over {c^2 }}\varepsilon_{00} - k_2^2 } \right)a^2=2n+1$ and $ a^2=({c/ {2\omega }})({{x_0 } /\!{\sqrt {\varepsilon_2 } }}).$ The above equation has bounded solutions. The first two Eigen modes with corresponding eigen values are

A_{21} \lpar \xi \rpar =e^{ - \xi ^2 /2}\comma \hbox{ for } n=0\, \comma \; \, \lambda_n=1\comma \;
(19)
A_{22} \lpar \xi \rpar =\xi \, e^{ - \xi ^2 /2}\comma \hbox{ for } n=1\, \comma \; \, \lambda_n=3.

Since R 0 is proportional to x, the coupling of only n = 1 mode of the second harmonic to the pump is relevant. In the presence of right-hand-side in Eq. (17), we presume that the mode structure of E 2ω remains the same but amplitude acquires a z-dependence. Thus, we write

(20)
A_2 \lpar x\comma \; z\rpar =F\lpar x\rpar G\lpar z\rpar \comma \;

where

(21)
F\lpar x\rpar =\lpar x/a\rpar \, e^{ - x^2 /2a^2 }\comma \;

substituting this in Eq. (17) multiplying the resulting equation by Fdx and integrating over x from −∞ to ∞, we get

{\partial \over {\partial z}}G\lpar z\rpar ={1 \over {2ik_2 \lpar \Gamma_{20} /a\rpar }}{{I_1 } \over {I_2 }}\comma \;

where

(22)
I_1=\vint\limits_{ - \infty }^\infty {R_0 \, x\, e^{ - x^2 /2a^2 } dx}\ \hbox{ and } I_2=\vint\limits_{ - \infty }^\infty {x^2 e^{ - x^2 /a^2 } dx} .

After solving it we get

(23)
\eqalign{\left\vert {G\lpar z\rpar } \right\vert& ={{A_0^2 a} \over {8ik_2 \sqrt 2 a^3 }}{{\omega_{\,pq}^2 \, ek\, z} \over {2\, m\omega ^3 \alpha ^{3/2} }}\cr&\quad \times\left[{{2 \over {x_0^2 }}{{k_2 } \over \omega }{1 \over {\left({1 - \omega_p^2 /4\omega ^2 } \right)}}+{{\omega_{c0} } \over {c^2 x_0 }}+{{\omega_p^2 } \over {4\omega ^2 }}{{\omega_{c0} } \over {c^2 x_0 }}} \right].}

The normalized second harmonic amplitude can be written as

(24)
\eqalign{& \left\vert {{{G\lpar z\rpar } \over {A_0 }}} \right\vert ={{a_0 } \over {16\sqrt 2 }}\left({{{n_{q0} } \over {n_0^0 }}} \right)\left({{{\omega_p^2 } \over {\omega ^2 }}} \right)\left({{k \over {k_2 }}} \right)\cr & \quad\times \left[{{\lpar 2\, k_2 /a^2 \alpha ^{3/2} \rpar \lpar \omega_p z/c\rpar \lpar \omega_p /\omega \rpar } \over {\lpar r_0 \omega_p /c\rpar ^2 \lpar 1 - \omega_p^2 /4\omega ^2 \rpar }}+{{\lpar \omega_{c0} /ca^2 \alpha ^{3/2} \rpar } \over {\lpar r_0 \omega_p /c\rpar }}\right.\cr&\quad \left.+{{\lpar \omega_{c0} /ca^2 \alpha ^{3/2} \rpar \lpar \omega_p^2 /4\omega ^2 \rpar \lpar \omega_p z/c\rpar } \over {\lpar r_0 \omega_p /c\rpar }} \right]}

where

{{2\, k_2 } \over {a^2 \alpha ^{3/2} }}={{8\lpar 1 - \omega_p^2 /4\omega ^2 \rpar ^{1/2} \sqrt {\varepsilon_2 } } \over {\matrix{\lpar r_0 \omega_p /c\rpar \lpar \omega_p /\omega \rpar ^2 \lsqb 2/\lpar r_0 \omega_p /c\rpar ^2\cr +\sqrt {\varepsilon_2 } /\lpar \omega_p /\omega \rpar \lpar r_0 \omega_p /c\rpar \rsqb ^{3/2}} }}\comma \;
{{\omega_{c0} } \over {ca^2 \alpha ^{3/2} }}={{2\sqrt {\varepsilon_2 } } \over {\matrix{\lpar r_0 \omega_p /c\rpar \lpar \omega_p /\omega \rpar \lpar \omega_p /\omega_{c0} \rpar \lsqb 2/\lpar r_0 \omega_p /c\rpar ^2 \cr + \sqrt {\varepsilon_2 } /\lpar \omega_p /\omega \rpar \lpar r_0 \omega_p /c\rpar \rsqb ^{3/2}}}}\comma \;

with $\alpha=({2 /{x_0^2 }})+({1 / {2a^2 })}$ and A 0 = amplitude of the laser.

We have solved Eq. (24) numerically for the following parameters: ωc0/ω = 0.2, 0.4, a 0 = 0.4, n q0/n 00 = 0.3, ωp2/ω2 = 0.05, 0.1 and ωpz/c = 1000.

In Figure 1, we have plotted the normalized second harmonic amplitude as a function ωpr 0/c for ωc0/ω = 0.2, and 0.4. At small laser spot size, the ratio of second harmonic amplitude to the amplitude of the fundamental wave is low as the electromagnetic modes are strongly localized. As the laser spot size grows, the no local effects. As the laser spot size grows, the nonlocal effects become important and magnetic field effects are there. As magnetic field increases i.e., ωc0/ω from 0.2 to 0.4 second harmonic generations become fast and its normalized amplitude increases from 0.09 to 0.185. This is due to the fact that as the laser goes into the plasma its spot size increases and magnetic field coupling becomes stronger and hence nonlinearity increases. Thus, more and more second harmonic generates. After some value of ωp r 0/c generation of second harmonic saturates. Since as the spot size becomes larger, non-local effects become un- important and hence the amplitude of the second harmonic saturates. In Figure 2, variation in normalized second harmonic amplitude is plotted with ωp r 0/c for different values of ωp2/ω2 = 0.05 and 0.1. Figure 2 shows that as the electron density increases more and more, the second harmonic generates likewise. By increasing the electron density, the nonlinearity increases. As SHG is a nonlinear phenomenon, it increases more and more. As ωp2/ω2 increases from = 0.05 to = 0.1 the amplitude of second harmonic increases from 0.135 to 0.195.

Fig. 1. Variation in normalized second harmonic amplitude with ωpr 0/c for ωc0/ω = 0.2 and 0.4. The other parameters are: a 0 = 0.4, n q0/n 00 = 0.3, ωp2/ω2 = 0.1 and ωpz/c = 1000.

Fig. 2. Variation in normalized second harmonic amplitude with ωpr 0/c for ωp2/ω2 = 0.05 and 0.1. The other parameters are: a 0 = 0.4, n q0/n 00 = 0.3, ωc0/ω = 0.4 and ωpz/c = 1000.

4. DISCUSSION

Second harmonic signals are very useful in reading DVD's as they can read a four times smaller area than the fundamental signal of the laser. We find that as magnetic field increases, generation of second harmonic becomes faster. This happens due to the strong coupling between magnetic field and laser field. Here ripple density provides phase matching between fundamental and second harmonic beam. Phase matching is a condition that essentially requires conversion of linear momentum that also facilitates energy flow from the pump to the second harmonic signal. Hence, more and more second harmonic generates. Electron density also plays important role since as electron density increases for particular value of magnetic field nonlinearity increases and hence second harmonic generation increases.

ACKNOWLEDGEMENT

The authors are grateful to Prof. V.K. Tripathi, IIT Delhi for fruitful discussions. The author is very thankful to the CSIR for financial support.

References

REFERENCES

Abdelli, S.Khalfaoui, T. & Ghohrini, D. (1992). Laser-plasma interaction properties through second harmonic generation. Laser Part. Beams 10, 629–637.CrossRefGoogle Scholar
Centini, M., Roppo, V., Fazio, E., Pettazzi, F., Sibilia, C., Haus, J.W., Foreman, J.V., Akozbek, N., Bloemer, M.J. & Scalora, M. (2008). Inhibition of linear absorption in opaque materials using phase-locked harmonic generation. Phys. Rev. Lett. 101, 113905.Google Scholar
Chen, T.J., Zitter, R.N. & Tao, R. (1995). Second-harmonic generation of nonlinear optical crystals in vacuum-ultraviolet and X-ray regions. Phys. Rev. A 51, 706–711.Google Scholar
Dahiya, D., Sajal, V. & Sharma, A.K. (2007). Phase-matched second and third-harmonic generation in plasmas with density ripple. Phys. Plasmas 14, 123104.Google Scholar
Dromey, B., Bellei, C., Carroll, D.C., Clarke, R.J., Green, J.S., Kar, S., Kneip, S., Markey, K., Nagel, S.R., Willingale, L., McKenna, P., Neely, D., Najmudin, Z., Krushelnick, K., Norreys, P.A. & Zepf, M. (2009). Third harmonic order imaging as a focal spot diagnostic for high intensity laser-solid interactions. Laser Part. Beams 27, 243–248.Google Scholar
Esarey, E., Ting, A., Sprangle, P., Umstadter, D. & Liu, X. (1993). Nonlinear analysis of relativistic harmonic generation by intense lasers in plasmas. IEEE Trans. Plasma Sci. 21, 95–104.CrossRefGoogle Scholar
Franken, P.A., Hill, A.E., Peters, C.W. & Weinreich, G. (1961). Generation of optical harmonics. Phys. Rev. Lett. 7, 118.Google Scholar
Giulietti, D., Banfi, G.P., Deha, I., Giulietti, A., Lucchesi, M., Nocera, L. & Ze Zun, Chen. (1988). Second harmonic generation in underdense plasma. Laser Part. Beams 6, 141–147.CrossRefGoogle Scholar
Gupta, M.K., Sharma, R.P. & Mahmoud, S.T. (2007). Generation of plasma wave and third harmonic generation at ultra relativistic laser power. Laser Part. Beams 25, 211–218.CrossRefGoogle Scholar
Hafeez, S., Shaikh, N.M. & Baig, M.A. (2008). Spectroscopic studies of Ca plasma generated by the fundamental, second, and third harmonics of a Nd:YAG laser. Laser Part. Beams 26, 41–50.CrossRefGoogle Scholar
Huillier, A.L. & Balcou, P. (1993). Higher order harmonic generation in rare gases with a 1-ps 1053–nm laser. Phys. Rev. Lett. 70, 1935.Google Scholar
Kaur, S. & Sharma, A.K. (2009). Self focusing of a laser pulse in plasma with periodic density ripple', Laser and Particle Beams, vol. 27, no. 2, pp. 193–199.CrossRefGoogle Scholar
Kaur, S., Sharma, A.K. &. Salih, H.A. (2009). Resonant second harmonic generation of a gaussian electromagnetic beam in a collisional magnetoplasma. Phys. Plasmas 16, 042509.Google Scholar
Krushelnick, K., Ting, A., Burris, H.R., Fisher, A., Manka, C. & Esarey, E. (1995). Second harmonic generation of stimulated raman scattered light in underdense plasmas. Phys. Rev. Lett. 75, 3681.Google Scholar
Liu, X., Umstadter, D., Esarey, E. & Ting, A. (1993). Harmonic generation by an intense laser pulse in neutral and ionized gases. IEEE Trans. Plasma Sci. 21, 90.Google Scholar
Liu, X., Umstadter, D., Esarey, E. & Ting, A. (1993). Harmonic generation by an intense laser pulse in neutral and ionized gases. IEEE Trans. Plasma Sci. 21, 90–93.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (1996). Second-harmonic generation of Raman scattered light in a plasma channel. Phys. Rev. E 54, 4098–4100.Google Scholar
Malka, V., Modena, A., Najmudin, Z., Dangor, A.E., Clayton, C.E., Marsh, K.A., Joshi, C., Danson, C., Neely, D. & Walsh, N. (1997). Second harmonic generation and its interaction with relativistic plasma wave driven by forward Raman instability in underdense plasmas. Phys. Plasmas 4, 1127–1131.Google Scholar
Merdji, H., Guizard, S., Martin, P., Petite, G., Que're', F., Carre', B., Hergott, J.F., De' roff, L., Salie'res, P., Gobert, O., Meynadier, P. & Perdrix, M. (2000). Ultrafast electron relaxation measurements on a-SiO2 using high-order harmonics generation. Laser Part. Beams 18, 489–494.Google Scholar
Mironov, S., Lozhkarev, V., Ginzburg, V. & Khazanov, E. (2009). High-efficiency second-harmonic generation of superintense ultrashort laser pulse. Appl. Opt. 48, 2051.CrossRefGoogle Scholar
Mori, W.B., Decker, C.D. & Leemans, W.P. (1993). Relativistic harmonic content of nonlinear electromagnetic waves in underdense plasmas. IEEE Trans. Plasma Sci. 21, 110.Google Scholar
Ozaki, T., Bom, L.B.E. & Ganeev, R.A. (2008). Extending the capabilities of ablation harmonics to shorter wavelengths and higher intensity. Laser Part. Beams 26, 235–240.Google Scholar
Ozaki, T., Bom, L.B.E., Ganeev, R., Kieffer, J.C., Suzuki, M. & Kuroda, H. (2007). Intense harmonic generation from silver ablation. Laser Part. Beams 25, 321–325.Google Scholar
Panwar, A. & Sharma, A.K. (2009). Self-phase modulation of a laser in self created plasma channel. Laser Part. Beams 27, 249–253CrossRefGoogle Scholar
Parashar, J. & Sharma, A.K. (1998). Second-harmonic generation by an obliquely incident laser on a vacuum-plasma interface. Europhys. Lett. 41, 389–394.Google Scholar
Prasad, R., Singh, R. & Tripathi, V.K. (2009). Effect of axial magnetic field and ion space charge on laser beat wave acceleration and surfatron acceleration of electrons. Laser part. Beams 27, 259–264.Google Scholar
Ramakrishna, S.A. (2005). Physics of negative refractive index materials. Rep. Prog. Phys. 68, 449–521.Google Scholar
Salih, H.A., Tripathi, V.K. & Pandey, B.K. (2003). Second-harmonic generation of a Gaussian laser beam in a self created magnetized plasma channel. IEEE Trans. Plasma Sci. 31, 324.Google Scholar
Schifano, E., Baton, S.D., Biancalana, V., Giuletti, A., Giuletti, D., Labaune, C. & Renard, N. (1994). Second harmonic emission from laser-preformed plasmas as a diagnostic for filamentation in various interaction condition. Laser Part. Beams 12, 435–144.Google Scholar
Sharma, R.P. & Sharma, P. (2009). Effect of laser beam filamentation on second harmonic spectrum in laser plasma interaction. Laser Part. Beams 27, 157–169.CrossRefGoogle Scholar
Shen, Y.R. (1989). Surface properties probed by second-harmonic and sum-frequency generation. Nat. 337, 519.Google Scholar
Upadhyay, A. & Tripahi, V.K. (2005). Second harmonic generation in a laser channel. J. Plasma Phys. 71, 359–366.Google Scholar
Verma, U. & Sharma, A.K. (2009). Effect of laser self defocusing on third harmonic generation in a tunnel ionizing gas. Phys. Plasmas 16, 013101.Google Scholar
Verma, U. & Sharma, A.K. (2009). Effect of self focusing on the prolongation laser produced plasma channel. Laser Part. Beams 27, 33–39.Google Scholar
Wang, Z., Luo, Y., Peng, L., Huangfu, J., Jiang, T., Wang, D., Chen, H. & Ran, L. (2009). Second-harmonic generation and spectrum modulation by an active nonlinear metamaterial. Appl. Phys. Lett. 94, 134102.Google Scholar
Yadav, S. & Tripathi, V.K. (2008). Second harmonic stimulated Compton scattering of laser in plasma. Phys. Sci. 77, 015501.CrossRefGoogle Scholar
Yadav, S., Kaur, S. & Tripathi, V.K. (2008). Stimulated brillouin scattering at the second harmonic of a laser in two-ion-species plasma. Phys. Sci. 78, 065501.Google Scholar
Zens, G., Shen, B., Yu, W. & Xu, Z. (1996). Relativistic harmonic generation excited in the ultrashort laser pulse regime. Phys. Plasmas 3, 4220.Google Scholar
Figure 0

Fig. 1. Variation in normalized second harmonic amplitude with ωpr0/c for ωc0/ω = 0.2 and 0.4. The other parameters are: a0 = 0.4, nq0/n00 = 0.3, ωp2/ω2 = 0.1 and ωpz/c = 1000.

Figure 1

Fig. 2. Variation in normalized second harmonic amplitude with ωpr0/c for ωp2/ω2 = 0.05 and 0.1. The other parameters are: a0 = 0.4, nq0/n00 = 0.3, ωc0/ω = 0.4 and ωpz/c = 1000.