1. INTRODUCTION
The intensive laser radiation interaction with a target was studied, due to wide technological applications (Bussoli, 2007; Bashir, 2007; Schade et al., 2006; Wieger et al., 2006; Trusso et al., 2005), and in order to obtain detailed knowledge about the physics of the involved interaction phenomena (Eliezer et al., 2005; Fisher et al., 2005; Hoffmann et al., 2005; Schaumann et al., 2005). Laser pulsed power have been extensively used in surfaces processing (Fernandez et al., 2005), and thin film deposition (Veiko et al., 2006), as well as to produce high temperature and high dense plasma for fusion devices, which were developed in the latter decades (See Anisimov et al., 1993; Gamaly et al., 1999, 2005; Singh & Narayan, 1990). The laser radiation absorbed in a certain target layer near the surface leads to ejection of target material in the form of vapor and droplets. For laser radiation power lower than some critical value, the ablation matter is heated and vaporized directly by the laser beam (Anisimov et al., 1971; Bogaerts et al., 2003). For sufficiently high power flux (>1 MW/cm2), the laser beam evaporates and ionizes the material, creating a plasma plume near the target surface. Since the species in the plasma interact with the target, then the phenomena should be taken into account, considering the mechanism of plasma generation (Lu & Hong, 1999).
The plasma interaction with a solid surface is a complicated phenomenon which includes absorption of the incident laser radiation, emission of electrons from the hot target, plasma heating, and electrical sheath formation at the target–plasma interface. The vaporization and plasma creation at the target surface, under large vapor pressure in the hot spot is the factor which is important in laser technology and laser diagnostics. A clear understanding of the laser ablation phenomena and common plasma processes are necessary for the control of laser processing.
A laser generated plasma expansion and plasma deposition at a substrate assuming high dense and high temperature, initially confined as small dimension plasma configuration, was theoretically studied by Singh and Narayan (1990). The surface ionization of evaporated atoms by Langmuir–Saha mechanism was assumed. The pulsed laser evaporation process was considered as an interaction of laser beam with bulk target, plasma formation, and isothermal initial expansion, which occur during the laser pulse duration, while the adiabatic expansion and deposition of thin film was studied when the laser pulse terminates. The Gaussian profile of the heavy particle density and vapor pressure distribution was given in the first two stages, while no vapor generation from the target was considered by adiabatic plasma expansion. The plasma expansion and deposition characteristics (velocity, thickness) were calculated as dependencies on plasma temperature, and surface temperature which were given as parameters. An increase of expanding plasma velocity with plasma temperature was calculated and indicated that the predicted increase of the plasma velocity with laser energy density agree with the measurements.
Gamaly et al. (1999) described the process of vaporization of a target material; the properties of the vapor, plasma flow, and film deposition on a substrate for high repetition rate laser evaporation was studied. For this purpose, the evaporation atom flux was previously described for a single pulse and for different conditions of absorbed laser radiation (<1010 W/cm2), solving the target one-dimensional (1D) heat conduction equation. In case of absorption at the vapor–solid interface, all parameters at the interface between solid and vapor are related to the absorbed laser intensity via conservation laws for mass, momentum, and energy. The vapor was considered as an ideal gas with an adiabatic exponent and sound velocity. It was indicated that the proposed theoretical method allowed one to define the optimal conditions for efficient evaporation of a target, with given thermodynamic properties.
An overview of different modeling approaches was reported by Bogaerts et al. (2003) for laser interaction with a matter operating in different regimes of wavelength (UV, Vis, IR), laser irradiance (104–1010 W/cm2), pulse length (fs, ps, ns). It was concluded that the entire process of laser ablation and the subsequent behavior of the ablated material cannot be described with one single model, and therefore, it should be described step by step taking into account target heating, melting and vaporization, plume expansion in a vacuum, and plasma shielding of the incoming laser light. Such a numerical model was developed by Bogaerts et al. (2003) and Chen and Bogaerts (2005) for Cu target. The target heat conduction equation was solved in a 1D approximation. The plasma formation was considered near the target surface, where the ions and electrons emission from the heated surface is described by the Langmuir–Saha equation and in the vapor volume by Cu atom ionization to Cu+ and Cu++ ions by the Saha–Eggert equations, assuming common temperature for the electrons, ions, and neutrals. This temperature was determined by the laser beam absorption in plasma which was accelerated during its expansion. The plasma expansion was calculated using an equilibrium condition for the pressure and vapor density, and thermal velocity for evaporated atoms.
Itina et al. (2002) proposed a three-dimensional (3D) combined model to describe the laser induced plasma plume expansion in a vacuum or into a background gas. The model takes into account the mass diffusion and energy exchange between the ablated and background species, as well as the collective motion of the ablated species, and the background-gas particles. Anisimov's (1968) results are used as a boundary condition, including the Mach number M = 1 at the Knudsen layer and one-atomic vapor (γ = 5/3). Only a singly charged ion was assumed. It was mentioned that the temperature of electrons deviates from that of ions and neutrals. However, no information about the data of electron temperature as a boundary condition and in the expanding plasma was presented.
Recently Gusarov and Aoki (2005) considered the thermal emission of electrons from Cu and Al targets, kinetics of ions and neutrals, and an electrostatic sheath that was formed at the surface. The potential drop in the electrostatic sheath was determined taking into account the electron fluxes from the target and plasma. The problem was solved for weakly ionized vapor and given plasma pressure at the external boundary of the Knudsen layer, as a parameter assuming temperature equilibrium for the plasma particles. A theoretical modeling of expanding plasma plume induced during welding of iron sheets with CO2 laser in a shielding gas (argon, helium) was developed by Moscicki et al. (2006). The set of equations consists of the equations of conservation of mass, energy, momentum, and the diffusion equation was solved for a given vapor velocity and temperature, as well as given gas dynamic parameters of the flow shielding gas. The main goal of this work was to study the interaction vapor–gas taking into account two plasmas-shielding gas plasma and metal plasma.
Thus, different approaches were considered previously assuming an equilibrium boundary condition for plasma expansion, thermal equilibrium in the plasma or weakly ionized vapor, neglecting collisions between charged particles, and local sound speed vapor flow in the Knudsen layer. The used Langmuir–Saha equation is not available to describe the surface ionization mechanism, when the potential of ionization of the atom is larger than the target work function. At the same time, the previous calculation indicated a relatively large particle temperature and a large degree of ionization of the vapor. Therefore, a space charge region with high potential drop and large electrical field at the surface, and as a result, large ion and electron emission currents at the target can be expected. In this case, there were the following important questions:
What is the plasma structure in the near target region by plasma target interaction?
How does the ion heat flux influence the target heat balance?
How does the energy of emitted electrons influence the plasma energy balance?
These problems were not considered previously. Our preliminary calculation with given plasma jet velocity as a parameter showed that the plasma generation depended on the energy exchange at the target-plasma interface (Beilis, 2006). In this work, an extensive physical model and a mathematical formulation to describe the laser generated plasma interaction with a target will be developed. The target ablation due to laser irradiation and the plasma energy flux (of ions and electrons), the space charge sheath, as well as the adjacent plasma heating by electron beam and plasma expansion into a vacuum will be considered. As the main point of the present work will be to study the physics of plasma interaction with a target, the laser power absorption in the expanding plasma will be taken in account by effective coefficients using published results described as a well known mechanism of such absorption.
2. MODEL AND SYSTEM OF EQUATION
The plasma generated near the target by laser (Anisimov et al., 1971; Gamaly et al., 1999; Bogaerts et al., 2003) and the plasma generated in the cathode region of a vacuum arc (Beilis, 1995) have similar characteristics. Both plasmas are very dense and appear in a minute region, known as laser spot and cathode spot, respectively. It is expected that the character of plasma interaction with matter in both cases are also similar. We develop here a model based on a previously presented kinetic model of the cathode spot by Beilis (1995, 2001, 2003) and modify it for the particular features of laser generated plasma. It will be taken into account that the net electrical current is zero in the laser spot, in contrast to the current carrying a vacuum arc cathode spot. It was assumed that the spot is circular with radius Rs, and located on a smooth surface. The near target vapor is a partially ionized gas that is separated from the surface by an electrical sheath across which there is a potential drop Ush, and in which charged particles are accelerated. There are two groups of electrons: (1) accelerated electrons emitted from the heated target and (2) slow plasma electrons. The energy of emitted electrons dissipates in the electron beam relaxation zone. Since the energy of accelerated electron beam exceeds the slow electron energy by an order of magnitude, then the electron beam relaxation zone is much larger than the ion or electron mean free path. Thus, inside the relatively large electron beam relaxation zone, a collision dominated plasma is formed which is heated by the accelerated electrons.
Near the heated surface, the ionized vapor is not in equilibrium, and a kinetic (Knudsen) layer of several ion mean free path lengths in which the particle function distribution approaches equilibrium is formed. This layer should be considered in the hydrodynamic treatment as a discontinuity region, where two heavy particle fluxes are produced. The first is a flux of atoms evaporated from the target (Langmuir flux) at a rate of evaporation W(T0), where T0 is the surface temperature. The second is a back-flow of atoms and ions, from the plasma toward the target surface. The difference of these fluxes determines the velocity of the mass flow and the net target evaporation rate G. The ratio of net evaporation rate to the total evaporated mass flux determines the target mass loss fraction

The origin of the coordinate system is defined at the target surface, and the x-direction coincides with the direction of the vapor flow. Four characteristic boundaries can be distinguished in the near-cathode region indicated by 1, 2, 3, and 4 (Fig. 1). Boundary 1 is at the target surface (x = 0), boundary 2 is at the external boundary of space charge sheath which is the ballistic zone, boundary 3 is at a distance of the Knudsen layer length from the cathode surface for heavy particles, and boundary 4 is located at a distance equal to the electron emission beam relaxation (in low energy plasma electrons) length from the target surface. The gas parameters, i.e., density, velocity, and temperature, at these boundaries are denoted as nαj, uαj, Tαj, where indices α − e, i, a, are the electrons, ions, atoms, respectively, and j = 1, 2, 3, 4 indicates the boundary number, and ne0 and n0 are the equilibrium electron and heavy particle densities determined by the target surface temperature T0 from equations for electron emission current density jem and saturated heavy particle flux from the target.

Schematic presentation of the layers and control boundaries in plasma near a target.
In order to determine the parameters at the above mentioned boundaries, the conservation equations of mass, momentum, and energy were integrated, taking into account the velocity of the ionized vapor uα and the particle velocity distribution function (VDF) at the control boundaries. Such an approach was proposed by Anisimov (1968) for laser evaporation of metals in form of neutral atoms. According to this model, the distribution function within the non-equilibrium layer can be approximated by the sum of two known terms before and after the discontinuity with coordinate-dependent coefficients. The model was extended by Beilis (1982, 1995) for electron emitted metals in form of charge particle evaporation and plasma flow in the Knudsen layer.
Let us consider the particle flow between the boundaries. The evaporated atoms have a half-Maxwellian VDF and this DF was served as boundary condition at the evaporated surface x = 0 with the surface temperature and a given density. In the region between boundaries 1 and 2, the plasma electrons are returned, while the ions and emitted electrons are accelerated with energy eUsh. At boundary 2, the ion velocity is determined by the condition at the sheath-plasma interface and then the ions (mass m) are accelerated toward the target (to boundary 1) in the space charge sheath. At boundary 3, the heavy particles VFD is in equilibrium shifted by flow velocity. At boundary 4, the electron beam disappears. It is assumed that Tij = Taj (j = 1, 2, 3) and vij = vaj (j = 3) (see Beilis, 1995). In general, the ion flux Γiw from the electron beam relaxation zone to the cathode is determined by a diffusion mechanism with Saha's equations for different ions at boundary 4 (see Beilis, 1995). The ion current to the cathode consists of an ion current with different ionicity which was
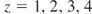
and

If the ionization-recombination length and plasma velocity are small in comparison to the length of the relaxation zone, and to the thermal velocity respectively, then Saha's equations for different ions are fulfilled in the volume of this zone.
The electron energy balance in the relaxation zone is in the form:
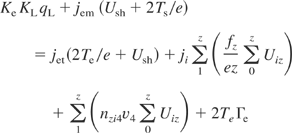
where Uiz is the potential of ionization of ions with ionicity z, fz is the ion current fraction of ions with ionicity z determined as jiz/ji, Ke is the coefficient of laser energy absorption in the relaxation zone and KL is the coefficient of whole laser energy absorption in the expanding plasma. The electron temperature is determined by the energy absorbed from the laser with power density qL and energy of emitted electrons accelerated in the sheath with potential drop Ush and energy dissipated by atom ionization, convective transport of the electrons Γe = ne4v4 and ions ni4v4 outflow through external boundary of relaxation zone. Plasma quasi-neutrality requires that ne = Σzniz, where niz is the density of ions with ionicity z = 1, 2, 3, 4, and ne is the electron density. The plasma pressure Pj = ΣnajTaj (j = 3, 4).
The target is heated by the incident ions with current density ji (bringing energy flux jiUsh) and by reverse electron with current density jet from the adjacent to the target plasma and cooled by electron emission and due to body heat conduction.
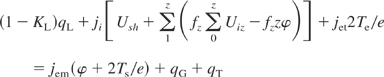
where qG is the energy loss due to target ablation, qT is the energy loss in the target body due to it heating which is obtained by the solution of the 3D heat conduction as a function of Rs (see Beilis, 1995).
The zero electrical total current at the target–plasma interface is also considered and therefore the following equation can be used:
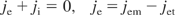
The expression for potential drop in the sheath can be obtained using Eq. (3) in the form:
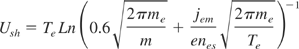
where me is the electron mass and m is the atom mass.
The rate of target ablation which is a mass flow of the ionized vapor G is obtained by
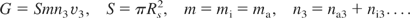
Electron emission current density is determined in the form (Beilis, 1995):
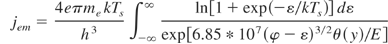
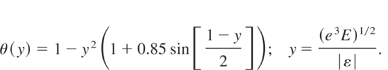
The equation for electric field at the surface target was obtained solving the Poisson equation, assuming that the volume charge is formed by positive ions flux and negative beam electron emission and back electrons from the plasma to the target:

The plasma parameters at boundary 3 serve as boundary conditions for hydrodynamic equations for mass, momentum, and energy in the expanded plasma jet. With increasing distance from the target, the plasma expands due to large plasma pressure, and the velocity V of the plasma increases in the jet. The plasma is accelerated by the thermal mechanism in which the enthalpy of the particles is transformed into kinetic energy.
The integral form of jet momentum equation
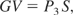
and the jet energy equation
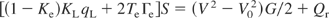
is determined by the ion velocity V of the accelerated jet, by the plasma pressure P3 at boundary 3 and spot area S (Beilis, 2003). Here Γe is the electron flux density flowing from the electron beam relaxation zone into the plasma jet expansion region and Qr is the energy loss by the radiation (Bogaerts et al., 2003).
The case when the characteristic gas dynamic time is much shorter than that for solid thermal diffusion time is considered, and therefore the plasma parameters in the transition period are determined by the target heating time (Anisimov et al., 1971). The above mentioned system of equations, taking into account the heavy particle flow in the kinetic layer, was solved to study the target ablation. In the above formulation, the spot radius Rs and laser power density qL were the given parameters. The plasma density n, Te, Ts, ji, jem, jet, αiz, Ush, E, V, Ker, and other spot parameters were calculated. An example of the calculation is presented below, showing the contribution of plasma heat flux in target heating, rate of target ablation and plasma density.
3. RESULTS
As an example, the calculations were provided for Cu target. The given parameters were: spot radius Rs = 100 μm; the coefficient which characterized the radiation absorption in plasma of expanding jet KL, for simplicity in most of the calculations, was chosen constant as 0.4, and the coefficient which characterized the radiation absorption in plasma of electron beam relaxation zone Ke was chosen as 10% of KL (Bogaerts et al., 2003; Chen & Bogaerts, 2005). It will be indicated also for other coefficients when the influence of Ke and KL on the calculated result was studied. Pulse duration t was varied as 10 ms, 1 μs, 10, 1 ns. The laser radiation intensity density qL was assumed to be constant during the laser pulse and varied in a wide range (10−3-1) GW/cm2. It was considered also that qL was close to the minimal intensity for which the solution of the system of equations can be found, i.e., when the laser plasma can be created.
The calculation shows that the potential drop in the sheath Ush decreased with qL (Fig. 2) and it is larger for lower pulse duration varying from 2 to 25 V. The electrical field at the target surface E is also larger for lower pulse duration (Fig. 3), but the dependence on laser power density is non-monotonic and a maximum of E is calculated for some certain qL determined by t. This electric field can be very large, more than 10 MV/cm. The target temperature increases with qL (Fig. 4) and decreases with pulse duration when a lower range of qL was used. For shorter pulse duration, the rate of temperature increase is larger. The electron emission current density dependence (Fig. 5) is in accordance with temperature dependence, i.e., jem also increases with qL and decreases with pulse duration for a lower range of qL. For each pulse duration, jem sharply increases with qL (growing by about 105–106 times) in the beginning, and then the rate of this increase significantly decreases with qL. At the same time, the ion current density to the target (Fig. 6) grows significantly smaller with qL for each pulse duration (by about 10–15 times), and saturated to some certain value with laser power increasing.

Potential drop in the near surface sheath as a function on laser power density.

Electric field at the target surface as a function on laser power density.

Surface target temperature T0 vs. laser power density.

Electron current density dependence on laser power density.

Ion current density dependence on laser power density.
Figure 7 shows that the electron temperature sharply decreases to a relatively small certain value and then weakly changes with qL. Te can reach up to about 5 eV for short laser pulse duration (∼ 1 ns). Similarly to Te, the degree of plasma ionization depends on qL (Fig. 8), and plasma passed from weakly ionized (α ∼ 0.01) to fully ionized state when Te increases to a few eV. In the fully ionized state, the plasma also consists of two and three charge ions. The different fractions of high charge ions (αi1 for Cu+, αi2 for Cu++, αi3 for Cu+++) as dependence on laser power density is represented in Figure 9 for laser pulse duration 10 ns. It can be seen that the high charge ions appear mainly for qL = (0.09–0.12) GW/cm2 and for qL >0.12 GW/cm2 the plasma consists mostly of one charge ions.

Plasma electron temperature vs. laser power density.

Degree of atom ionization dependence on laser power density.

Fraction of ion charge state as a function on laser power density.
The calculation shows that the plasma flow is sub-sonic near the target surface in the dense part of the plasma jet. This fact is characterized by the dependence of normalized velocity at the external boundary of the Knudsen layer b3 = v3(m/kT3)0.5 on the laser power (Fig. 10). Parameter b3 increases with qL indicating that plasma flows with velocity smaller than the ion thermal velocity by a factor less than 10−2. As a consequence, the parameter Ker also increases with qL (Fig. 11). The degree of vapor non-equilibrium near the target surface is characterized by normalized heavy particle density at the external boundary of the Knudsen layer n30 = n3 /n0. The dependence of n30 on laser power density is presented in Figure 12. It can be seen that this parameter decreases, increasing the degree of vapor non-equilibrium with qL. The heavy particle density increases by a factor of about 104 with qL increasing the target ablation in ranges for each laser pulse duration (Fig. 13). This same dependence is calculated for target ablation rate in g/s (Fig. 14).

Normalized plasma velocity at the Knudsen layer b3 = v3(m/kT3)0.5 dependence on laser power density.

Fraction Ker dependence on laser power density.

Normalized heavy particle density n30 = n3/n0 as a function on laser power density.

Heavy particle density as a function on laser power density.

Target ablation rate in g/s as a dependence on laser power density.
The calculation shows that the jet velocity decreases with qL for constant KL because an increase of the target ablation rate (see Fig. 14, KL = 0.4). In the case of KL ≠ const this velocity depends on the energy absorbed in the plasma expanding region and characterized by KL. Therefore, the jet velocity was calculated as a function of laser power density with given KL as parameter. The solution presented in Figure 15 indicated that the velocity increases with KL. In order to compare the measured rate of target ablation, the calculations also taken in account the change of KL. The dependencies of target ablation rate per pulse vs. full pulse energy density (Fig. 16) demonstrate good agreement between the measured by Caridi et al. (2006) and calculated results when KL changed with pulse energy in accordance with dependence shown in Figure 16 (Ke = 0.05).

Plasma jet velocity, V, vs. absorption coefficient KL for 10 ns laser pulse duration and Ke = 0.1.

Cu target ablation rate per pulse time measured by Caridi et al. (2006) and that calculated by the present model as a function on pulse energy density (left axis) and corresponding KL dependence (right axis) used in the calculation (Ke = 0.05).
To understand the plasma contribution by its interaction with the target, the calculation provided, considering only laser irradiation, and with addition energy flux generated in the electron beam relaxation zone. The obtained results indicate significant difference of all calculated parameters in both mentioned approaches. To demonstrate the plasma contribution in the target heat regime, the target temperature Tq was calculated considering only laser irradiation, i.e., neglecting the heat flux from the plasma by the ions and energy flux to the plasma by the electron emission. Figure 17 shows the calculation of Tq and T0 as a function of pulse energy density for condition presented in Figure 16. The difference between T0 and Tq is in region of 300–3000° C. The calculations show that this difference substantially depends on the coefficient of energy absorption in the electron beam relaxation region Ke. Figure 18 shows the calculation for Tq and T0 as a function of the coefficient of energy absorption Ke with qL as a parameter. It can be seen that the difference between Tq and T0 significantly grows as Ke and qL increases. For qL = 0.2 GW/cm2, the difference between T0 and Tq reaches more than 1000° C. As a result, the rate of target ablation is also larger in comparison to that calculated without energy flux from the plasma which originated due to laser radiation absorption. This result showed that the ion energy flux contributes significantly to the target heating and reduces the critical laser power radiation when the laser plasma appears.

Target surface temperature T0 calculated taking into account the plasma energy flux for condition presented in Figure 16 (Ke = 0.05) and target temperature Tq calculated without plasma energy inflow as a function on pulse energy density (left axis) and corresponding KL dependence (right axis) used in the calculation.

Target surface temperature T0 calculated taking into account the plasma energy flux and target temperature Tq calculated without plasma energy inflow as a function for the coefficient of energy absorption Ke in the electron beam relaxation region with qL as a parameter.
4. DISCUSSION
According to the calculation with the proposed multi-parametric model, different interconnections of very complicated phenomena occur in the laser generated plasma. The most important are the phenomena at the plasma–target contact which is realized by an electrical sheath. Due to a relatively large electric field at the target surface, the ion flux from the plasma toward the target is enhanced and the enhancement of the intensity of electron emission from the target results in the Shottky effect. Additional (to the laser energy) energy fluxes are originated: (1) energy flux to the target is by accelerated ions and (2) energy flux to the adjacent plasma is by accelerated electron emission. Both energy fluxes (ion and electron emission) are generated in the sheath and are strongly dependent on the potential drop in the sheath.
The electric field at the target surface depends mainly on two parameters Ush and ji. Ush decreases while ji increases with qL in region of relatively low qL and ji saturates with qL for relatively large qL. Therefore, a maximum of electric field in the dependence on qL is calculated. The plasma for sufficiently high qL mostly consists of one charge ions. However, the ion charge state dramatically changed for the low region of qL (at the minimal qL) and two and even three charged ions occurred due to a sharp increase of the plasma temperature. When the laser energy is down, this potential drop increases in order to support the future plasma generation by increase of the plasma electron temperature, and as a consequence, by the degree of atom ionization growing. According to the calculation, the surface temperature decreased and therefore the vapor density decreased substantially (exponentially with T0) when the laser radiation intensity and pulse duration decreased. As a result, α increases to 1. The high rate of atom ionization supports the high level of ji and therefore the large heat flux to the target surface.
Let us discuss the dependencies of plasma parameters in the considered region of qL and t for a given absorption fraction of the incident laser power. The ion current and electron emission decrease considerably when qL decreases to the minimal value in the range considered here for qL and t. Below some critical laser irradiation qL, plasma cannot be generated because the incident laser power is sufficient only for target vaporization, and the laser irradiation interacts with the matter as an independent heat source. Above the lower critical radiation, the plasma generates additional heat flux, and the surface temperature is increased. As a result, the rate of target ablation increased in comparison to that calculated without energy flux from the plasma, which originated due to laser radiation absorption. The lower critical power was determined as a minimal laser irradiation for which the self-consistent solution of the mathematical model is absent. As a consequence, the sum of plasma heat flux and laser radiation to the target lower than the critical power cannot reproduce the plasma density, even for fully ionized vapor.
On the other hand, the heavy particle density and electron emission current density substantially increase with qL due to increase of the target temperature. Therefore, the degree of ionization is dropped with no. The electron temperature also dropped due to relatively large energy losses by the back electron current jet which increases because Ush decreased with qL. As a result, for some large critical qL the plasma cannot be reproduced due to its very low degree of ionization in the electron beam relaxation zone. The larger critical power was determined as a maximal laser irradiation for which the self-consistent solution of the mathematical model is absent. This means that the plasma heat flux and laser radiation to the target larger than the maximal critical power cannot reproduce the plasma density self-consistently by the mechanism of energy exchange in the electron relaxation region, and for relatively large qL the highly ionized plasma can be generated by the interaction of laser radiation with expanding vapor jet in region where the density is lower. In the last case, the plasma significantly shields the target and this effect can be considered as a mechanism of instability by laser-target interaction during the radiation pulse.
According to the calculation, a relatively large difference between plasma parameters, as well as between target temperatures, is obtained using the present model and model where the heat flux from the plasma by the ions and energy flux to the plasma by the electron emission were neglected. This result indicated that the plasma energy flux contributes significantly to the target heating and the laser generated plasma not only passively shields the target from the laser radiation, but also converts the absorbed laser energy to kinetic and potential energy of plasma particles, which were transported not only in the expanding plasma jet, as it was considered previously (for example, see Bogaerts et al., 2003), but also to the target surface.
The solution indicates that the plasma flow in the Knudsen layer is sub-sonic and the normalized plasma velocity b3 and the heavy particle evaporation fraction Ker are much less than a unit indicating that the heavy particle back flux is relatively large, and that the net of target evaporating flux significantly differs from the Langmuir rate of evaporation in a vacuum. This result is obtained because a relatively large back flux from the high density plasma is formed near the target surface, by high intense laser radiation and therefore the vaporization is not in a vacuum. As b3 and n0 increase, then the rate of target mass loss G increases with qL by the target evaporation. In the case of constant KL, the jet velocity V decreases because larger ablative mass was accelerated with qL due to the increase of G. On other hand, the velocity V increases with KL. The last result agrees with results calculated by Bogaerts et al. (2003) and measured plasma energy by Caridi et al. (2006) indicating the important role of laser absorption efficiency in comparison to increase of G with qL in real time dependent process. The validation of this follows also from the comparison of calculated and measured Caridi et al. (2006) the rate of target ablation as a dependence on pulse energy density.
5. CONCLUSIONS
(1) A physical model of laser plasma generation taking into account the electron emission relaxation region with self-consistent mass and energy exchange at the solid-plasma interface was developed. The plasma phenomena including creation of a space charge sheath near the target surface, the kinetics of target ablation, vapor heating, atom ionization and plasma jet expansion were considered.
(2) The plasma is heated by an additional (to the laser radiation) energy flux from the emitted electrons accelerated in the sheath and the vapor can be highly ionized. For Cu target, the ions with charge up to Cu+3 was calculated for laser power density <1 GW/cm2.
(3) Plasma–target interaction was due to incoming energy flux to the target from the adjacent plasma by the accelerated ion and back electron fluxes. The large ion current to the target was supported by a relatively large electric field at the target surface in the space charge sheath formed near the target.
(4) It was shown that the absorbed laser power in the plasma was converted into kinetic and potential energy of the plasma particles and was returned to the target. The target surface temperature calculated, taking into account the plasma energy flux, was sufficiently larger than that without this flux.
(5) The minimal and maximal laser power density was determined as values when near target plasma can be reproduced by an additional plasma energy flux to the target depending on the vapor ionization state. It was indicated that for qL lower than the maximal value, the plasma created self-consistently in the relaxation region near the target while for larger qL the plasma can be created by vapor interaction with laser radiation in the expanding vapor jet.




















