The impulsive Rayleigh–Taylor or Richtmyer–Meshkov environment (Richtmyer, 1960; Meshkov, 1969; Zabusky, 1999; Brouillette, 2002) is a common fluid configuration in supernova astrophysics, where outgoing blast and shock waves interact with interstellar “clouds” (inhomogeneities) and in laser (inertial confinement) fusion, where high power laser beams drive shock waves in solid matter and these attempt to compress and heat a confined D-T gas to nuclear reaction temperatures.

To continue to explore the physics of jets and vortices in these environments, we suggest a new laboratory configuration: the shock/hemispherical-bubble-on-wall configuration (Fig. 1), and simulate its physical properties. This configuration may be easily set up in a vertical cylindrical shock tube and also models a “reshock” environment, where a spherical bubble is symmetrically struck by two identical approaching shocks. The configuration allows us to examine vorticity deposition from the incident (right-moving) and reflected (left-moving) shocks, a coaxial upstream-moving jet, and the primary ring vortex projectile (VP) with entrained shocklets and quadrupole structure that moves ahead of the jet.

Schematic of axisymmetric computational domain and boundary conditions for the shock/hemispherical-bubble-on-wall interaction. Incident shock propagates from left to right in the z direction and reverses its direction after reflection on an ideally reflecting wall at z/r0 = 6. Boundary conditions are inflow (left) and reflecting (right) in the z direction, and reflecting (bottom) and reflecting (upper) in the r direction. SD represents the two-dimensional rectangular subdomain to calculate the circulation of the “dual” vorticity deposition. Parameter domain: Mach number = 1.2, 1.5, and 2.0; density ratio η = ρ2 /ρ1 = 5.0; specific heat ratio for both gases γ = 1.402; resolution is 840(z) × 280(r); initial bubble radius r0 is 140 zones. Both z and r coordinates are normalized by the initial radius of the bubble r0.

In our numerical study, the axisymmetric, compressible Euler equations in two dimensions are solved with the piecewise parabolic method (PPM) of Colella and Woodward (1984). We model the hemispherical bubble in air as a sharp interface (approximately 2 grid zones) with a density ratio of 5.0, which is associated with SF₆. The Figure 1 caption contains the initial conditions and simulation parameters. Both z and r coordinates are normalized by the initial radius of the bubble r₀. Time is normalized by characteristic transit time scale,

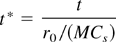
where M is Mach number of the incident shock and C_s is sound speed in the preshocked ambient air. We assume that both the pressure and density of the preshocked ambient air are normalized to be unity, that is, the isothermal sound speed in the ambient preshocked air is unity. Pressure continuity is applied across the bubble interface initially. The perfect gas equation of state is used for both gases, with an identical ratio of specific heat of 1.402. These approximations are sufficiently accurate for our relatively low Mach number studies. We study three different Mach numbers, M = 1.2, 1.5, and 2.0 and emphasize the M = 1.5 case.

Samtaney and Zabusky (1994) have quantified the primary circulation deposited by a shock passing over density-stratified interfaces at very early times. In our new configuration, the quick succession of incident and reflected shocks gives rise to almost colocated vortex layers that cancel each other as shown in Figure 2. Here we present time-dependent circulations, positive (Γ₊), negative (Γ₋), and total (Γ)

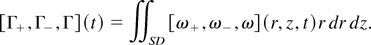
Evolution of positive, negative, and total circulation on/within the bubble (integrated over the SD domain as indicated in Fig. 1). Simulation results for the shock/hemispherical-bubble-on-wall configuration with M = 1.5. E1: negative vorticity deposition epoch, and E2: positive vorticity deposition epoch. Time is normalized by r0 /(MCs).

They are obtained by integrating ω_± and ω = ω₊ + ω₋ (where ω_± are the positive and negative components of the vorticity), over SD, a rectangular diagnostic box, chosen conveniently to surround the original half-bubble, as illustrated in Figure 1. This diagnostic box allows us to omit complex nonessential vortex processes outside the bubble that arise mainly from the r-directed shock wave and its reflection from the upper boundary.

In Figure 2, we see vorticity deposition in two epochs: E1, the familiar “negative” deposition phase and E2, the reshock “positive” deposition and cancellation phase. E2 begins when the incident shock is reflected and moves upstream. Note that the transmitted shock within the bubble is still moving toward the reflecting boundary. During the E2, the positive circulation deposition is larger because of the complex shock cavity implosion–expansion phenomenon, as discussed first by Zabusky and Zeng (1998). Note, the transmitted shock “cavity” formed within the bubble implodes before the reflected shock hits the upstream axis (after traversing the evolving bubble interface). We will study the off-bubble axis and late time circulation evolution in the near future

The collapse and reexpansion of the internal shock-bounded cavity causes the bubble to deform and begin to expand upstream along the axis while generating local clusters of vorticity In our visiometrics approach, we visualize and quantify four scalars: density, ρ; vorticity, ω; dilatation, ∇·u (to highlight wave patterns); and numerical shadowgraph, Δρ (to juxtapose contact discontinuities and shock waves). We project data to one space dimension (z) to emphasize vortex clusters and vortex projectiles (VPs) and the profile of the coaxial jet. We present r-integrated vorticity and bubble mass, γ_±(z, t) and χ(z, t)

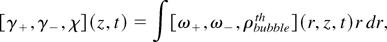
where ρ_bubble^th = ρ if ρ is larger than prescribed threshold densities 3.7, 5.0, and 9.0 (for M = 1.2, 1.5, and 2.0, respectively) and is 0 otherwise. The threshold density values are chosen so that M_b(t)/M_b0 = 0.99, where M_b(t) and M_b0 are the bubble mass and its initial value, respectively. This quantification is made after the primary reflected shock passes away from the bubble. In Figure 3, we juxtapose four different diagnostics for M = 1.5 at t* = 14.0: (a) density, (b) χ(z, t) (at t* = 6.57 and 14.0), (c) vorticity, and (d) γ_±(z, t). Vorticity is highly localized, and five compact negative vorticity regions dominate in γ_±(z, t): VP1, VP2, CV1, CV 2, and CV3. VP1 and VP2 are different strength VPs that arise, as discussed below. CV1 is a jet-precursor vortex cluster; CV 2 is a vortex cluster that drives the tip of the coaxial jet, and CV3 is a strong cluster of compact vortex regions that entrains a large amount of bubble mass. For all Mach numbers, after E2, the total kinetic energy of the jet decays slightly to near-constant values. Similarly for the total z-momentum. We summarize these results in Table 1 at t* = 14.0 for M = 1.2, 1.5, and 2.0 by presenting normalized quantities

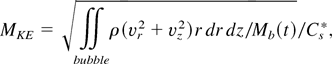
where

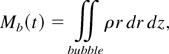
and C_s* is sound speed in reshocked ambient air. The radial flow structures on the right boundary are much weaker.

Characteristic Mach numbers of the coaxial jet for M = 1.2, 1.5, and 2.0a

a: Density, ρ; b: r-integrated jet mass, χ(z, t); c: vorticity, ω; and d: r-integrated vorticity, γ±(z, t) at normalized time t* = 14 for M = 1.5. Note: χ(z, t) is shown at another time step t* = 6.57 in b. Coherent structures are labeled.

VP1 and VP2 mentioned above arise from the vortex layer near the axis that arises at the triple point (Hornung, 1986) from the upstream reflected shock. VP1 forms from the rolled-up vortex layer, for M = 1.5 and entrains shocklets and has a quadrupole structure. These are shown by ∇·u and vorticity patterns in Figure 4 for M = 1.5. M = 1.5 is optimal because the angle between vortex layer and the z-axis is appropriately acute and the strength is moderate, so that two compact regions of vorticity, VP1 and VP2, form just behind the Mach stem. VP1 is stronger than VP2 and moves ahead of the coaxial jet with a much higher velocity, and eventually escapes from the jet. The primary entrained shocklet should be well resolved in experiment because it is perpendicular to the z-axis. For the other Mach numbers only one VP forms. For M = 1.2, the vortex layer is weaker than that for M = 1.5. For M = 2.0, the vortex layer is stronger than that for M = 1.5. However, the angle between it and the z-axis is much larger and the center of the roll-up is off the axis, thereby making the velocity of the VP smaller. Thus only one VP appears ahead of the jet.

∇·u (upper row) and vorticity ω (below) pattern (zoom in) juxtaposition for M = 1.5 at normalized times: t* = 3.14 (a), t* = 3.43 (b), t* = 3.72 (c). White region in ∇·u pattern is expansion. Coherent structure VP1 labeled in Figure 3 is circled in c.

Quantifications of VP1 and the primary entrained shocklet are given for the M = 1.5 case at t* = 10.3 in Figure 5: (a) r-integrated positive and negative vorticity γ_±(z, t) and (b) on-axis density juxtaposed with r-integrated ∇·u. The r-integrated ∇·u diagnostic is presented to emphasize the primary entrained shocklet. Because VP1 is very smooth, the shocklets' contribution to the vorticity field is unimportant. Regions of moderately compressive and expansive divergence fields are more important. The vorticity distribution of VP1 in the r-direction is obtained by taking a slice at the z-location where the r-integrated negative vorticity has its maximum magnitude (as indicated by the white line in Fig. 5a). Unlike the Hill's spherical vortex, our ω/r ∝ r².

Quantifications of VP1 at t* = 10.3 for M = 1.5: a: r-integrated positive and negative vorticity, γ±(z, t); b: on-axis density ρon-axis and r-integrated divergence of velocity, ξ = ∫∇·u dr (Left and right vertical labels are for ξ and ρon-axis, respectively). Zoom-in thumbnail images are attached: vorticity image ω at the right-bottom of a; ∇·u and Δρ images at the left-bottom and right-bottom of b, respectively.

Validation studies included an examination of the reflection boundary condition at the downstream wall and a grid refinement. For the former, we examined a one-dimensional configuration and found the velocity near the wall after reflection to be five orders of magnitude smaller than the incoming velocity. For the latter, over a range of four in refinement, the net circulation and jet phenomenology are nearly the same and the small-scale VPs differ. In a recent study of the Richtmyer–Meshkov configuration (Peng et al., 2002), we find that a small but finite interfacial transition layer can be used to obtain very good agreement between experiment and simulation for large- and intermediate-scale features.

In summary, jet and vortex flows are observed and quantified for a new proposed Richtmyer–Meshkov configuration, a shock/hemispherical-bubble-on-wall. For M = 1.5, the reflected shock is followed closely by shocklet-entrained vortex ring projectile that moves upstream ahead of the jet. The upstream moving coaxial jet, localized vortices, and vortex projectiles are ubiquitous for all Mach numbers examined (M = 1.2, 1.5, and 2.0) and the entire flow field becomes almost incompressible and vortex-dominated at late time.

We believe that this configuration provides a space-efficient environment for examining the formation of coherent vortex rings and jets by multiple shocks. The shape of the bubble can be easily controlled in a vertical shock tube either with a soap-film-surrounded gaseous bubble or a gelatin-solid bubble. We look forward to symmetry-breaking three-dimensional perturbations that will modify the outgoing jet and its associated VPs.