Published online by Cambridge University Press: 01 March 2004
Multiple ionization of large clusters when they are irradiated by an intense ultrashort laser pulse is investigated. Different mechanisms, responsible for cluster ionization, are investigated. It is found that the ionization of large clusters, irradiated by a strong intense ultrashort laser pulse, is realized by means of the surface thermoemission.
The exposure of large clusters comprising several thousand atoms or molecules to the field of a short intense laser pulse (∼100 fs long or some 30 periods of laser field) produces highly excited matter (Sullivan et al., 1996; Boehly et al., 1997). The heating of conduction electrons in the case of metal clusters or primary ionized electrons in the case of clusters of inert gas atoms on the one hand and the absence of a fast heat sink mechanism like that in an ordinary plasma on the hand allow the achievement of a state of much greater excitation of the electron subsystem as compared with the excitation of isolated atoms and molecules. In this case, atomic ions remain practically unheated. Following the fast initial multiple ionization, for the rest of the duration of the laser pulse, the matter of the cluster ion is an ideal plasma composed of electrons and multiple charged atomic ions.
There are different mechanisms of expansion pertaining to clusters of noble gases when exposed to a laser pulse (Lezius et al., 1998). The energy distribution of electrons in the exploding cluster includes electrons with kinetic energies up to 30 keV, which is several orders of magnitude greater than the energies observed in the case of above-threshold ionization of individual atoms or molecules (Delone & Krainov, 2000).
Experimental results are adequately explained by a theoretical model that regards the cluster as a small plasma sphere. The cluster is ionized by the laser field and internal collisions and then starts to expand. As the cluster expands, the electron concentration decreases and at the some point in time the frequency of the laser field comes into resonance with the frequency of the surface Mie resonance. This leads to a rapid transfer of electromagnetic (EM) energy to the electrons, causing a sharp peak in the electron temperature. At this instant the atomic ions of the cluster are vigorously stripped to high charge numbers by the hot electrons and the cluster explodes. Such collective phenomena are very important in the case of a cluster, while being absent in the event of the interaction of a laser field with individual atoms.
We consider here the models of the cluster plasma, which allows us to analyze properties of this system in the process of the production of the dense plasma by a laser pulse. These models describe the heating of the cluster when the average electron energy (i.e., electron temperature T) increases to a few kiloelectron volts and tens of kiloelectron volts, and the collision processes dominate. The electron–electron collisions establish the Maxwell distribution with an electron temperature T that grows with time. Depending on the laser intensity, the classical thermal electron energy 3T/2 can be larger or smaller than the average ponderomotive electron energy Up = F2/4ω2, where F and ω are the laser field strength amplitude and laser frequency, respectively. Here and below the atomic system of units e = me = ħ = 1 is used. The electron temperature T increases until the cluster ion begins significantly to expand.
Besides the heating, some electrons are ejected from the cluster by the laser field by means of the thermal evaporation from the surface of the cluster and by other ways (see below). Accordingly, the charge Z′ of the cluster ion increases with time during the laser pulse. We find a simple relation between the growth of the electron temperature T and the cluster ion charge Z′.
Simple estimates confirm that the cluster plasma is ideal. The condition for being an ideal plasma is NZ3 << T3, where N is the concentration of atoms in the cluster, Z is the mean charge of the typical multicharged atomic ion inside the cluster, and T is the electron temperature.
This work is organized in three sections. In Section 2 the different ionization mechanisms are studied and in Section 3 a summary and conclusion is presented.
For our analysis, we take a cluster consisting of n = 105 atoms. The kind of atoms is really unimportant at the irradiation by intense laser pulse. Let us choose Na atoms (Z = 11) and a linearly polarized laser pulse with the peak field intensity of I = 1015 Wcm−2, light frequency ω = 1 eV, and the pulse duration τ = 50 fs. Such a cluster has the radius R = 100 × 10−8 cm.
At first, the laser pulse induces a dipole excitation that causes the center of mass of the valance electron cloud to oscillate about the ionic background. The oscillations are dominated by the Mie surface plasmon whose period for Na clusters is about 1.5 fs. However, very soon these collective oscillations get perturbed because of the cluster atoms ionozation. The latter process is analogous to Landau damping, that is, the attenuation of the plasmon in an electron gas. A typical relaxation time due to Landau damping is 10 fs, roughly valid for clusters with n = 50–1000 atoms. It shrinks again ∼n−1/3 for very large values of n.
We shall assume that the collisions inside the cluster are high enough that no thermal or other gradients exist within the cluster. The electron temperature of the cluster is high during the laser pulse, of the order of T = 1 keV and uniform due to high thermal conductivity; the electron distribution is isotropie and described by a classical Maxwell distribution. Here,
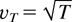
is the electron thermal velocity and vF = F/w is the field velocity. The Maxwell distribution is valid in the region of a weak laser field
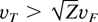
and in the region vF > ZvT of a very strong laser field (Chichkov et al., 1992).
The heating of an electron subsystem occurs mainly due to the elastic electron–ion collisions (inverse bremsstrahlung) and because of other processes as well. We will see that the atoms in the cluster are fully ionized under such conditions due to the inelastic electron–ion collisions. Then, the electron concentration is Ne = ZN where the atomic concentration for liquid Na metal is N = 2.44 × 1022 cm−3.
The thermal equilibrium is realized because time τee of electron–electron collisions is small compared to the duration τ of the laser pulse. This time can be estimated as (Silin, 1965)
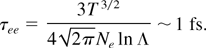
Here, ln Λ ∼ 10 is the typical value of the Coulomb logarithm. These collisions provide a further damping mechanism that drives the electron cloud toward thermal equilibrium.
We can assume that the cluster is a small plasma sphere. Such an assumption is reasonable as long as the cluster radius R is large compared with the Debye radius rD, that is, R >> rD, where the Debye screening length at T = 1 keV is
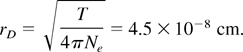
Let us first consider the internal ionization, that is, the process when electrons are removed from their host atoms but remain bound to the cluster. In the clusters, the inner ionization is produced by inelastic electron–ion collisions. The equilibrium concentration NZ of different atomic ions with the charge Z is given by the statistical Saha equation (when the equilibrium is established only by collisions; Landau & Lifshitz, 1982):
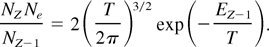
Here, EZ−1 is the ionization potential for the atomic ion with the charge Z − 1.
The condition of the total ionization of all atomic shells can be approximated in the form NZ = NZ−1 = N/2, where Z is now the nuclear charge (Z = 11 in the case of sodium atoms). Then, the hydrogen-like ionization potential EZ−1 ≈ Z2/2, and the condition of total ionization of an atom is of the form (Ne = ZN)
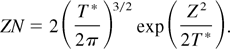
In the case of Na atoms, we obtain from this equation T* = 0.34 keV. Hence, at the electron temperature T = 1 keV, we have bare Na nuclei and electrons only. Here, T* is the temperature required for complete internal ionization. In addition to the inelastic electron–ion collisions, the internal ionization may also be produced due to the above-barrier ionization of atomic ions inside the cluster by an intense laser pulse (see below).
The results for the production of highly charged atomic states (e.g., Xe20+, Kr8+) resulting from the interaction of intense laser fields (up to ∼ 1015 Wcm−2) with atomic clusters are given (Snyder et al., 1996).
Total internal ionization inside the cluster considered in the previous subsection requires some time for its realization. This time should be less than the duration of the ultrashort laser pulse. Let us make in this subsection some estimates. The multiple ionization occurs due to the inelastic collisions of hot electrons with multicharged ions. The cross section for this process is given by the well-known simple semiempirical Lotz formula (Landau & Lifshitz, 1984):
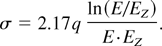
Here, E is the kinetic energy of the incident electron, Ez is the ionization potential of the atomic ion, and q is the number of electrons in the atomic shell being ionized. We use further the value of Ez = Z2/2 for hydrogen-like ions. Hence, the rate of the process in question is obtained from Eq. (5) in the form
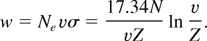
Here, v is the velocity of the incident electron, Ne is the electron concentration, and N is the concentration of atoms in the cluster (i.e., of bare nuclei in the considered case of the total ionization). The electron velocity has two components: the thermal velocity
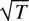
and the induced field velocity F/ω. In more typical case
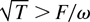
, we should average Eq. (6) over a Maxwell distribution. Assuming T << Z2/2, we find
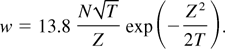
In the opposite limit
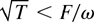
, we can simply substitute v = F/ω into Eq. (6):
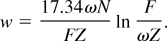
Naturally, we assumed here that the impact ionization takes place in the vicinity of the maximum of the alternating field strength F cos ωt. It should be noted that in this limit, the ionization has a threshold, and the condition F/ω > Z should be fulfilled. This condition is stronger than the above condition
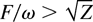
.
In the above example of T = 1 keV, laser intensity I = 1015 Wcm−2 (the field strength F = 0.166 a.u.), laser frequency ω = 1 eV, we find that the ratio
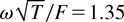
. But the value of F/ω = 4.5 < Z = 11; hence, below a threshold we have the only mechanism of thermal ionization which is determined by Eq. (7). For total ionization of the Na cluster from Eq. (7) we get w = 0.22 fs−1. Thus, electron–ion collisions occur very often during the ultrashort laser pulse.
The electromagnetic field of the laser radiation penetrates through the cluster and is damped within it. The depth of penetration δ, connected with the excitation of plasma oscillations, can be identified with the imaginary part of the wavelength inside the cluster (Krainov, 2000):
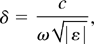
where the dielectric permittivity is
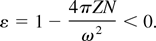
In our case of the Na cluster for the visible light we have |ε| = 370 and δ = 100 × 10−8 cm, implying that this part of damping of the laser radiation within the cluster is small. We conclude that plasma oscillations cannot be excited as a rule (except for resonance conditions).
Another part of the damping is connected with the electron–ion collisions. In τ approximation, the stationary kinetic equation for this process is of the form (at ω << νei)
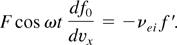
Here, f′ is the small perturbation to the equilibrium Maxwell distribution function f0 for electrons, and F and ω are the laser field strength amplitude and laser frequency, respectively. We have directed the field strength F along the axis x (the laser radiation is assumed to be linearly polarized). The rate νe of the elastic electron–ion collisions is of the well-known form (Landau & Lifshitz, 1982; see also Eq. (1))
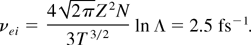
It is seen that this quantity is on order of the laser frequency ω ∼ 2 fs−1.
It should be noted that this well-known expression is valid for rapid electrons (T >> Z2). In the case of slow electrons (T << Z2), the situation is more complex (Silin, 1965). This expression is valid under the condition Zω << T3/2 only. It corresponds to the scattering of electrons on small angles. In the opposite case, Zω >> T3/2, the rate of electron–ion collisions depends on the laser frequency:
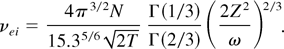
In this limit, the scattering of electrons on large angles is important, and therefore the Coulomb logarithm is absent.
We derive first the averaged energy that an electron obtains from the laser field per unit time at the condition ω << νei:
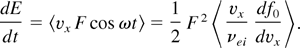
We substituted here 〈cos2 ωt〉 = 1/2. Deriving the simple integral with the Maxwell distribution f0, we find the power density Pa = NedE/dt absorbed per unit of the plasma volume:
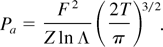
The intensity of the laser radiation I = cF2/8π decreases with the depth z of its penetration inside the cluster. The corresponding equation is of the form
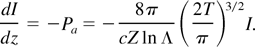
Its solution is
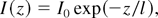
where the depth l of penetration of laser radiation inside the cluster is
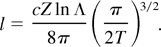
In the case of an Na cluster and a temperature of T = 1 keV, this depth is l = 1.7 × 10−8 cm. This quantity is very small compared to the cluster radius R.
In the opposite limit, ω >> νei, the power density that is absorbed within the cluster per unit of the plasma volume is given by the well-known relation of the induced bremsstrahlung at the electron–ion collisions (Fedorov, 1997):
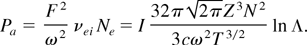
It should be noted that the quantity F2/ω2 is the energy that an electron obtains from the electromagnetic field at each collision with an ion. In this case, the penetration length of laser radiation inside the cluster is
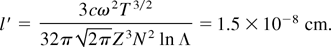
Thus, it is seen that in both limits, ω << νei and ω >> νei, the penetration length of laser radiation is very small compared to the size of the cluster. These results are valid only for homogeneous cluster plasma.
Multiple internal ionization can also be produced by the conduction electrons near the surface of the cluster which from the electromagnetic field, obtain the energy of order of the ponderomotive energy Up = F2/4ω2. This mechanism is effective in the case of long wavelength laser radiation (LaGattuta, 1998). Hence, we can conclude that the laser radiation does not penetrate deep inside the cluster and is absorbed in a thin layer on the surface of the cluster. Of course, most of the laser radiation is reflected from the cluster. Absorption is caused by the effective electron–ion collisions.
Let us now consider the ionization of the cluster, that is, the removal of electrons to infinity with the formation of a cluster ion. In the case of the metallic clusters there are conduction electrons inside the cluster. The first mechanism is the field (cold) ionization of electrons from the surface of the cluster. This process ends when the attraction of an electron to the cluster ion will be stronger than the force from the external laser field. Thus, we find, according to the Coulomb law,
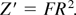
Here, Z′ is the charge of the cluster ion. In the case of laser intensity I = 1015 W/cm2 (field strength F = 8.5 × 108 Vcm−1) and R = 215 × 10−8 cm, we find Z′ = 27,200. The number of electrons released by means of this mechanism is very small compared with total number of electrons in the hot sodium cluster (the latter is Zn = 1.1 × 107). The mechanism of a Xe cluster ionization with N = 1100 atoms in a laser field of 1016 Wcm−2 was studied in a one-electron, one-dimensional approximation (Last & Joyner, 1998). The initial above-barrier ionization is realized up to the total charge of Z′ = 1200. Then, another ionization mechanism has to be responsible for the further loss of electrons. The equilibrium state of the resulting cluster ion may be regarded as a conducting sphere whose charge is located in a thin surface layer. The strong Coulomb field in this layer knocks out additional electrons from the atomic ions toward the cluster center. These electrons are accelerated to a high velocity and then leave the cluster. The Z′ = 2600 ionization becomes possible. This is the so-called ignition mechanism of ionization (Rose-Petruck et al., 1997). For example, the field at the surface of a cluster of 25 Ne atoms when all of the atoms are singly ionized is on the order of F = 5 × 1012 Vcm−1. This large field lowers the ionization barrier and enables subsequent ionization events to occur, which in turn further increases the field and lowers the ionization barrier. Hence, the fields created by the initial events “ignite” the cluster to undergo further ionization.
In the case of an inert gas cluster, the situation is rather similar to that of the metallic clusters. Of course, no conduction electrons exist within the cluster before the laser pulse. But the barrier-suppression ionization of the rare gas atoms occurs quickly at the surface of the cluster. The Bethe condition for this ionization is (Bethe & Salpeter, 1977; Brunner, 1997)
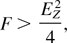
where Ez is the atomic ionization potential of an atomic ion and Z is the charge of this ion. For example, for Ne atoms (Z = 10), we find E1 = 21.5 eV, and single ionization of all atoms in the cluster takes place when the field strength reaches F = 8.0 × 108 Vcm−1. Hence, such ionization takes place very quickly (during the atomic time ∼0.01 fs). However, according to Eq. (22), the barrier-suppression ionization of the resulting Ne+ ion by such a field is impossible, because the ionization potential of this ion is E1 = 41.0 eV, and the required field strength should be F = 1.5 × 109 Vcm−1. Of course, the tunneling ionization is possible in the latter case, but it takes a very long time.
According to Eqs. (21) and (22) we find the external ionization degree Z′ of the cluster through the ignition mechanism. Eliminating the field strength F from these, one can find relations:
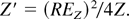
In the example of the Xe cluster with 1000 atoms, we obtain R = 25 × 10−8 cm and for total double ionization of the Xe atoms we have Z′ = 330.
The next mechanism for the electron emission from the surface of the cluster is the usual thermoemission. We use the well-known Richardson–Dushman formula for the current density of the thermoemission from the spherical surface of the cluster (Neuman, 1987; Hoyaux, 1968) in atomic units:
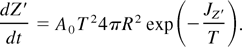
Here, A0 = 1/2π2 is the Richardson parameter. The quantity JZ′ = Z′/R is the ionization potential for the cluster ion with the charge Z′ >> 1, when the work function may be disregarded.
Integrating Eq. (24) over the laser pulse τ = 50 fs, we obtain the final charge Z′ of the cluster ion (JZ′ >> T):
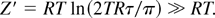
In the above case of the Na cluster, we find Z′ = 240,000. Thus, the thermoemission is a much more effective way to ionize clusters than the field (cold) ionization. With a field intensity I = 1015 Wcm−2, we find that nearly 270,000 electrons are ejected from the Na cluster with 106 atoms (1.1 × 107 electrons) during the laser pulse. This shows that the ionization degree of the cluster is very low.
The present article deals with the large clusters exposed to intense ultrashort laser pulses. The cluster is excited because of the interaction of the electron subsystem with the field of the laser pulse. Both experimental and theoretical studies of the evolution of clusters exposed to the intense ultrashort laser pulse are currently still at their initial stage.
Experimental results are adequately explained by a theoretical model that considers the cluster as a small plasma sphere. The cluster is ionized by the laser field and internal collisions, and then starts to expand. As the cluster expands, the electron concentration decreases, and at a special time the frequency of the laser field comes into resonance with the frequency of the surface Mie resonance. This leads to a rapid transfer of EM energy to the electrons, causing a sharp peak in the electron temperature. At this moment, the atomic ions of the cluster are stripped to high charge numbers by the hot electrons and the cluster explodes. Such collective phenomena are very important in the case of a cluster, while being absent in the event of the interaction of a laser field with individual atoms.
The laser field does not penetrate into the cluster, being absorbed on its surface. When the cluster explodes, however, its density is much reduced and more of the laser radiation gets into the cluster. This leads to additional internal ionization in the expanding cluster. The explosion reveals the shell structure of the clusters, so the separate layers of the cluster explode in succession. The first ions have rather large kinetic energies because of Coulomb repulsion and the efficient energy transfer from hot electrons to the outer layer of the cluster.
Different mechanisms, responsible for cluster ionization, were investigated. It was found that the ionization of large clusters, irradiated by a strong intense ultrashort laser pulse, is realized by means of the surface thermoemission. Furthermore, it was proved that the degree of ionization is low. Moreover, electron evaporation from the hot cluster surface was treated by the well-known Richardson formula, disregarding the cluster charging in the course of evaporation. In addition, the role of the cluster ion surface in the electron heating was studied and it was shown that elastic reflection of electrons takes place due to the large charge of the cluster ion, caused by the strong external ionization. Further analysis showed that the plasma oscillation cannot be excited as a rule except for resonance conditions. Moreover, taking into account ionization mechanisms, it was concluded that the laser radiation does not penetrate deep inside the cluster due to the strong absorption at its surface in a thin layer. This means that electrons absorb the electromagnetic energy in the course of the elastic collisions with ions.