Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T06:55:11.396Z Has data issue: false hasContentIssue false
  • English
  • Français

Ion jet generation in the ultraintense laser interactions with rear-side concave target

Published online by Cambridge University Press:  17 June 2010

Bin Liu ,
Hua Zhang ,
Li-Bin Fu ,
Yu-Qiu Gu ,
Bao-Han Zhang ,
Ming-Ping Liu ,
Bai-Song Xie ,
Jie Liu  and
Xian-Tu He
Bin Liu
Affiliation:
Center for Applied Physics and Technology, Peking University, Beijing, People's Republic of China Graduate School, China Academy of Engineering Physics, Beijing, People's Republic of China
Hua Zhang
Affiliation:
Center for Applied Physics and Technology, Peking University, Beijing, People's Republic of China Institute of Applied Physics and Computational Mathematics, Beijing, People's Republic of China
Li-Bin Fu
Affiliation:
Center for Applied Physics and Technology, Peking University, Beijing, People's Republic of China Institute of Applied Physics and Computational Mathematics, Beijing, People's Republic of China
Yu-Qiu Gu
Affiliation:
Fusion Research Center, Chinese Academy of Engineering Physics, Mianyang, Sichuan Province, People's Republic of China
Bao-Han Zhang
Affiliation:
Fusion Research Center, Chinese Academy of Engineering Physics, Mianyang, Sichuan Province, People's Republic of China
Ming-Ping Liu
Affiliation:
School of Information Engineering, Nanchang University, Nanchang, People's Republic of China
Bai-Song Xie
Affiliation:
College of Nuclear Science and technology, Beijing Normal University, Beijing, People's Republic of China
Jie Liu*
Affiliation:
Center for Applied Physics and Technology, Peking University, Beijing, People's Republic of China Institute of Applied Physics and Computational Mathematics, Beijing, People's Republic of China
Xian-Tu He
Affiliation:
Center for Applied Physics and Technology, Peking University, Beijing, People's Republic of China Institute of Applied Physics and Computational Mathematics, Beijing, People's Republic of China
*
Address correspondence and reprint requests to: Jie Liu, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China. E-mails: liu_jie@iapcm.ac.cn; steelan_liu@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

In this paper, the ion jet generation from the interaction of an ultraintense laser pulse and a rear-side concave target is investigated analytically using a simple fluid model. We find that the ion expanding surface at the rear-side is distorted due to a strong charge-separation field, and that this distortion becomes dramatic with a singular cusp shown on the central axis at a critical time. The variation of the transverse ion velocity and the relative ion density diverge on the cusp, signaling the emergence of an on-axis ion jet. We have obtained analytical expressions for the critical time and the maximum velocity of the ion jet, and suggested an optimum shape for generating a collimated energetic ion jet. The above theoretical analysis has been verified by particle-in-cell (PIC) numerical simulations.

Keywords

Ion accelerationIon jetTarget-normal sheath accelerationUltrashort ultraintense laser
Type
Research Article
Information
Laser and Particle Beams , Volume 28 , Issue 2 , June 2010 , pp. 351 - 359
Copyright
Copyright © Cambridge University Press 2010

1. INTRODUCTION

The advent of ultrashort ultraintense laser pulses led to the development of new exciting fields in laser plasma interaction (Karsch et al., Reference Karsch, Habs, Schatz, Schramm, Thirolf, Meyer-ter-Vehn and Pukhov1999; Malka et al., Reference Malka and Fritzler2004; Roth et al., Reference Roth, Brambrink, Audebert, Blazevic, Clarke, Cobble, Geissel, Habs, Hegelich, Karsch, Ledingham, Neelz, Ruhl, Schlegel and Schreiber2005; Mangles et al., Reference Mangles, Walton, Najmudin, Dangor, Krushelnick, Malka, Manclossi, Lopes, Carias, Mendes and Dorchies2006; Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Yu et al., Reference Yu, Xu, He, Yu, Ishiguro, Zhang and Wong2005; Glowacz et al., Reference Glowacz, Hora, Badziak, Jablonski, Cang and Osman2006; Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006; Lifshitz et al., Reference Lifshitz, Faure, Glinec, Malka and Mora2006; Sakai et al., Reference Sakai, Miyazaki, Kawata, Hasumi and Kikuchi2006; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007; Hora, Reference Hora2007; Dromey et al., Reference Dromey, Bellei, Carroll, Clarke, Green, Kar, Kneip, Markey, Nagel, Willingale, McKenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2009; Fazio et al., Reference Fazio, Neri, Ossi, Santo and Trusso2009; Hoffmann Reference Hoffmann2008a, Reference Hoffmann2008b; Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Nicolai, Stenz, Tikhonchuk, Kalal, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala, Klir, Kravarik, Kubes and Pisarczyk2009a, Reference Kasperczuk, Pisarczyk, Demchenko, Gus'kov, Kalal, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2009b; Laska et al., Reference Laska, Badziak, Gammino, Jungwirth, Kasperczuk, Krasa, Krousky, Kubes, Parys, Pfeifer, Pisarczyk, Rohlena, Rosinski, Ryc, Skala, Torrisi, Ullschmied, Velyhan and Wolowsk2007; Limpouch et al., Reference Limpouch, Psikal, Andreev, Platonov and Kawata2008; Malekynia et al., Reference Malekynia, Ghoranneviss, Hora and Miley2009; Sharma & Sharma Reference Sharma and Sharma2009; Izgorodin et al., Reference Izgorodin, Abzaev, Balyaev, Bessarab, Cherkesova, Chulkov, Fenoshin, Garanin, Gogolev, Golubinsky, Ignat'ev, Irinichev, Lachtikov, Morovov, Nazarov, Nikolaev, Pepelyaev, Pinegin, Rojz, Romaev, Solomatina, Vasin and Veselov2009; Li et al., Reference Li, Liu, Cheng, Xu, Ge and Wen2009; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Navid and Zobdeh2009; Hong et al., Reference Hong, He, Wen, Du, Teng, Qing, Huang, Huang, Liu, Wang, Huang, Zhu, Ding and Peng2009; Kline et al., Reference Kline, Montgomery, Rousseaux, Baton, Tassin, Hardin, Flippo, Johnson, Shimada, Yin, Albright, Rose and Amiranoff2009). The generation of energetic ion beams from laser plasma interaction is an exciting area of research with important applications ranging from medical proton therapy (Bulanov & Khoroshkov, Reference Bulanov and Khoroshkov2002), high-energy-density physics (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003), to fast ignition in inertial confinement fusion (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001). A beam of energetic ions has an almost straight trajectory while penetrating matter, as well as an excellent coupling efficiency to the nuclear fuel, and delivers its energy in a well defined volume because ions deposit most of their energy at the end of their range, forming a Bragg peak (Caruso & Pais, Reference Caruso and Pais1996). To date mainly three laser-ion acceleration mechanisms have been demonstrated, i.e., the target-normal sheath acceleration (Cowan et al., Reference Cowan, Fuchs, Ruhl, Kemp, Audebert, Roth, Stephens, Barton, Blazevic, Brambrink, Cobble, Fernández, Gauthier, Geissel, Hegelich, Kaae, Karsch, Le sage, Letzring, Manclossi, Meyroneinc, Newkirk, Pépin and Renard-Legalloudec2004), the break-out afterburner (BOA) (Yin et al., Reference Yin, Albright, Hegelich and Fernández2006; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernández2006), and the radiation pressure acceleration (RPA) (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Henig et al., Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer-ter-Vehn, Tajima, Nickles, Sandner and Habs2009).

In target-normal sheath acceleration, the ponderomotive force of the laser provides thermal clouds of electrons and a strong charge-separation field to accelerate ions. This process can be described by the model of free plasma expansion into vacuum (Mora, Reference Mora2003). The density of target-normal sheat acceleration ions is too low (usually less than the critical density n c) for many applications, such as for research in high energy-density matter (HEDM) (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003) and fast ignition (FI) (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001). To increase the density of the ion beams, the rear surface can be tailored to a spherical curvature in order to ballistically focus these protons to a small spot (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003; Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely2001). Using a spherically shaped target, a focused proton beam is produced and used to heat a smaller volume to over 20 eV, which provides a unique method for creating isochorically heated high-energy density plasma states (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003).

Based on particle-in-cell (PIC) simulations, the generation of proton beams using a target with a concave back surface was first studied by Wilks et al. (Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, Mackinnon and Snavely2001). They found that protons can be focused to a spot with high energy density. Following this work, a comprehensive study of the dependence of the maximum proton energy on different (concave) target shapes has been presented by Okada et al. (Reference Okada, Andreev, Mikado and Okubo2006), which concluded that a parabolic concave target is optimal for proton acceleration. By using a thin parabolic concave target, the maximum ion energy is greatly enhanced, and an optimum width for generating a high-quality ion bunch exists (Liu et al., Reference Liu, Wu, Xie, Liu, Wang and Yu2008). Via adding an axial filament stemming to the apex of a cone cavity (umbrella-like cavity target), it is found that instead of diverging after first focusing, as in the cone-shaped target, the protons produced from the umbrella-like target are well collimated (Ma et al., Reference Ma, Sheng, Gu, Yu, Yin, Shao, Yu and Chang2009).

In this paper, we develop a simple fluid theory based on the charge-separation field to investigate the physical mechanism behind the ion jet generation. We find that the emergence of the ion jet is accompanied by a dramatic distortion of the expanding ion surface. We have obtained analytical expressions for the time when the ion jet emerges and the maximum velocity that the ion jet acquires. Our theoretical analysis has been verified by PIC simulations. Our paper is organized as follows: In Section 2, we analyze the dynamics of concave target irradiated by laser pulse. Based on an extended ion expanding model, we present our analytical results on ion jet generation. To confirm the theoretical estimates, we carry out a 2D3V PIC simulations in Section 3. The PIC simulations show a clear signal of ion jet generation. Our theoretical analyses are supported by the simulation results. Section 4 is the conclusion.

2. THE DYNAMICS OF THE ION EXPANDING MODEL

An ultraintense laser incident on a target accelerates a large number of electrons. These electrons propagate to the rear side of the typical thin foil target and produce a charge-separation field. The ion acceleration on the rear surface could be explained by the model of self-similar plasma expansion into vacuum (Mora, Reference Mora2003). In the expansion process, an ion layer with thickness of the Debye length λD on the ion expanding surface is accelerated by a time-dependent charge-separation field. Now we focused on the dynamics of the thin layer. In contrast to previous work (Mora, Reference Mora2003), we extend our analysis to a 2D configuration, and the laser is propagates along x direction. Essentially, the charge-separation field E f on the layer is position-independent, pointing normal to the rear surface.

The ion expansion is commonly described by the simple self-similar, isothermal, fluid model (Mora, Reference Mora2003; Fuchs et al., Reference Fuchs, Antici, D'humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pépin and Audebert2006), in which the electrostatic charge-separation field is given by

(1)
E_{\,f}\simeq {\sqrt{2/e}E_{0} \over \sqrt{1 + \tau^2}}\comma

where $E_{0} = \sqrt{n_{e0}k_{B}T_{h}/\epsilon_{0}}\comma \; \tau = \omega_{\,pi}^{2}\lpar t - t_{0}\rpar ^{2}/\lpar 2e\rpar$, and $\omega_{\,pi} = \sqrt{Zq^{2}n_{e0}/m_{i}\epsilon_{0}}$ is the ion plasma frequency, with e being the exponential constant, m i being the ion mass, q being the electron charge, ε0 being the electric permittivity, Z being the charge number, T h and n e0 the are temperature and density of the hot electrons that drive the rear-surface expand, t 0 is the time when the rear surface begins to expand. Then the equations of motion for an element on the layer become

(2)
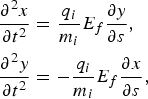
\eqalign{{\partial^2 x \over \partial t^2} &= {q_i \over m_i} E_f {\partial y \over \partial s}\comma \; \cr {\partial^2 y \over \partial t^2} & = - {q_i \over m_i} E_f {\partial x \over \partial s}\comma \; }

where q i is the ion charge, and ds = (dx 2 + dy 2)1/2 is the length of the surface element. These equations coincide with Ott's (1972) equations.

We set the initial front surface of the target at X. We immediately see that a one-dimension-fit carried out by Mora (Reference Mora2003)

(3)
\eqalign{x_0 &= X + 2 \sqrt{2e} \lambda_{D0} \left(\tau \ln \left(\tau + \sqrt{\tau^2 + 1} \right)-\sqrt{\tau^2 + 1} + 1 \right),}
(4)
\quad\; y_{0} = s\comma

is a trivial solution, and indeed this is just the unperturbed equilibrium, where $\lambda_{D0} = \sqrt{\epsilon_{0} k_B T_h/\lpar n_{e0}q^2\rpar }$ is the Debye length when the rear surface begins to expand. The most general solution of Eq. (2) is

(5)
x = x_0 - \sum_{k\comma \sigma} \xi_x^{\sigma} \lpar k\comma \; t\rpar \cos \lpar ks + \theta_k^{\sigma}\rpar \comma
(6)
y = y_0 - \sum_{k\comma \sigma} \xi_y^{\sigma} \lpar k\comma \; t\rpar \sin \lpar ks + \theta_k^{\sigma}\rpar \comma

where ξx,yσ (k, t) satisfy

(7)
\ddot{\xi}_{x\comma y}^{\sigma} - {kq_i E_f\over m_i} \xi_{y\comma x}^{\sigma} = 0\comma

and σ labels the independent solutions of Eq. (7). By assuming E f(t) changes slow, and neglecting the oscillating and dumping roots, we look for a Wentzel-Kramers-Brillouin solution of the form

(8)
\xi_x = \xi_y = a \cosh \lpar \Phi \lpar t\rpar \rpar \comma

where $\Phi\lpar t\rpar =\vint_{t_0}^t \sqrt{kq_i E_f \lpar t^{\prime}\rpar /m_i} dt^{\prime}$, a and k denote the amplitude and circular wavenumber of the perturbation, respectively. Since the solution Eqs. (5), (6) is nonlinear (Ott, Reference Ott1972), we look at a special case for a given k component to consider the solution in more detail

(9)
\eqalign{x &= X + 2\sqrt{2e}\lambda_{D0} \left(\tau \ln \left(\tau + \sqrt{\tau^{2} + 1} \right)\right. \cr & \quad -\left. \sqrt{\tau^2 + 1} + 1\right)\cr &\quad - a \cosh \lpar \Phi\lpar t\rpar \rpar \cos ks\comma \; }
(10)
y = s-a\cosh \lpar \Phi \lpar t\rpar \rpar \sin ks.

This solution extends the expanding model by adding a 2D-perturbation to a semi-empirical/analytical 1D solution of Mora (Reference Mora2003). For arbitrary amplitudes, Eqs. (9)–(10) are actually the parametric representation of a cycloid (i.e., the path followed by a point on the surface of a rolling wheel). When t = 0 the rear-side shape of the target is set to

(11)
y = {1 \over k}\arccos \left(- {x - X \over a} \right)- a \sin \left(\arccos \left(- {x - X \over a} \right)\right).

The time evolution of the profile of the ion expanding surface is shown in Figure 1. Apparently, the above analysis is valid for ka < 1. At t = 0, when a is small, the curve is approximately sinusoidal, x ≈ X − a cos (ky); at 0 < t < t*, the sinusoidal shape has become distorted; at t = t* a cusp develops in the curve; and at t > t* the solution Eqs. (9)–(10) are not valid any more because the analytical model breaks down past the cusp. The critical time t* is solved in the following.

Fig. 1. Schematic of the time evolution of the profile of the ion expanding surface.

Now we restrict our analysis to t < t*. From Eqs. (9)–(10), we obtain the ion velocity on the expanding surface (Mora, Reference Mora2003)

(12)
\eqalign{v_{e\comma x} &= 2c_{s} \ln \left(\tau + \sqrt{\tau^2 + 1} \right)\cr &\quad - a \sqrt{kg\lpar t\rpar } \sinh \lpar \Phi\lpar t\rpar \rpar \cos ks\comma \; }
(13)
v_{e\comma y} = - a \sqrt{kg\lpar t\rpar } \sinh \lpar \Phi \lpar t\rpar \rpar \sin ks.

where g(t) = q iE f(t)/m i, and $c_s = \sqrt{Zk_B T_h /m_i}$ is the ion-acoustic velocity. The transverse velocity on the expanding surface v e,y is shown in Figure 2. Initially, the profile of the transverse ion velocity in the phase space is approximately a sinusoidal wave. With time increasing, the profile becomes more distorted. This means that the ions on the surface are focused to the central axis, which is confirmed by the following analysis.

Fig. 2. The transverse velocity on the expanding surface in the phase space by combining Eq. (10) and Eq. (13).

The ion density of the expanding surface is dependent on the velocity via the equation of continuity

(14)
{d \over dt} n_i + n_i \left({\partial v_x \over \partial x} + {\partial v_y \over \partial y} \right)= 0.

According to Eq. (13), we have

(15)
\eqalign{{\partial v_{y} \over \partial y} &= \simeq {\partial v_{e\comma y} \over \partial y} = {\partial v_{e\comma y} \over \partial s}/{\partial y \over \partial s} = \cr &=-{ka \sqrt{kg\lpar t\rpar } \sinh \left(\Phi \lpar t\rpar \right)\cos ks \over 1 - ka \cosh \lpar \Phi \lpar t\rpar \rpar \cos ks}.}

In the longitudinal direction, it is suitable to describe the expanding process by the one-dimension model. Then the ion density becomes

(16)
n_i = n_{ip} {1 - ka \cos ks \over 1 - ka \cosh \lpar \Phi \lpar t\rpar \rpar \cos ks}\comma

where n ip = 2n i0/(e(1 + τ2)) is the ion density at the expanding surface for the plane target (Mora, Reference Mora2003), n i0 = n e0/Z is the initial ion density of the sheath. There is a singularity when the denominator is zero. For s = 0, we obtain the critical time t* in the implicit form

(17)
ka \cosh \lpar \Phi \lpar t^{\ast}\rpar \rpar = 1.

This means that the ion density increases dramatically when the evolution time closes to t*.

The increase of the ion density on the central axis of the expanding surface makes the electrostatic field at this point more strong than that off the central axis (confirmed by the PIC simulation in the next section). Ions are pushed by the strong electrostatic field from the central axis of the expanding surface toward the background electrons, then an ion jet is generated, and the surface is broken and a cusp emerges. When the focusing and jet formation of ions come to balance, in the motion frame (moving together with the surface), the expanding ion surface becomes approximately steady, and the ion velocities along the surface should be approximately equal because the electrostatic field is perpendicular to the surface. This assumption is valid when the intensity of laser below relativistic regime, and the plasma could be treated as fluid. Then we predict the maximum longitudinal velocity when t > t*,

(18)
\eqalign{v & = v_{\,p} + \left. \sqrt{\left({\partial x_1 \over \partial t} \right)^2 + \left({\partial y_1 \over \partial t} \right)^2} \right\vert_{t = t^{\ast}} \cr & = v_p + a \sqrt{kg\lpar t^{\ast}\rpar } \sinh \lpar \Phi \lpar t^{\ast}\rpar \rpar,}

where

(19)
v_p = 2c_s \ln \left({\omega_{\,pi} t \over \sqrt{2e}} + \sqrt{{\omega_{\,pi}^{2}t^{2} \over 2e} + 1} \right)

is the maximum velocity of a planar target.

Simple analytical expressions can be derived from the Eqs. (17) and (18) in the asymptotic limit, τ≫1. In this limit, E f ≈ 2E 0/(ωpit), and $\Phi\lpar t\rpar =\sqrt{8kc_s} \lpar \sqrt{t} - \sqrt{t_0}\rpar$, cosh (Φ(t)) ≃ sinh(Φ(t)) ≃ exp(Φ(t))/2. Then from Eq. (17) and Eq. (18) we obtain the critical time

(20)
t^{\ast} = \left({1 \over \sqrt{8kc_s}} \ln \left({2\over ka} \right)+ \sqrt{t_0} \right)^{2}\comma

and the maximum ion velocity when t > t*

(21)
v = v_{\,p} + {4c_{s} \sqrt{1 - k^2 a^2} \over \ln \lpar {2 \over ka}\rpar }.

The above analysis is exact valid for the concave cavity shaped as Eq. (11), and it can be applied to other shapes of cavity approximately. As an example, we consider three kinds of special concave targets, circle, parabolic, and triangle, which have been discussed (Okada et al., Reference Okada, Andreev, Mikado and Okubo2006) comprehensively. The cavity are defined as 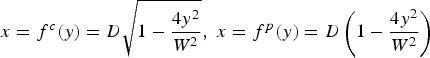$x = f^{c} \lpar y\rpar = D \sqrt{1 - {4y^2\over W^2}}\comma \; x = f^p \lpar y\rpar = D \left(1 - {4y^2\over W^2} \right)$, and $x = f^t \lpar y\rpar = D \left(1 - \left\vert {2y \over W} \right\vert \right)$, where f c, f p, f t denote circle, parabolic and triangle cavity, respectively, D is the depth and W is the diameter of the cavity. Now we expand the curve into the Fourier series. We have $a_{n} = {2\over W} \vint_{-W/2}^{W/2} f\lpar y\rpar \cos {2\pi ny \over W}$. Since the long-wavelength components tend to dominate the ion jet at long time (Ott, Reference Ott1972), we analyze the jet generation from the first order term. The first order terms are $a_{1}^{\,p\comma t} = 4D/\pi^2$ and $a_1^c = DJ_1 \lpar \pi\rpar \sim \vert a_1^{\,p\comma t} \vert$. It means that there are little differences. Then, we consider the second order terms. Since a 2t = 0, a 2p = −D/π2, and a 2c = DJ 1(2π)/2 ~ a 2p, it is less efficient to generate an ion jet from the rear-side of the trianglar concave target because of the missing second order perturbation. Hence, the maximum ion velocity of the trianglar concave target will be less than the other two kinds of targets. This simple analysis agrees with the simulation results (Okada et al., Reference Okada, Andreev, Mikado and Okubo2006).

3. PIC SIMULATION

To confirm the above estimates, we carried out our PIC simulations with the 2D3V VORPAL code (Nieter & Cray, Reference Nieter and Cray2004). The schematic drawing of our simulations is shown in Figure 3. In a simulation box of 80 × 30 µm2 with a grid of 8000 × 1500 cells, a y direction linearly polarized laser pulse with central wavelength λ = 1 µm and peak intensity I = 1.38 × 1020 Wcm−2 is incident normal onto a target along the x (axial) direction. The target density is 10n c, where n c = m eε0ω2/q is the critical plasma density, with m e the electron mass, ω = 2πc/λ the laser frequency, and c the velocity of light. The laser has a Gaussian envelope A y ~ A 0 exp [−(ρ/ρ0)2 − (t/T L)2], with spot size ρ0 = 10 µm, and pulse width L = cT L is ranging from 30 µm to 100 µm, where A 0 is the vector potential, T L denotes the laser pulse duration. The front surface of the target is located at x = 30 µm. The origin of the coordinate system is x = 0 µm, y = −15 µm. The transverse and longitudinal boundary conditions are periodic and absorbing, respectively. The target, with 30 µm in width and d = 10 µm in thickness, has a cavity on the rear surface. The geometry of the cavity is given by Eq. (11), where X = 40 µm, 2π/k = 16 µm. At the beginning of simulations, i.e., t = 0, the peak of the laser pulse is at x = −L and reaches the target surface at t 0 = 30λ/c + T L. The ion/electron mass ratio is m i/m e = 1836 and the charge number Z = 1. The transverse and longitudinal boundary conditions are periodic and absorbing, respectively. The initial electron and ion temperatures are assumed to be small and their effects can be ignored. When an ultraintense laser pulse irradiates a plasma target, the temperature of the laser-driven hot electrons T h is found numerically and experimentally to be given by the laser ponderomotive potential (Wilks et al., Reference Wilks, Kruer, Tabak and Langdon1992; Malka & Miquel, Reference Malka and Miquel1996),

(22)
k_{B} T_{h} = m_{e}c^{2} \left(\sqrt{1 + {I\lambda^2 \over 1.37 \times 10^{18}W\, \mu m^2 /cm^2}} -1 \right).

Fig. 3. Schematic drawing of the simulation box.

The total number of electrons accelerated into the target is N e = fɛL/T h, where ɛL is the laser energy, and f = 1.2 × 1015I 0.74 (Wcm2) with saturation of 0.5 is the converted fraction from laser energy to hot electrons (Key et al., Reference Key, Cable, Cowan, Estabrook, Hammel, Hatchett, Henry, Hinkel, Kilkenny, Koch, Kruer, Langdon, Lasinski, Lee, Macgowan, Mackinnon, Moody, Moran, Offenberger, Pennington, Perry, Phillips, Sangster, Singh, Stoyer, Tabak, Tietbohl, Tsukamoto, Wharton and Wilks1998; Feurer et al., Reference Feurer, Theobald, Sauerbrey, Uschmann, Altenbernd, Teubner, Gibbon, Förster, Malka and Miquel1997).

Figures 4 and 5 show that the ion density and the axial electric field E x spatial distribution at t = 90λ/c for a = 1 µm, respectively. In this simulation, the critical time is t* = 83λ/c, and hence, the figure shows the spatial distribution after the critical time. In Figure 5, a strong charge-separation field at the front of the expanding surface is clearly shown. Figure 6 presents the comparison between the electric field E x on the cental axis and that off the central axis. It is shown that the electric field on the central axis is a stronger than that off the cental axis, and the ion expanding surface is distorted by the strong electric field with a singular cusp shown on the central axis. As expected, a forward ion jet emerges from the central axis of the ion expanding surface.

Fig. 4. (Color online) The ion density spatial distribution at t = 90λ/c for a = 1 µm. It is shown that an ion jet is generated.

Fig. 5. (Color online) The axial electric field E x spatial distribution at t = 90λ/c for a = 1μm. A bright thin layer in front of the target denotes the electric field at the ion expanding surface E f.

Fig. 6. (Color online) Comparison of the axial electric field E x at t = 90λ/c for a = 1 µm. The solid (blue) line denotes the electric field on the central axis (y = 0 µm), and the dashed (red) line denotes the electric field off the central axis (y = 3μm).

Figure 7 presents the ion velocity distribution. The left column subfigures (the longitudinal velocity) show that the ions extracted from the rear-side of the target are accelerated forward. The maximum axial velocity of the ions is located at the leading edge of the expanding ion surface on the central axis represented by a sharp peak in left column subfigures. The right column subfigures (the transverse velocity) verify our theoretical analysis in Figure 2. When t = 40λ/c, the transverse velocity distribution shows a sinusoidal wave profile, while when t = 70λ/c, the profile becomes more distorted.

Fig. 7. (Color online) Time evolution and ion phase space distributions of the longitudinal (left column) and the transverse (right column) direction at t = 40λ/c (top row) and t = 70λ/c (bottom row), by simulating a concave target with a = 1μm.

Figure 8 shows the relative ion density n i/n ip as a function of time. The simulation data agree well with the theoretical results Eq. (16). Initially, the relative ion density is about one. In the region of a anticipated asymptotic value of time t max, the relative ion density increases dramatically and closes to a saturation. This means that the focusing and jet formation of ions come to balance, and the forward ion jet will persist for a long time.

Fig. 8. Relative ion density n i/n ip as a function of time for concave target with a = 1 µm. In the region of a anticipated asymptotic value of time t max, the relative ion density increases dramatically and closes to a saturation. The solid line is our analytical predict according to Eq. (16)

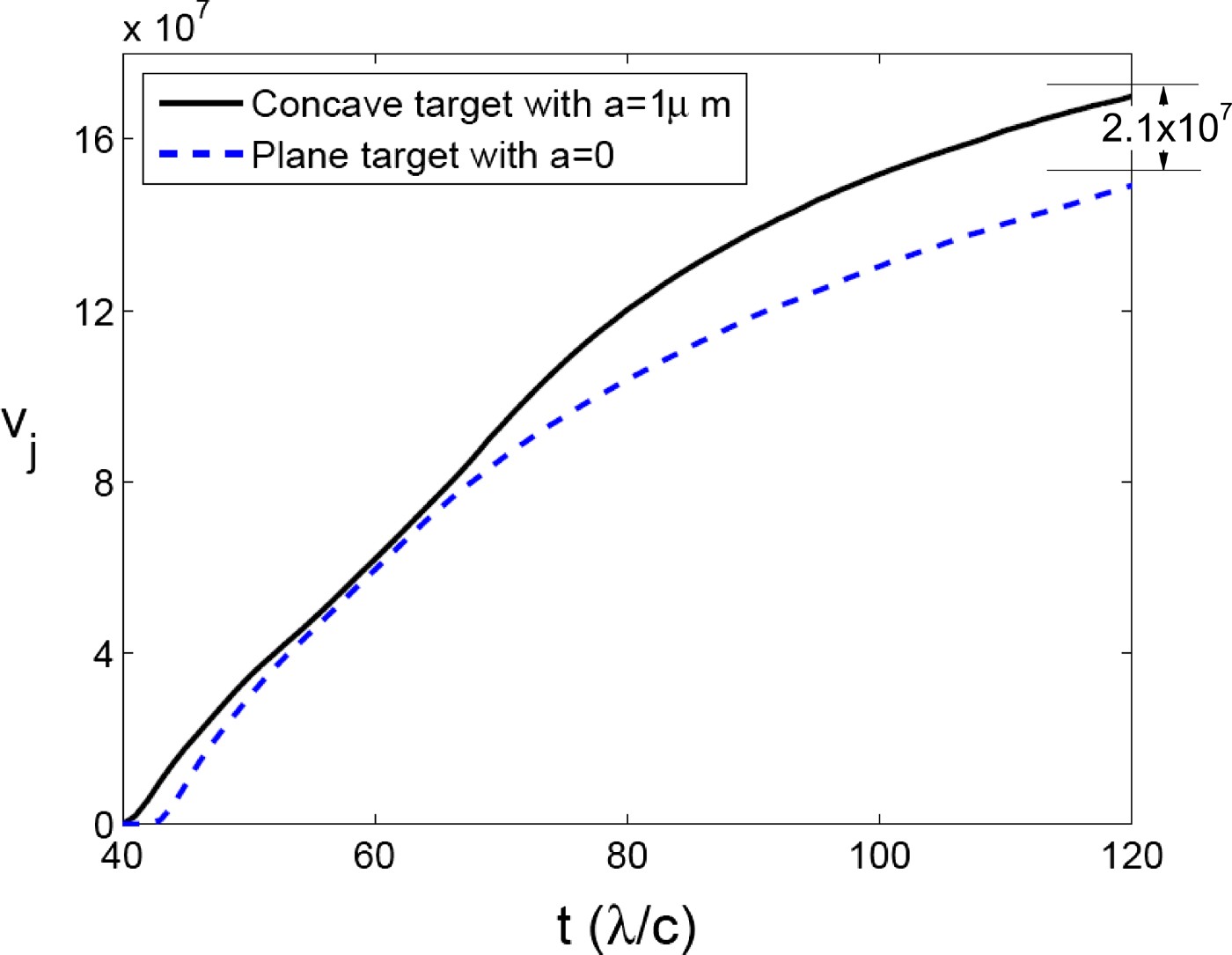
Figure 9 shows the PIC simulation results of maximum ion velocity as a function of time both for a concave target with a = 1 µm and planar target with a = 0. There is a clear indication of the post-accelerating at the time interval (60λ/c,80λ/c). Note that according to our model, when $t^{\ast}=83\lambda/c$, the post-accelerated ions form an ion jet. Our model predicts that the velocity difference between the concave and the planar target is about 1.7 × 107 m/s, close to the simulation results 2.1 × 107 m/s.

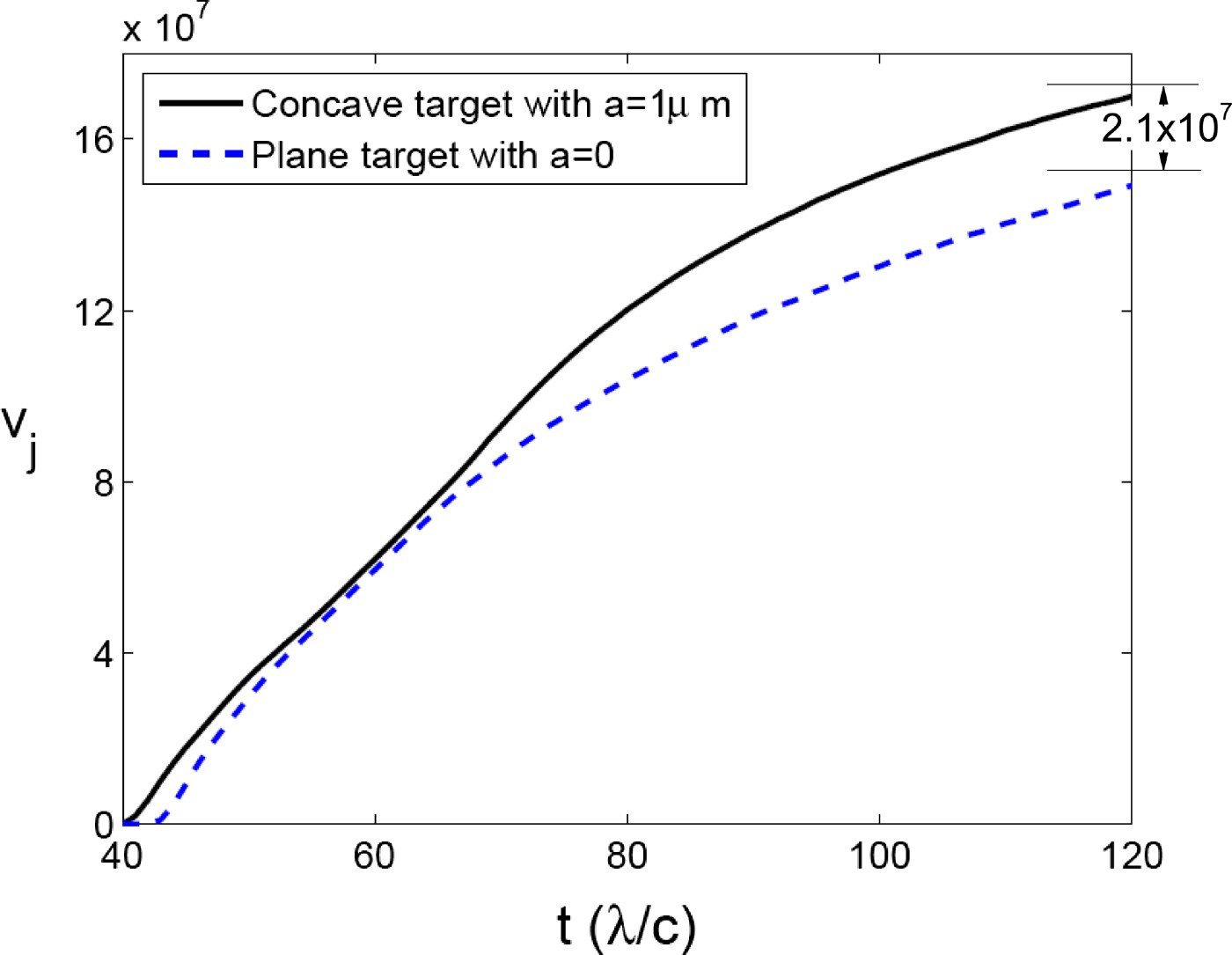
Fig. 9. The maximum velocity as a function of time for a = 1 µm.

Now we simulate the ion jet generation for different initial perturbation amplitudes a. Figure 10 shows the simulation results of the critical time for different a after irradiation by a plane-wave laser initially located at x = 0. With a increasing, the critical time decreases to t 0. In our simulation, the critical time is marked by the time when n i/n ip exceeds 10. The factor 10 is motivated by the analysis of the results described in Figure 8. Eq. (17) is solved by numerical method and the electrostatic field $E_f$ is determined by Eq. (1) as an approximation. The results of the simulation and the predicted curve according to Eq. (17) agree very well.

Fig. 10. The critical time for different aafter irradiation by a plane-wave laser initially located at x = 0. In the simulation, the critical time is marked by the time when n i/n ip exceeds 10. The factor 10 is motivated by the analysis of the results described in Figure 8.

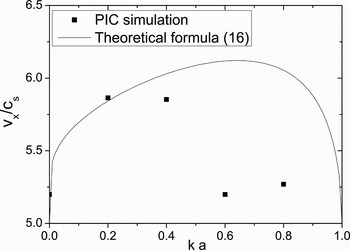
Figure 11 presents the maximum ion velocity for different a. The cut-off acceleration time is assumed to be t = 1.3T L (Fuchs et al., Reference Fuchs, Antici, D'humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pépin and Audebert2006) with pulse width L = cT L = 100 µm. There is a big difference between our prediction and simulation results when ka ~ 1. The main reason is that, for ka > 0.5, the simulation time is much greater than the jet generation time, and the ion jet will be defocused. This means that, the short-wavelength perturbations have little contribution to the collimated ion jets. Then we can conclude that, ka = 0.5 is the optimal parameter to generate the high collimated ion jet.

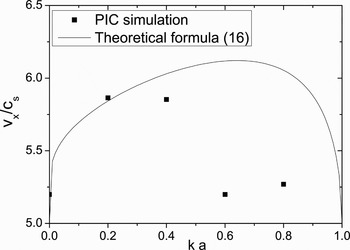
Fig. 11. The maximum velocity for different shapes. The effective acceleration time in the calculation is selected as 1.3T L with pulse width L = cT L = 100 μm.

4. CONCLUSION

In this paper, we investigated the interaction of an ultraintense laser pulse and a rear-side concave target using both a theoretical model and PIC simulations. It is shown that the emergence of an on-axis ion jet at the rear-side of the target is accompanied by a distorted, expanding ion surface. This distortion is caused by the strong charge-separation field. We presented a critical time, at which the distortion becomes dramatic with a singular cusp shown on the central axis. Meanwhile, the variation of the transverse ion velocity and the relative ion density diverge on the cusp, signaling the emergence of an on-axis ion jet. We obtained analytical expressions for the critical time and the maximum velocity of the ion jet, and suggested an optimum shape for generating a collimated energetic ion jet. Our PIC simulations support the theoretical analysis. Our results are useful in the design of target used in producing highly collimated energetic ions in high-energy-density physics.

ACKNOWLEDGMENTS

This work is supported by the National Fundamental Research Programme of China (Contact Nos.2007CB815103, 2007CB814800), the National Natural Science Foundation of China (Contact Nos. 10725521, 10875015, 10834008), and the Foundation of CAEP (Contact No. 2006Z0202).

References

REFERENCES

Bulanov, S.V. & Khoroshkov, V.S. (2002). Feasibility of using laser ion accelerators in proton therapy. Plasma Phys. Rep. 28, 453–456.CrossRefGoogle Scholar
Caruso, A. & Pais, V.A. (1996). The ignition of dense DT fuel by injected triggers. Nucl. Fusion 36, 745–758.CrossRefGoogle Scholar
Cowan, T.E., Fuchs, J., Ruhl, H., Kemp, A., Audebert, P., Roth, M., Stephens, R., Barton, I., Blazevic, A., Brambrink, E., Cobble, J., Fernández, J., Gauthier, J.-C., Geissel, M., Hegelich, M., Kaae, J., Karsch, S., Le sage, G.P., Letzring, S., Manclossi, M., Meyroneinc, S., Newkirk, A., Pépin, H. & Renard-Legalloudec, N. (2004). Ultralow emittance, Multi-MeV proton beams from a laser virtual-cathode plasma accelerator. Phys. Rev. Lett. 92, 204801.CrossRefGoogle ScholarPubMed
Dromey, B., Bellei, C., Carroll, D.C., Clarke, R.J., Green, J.S., Kar, S., Kneip, S., Markey, K., Nagel, S.R., Willingale, L., McKenna, P., Neely, D., Najmudin, Z., Krushelnick, K., Norreys, P.A. & Zepf, M. (2009). Third harmonic order imaging as a focal spot diagnostic for high intensity laser-solid interactions. Laser Part. Beams 27, 243–248.CrossRefGoogle Scholar
Esirkepov, T., Borghesi, M., Bulanov, S.V., Mourou, G. & Tajima, T. (2004). Highly efficient relativistic-ion generation in the laser-piston regime. Phys. Rev. Lett. 92, 175003.CrossRefGoogle ScholarPubMed
Fazio, E., Neri, F., Ossi, P.M., Santo, N. & Trusso, S. (2009). Ag nanocluster synthesis by laser ablation in Ar atmosphere: A plume dynamics analysis, laser and particle beams. Laser Part. Beams 27, 281–290.CrossRefGoogle Scholar
Feurer, T., Theobald, W., Sauerbrey, R., Uschmann, T., Altenbernd, D., Teubner, U., Gibbon, P., Förster, E., Malka, G. & Miquel, J.L. (1997). Onset of diffuse reflectivity and fast electron flux inhibition in 528-nm-laser-solid interactions at ultrahigh intensity. Phys. Rev. E 56, 4608–4614.CrossRefGoogle Scholar
Fuchs, J., Antici, P., D'humières, E., Lefebvre, E., Borghesi, M., Brambrink, E., Cecchetti, C.A., Kaluza, M., Malka, V., Manclossi, M., Meyroneinc, S., Mora, P., Schreiber, J., Toncian, T., Pépin, H. & Audebert, P. (2006). Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2, 48–54.CrossRefGoogle Scholar
Glowacz, S., Hora, H., Badziak, J., Jablonski, S., Cang, Y. & Osman, F. (2006). Analytical description of rippling effect and ion acceleration in plasma produced by a short laser pulse. Laser Part. Beams 24, 15–22.CrossRefGoogle Scholar
Hegelich, B.M., Albright, B.J., Cobble, J., Flippo, K., Letzring, S., Paffett, M., Ruhl, H., Schreiber, J., Schulze, R.K. & Fernández, J.C. (2006). Laser acceleration of quasi-monoenergetic MeV ion beams. Nat. 439, 441–444.CrossRefGoogle ScholarPubMed
Henig, A., Steinke, S., Schnürer, M., Sokollik, T., Hörlein, R., Kiefer, D., Jung, D., Schreiber, J., Hegelich, B.M., Yan, X.Q., Meyer-ter-Vehn, J., Tajima, T., Nickles, P.V., Sandner, W. & Habs, D. (2009). Radiation-pressure acceleration of ion beams driven by circularly polarized laser pulses. Phys. Rev. Lett. 103, 245003.CrossRefGoogle ScholarPubMed
Hoffmann, D.H.H. (2008 a). Laser interaction with matter and heavy ion fusion. Laser Part. Beams 26, 509–510.Google Scholar
Hoffmann, D.H.H. (2008 b). Laser matter interaction and related conferences. Laser Part. Beams 26, 137–138.Google Scholar
Hong, W., He, Y., Wen, T., Du, H., Teng, J., Qing, X., Huang, Z., Huang, W., Liu, H., Wang, X., Huang, X., Zhu, Q., Ding, Y. & Peng, H. (2009). Spatial and temporal characteristics of X-ray emission from hot plasma driven by a relativistic femtosecond laser pulse. Laser Part. Beams 27, 19–26.CrossRefGoogle Scholar
Hora, H. (2007). New aspects for fusion energy using inertial confinement. Laser Part. Beams 25, 37–45.CrossRefGoogle Scholar
Izgorodin, V.M., Abzaev, F.M., Balyaev, A.P., Bessarab, A.V., Cherkesova, I.N., Chulkov, V.U., Fenoshin, D.Y., Garanin, S.G., Gogolev, V.G., Golubinsky, A.G., Ignat'ev, Y.V., Irinichev, D.A., Lachtikov, A.E., Morovov, A.P., Nazarov, V.V., Nikolaev, G.P., Pepelyaev, A.P., Pinegin, A.V., Rojz, I.M., Romaev, V.N., Solomatina, E.Y., Vasin, M.G. & Veselov, A.V. (2009). Target technology development for the research of high energy density physics and inertial fusion at the RFNC-VNIIEF. Laser Part. Beams 27, 657–680.CrossRefGoogle Scholar
Karsch, S., Habs, D., Schatz, T., Schramm, U., Thirolf, P.G., Meyer-ter-Vehn, J. & Pukhov, A. (1999). Particle physics with petawatt-class lasers. Laser Part. Beams 17, 565–570.CrossRefGoogle Scholar
Kasperczuk, A., Pisarczyk, T., Nicolai, P.H., Stenz, C.H., Tikhonchuk, V., Kalal, M., Ullschmied, J., Krousky, E., Masek, K., Pfeifer, M., Rohlena, K., Skala, J., Klir, D., Kravarik, J., Kubes, P. & Pisarczyk, P. (2009 a). Investigations of plasma jet interaction with ambient gases by multi-frame interferometric and X-ray pinhole camera systems. Laser Part. Beams 27, 115–122.CrossRefGoogle Scholar
Kasperczuk, A., Pisarczyk, T., Demchenko, N.N., Gus'kov, S.Y., Kalal, M., Ullschmied, J., Krousky, E., Masek, K., Pfeifer, M., Rohlena, K., Skala, J. & Pisarczyk, P. (2009 b). Experimental and theoretical investigations of mechanisms responsible for plasma jets formation at PALS. Laser Part. Beams 27, 415–427.CrossRefGoogle Scholar
Kawata, S., Kong, Q., Miyazaki, S., Miyauchi, K., Sonobe, R., Sakai, K., Nakajima, K., Masuda, S., Ho, Y.K., Miyanaga, N., Limpouch, J. & Andreev, A.A. (2005). Electron bunch acceleration and trapping by ponderomotive force of an intense short-pulse laser. Laser Part. Beams 23, 61–67.CrossRefGoogle Scholar
Key, M.H., Cable, M.D., Cowan, T.E., Estabrook, K.G., Hammel, B.A., Hatchett, S.P., Henry, E.A., Hinkel, D.E., Kilkenny, J.D., Koch, J.A., Kruer, W.L., Langdon, A.B., Lasinski, B.F., Lee, R.W., Macgowan, B.J., Mackinnon, A., Moody, J.D., Moran, M.J., Offenberger, A.A., Pennington, D.M., Perry, M.D., Phillips, T.J., Sangster, T.C., Singh, M.S., Stoyer, M.A., Tabak, M., Tietbohl, G.L., Tsukamoto, M., Wharton, K. & Wilks, S.C. (1998). Hot electron production and heating by hot electrons in fast ignitor research. Phys. Plasmas 5, 1966–1972.CrossRefGoogle Scholar
Kline, J.L., Montgomery, D.S., Rousseaux, C., Baton, S.D., Tassin, V., Hardin, R.A., Flippo, K.A., Johnson, R.P., Shimada, T., Yin, L., Albright, B.J., Rose, H.A. & Amiranoff, F. (2009). Investigation of stimulated Raman scattering using a short-pulse diffraction limited laser beam near the instability threshold. Laser Part. Beams 27, 185–190.CrossRefGoogle Scholar
Koyama, K., Adachi, M., Miura, E., Kato, S., Masuda, S., Watanabe, T., Ogata, A. & Tanimoto, M. (2006). Monoenergetic electron beam generation from a laser-plasma accelerator. Laser Part. Beams 24, 95–100.CrossRefGoogle Scholar
Laska, L., Badziak, J., Gammino, S., Jungwirth, K., Kasperczuk, A., Krasa, J., Krousky, E., Kubes, P., Parys, P., Pfeifer, M., Pisarczyk, T., Rohlena, K., Rosinski, M., Ryc, L., Skala, J., Torrisi, L., Ullschmied, J., Velyhan, A. & Wolowsk, J. (2007). The influence of an intense laser beam interaction with preformed plasma on the characteristics of emitted ion streams. Laser Part. Beams 25, 549–556.CrossRefGoogle Scholar
Li, L.M., Liu, L., Cheng, G.X., Xu, Q.F., Ge, X.J. & Wen, J.C. (2009). Layer structure, plasma jet, and thermal dynamics of Cu target irradiated by relativistic pulsed electron beam. Laser Part. Beams 27, 497–509.CrossRefGoogle Scholar
Lifshitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser-plasma accelerator. Laser Part. Beams 24, 255–259.CrossRefGoogle Scholar
Limpouch, J., Psikal, J., Andreev, A.A., Platonov, K.Y. & Kawata, S. (2008). Enhanced laser ion acceleration from mass-limited targets. Laser Part. Beams 26, 225–234.CrossRefGoogle Scholar
Liu, M.P., Wu, H.C., Xie, B.S., Liu, J., Wang, H.Y. & Yu, M.Y. (2008). Energetic collimated ion bunch generation from an ultraintense laser interacting with thin concave targets. Phys. Plasmas 15, 063104.CrossRefGoogle Scholar
Ma, Y.Y., Sheng, Z.M., Gu, Y.Q., Yu, M.Y., Yin, Y., Shao, F.Q., Yu, T.P. & Chang, W.W. (2009). High-quality MeV protons from laser interaction with umbrellalike cavity target. Phys. Plasmas 16, 034502.CrossRefGoogle Scholar
Malekynia, B., Ghoranneviss, M., Hora, H. & Miley, G.H. (2009). Collective alpha particle stopping for reduction of the threshold for laser fusion using nonlinear force driven plasma blocks. Laser Part. Beams 27, 233–241.CrossRefGoogle Scholar
Malka, G. & Miquel, L. (1996). Experimental confirmation of ponderomotive-force electrons produced by an ultrarelativistic laser pulse on a solid target. Phys. Rev. Lett. 77, 75–78.CrossRefGoogle ScholarPubMed
Malka, V. & Fritzler, S. (2004). Electron and proton beams produced by ultra short laser pulses in the relativistic regime. Laser Part. Beams 22, 399–405.CrossRefGoogle Scholar
Mangles, S.P.D., Walton, B.R., Najmudin, Z., Dangor, A.E., Krushelnick, K., Malka, V., Manclossi, M., Lopes, N., Carias, C., Mendes, G. & Dorchies, F. (2006). Table-top laserplasma acceleration as an electron radiography source. Laser Part. Beams 24, 185–190.CrossRefGoogle Scholar
Mora, P. (2003). Plasma expansion into a vacuum. Phys. Rev. Lett. 90, 185002.CrossRefGoogle ScholarPubMed
Nieter, C. & Cray, J.R. (2004). VORPAL: A versatile plasma simulation code. J. Comput. Phys. 196, 448–473.CrossRefGoogle Scholar
Okada, T., Andreev, A.A., Mikado, Y. & Okubo, K. (2006). Energetic proton acceleration and bunch generation by ultraintense laser pulses on the surface of thin plasma targets. Phys. Rev. E 74, 026401.CrossRefGoogle ScholarPubMed
Ott, E. (1972). Nonlinear evolution of the Rayleigh-Taylor instability of a thin layer. Phys. Rev. Lett. 29, 1429–1432.CrossRefGoogle Scholar
Patel, P.K., Mackinnon, A.J., Key, M.H., Cowan, T.E., Foord, M.E., Allen, M., Price, D.F., Ruhl, H., Springer, P.T. & Stephens, R. (2003). Isochoric heating of solid-density matter with an ultrafast proton beam. Phys. Rev. Lett. 91, 125004.CrossRefGoogle ScholarPubMed
Roth, M., Brambrink, E., Audebert, B., Blazevic, A., Clarke, R., Cobble, J., Geissel, M., Habs, D., Hegelich, M., Karsch, S., Ledingham, K., Neelz, D., Ruhl, H., Schlegel, T. & Schreiber, J. (2005). Laser accelerated ions and electron transport in ultra-intense laser matter interaction. Laser Part. Beams 23, 95–100.CrossRefGoogle Scholar
Roth, M., Cowan, T.E., Key, M.H., Hatchett, S.P., Brown, C., Fountain, W., Johnson, J., Pennington, D.M., Snavely, R.A., Wilks, S.C., Yasuike, K., Ruhl, H., Pegoraro, F., Bulanov, S.V., Campbell, E.M., Perry, M.D. & Powell, H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436–439.CrossRefGoogle ScholarPubMed
Sadighi-Bonabi, R., Navid, H.A. & Zobdeh, P. (2009). Observation of quasi mono-energetic electron bunches in the new ellipsoid cavity model. Phys. Rev. Lett. 27, 223–231.Google Scholar
Sakai, K., Miyazaki, S., Kawata, S., Hasumi, S. & Kikuchi, T. (2006). High-energy-density attosecond electron beam production by intense short-pulse laser with a plasma separator. Laser Part. Beams 24, 321–328.CrossRefGoogle Scholar
Sharma, R.P. & Sharma, P. (2009). Effect of laser beam filamentation on second harmonic spectrum in laser plasma interaction. Laser Part. Beams 27, 157–169.CrossRefGoogle Scholar
Wilks, S.C., Kruer, W.L., Tabak, M. & Langdon, A.B. (1992). Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1386.CrossRefGoogle ScholarPubMed
Wilks, S.C., Langdon, A.B., Cowan, T.E., Roth, M., Singh, M., Hatchett, S., Key, M.H., Pennington, D., Mackinnon, A. & Snavely, R.A. (2001). Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 8, 542–549.CrossRefGoogle Scholar
Yin, L., Albright, B.J., Hegelich, B.M. & Fernández, J.C. (2006). GeV laser ion acceleration from ultrathin targets: The laser break-out afterburner. Laser Part. Beams 24, 291–298.CrossRefGoogle Scholar
Yu, W., Xu, H., He, F., Yu, M.Y., Ishiguro, S., Zhang, J. & Wong, A.Y. (2005). Direct acceleration of solid-density plasma bunch by ultraintense laser. Phys. Rev. E 72, 046401.CrossRefGoogle ScholarPubMed
Yu, W., Yu, M.Y., Xu, H., Tian, Y.W., Chen, J. & Wong, A.Y. (2007). Intense local plasma heating by stopping of ultrashort ultraintense laser pulse in dense plasma. Laser Part. Beams 25, 631–638.CrossRefGoogle Scholar
Figure 0

Fig. 1. Schematic of the time evolution of the profile of the ion expanding surface.

Figure 1

Fig. 2. The transverse velocity on the expanding surface in the phase space by combining Eq. (10) and Eq. (13).

Figure 2

Fig. 3. Schematic drawing of the simulation box.

Figure 3

Fig. 4. (Color online) The ion density spatial distribution at t = 90λ/c for a = 1 µm. It is shown that an ion jet is generated.

Figure 4

Fig. 5. (Color online) The axial electric field Ex spatial distribution at t = 90λ/c for a = 1μm. A bright thin layer in front of the target denotes the electric field at the ion expanding surface Ef.

Figure 5

Fig. 6. (Color online) Comparison of the axial electric field Ex at t = 90λ/c for a = 1 µm. The solid (blue) line denotes the electric field on the central axis (y = 0 µm), and the dashed (red) line denotes the electric field off the central axis (y = 3μm).

Figure 6

Fig. 7. (Color online) Time evolution and ion phase space distributions of the longitudinal (left column) and the transverse (right column) direction at t = 40λ/c (top row) and t = 70λ/c (bottom row), by simulating a concave target with a = 1μm.

Figure 7

Fig. 8. Relative ion density ni/nip as a function of time for concave target with a = 1 µm. In the region of a anticipated asymptotic value of time tmax, the relative ion density increases dramatically and closes to a saturation. The solid line is our analytical predict according to Eq. (16)

Figure 8

Fig. 9. The maximum velocity as a function of time for a = 1 µm.

Figure 9

Fig. 10. The critical time for different aafter irradiation by a plane-wave laser initially located at x = 0. In the simulation, the critical time is marked by the time when ni/nip exceeds 10. The factor 10 is motivated by the analysis of the results described in Figure 8.

Figure 10

Fig. 11. The maximum velocity for different shapes. The effective acceleration time in the calculation is selected as 1.3TL with pulse width L = cTL = 100 μm.