Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T07:18:50.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Ion acceleration by short high intensity laser pulse in small target sets

Published online by Cambridge University Press:  29 June 2009

A. Andreev ,
K. Platonov  and
S. Kawata
A. Andreev*
Affiliation:
Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan SIC, Vavilov State Optical Institute, St. Petersburg, Russia
K. Platonov
Affiliation:
SIC, Vavilov State Optical Institute, St. Petersburg, Russia
S. Kawata
Affiliation:
Graduate School of Engineering, Utsunomiya University, Utsunomiya, Japan
*
Address correspondence and reprint requests to: A. Andreev, Vavilov State Optical Institute, 12 Birzhevaya line, St. Petersburg, 199064, Russia. E-mail: andreev@mbi-berlin.de
Rights & Permissions [Opens in a new window]

Abstract

Ion acceleration by short, high intensity laser pulses in sets of small targets is treated by an analytical model developed here, and by two-dimensional particle-in-cell simulations. When an intense short laser pulse illuminates a thin foil target at normal incidence, electrons in the target are accelerated by the ponderomotive force. At the rear surface of the foil they generate a strong electric field that accelerates the ions, and generates an ion beam of small divergence. Using a mass-limited small target like a droplet enhances the ion energy, but increases divergence at the same time. In this paper, a combination of several-micron targets in a periodic structure (for example, a droplet chain) is proposed in order to increase the conversion efficiency from the incident laser beam to the emergent protons. Improvement of the energy flux conversion efficiency from the laser to the ion beam at optimal conditions is demonstrated.

Keywords

Ion accelerationLaser plasmaMass limited targetsShort intense laser pulse
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 3 , September 2009 , pp. 449 - 457
Copyright
Copyright © Cambridge University Press 2009

INTRODUCTION

A high priority area of research in laser ion acceleration is the formation of quasi-monochromatic proton beams of maximal energy and minimal divergence (Mourou et al., Reference Mourou, Tajima and Bulanov2006; Chen et al., Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Andreev and Sandner2007; Singh et al., Reference Singh, Sajal and Gupta2008). Recently, it was found (Ter Avetisyan et al., Reference Ter Avetisyan, Shnurer, Kalashnikov, Nickles, Risse, Sokollik, Sandner, Andreev and Tikhonchuk2006; Ter-Avetisyan et al., Reference Ter-Avetisyan, Schnurer, Polster, Nickles and Sandner2008a, Reference Ter-Avetisyan, Shnurer, Nickles, Sokollik, Sandner, Andreev, Psikal and Tikhonchuk2008b; Zheng et al., Reference Zheng, Sheng, Peng and Zhang2005; Strangio et al., Reference Strangio, Caruso, Neely, Andreoli, Anzalone, Clarke, Cristofari, Prete, Giorgio, Murphy, Ricci, Stevens and Tolley2007) that the conversion efficiency of laser beam energy into ion beam energy, and the maximum energy of the ions, increase when mass-limited targets (MLT) are used. For example, such a target could be a droplet that is a micron size in diameter. As is well known (Fuchs et al., Reference Fuchs, Antici, d'Humieres, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyeroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2005; Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007; McKenna et al., Reference McKenna, Carroll, Lundh, Nurnberg, Markey, Bandyopadhyay, Batani, Evans, Jafer, Kar, Neely, Pepler, Quinn, Redaelli, Roth, Wahlstrom, Yuan and Zepf2008), ion acceleration in a foil target is a result of laser-produced fast electrons generating strong electric fields at the rear surface of the target, which then accelerate ions. The smearing of the electron cloud at the rear of a foil target is limited in a droplet by the small target size, and by the radiation pressure enveloping the target as a result of diffraction (Schnurer et al., Reference Schnurer, Ter-Avetisyan, Busch, Risse, Kalachnikov, Sandner and Nickles2005). This leads to an increase in the local concentration of fast electrons in the ambipolar field and, consequently, to high energies of accelerated ions. Light diffraction produces an additional surface current of fast electrons on the target rear that also increases the electron density. All these effects lead to a significant increase (a factor of four for a droplet) of the MLT ion energy compared to a foil of the same material (Limpouch et al., Reference Limpouch, Psikal, Andreev and Platonov2008). The disadvantage of MLTs and, in particular, spherical targets is a broad (almost isotropic) angular distribution of accelerated ions (Psikal et al., Reference Psikal, Tikhonchuk, Limpouch, Andreev and Brantov2008; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Andreev and Sandner2007). Enhancement of laser absorption by a target consisting of a large number of nanoscale-size components has been demonstrated (Sumeruk et al., Reference Sumeruk, Kneip, Ditmier, Symes, Churina, Belolipetski, Donnelly and Ditmire2007; Nodera et al., Reference Nodera, Kawata, Onuma, Limpouch, Klimo and Kikuchi2008; Bagchi, et al., Reference Bagchi, Kiran and Bhuyan2008). In Ter-Avetisyan et al. (Reference Ter-Avetisyan, Schnurer, Polster, Nickles and Sandner2008a, Reference Ter-Avetisyan, Shnurer, Nickles, Sokollik, Sandner, Andreev, Psikal and Tikhonchuk2008b) and Strangio et al. (Reference Strangio, Caruso, Neely, Andreoli, Anzalone, Clarke, Cristofari, Prete, Giorgio, Murphy, Ricci, Stevens and Tolley2007), it was shown specifically that an increase in the number of fairly small droplets, irregularly distributed in space, improves the characteristics of the ion beam.

In this paper, it is shown that a combination of several micron-size targets in some periodic structure (for example, a droplet chain) can lead to the achievement of a high energy and a narrow angular distribution of accelerated ions. Geometric losses of laser radiation in such a target can be small, so that the efficiency of this target can be better than for a foil of the same thickness.

ANALYTICAL MODEL

We consider the interaction of a short laser pulse (<100 fs) with an MLT, supposing that ion acceleration occurs after the laser pulse has ended. Because ion acceleration is a slow process compared to the electron circulation time in an MLT, one can use a stationary solution of a hydrodynamic equation for the electrons. This approximation results in a simple description of the electron concentration n e as a function of the potential ϕ:

(1)
n_{\rm e} \lpar {\varphi} \rpar = n_{{\rm e}0} \left({1 + {\gamma - 1 \over \gamma }{e {\varphi} \over T_{\rm eh} }} \right)^{1 \over \gamma - 1}. \eqno\lpar 1\rpar

Here, T eh is the initial electron temperature, n e0 is the initial density of fast electrons, and γ is the adiabatic constant.

This dependence implies a stationary state of fast electrons, when electrostatics equilibrates the thermal pressure. The use of Eq. (1) implies that further movement of the fast electron cloud upon target expansion should be slow as compared to the thermal velocity of the fast electrons, which is on the order of the light velocity. We have chosen the adiabatic variant of the relationship between electron density and local electrical potential ϕ as implied by analysis of the time dynamics of ion and electron distribution functions in particle-in-cell (PIC) calculations. Under our conditions, at the time of the formation of the ion beam (a significant movement of ions occurs at 150 fs) no laser field exists, and thus it cannot influence the electron temperature and keep it at a constant value. In particular, we have seen that acceleration of ions takes place in the time range from 100 to 200 fs from the start of the calculation. The numerical analysis of the fast electron distribution function has shown that during this time interval, the number of fast electrons at its energy comparable to that of the ion decreases significantly. Therefore the adiabatic equation of state for the description of hot electron gas seems to us to be more realistic than an isothermal equation for the case of an ultrashort laser pulse (<100 fs) interacting with a thin target.

The adiabatic constant in the case of two-dimensional expansion is γ = 2 and the relation of the hot electron density with its potential energy (for the Boltzmann distribution) is therefore linear:

(2)
n_{\rm e} = n_{{\rm e}0}\lpar 1 + {\rm e} \varphi /2T_{\rm eh}\rpar . \eqno\lpar 2\rpar

This fact leads to a linear Poisson equation defining the ambipolar field, and allows an analytical treatment that is no longer one-dimensional (Albright et al., Reference Albright, Yin, Hegelich, Bowers, Kwan and Fernandez2006), but two-dimensional.

Consider the Poisson equation for a laser target located along the y axis and infinitely thin along the z axis (actually it means that the target thickness is less than the Debye radius of hot electrons) at the time immediately after the laser pulse:

(3)
\Delta\varphi =- 4 \pi \lpar \rho \lpar y\comma \; z\rpar - en_{\rm e} \lpar \varphi \rpar \rpar . \eqno\lpar 3\rpar

In the case of solid-target electrons, they are accelerated by a laser pulse on the target front surface, pass through the target, emerge into the vacuum, and create a strong electric field on the target rear. Most of them return back to the target. The process then repeats on the other target side, resulting in a cloud of hot electrons circulating through the target and moving in the transverse direction with respect to the laser beam axis. On both target surfaces, positive charge spots appear and hold the surrounding hot electrons. The volume density of positive charge included in the Poisson Eq. (2), can be described as ρ(y, z) = en e0η(ξ)δ(ζ), where the dimensionless function η(ζ) describes the charge density profile in the transverse direction, and dimensionless coordinates are introduced as ξ= y/r D, ζ = z/r D. Here, $r_{\rm D}=\sqrt {T_{\rm eh} /4\pi e^2 n_{{\rm e}0} }$ is the Debye radius. Let us introduce also the normalized time, the potential, and the fast electron density as: τ = tωph, ψ = |e|ϕ/T eh, and ηe = n e/n e0, where $\omega_{\rm ph}=\sqrt {4\pi e^2 n_{{\rm e}0} /m_{\rm e} } $. The positive charge density of the target is a consequence of the plasma charge densities of ions and cold electrons: ρ(y, z) = Zen i(y, z) − en e cold(y, z). The charge density profile changes with time, but a solution of the Poisson equation contains time only as a parameter. We suppose that the time dependence of the charge density profile is contained in the normalized characteristic scale of the hot electron spot: l(τ) = L(t)/r D, so that η(ξ, τ) = η(ξ; l(τ)). From the conditions of quasi-neutrality and a fixed number of laser-produced hot electrons, one can write the following condition at τ ≫ 1:

(4)
\eta_{{\rm e}0} = \vint\limits_{- \infty}^{+ \infty}{\vint\limits_{- \infty}^{+ \infty}{\eta_{\rm e} \lpar \zeta\comma \; \xi\rpar d \zeta d \xi}} = \vint\limits_{- \infty}^{+ \infty}{\eta \lpar \xi\semicolon \; l\lpar \tau \rpar \rpar } d\xi. \eqno\lpar 4\rpar

Here $\eta_{{\rm e}0} = {4\pi e^2\, N_{\rm eh} / T_{\rm eh} L_0}\comma \; N_{\rm eh} \approx {A\varepsilon_l / \varepsilon_{\rm eh}}$ is the number of fast electrons, A is the absorption coefficient, ɛl is the laser energy, ɛeh is the energy of fast electron, and L 0 is the initial diameter of the fast electron emission at the target rear.

We suppose that the functional form of the charge distribution given at the initial time retains this form later in time. Rewriting the Poisson equation via the electron density, and taking into account Eq. (2), one can obtain the following equation:

(5)
2\left( {\partial^2 \over \partial \zeta^2} + {\partial^2 \over \partial \xi^2}\right) \eta_{\rm e} = \eta_{\rm e} - \eta\lpar \xi\semicolon \; \zeta\semicolon \; 1\rpar . \eqno\lpar 5\rpar

Consider a distribution of the positive charge density η(ξ, ς, l) to represent a chain of droplets (since we consider a two-dimensional geometry, in reality, this is a set of cylinders, rather than spheres) along the axis y, with the coordinate of the centers ξk = y k/r D and radius ξd:

(6)
\eqalign{\eta \lpar \xi\semicolon \; \varsigma\semicolon \; l\rpar & = {\eta_{\rm e0} \over 2\pi \xi_{\rm d}}\sum\limits_{{\rm k} = - \infty }^\infty {\delta \left( \sqrt {\left({\xi - \xi_{\rm k}} \right)^2+\varsigma ^2} - \xi_{\rm d} \right) } \theta \cr & \quad \times\lpar {\rm l}\lpar \tau \rpar - \left\vert \xi \right\vert \rpar /\sum\limits_{{\rm k} = - \infty }^\infty {\theta \left( {\rm l}\lpar \tau \rpar - \left\vert {\xi_{\rm k} } \right\vert \right) }}. \eqno\lpar 6\rpar

The charge density (6) is normalized as ∬ηdξdς = ηe0. The solution of Eq. (5) found by Fourier transform and limited in space at infinity is the following:

(7)
\eqalign{& \eta_e \lpar \xi \comma \; \varsigma \semicolon \; l\rpar = {\eta_{e0} \over 8\pi ^2 \xi_d}\cr & \times {\sum\limits_{k = - \infty}^\infty \vint\limits_{- \xi_d}^{\xi_d} K_0 \left(\sqrt{{\lpar \varsigma - x\rpar ^2 + \lpar \xi - \xi_k - \sqrt{\xi_d ^2 - x^2} \rpar ^2 \over 2}}\right){dx \over \sqrt {\xi_d ^2 - x^2} \theta \lpar l\lpar \tau \rpar - \left \vert \xi_k \right \vert \rpar } \over \sum\limits_{k = - \infty }^\infty \theta \lpar l\lpar \tau \rpar - \left \vert \xi_k \right \vert \rpar }}. \eqno\lpar 7\rpar

Here K 0 is the McDonald function.

The solution found for the Poisson equation corresponds to a quasi-neutrality situation, so that the electric field is zero at infinity. The return current of cold electrons attracted by the charged area violates this quasi-neutrality state and leads to spreading of the charge spot, i.e., to an increase of the function l(τ), because the tangential component of the electric field $E_y = \beta E_\xi = \beta {\partial \psi / \partial \xi}$ draws electrons from spot edge into the center according to Ohm's Law: j cold = σcoldE y, where β = T eh/r D. Then from the condition of quasi-neutrality at the expanding spot edge (ξ = l) and the law of charge conservation in the target:

dl\vint {\eta_{\rm e} \lpar \zeta\comma \; l\lpar \tau\rpar \comma \; l\lpar \tau\rpar \rpar d\zeta} + d\tau \; \vint {\,j_{\rm c} d\varsigma} = dl\vint {\eta \lpar \zeta\comma \; l\lpar \tau\rpar \comma \; l\lpar \tau \rpar \rpar } d\zeta,

one can obtain the differential equation that describes the lateral dynamics of the charged spot:

(8)
{dl \over d\tau} = {\vint \sigma_{\rm c} E_\xi \lpar \xi = l\comma \; \varsigma\semicolon \; l\rpar \; d\varsigma \over \vint {\lpar \eta \lpar \xi=l\semicolon \; \varsigma\semicolon \; l\rpar - \eta_{\rm e} \lpar \xi=l\comma \; \varsigma\semicolon \; l\rpar \rpar d\zeta}}. \eqno\lpar 8\rpar

Here, j h0 = en e0c, j c = j cold/j h0, σc = βσcold/j h0. We estimate the conductivity of the solid plasma target as $\sigma_{\rm cold} \approx {\omega_{\rm pc} / {4\pi}}$, where we neglect the influence of the magnetic field because at our conditions the gyro-frequency of a cold electron is less than its plasma frequency $\omega_{\rm pc}=\sqrt {4\pi e^2 n_{\rm ec} / {m_{\rm e}}}$. Braking of the spot expansion is connected with the redistribution of power over a large area, so the solution of Eq. (8) can be approximated by the solution of a diffusion equation at the beginning. Later, when the expansion time is comparable to the effective time of collisions 1/ν ef, the diffusion law must cease to be appropriate because the expansion exponentially decays. When modified in the light of this fact, the expansion law can be written as:

(9)
l\lpar \tau \rpar \approx \sqrt {l_0 ^2+{\kappa \over {\nu_{\rm ef} }}\left({1 - e^{ - \nu_{ef} \tau } } \right)}. \eqno\lpar 9\rpar

Here, the diffusion coefficient is $\kappa=\left. {\lim } \right\vert_{l \to \infty }{2l\vint \sigma_{\rm cold} E_\xi \lpar \xi=l\comma \; \varsigma\semicolon \; l\rpar\; d\varsigma /j_{h0} / {\vint \lpar \eta \lpar \xi=l\semicolon \; \varsigma\semicolon \; l\rpar - \eta_{\rm e} }}$${\lpar \xi=l\comma \; \varsigma\semicolon \; l\rpar \rpar d\zeta }$, where all integrals are taken over infinite intervals. The quantity νef is the effective frequency of collisions, taking into account the fact that the hot electrons spend only part of the time in the target, and part in the vacuum: νef = νeir d/2r Dωph, and νei is the collision frequency in an unbounded plasma with a non-stationary temperature and density.

To calculate the conductivity of a droplet chain that was caused by an induced dipole moment, we use a model of conducting spheres of radius r d spaced at a distance a > r d between their centers, and placed in an external electric field $\vec E$. It is known that the potential for one sphere in the external field is $\varphi \lpar \vec r\rpar = - \vec E \cdot \vec r + {r_{\rm d}^3 \vec E \cdot \vec r / {r^3}}$, where the second term is the potential of the dipole moment induced in the sphere by an external field. Thus, when a wave of polarization propagates along the droplet chain, at each step (k) denoting a droplet location, there is a change in the field value of $\delta \vec E_{{\rm k} + 1} = \lpar r_{\rm d}^3 /a^3 \rpar \vec E_{\rm k}$. The time required for such a change of the field consists of the propagation time of the field at the distance a, and time for the redistribution of electric charge in the droplet ~ωpc−1. 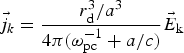Thus, the density of the polarization current $\vec j_{\rm k} \approx \delta \vec E_{\rm k} /\delta t$ can be estimated as $\vec j_k = {{r_{\rm d}^3 /a^3} \over {4\pi \lpar \omega_{\rm pc}^{- 1} + a/c\rpar}}\vec E_{\rm k} $. Therefore, the polarization conductivity of a droplet chain can be written as:

(10)
\sigma_{\rm d} \approx {{r_{\rm d}^3 /a^3 } \over {4\pi \lpar \omega_{\rm pc}^{ - 1} + a/c\rpar }}. \eqno\lpar 10\rpar

When one reduces the distance between droplets a → r d, and simultaneous reduces the time of wave propagation a/c < ωpc−1 (passage to the limit of continuum media), this result turns into the polarization conductivity of a solid target σcold. Note that the factor r d3/a 3 can be interpreted as a size factor for filling of the space by the electrons. For the a and r d values considered, the inequality ωpc−1 ≪ a/c applies, and thus the conductivity of the droplet chain is σd ≈ cr d3/4πa 4 ≪ σcold.

The model developed shows that if a droplet is located far from other droplets, then equi-potential lines are almost circles. With droplet converging toward each other, and with an increase of their numbers, we get a picture similar to a foil target. The condition of droplet convergence is that a distance between them is comparable to the Debye radius of hot electrons a ≤ r D. Even a small number of droplets with a micron distance between its edges leads to the formation of equi-potential surfaces close to planar surfaces.

As the number of ions accelerated by an ambipolar field is small compared to the total number, we will treat them as «test» particles. Then, to construct an ion distribution function dependence on ion departure angle, we should solve the equations of ion motion in the potential ψ:

(11)
{{\partial ^2 \varsigma } \over {\partial \tau ^2 }}=\delta {{\partial \psi } \over {\partial \varsigma }}\comma \; {{\partial ^2 \xi } \over {\partial \tau ^2 }}=\delta {{\partial \psi } \over {\partial \xi }} \eqno\lpar 11\rpar

where δ = m e/m i.

To calculate the case of a droplet chain, we set the normalized radius of droplet as ξd = r d/r D, and at the initial time consider homogeneously placed ions on the droplet surface. This gives the initial conditions for Eq. (11) as:

(12)
\eqalign{& \left. \xi \right\vert_{\tau=0} \,=\,\xi_0 \in \lsqb \xi_{\rm k} - \xi_{\rm d}\semicolon \; \xi_{\rm k}+\xi_{\rm d} \rsqb \cr & \left. \varsigma \right\vert_{\tau=0} \,=\,\varsigma_0=\sqrt {\xi_{\rm d}^2 - \lpar \xi_0 - \xi_{\rm k} \rpar ^2 }} \eqno\lpar 12\rpar

Here ξk = a(2k + 1)/r D is the normalized coordinate of the center of the droplet with the index k. Ion initial velocities are zero for all droplets.

As a result of solving Eq. (11) with the initial conditions (12), one can obtain the dependence of the ion velocity angle on its initial coordinate ξ0. The simulations have shown that the ion trajectory does not differ very much from a straight line at long times because of its small angle of propagation. Therefore, we employ such a simplified connection between velocity and time in the electric field argument to write the following formula for the ion propagation angle:

(13)
\theta_{\rm i} \lpar \xi_0 \rpar = {\left. \partial \xi/\partial \tau \right\vert_{\tau \to \infty} \over \left. \partial \varsigma/\partial \tau \right\vert_{\tau \to \infty}} \approx {\vint\limits_0^\infty E_\xi \lpar \xi_0\comma \; {\rm \nu}_i \lpar \xi_0 \rpar \tau\semicolon \; l\lpar \tau \rpar \rpar d\tau \over \vint\limits_0^\infty E_\zeta \lpar \xi_0\comma \; {\rm \nu}_i \lpar \xi_0 \rpar \tau\semicolon \; l\lpar \tau \rpar \rpar d\tau }\comma \; \eqno\lpar 13\rpar

where E ξ,ζ(ξ, ζ; l(τ)) = −2∂ηe(ξ, ζ; l (τ))/∂(ξ, ζ).

Let us estimate this angle at a large distance from the target. We replace the sum in Eq. (7) by an integral when there is a large number of droplets, replace the K 0 function in Eq. (7) by its asymptotic value at ς ≫ 1, and calculate this integral by the method of steepest descent. As the result, we obtain $\eta _{\rm e} \lpar \xi \comma \; \zeta \semicolon \; l\rpar \approx{1 \over {4\sqrt {2\pi } }}\eta \lpar \xi \comma \; l\rpar \exp \lpar \!-\! {\varsigma / {\sqrt 2 }}\rpar $ and, finally from Eq. (13):

(14)
\theta _{\rm i} \approx \sqrt 2 {1 \over \eta }{\partial \eta \over \partial \xi}. \eqno\lpar 14\rpar

The maximum velocity of ion initially located at the position ξ0 is determined by the maximal value of the non-stationary potential at this point:

(15)
\eqalign{{\rm \nu}_{\rm i} \lpar \xi_0 \rpar & =\sqrt {4\eta_{\rm e} \lpar 0\comma \; \xi_0\semicolon \; l\lpar H\lpar \xi_0 - l_0 \rpar \lpar \xi_0 ^2 - l_0 ^2 \rpar /\kappa \rpar } \cr &\approx \sqrt {4\eta_{\rm e} \lpar 0\comma \; \xi_0\semicolon \; \xi_0 \cdot H\lpar \xi_0 - l_0 \rpar \rpar }} \eqno\lpar 15\rpar

Here H is the Heaviside step function.

The ion angle distribution function is determined by the following formula:

(16)
{{dN_{\rm i} } \over {d\theta_{\rm i} }} \approx \rho_{\rm s}{{dl} \over {d\theta_{\rm i} }} = N_{\rm d}{{\sqrt {d\varsigma_0 ^2+d\xi_0 ^2 } } \over {d\theta_{\rm i} }}=N_{\rm d}{{\sqrt {1+{{\left({\xi_0 - \xi_{\rm k} } \right)^2 } \over {\xi_{\rm d}^2 - \left({\xi_0 - \xi_{\rm k} } \right)^2 }}} } \over {\lpar d\theta_{\rm i} /d\xi_0 \rpar }} \eqno\lpar 16\rpar

Here N i is the number of fast ions, and dl is a small part of the circle of droplet radius r d. Note that at r d → ∞ the resulting distribution function is going to the limit of a plane foil. The constant in the distribution function can be found from the normalization condition, so that N d is the number of accelerated ions from one droplet.

Let us introduce the ion angular efficiency χ ε[0;1], the total energy of the ions contained in the angle interval [+10°, −10°], as a ratio of the total energy of ions across the entire angular range; i.e.,

(17)
\chi = {{\vint\limits_0^{\xi_{10} }{d\xi_0 \sqrt {\dot \varsigma ^2+\dot \xi ^2 } \sqrt {1+{{\left({\xi_0 - \xi_{\rm k} } \right)^2 } \over {\xi_{\rm d}^2 - \left({\xi_0 - \xi_{\rm k} } \right)^2 }}} } } \over {\vint\limits_0^{\xi_{\rm d} }{d\xi_0 \sqrt {\dot \varsigma ^2+\dot \xi ^2 } \sqrt {1+{{\left({\xi_0 - \xi_{\rm k} } \right)^2 } \over {\xi_{\rm d}^2 - \left({\xi_0 - \xi_{\rm k} } \right)^2 }}} } }}\comma \; \eqno\lpar 17\rpar

where ξ10 is the initial coordinate of the ion departing from a droplet at the angle 10°.

NUMERICAL MODEL AND SIMULATION RESULTS

To verify and calibrate the analytical model developed above, the simulations of high-intensity short-laser-pulse interactions with a single droplet and with a droplet chain have been performed with the help of a modified 2D3V relativistic PIC code (Kemp & Ruhl, Reference Kemp and Ruhl2005). This parallelized code makes possible the execution of a typical run in the cluster on a node with 100 CPUs for a maximum of a few hours per simulation. The simulation geometry is shown in Figure 1.

Fig. 1. (Color online) The laser-target structure used in this paper to model an interaction of a high intensity short laser pulse with a droplet chain. The calculation area is 30 λ in both directions. There are five droplets in the chain target.

The targets contained one or two species (hydrogen or protons and C4+ ions in the ratio 1:1), and they were irradiated at normal incidence by a p-polarized laser pulse of wavelength 800 nm and a variety of intensities. The pulse had a Gaussian shape in time and a super-Gaussian (eighth degree) spatial distribution at the focal spot. To prevent numerical heating the initial plasma temperature was set to 1 keV (for the cell size λ/100 × λ/100 in the simulation box). This relatively high temperature can be justified for MLT (Psikal et al., Reference Psikal, Tikhonchuk, Limpouch, Andreev and Brantov2008). The initial electron density was 100n c, which is slightly less then solid density, to decrease computational demands. As a first example of the target, we consider a chain of five hydrogen droplets of diameter 4 µm. This target was irradiated by a laser pulse of a duration of 66 fs at an intensity 5 × 1018 W/cm2, and several different spot sizes (20, 8, 6, 4 µm). In the simulations, the plasma density profiles were sharp in space (super-Gaussian of degree 8). There were different distances between the edges of the droplets, such as: 4 µm, 1 µm, and 0 µm (the last case simulates a solid target).

The simulations have shown that the expansion of a single droplet irradiated by a high intensity laser pulse occurs almost as isotropic one. With the merging of five droplets in the chain, ion maximal energy did not change significantly, but the momentum distribution stretched in the laser direction. The ion angular distributions for different distances between droplets are shown in Figure 2 (color online).

Fig. 2. (Color online) The dependence of ion distribution on the angle in degrees for different distances between droplets. The red line is for a 4 µm gap between neighboring droplet edges, blue is for 2 µm and green for 1 µm; the black line is the analytical result for a gap of 2 µm. Here the laser spot size is 8 µm and the droplet diameter is 4 µm.

The ion angle distribution for the largest distance between droplets (4 µm) is shown by the red line, and it is almost the same distribution as the result for the single droplet. The ion angle distribution for the small distance between droplets (1 µm) is shown by the blue line and it is almost the same distribution as the result for the solid target. The green line shows the results calculated by Eq. (15) of the ion angle distribution function for five droplets with the distance between their centers of 2r D. When the distance between droplets has been increased up to 10r D, the analytical distribution becomes almost isotropic and it coincides with the simulated distribution of ions shown by the red line. Thus, our analytical model describes the effect of narrowing of the distribution by reducing the distance between droplets.

To understand the details of the interaction, we calculated the dependence of laser pulse absorption on the distance between the droplets. From Figure 3 we see that there is maximal absorption at a particular distance between droplets. Even at zero distance between droplets, one has about 20% higher absorption compared to a foil target. It is a consequence of additional absorption of laser energy from the effect of droplet curvature (Limpouch et al., Reference Limpouch, Psikal, Andreev and Platonov2008). A small droplet separation (target pieces) (Nodera et al., Reference Nodera, Kawata, Onuma, Limpouch, Klimo and Kikuchi2008) (a–r d) ≤ r E causes an increase of laser energy absorption because an electron accelerated from a droplet crosses another droplet and does not come back to the laser field like in the case of amplified spontaneous emission. A big droplet separation causes large geometric losses of laser energy, and thus a big decrease of absorption coefficient as shown in Figure 3.

Fig. 3. The dependence of laser energy absorption on the distance between droplet centers. Here, the laser spot size was 20 µm, and the droplet diameter 4 µm. The absorption coefficient is given in percent, the distance in microns.

To find the optimal target for maximal ion flux energy density, we calculated the ion angular efficiency χ for different chain parameters. As examples, the ion angular efficiency dependence on the distance between the droplet centers is shown in the following figures. The calculations show that if there is no gap between droplets (of a chain) then its maximum ion energy significantly reduces (in three times) compared to a single droplet case. In addition, the droplet chain has a narrow ion angular distribution in comparison with almost isotropic distribution of one droplet.

The reason for ion beam narrowing is a wider spot of fast electrons at the target rear and because electron conductivity for solid target in transversal direction is higher compare to a droplet chain, an electron spot is wider. The combination of these two tendencies leads to the advantage of a chain target as compared to a foil, as shown in Figure 4. Also, as one can see from Figure 4, our analytical model reproduces well the maximum of the ion angular efficiency that follows from reducing the distance between the droplets, and shows the resulting increase in the total energy of the ions contained in the angle interval.

Fig. 4. The circles are the simulated results of the dependence of ion angle efficiency on the distance between the droplet centers. Here, the laser spot size is 8 µm and the hydrogen droplets are of diameter 4 µm. The solid line is the analytical dependence of ion angle efficiency on the distance between droplets. In the model, the laser spot size is 8 µm and the droplet diameter is 4 µm as in the simulations. The temperature of hot electrons increases in the range of distances 0-1 µm according to the result of Figure 2. The initial temperature of hot electrons was T eh = 0.6 MeV as in the simulations.

We also did simulations for higher intensity and longer duration of the laser pulse interacting with a set of droplets, and obtained the increase of maximum proton energy. The simulations were performed in particular for a hydrogen solid droplet of 4 µm in diameter with a rectangular density profile, irradiated by a 133 fs laser pulse with super-Gaussian transverse distribution (eighth degree), a spot size of 10 µm, and an intensity of 1020 W/cm2.

For the single droplet, the phase distribution is again almost isotropic as for smaller laser intensity, but shows a little ion displacement in the laser direction associated with increased ponderomotive pressure. At the merging of the droplets in the chain with relatively small distance between their edges, we got a strong narrowing of the angular distribution and only a small reduction in the maximal energy as shown at the following figures.

When droplets are connected in the chain, the ion energy, as it is also for lower intensity, depends on the distance between their edges and increases as the distance increases (see Fig. 5a). However, its angular distribution (the characteristic angle of ion propagation) also increases (see Fig. 5b). Thus, regardless of the intensity at first (as one decrease the distance between droplets) narrowing of the ion angular distribution occurs, and then reduction of the maximum ion energy to the level of a foil target.

Fig. 5. (a) The dependence of ion energy (in MeV) of the droplet chain on the distance between the droplet centers. Here the chain of five hydrogen solid droplets of diameter 4 µm is irradiated by a laser pulse of duration 133 fs and intensity 1020 W/cm2. (b) The dependence of ion propagation angle (in degrees) on the distance between droplet centers for the chain of five droplets of diameter 4 µm and a laser intensity of 1020 W/cm2.

However, if for the same chain, we take the laser diameter equal to or smaller than the droplet diameter, then ion energy decreases. Accelerated ions in this case actually occur in only one droplet and the influence of neighbors is weak. The reason for this is a poor transport of electrons from the irradiated droplet to a neighboring droplet. We emphasize that the influence of neighboring droplets on the angular distribution of accelerated ions occurs when the laser beam touches the neighboring droplets. Obviously, with a narrower laser beam, there is no significant heating of electrons located beyond the radius of the beam. These electrons create a weaker field at neighboring droplets, which did not affect angular distributions of departing ions, that is, one can say that without touching of neighboring droplets, laser ion acceleration in the case of a chain of droplets does not differ from acceleration by a single droplet. In the simulations, the following dependences of ion energy of a single droplet on the laser beam width were obtained (see Fig. 6).

Fig. 6. The dependence of the maximum proton energy of a solid hydrogen droplet (in MeV) on the laser beam spot size D, where droplet diameter was D d = 4 µm with a rectangular density profile. Open squares are at laser intensity I l = 1018 W/cm2; (b) Open circles are at laser intensity I l = 1020 W/cm2.

We see that in order to increase ion energy for a laser intensity of 1018 W/cm2, one need to take a laser spot ~2 µm wider than the droplet diameter; and when the laser intensity is 1020 W/cm2, to achieve maximum ion energy one also needs a laser diameter larger than the droplet diameter. Compared with the case of lower intensity, to achieve the maximal ion energy, a wider beam spot is necessary, because of the increasing of r E is the distance propagated by the fast electron away from the droplet edge. Accordingly, a laser beam of larger diameter is needed to move fast electrons by ponderomotive pressure into the area of light shadow for increasing of the electric field that accelerates ions.

The angular efficiency reaches the maximum shown in Figure 7 due to the fact that at decreasing distance, a narrowing of the angular distribution occurs first, and then a drop in ion energy to the foil limit. The reason for the efficiency increasing on droplet convergence is the joint effect of ion emission spot expansion and changing of ion energy.

Fig. 7. Calculated ion angular efficiency for a chain of five droplets of diameter 4 µm as a function of the distance between the droplet centers at laser intensity 1020 W/cm2.

To achieve maximum ion energy, combined with low ion beam angular distribution, without big geometric losses in the case of a droplet chain is a challenge. We can combine high ion energy with good divergence of the ion beam if, for example, we fill a laser spot with droplets (with the gap between the edges not less than 0.5 µm for the intensity of 1018 W/cm2) when geometry losses offset packing droplet density (the area of droplets to the area of the laser spot). The gain in energy for this case is estimated to be by about a factor of three, so that the packing density should be more than 0.3. It is possible when the number of droplets is large. Geometric losses for the case of higher laser intensity are larger, so that one can get the maximum of energy flux density rather than the maximum of ion energy.

Note that we considered sharp droplet edges. Changing of a sharp laser spatial profile to a normal Gaussian distribution immediately reduces the maximum ion energy for separated droplets and for a chain as well. This effect (Andreev et al., Reference Andreev, Sonobe, Kawata, Miyazaki, Sakai, Miyauchi, Kikuchi, Platonov and Nemoto2006) is connected with a reduction of the magnitude of the accelerating electric field for an ion density gradient on the border of MLT.

Ion acceleration in multi-species targets of uniform composition has been theoretically described (Tikhonchuk et al., Reference Tikhonchuk, Andreev, Bochkarev and Bychenkov2005; Brantov et al., Reference Brantov, Tikhonchuk, Klimo, Romanov, Ter-Avetisyan, Schnurer, Sokollik and Nickles2006). At the beginning of acceleration, light ions and heavy ions from the target rear are accelerated independently and, because of a different charge-to-mass ratio, a spatial separation develops. Only protons from a layer of a few Debye lengths at the target rear can be accelerated, as carbon ions from the outer layer shield the electric field formed by fast electrons. These protons are separated spatially and in energy distribution from the rest of the target. They are accelerated by the sheath electric field and explode in space due to Coulomb repulsion. This explosion is partly compensated by the electric field of heavy ions, which are located behind the protons. The fastest protons are accelerated by electric fields, created both by fast electrons and protons themselves. They form an energetic tail in the proton spectrum. The slower protons, which are located in the bunch rear, feel an additional electric field created by the expanding heavy ions. These ions create a peak in the spatial proton distribution. The peak in the proton energy spectrum of a droplet target corresponds to the plateau in the phase space. After some time, under the action of the Coulomb field some protons overtake others, producing a fine structure of the peak (Brantov et al., Reference Brantov, Tikhonchuk, Klimo, Romanov, Ter-Avetisyan, Schnurer, Sokollik and Nickles2006). In the case of droplets, the number of protons in the peak is relatively small compare to a foil, and fine structure is not observed in the simulations. This is due to high angular divergence, which leads to a lower density of fast protons, so that the effect of space charge decreases and the peak evolves more slowly in time.

Calculations for a chain of CH droplets with the same laser plasma parameters have shown a similar peak of the proton energy spectrum (see Fig. 8). Thus one can say that besides the enhanced energy flux of fast ions, such a target is also interesting as a mono-energetic proton source.

Fig. 8. Proton energy spectra for a CH droplet chain at 400 fs after interaction. The laser pulse duration is 50 fs, the spot size is 8 λ and the intensity is 4.5×1019 W/cm2. The target is a set of CH plasma cylinders of density 5n c, with diameter 4 λ and the distance λ between its edges.

CONCLUSION

It has been shown that a combination of several micron-size targets in some geometrical configuration (for example, a droplet/wire chain) can combine high energy and the narrow angular distribution of ions accelerated by a fs laser pulse of relativistic intensity. Geometric losses of laser radiation in such a target can be small, so that the efficiency of this target can be better than a foil target of the same thickness. The most efficient target for ion generation by a laser beam with a circular spot could be a target consisting of a grid of droplet nodes with a packing density greater than 0.5. For a stretched (ellipsoidal) laser beam spot, an optimum shape of the target could be a droplet chain.

ACKNOWLEDGEMENTS

This work was partly supported by the JSPS (Japan Society for the Promotion of Science), MEXT (Ministry of Education, Culture, Sports and Technology), ILE Osaka University, and CORE (Center for Optical Research and Education) in Utsunomiya University. This research was also supported in part by the EU Grant (Marie Curie) (No. PIIF-GA-2008-221727). The authors thank Professor K. Tachibana, Professor K. Mima, Professor Q. Kong, Professor P. Wang, Dr. O. Klimo, and Professor J. Limpouch for their variable discussions and suggestions on this subject.

References

REFERENCES

Albright, B.J., Yin, L., Hegelich, B.M., Bowers, K.J., Kwan, T.J.T. & Fernandez, J.C. (2006). Theory of laser acceleration of light-ion beams from interaction of ultrahigh-intensity lasers with layered targets. Phys. Rev. Lett. 97, 115002–115007.CrossRefGoogle ScholarPubMed
Andreev, A.A., Sonobe, R., Kawata, S., Miyazaki, S., Sakai, K., Miyauchi, K., Kikuchi, T., Platonov, K. & Nemoto, K. (2006). Effect of a laser pre-pulse on fast ion generation in the interaction of ultra-short intense laser pulse with a limited mass foil target. Plasma Phys. Contr. Fusion 48, 1605–1619.CrossRefGoogle Scholar
Bagchi, S., Kiran, P.P. & Bhuyan, M.K. (2008). Hotter electrons and ions from nano-structured surfaces. Laser Part. Beams 26, 259–264.CrossRefGoogle Scholar
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–168.CrossRefGoogle Scholar
Brantov, A.V., Tikhonchuk, V.T., Klimo, O., Romanov, D., Ter-Avetisyan, S., Schnurer, M., Sokollik, T. & Nickles, P. (2006). Quasi-mono-energetic ion acceleration from a homogeneous composite targets by an intense laser pulse. Phys. Plasmas 13, 122705–122715.CrossRefGoogle Scholar
Chen, Z.L., Unick, C., Vafaei-Najafabadi, N., Tsui, Y.Y., Fedosejevs, R., Naseri, N., Masson-Laborde, P.E. & Rozmus, W. (2008). Quasi-monoenergetic electron beams generated from 7 TW laser pulses in N-2 and He gas targets. Laser Part. Beams 26, 147–155.CrossRefGoogle Scholar
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Fuchs, J., Antici, P., d'Humieres, E., Lefebvre, E., Borghesi, M., Brambrink, E., Cecchetti, C., Kaluza, M., Malka, V., Manclossi, M., Meyeroneinc, S., Mora, P., Schreiber, J., Toncian, T., Pepin, H. & Audebert, P. (2005). Laser proton scaling lows and new paths towards energy increase. Nat. phys. doi:10.1038/nphys199.1-7Google Scholar
Kemp, A.J. & Ruhl, H. (2005). Multispecies ion acceleration of laser irradiated water droplets. Phys. Plasmas 12, 033105–033115.CrossRefGoogle Scholar
Limpouch, J., Psikal, J., Andreev, A.A. & Platonov, K. (2008). Enhanced ion acceleration from mass limited targets. Laser Part. Beams 26, 1–10.CrossRefGoogle Scholar
McKenna, P., Carroll, D.C., Lundh, O., Nurnberg, F., Markey, K., Bandyopadhyay, S., Batani, D., Evans, R.G., Jafer, R., Kar, S., Neely, D., Pepler, D., Quinn, M.N., Redaelli, R., Roth, M., Wahlstrom, C.G., Yuan, X.H. & Zepf, M. (2008). Effects of front surface plasma expansion on proton acceleration in ultraintense laser irradiation of foil targets. Laser Part. Beams 26, 591–597.CrossRefGoogle Scholar
Mourou, G., Tajima, T. & Bulanov, S. (2006). Optics in the relativistic regime. Rev. Mod. Phys. 78, 309–371.CrossRefGoogle Scholar
Nickles, P.V., Ter-Avetisyan, S., Schnuerer, M., Sokollik, T., Andreev, A. & Sandner, W. (2007). Review of ultrafast ion acceleration experiments in laser plasma at Max Born Institute. Laser Part. Beams 25, 347–363.CrossRefGoogle Scholar
Nodera, Y., Kawata, S., Onuma, N., Limpouch, J., Klimo, O. & Kikuchi, T. (2008). Improvement of energy conversion efficiency from laser to proton beam in a laser foil interaction. Phys. Rev. E 78, 046401–046407.CrossRefGoogle Scholar
Psikal, J., Tikhonchuk, V.T., Limpouch, J., Andreev, A.A. & Brantov, A.V. (2008). Ion acceleration by femtosecond laser pulses in small multispecies targets. Phys. Plasmas 15 053102–053110.CrossRefGoogle Scholar
Schnurer, M., Ter-Avetisyan, S., Busch, S., Risse, E., Kalachnikov, M.P., Sandner, W. & Nickles, P. (2005). Ion acceleration with ultrafast laser driven water droplets. Laser Part. Beams 23, 337–343.CrossRefGoogle Scholar
Singh, K.P., Sajal, V. & Gupta, D.N. (2008). Quasi-monoenergetic GeV electrons from the interaction of two laser pulses with a gas. Laser Part. Beams 26, 597–604.CrossRefGoogle Scholar
Strangio, C., Caruso, A., Neely, D., Andreoli, P.L., Anzalone, R., Clarke, R., Cristofari, G., Prete, E.D., Giorgio, G., Murphy, C., Ricci, C., Stevens, R. & Tolley, M. (2007). Production of multi-MeV per nucleon ions in the controlled amount of matter mode (CAM) by using causally isolated targets. Laser Part. Beams 25, 85–91.CrossRefGoogle Scholar
Sumeruk, H., Kneip, S., Ditmier, T., Symes, D., Churina, I., Belolipetski, A., Donnelly, T. & Ditmire, T. (2007). Control of laser field coupling to electrons in solid targets with wavelength scale spheres. Phys. Rev. Lett. 98, 045001–045005.CrossRefGoogle ScholarPubMed
Ter Avetisyan, S., Shnurer, M., Kalashnikov, M., Nickles, P., Risse, E., Sokollik, T., Sandner, W., Andreev, A. & Tikhonchuk, V. (2006). Quasimonoenergetic deutron bursts produced by ultraintense laser pulses. Phys. Rev. Lett. 96, 145006–145011.CrossRefGoogle ScholarPubMed
Ter-Avetisyan, S., Schnurer, M., Polster, R., Nickles, P.V. & Sandner, W. (2008 a). First demonstration of collimation and monochromatisation of a laser accelerated proton burst. Laser Part. Beams 26, 637–642.CrossRefGoogle Scholar
Ter-Avetisyan, S., Shnurer, M., Nickles, P., Sokollik, T., Sandner, W., Andreev, A., Psikal, J. & Tikhonchuk, V. (2008 b). Laser proton acceleration in a water spray target. Phys. Plasmas 15, 083106–083114.CrossRefGoogle Scholar
Tikhonchuk, V., Andreev, A., Bochkarev, S. & Bychenkov, V. (2005). Ion acceleration in short-laser-pulse interaction with solid foil. Plasma Phys. Contr. Fusion 47, B869–B878.CrossRefGoogle Scholar
Zheng, J., Sheng, Z.M., Peng, X.Y. & Zhang, J. (2005). Energetic electrons and proton generated from the interaction of ultrashort laser pulses with microdroplet plasmas. Phys. Plasmas 12, 113105–113115.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) The laser-target structure used in this paper to model an interaction of a high intensity short laser pulse with a droplet chain. The calculation area is 30 λ in both directions. There are five droplets in the chain target.

Figure 1

Fig. 2. (Color online) The dependence of ion distribution on the angle in degrees for different distances between droplets. The red line is for a 4 µm gap between neighboring droplet edges, blue is for 2 µm and green for 1 µm; the black line is the analytical result for a gap of 2 µm. Here the laser spot size is 8 µm and the droplet diameter is 4 µm.

Figure 2

Fig. 3. The dependence of laser energy absorption on the distance between droplet centers. Here, the laser spot size was 20 µm, and the droplet diameter 4 µm. The absorption coefficient is given in percent, the distance in microns.

Figure 3

Fig. 4. The circles are the simulated results of the dependence of ion angle efficiency on the distance between the droplet centers. Here, the laser spot size is 8 µm and the hydrogen droplets are of diameter 4 µm. The solid line is the analytical dependence of ion angle efficiency on the distance between droplets. In the model, the laser spot size is 8 µm and the droplet diameter is 4 µm as in the simulations. The temperature of hot electrons increases in the range of distances 0-1 µm according to the result of Figure 2. The initial temperature of hot electrons was Teh = 0.6 MeV as in the simulations.

Figure 4

Fig. 5. (a) The dependence of ion energy (in MeV) of the droplet chain on the distance between the droplet centers. Here the chain of five hydrogen solid droplets of diameter 4 µm is irradiated by a laser pulse of duration 133 fs and intensity 1020 W/cm2. (b) The dependence of ion propagation angle (in degrees) on the distance between droplet centers for the chain of five droplets of diameter 4 µm and a laser intensity of 1020 W/cm2.

Figure 5

Fig. 6. The dependence of the maximum proton energy of a solid hydrogen droplet (in MeV) on the laser beam spot size D, where droplet diameter was Dd = 4 µm with a rectangular density profile. Open squares are at laser intensity Il = 1018 W/cm2; (b) Open circles are at laser intensity Il = 1020 W/cm2.

Figure 6

Fig. 7. Calculated ion angular efficiency for a chain of five droplets of diameter 4 µm as a function of the distance between the droplet centers at laser intensity 1020 W/cm2.

Figure 7

Fig. 8. Proton energy spectra for a CH droplet chain at 400 fs after interaction. The laser pulse duration is 50 fs, the spot size is 8 λ and the intensity is 4.5×1019 W/cm2. The target is a set of CH plasma cylinders of density 5nc, with diameter 4 λ and the distance λ between its edges.