Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T15:17:29.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Interconnection between hydro and PIC codes for fast ignition simulations

Published online by Cambridge University Press:  01 March 2004

H. SAKAGAMI  and
K. MIMA
H. SAKAGAMI
Affiliation:
Computer Engineering, Himeji Institute of Technology, Himeji, Hyogo, Japan
K. MIMA
Affiliation:
Institute of Laser Engineering, Osaka University, Suita, Osaka, Japan
Rights & Permissions [Opens in a new window]

Abstract

Relativistic laser–plasma interaction, subsequent superhot electron transport, superhot electron energy deposition, and the overall implosion process are key subjects for fast ignition. All these phenomena couple with each other, and more studies by simulations are essential. We have a plan to simulate the whole of fast ignition self-consistently with four individual codes. Four codes are integrated into one big system in the Fast Ignition Integrated Interconnecting code project. In a first stage of this project, we integrate the Arbitrary Lagrangian Eulerian (ALE) hydro code with the collective particle in cell (PIC) code. The PIC code obtains density profile at maximum compression from the ALE hydro code to introduce imploded plasma into a PIC system, and we can simulate interaction between ignition laser and realistic plasma. We have evaluated reflected laser spectrum and electron energy distribution, and found many differences between the realistic plasma profile and the conventional one in PIC simulations.

Keywords

Fast ignition; Hydro code; InterconnectionPIC code; Simulation
Type
International Conference on the Frontiers of Plasma Physics and Technology
Information
Laser and Particle Beams , Volume 22 , Issue 1 , March 2004 , pp. 41 - 44
Copyright
2004 Cambridge University Press

1. INTRODUCTION

We must consider overall fluid dynamics of the implosion, laser–plasma interaction, and superhot electron generation, superhot electron transport to the target core, and superhot electron energy deposition within the core to prove fuel burning in the fast ignition scheme. These phenomena are coupled to each other and both time and space scales are much different. Each range of physical quantities that should be considered in the respective phenomena also varies in a large way. Thus it is impossible to simulate all phenomena with one code, and we must simulate each phenomenon with individual codes and integrate them in the Fast Ignition Integrated Interconnecting code project. A typical density profile in the fast ignition scheme and responsible parts for each code are shown in Figure 1a.

The concept of the Fast Ignition Integrated Interconnecting code (FI3) project. a: A typical density profile in the fast ignition scheme. Each code has responsibility for the indicated areas. b: The code integration diagram. Specified physical quantities should be communicated between codes.

A space scale varies in a wide range and the target is consecutively deformed during the implosion process. First, we should introduce an Arbitrary Lagrangian Eulerian (ALE) hydro code (Nagatomo et al., 2001) to calculate overall fluid dynamics The ALE hydro code should also include absorption of implosion lasers. Second, a collective particle in cell (PIC) code (Sakagami & Mima, 2001) must be used to simulate the generation of superhot electrons with the plasma profile that is determined by the ALE hydro code, and to get their distribution functions, because the traditional PIC code is not applicable to such a dense plasma (more than 100 times critical density). As the target core becomes 105 times solid density at maximum compression, it is impossible to compute up to this range even with the collective PIC code. We should, therefore, introduce a hybrid code in which superhot electrons are treated as a particle and background electrons as a fluid (Taguchi et al., 2001). The hybrid code receives the distribution function of superhot electrons from the PIC code and the density profile from the ALE hydro code, and calculates their transport into the target core. As the superhot current is on the order of 100–1000 MA (Honda et al., 2000), return current electrons become too warm and should not be treated as at the same temperature as cold background electrons. Thus we should employ two temperatures of electron fluids for return current and background. This hybrid approach, however, has uncertainty about the return current temperature and density of both fluids. In our code integration, the hybrid code can get not only the distribution function of superhot electrons but also the temperatures and densities for both return current and background fluids from the PIC code to solve this ambiguous problem. It is noted that temperatures for two fluids and return current electron density are assumed to be constant for simplicity. As the surface connection between the hybrid and PIC codes usually causes numerical errors, we would install a volume connection scheme between them. Finally, a Fokker–Planck code (Johzaki et al., 2001) is used to compute their energy deposition and to estimate the fuel burning. The electric field in the Fokker–Planck code is determined by assuming current neutrality (Bell et al., 1998), and we can take into account deceleration of superhot electrons due to this electric field. A code integration diagram and physical quantities that should be communicated between codes are shown in Figure 1b. Physical quantities with solid arrows are primary data that should be transferred between codes as the law of causality, and those with shaded arrows govern feedback that can be neglected according to simulation circumstances.

2. INTERCONNECTION

If we integrate four individual codes into one big one, it is very hard to maintain this code because separate teams at different sites have been developing each code and this approach is never realistic. Additionally, we cannot run this code efficiently on a single parallel computer system, because computation grains of each code are very different and parallel performance is strongly degraded. Thus we will run the code individually at each site, collaborating with each other with data transfer via the computer network. As each code can be independently executed, we can select the appropriate architecture for the computers, such as vector supercomputers, symmetrical multiprocessor type parallel computers, or massive parallel scalar computers, to run the code. Because communication in our project is very straightforward and not complex, we design a lightweight communication protocol (Distributed Computing Collaboration Protocol) to transfer data between codes and implement two kinds of daemon programs. One of them is called Communicator, and it actually transfers data instead of the code itself, and the other is called Arbitrator, and it manages communication between Communicators. The code only asks the Communicator, which runs in the background at its site, to send data to another code, and then the Communicator passes data to another remote Communicator corresponding to the code that should be received data via the Internet. Finally that code receives the data from the local Communicator. If a broadband dedicated line is available between Communicators, the Arbitrator tells both Communicators to use that dedicated line instead of the Internet, and high-speed communication can be done even though both codes do not know about details of network connections. This concept is shown in Figure 2a as the code communication chart, and the summary of the Distributed Computing Collaboration Protocol is shown in Figure 2b.

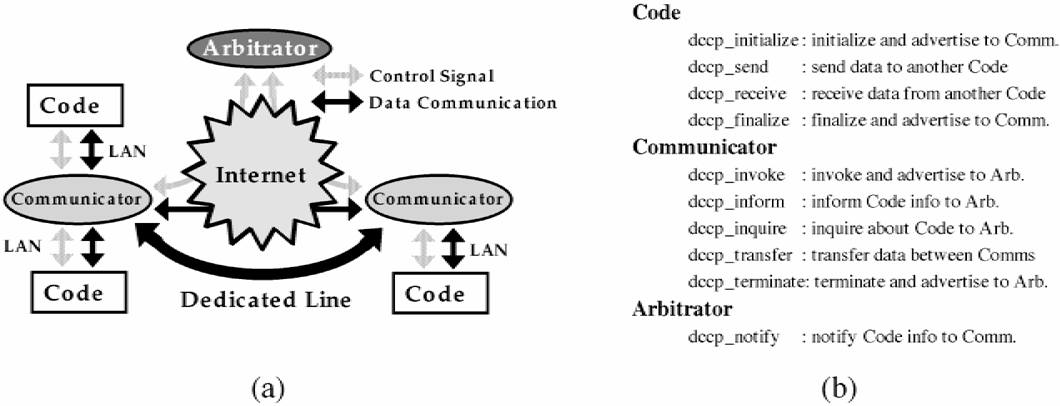
Distributed Computing Collaboration Protocol. Communication chart (a) and summary of protocol (b).

In a first stage of the project, we integrated the ALE hydro code with the collective PIC code. The collective PIC code obtains density profile at maximum compression from the ALE hydro code and introduces imploded plasma into the PIC system. Then an ultrahigh intense ignition laser is launched into the plasma, and we can simulate laser–plasma interaction in a realistic situation. As a low-density corona plasma is too long to simulate with the PIC code, we must cut the plasma at an appropriate point. Parametric instabilities produced by laser–plasma coupling, such as stimulated Raman scattering, however, predominantly occur within this underdense plasma, and the ignition laser may lose its energy before reaching dense plasma. Thus the thickness of the underdense plasma can affect an energy conversion ratio from the ignition laser to superhot electrons and could be an important factor for fast ignition simulations. We introduced two cases: (1) cut the plasma at 0.1 ncr with 25 μm underdense plasma and (2) cut the plasma at 0.05 ncr with 55 μm. On the other hand, we cut the profile at 100 ncr to avoid difficulty in computing the ultradense plasma with the PIC algorithm. We gradually increase the number of electrons per mesh to track the obtained density profile up to 200 electrons per mesh at twice critical density. In the overdense region, we preserve the number of electrons to 200 per mesh but increase a collective factor to fit the profile. We also introduced other typical profiles that are mostly used in PIC simulations, namely the linear profile and the flattop profile, to evaluate effects due to the existence of realistic underdense plasmas. Plasma density increases up to 100 ncr within 25 μm in the linear profile using the same fitting technique, and a 20-μm long plasma of 100 ncr with 200 electrons per mesh is employed in the flattop profile.

It is noted that ions are immobile and the profile is not communicated between the codes but is passed with a file at this moment.

3. SIMULATION RESULTS

As a pilot test problem, we have injected the ignition laser with a Gaussian pulse of wavelength λL = 1.06 μm, intensity IL λL2 = 1 × 1020 W/cm2-μm2, and FWHM = 8λL (70 fs).

The spectra of the reflected lasers are shown in Figure 3 for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile. Odd numbers of higher harmonics are generated by coupling between the laser frequency and 2ωL oscillating ponderomotive force in Figure 3d. The parametric instabilities excited by the laser–plasma coupling in the underdense region can produce a spectrum below the laser frequency with the ALE profiles and it is clearly seen in Figure 3a,b. The oscillating ponderomotive force also generates third harmonics due to the steep profile in overdense regions. The ignition laser can penetrate into the overdense plasma due to the relativistic effect, and the anomalously penetrating pulse is reflected at the recession front (Sakagami & Mima, 1996). Thus the reflected laser is Doppler shifted as shown in Figure 3c. Because there is neither a steep profile nor a long underdense region, no odd higher harmonics are found and frequency modes lower than ωL are not remarkable in the spectrum.

Spectrum of the reflected laser for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile, where ωL is the ignition laser frequency.

Electron energy distributions are shown in Figure 4 for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile. More hot electrons are generated in the ALE profiles due to parametric instabilities excited by the laser–plasma interaction in the underdense region. Superhot electron temperatures can be calculated by slopes of electron energy distribution functions, and are estimated to be 5.5 MeV for both ALE profiles, 3 MeV for the linear profile, and 500 KeV for the flattop profile.

Electron energy distributions for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile. Hot electron temperatures are (a) 5.5 MeV, (b) 5.5 MeV, (c) 3 MeV, and (d) 500 KeV.

Both reflected laser spectrum and electron energy distributions are much different in the realistic plasma profile and the conventional one, and it could be essential to introduce realistic plasma profiles for assessing fast ignition physics by PIC simulations.

4. SUMMARY

We have just started the Fast Ignition Integrated Interconnecting code project to simulate the entire extent of fast ignition, including four different individual codes, namely the ALE hydro code, the collective PIC code, a hybrid code and the Fokker–Planck code. These codes exchange appropriate physical quantities with each other during execution using the lightweight communication protocol, and will be integrated into one big system.

In a first stage of this project, the collective PIC code obtains density profile at maximum compression from the ALE hydro code and introduces imploded plasma, which corresponds to that density profile, into the PIC system. Then an ultrahigh intense ignition laser is launched into the plasma, and we can simulate laser–plasma interaction in a very realistic situation with the PIC code.

We have evaluated reflected laser spectrum and electron energy distributions and found many differences between the realistic plasma profile and the conventional one in PIC simulations. Thus we must introduce the realistic plasma profile into the PIC system to precisely simulate fast ignition physics by the PIC code.

References

REFERENCES

Bell, A.R., Davies, J.R. & Guérin, S.M. (1998). Magnetic field in short-pulse high-intensity laser-solid experiments. Phys. Rev. E 58, 2471–2473.Google Scholar
Honda, M., Meyer-ter-Vehn, J. & Pukhov, A.M. (2000). Two-dimensional particle-in-cell simulation for magnetized transport of ultra-high relativistic currents in plasma. Phys. Plasmas 7, 1302–1308.CrossRefGoogle Scholar
Johzaki, T., Nakao, Y., Kuroki, Y. & Oda, A. (2001). Alpha-particle diffusion code for multi-dimensional ICF simulations. Proc. 2nd Int. Conf. on Inertial Fusion Sciences and Applications, Kyoto, Japan, pp. 236–239. Paris: Elsevier.
Nagatomo, H., Ohnishi, N., Mima, K., Sawada, K., Nishihara, K. & Takabe, H. (2001). Analysis of hydrodynamic instabilities in implosion using high-accuracy integrated implosion code. Proc. 2nd Int. Conf. on Inertial Fusion Sciences and Applications, Kyoto, Japan, pp. 140–142. Paris: Elsevier.
Sakagami, H. & Mima, K. (1996). Anomalous penetration mechanisms of very intense laser pulses into overdense plasmas. Phys. Rev. E 54, 1870–1875.Google Scholar
Sakagami, H. & Mima, K. (2001). Fast ignition simulations with collective PIC code. Proc. 2nd Int. Conf. on Inertial Fusion Sciences and Applications, Kyoto, Japan, pp. 380–383. Paris: Elsevier.
Taguchi, T., Antonsen, T.M. Jr., Lie, C.S. & Mima, K. (2001). Structure formation and tearing of an MeV cylindrical electron beam in a laser-produced plasma. Phys. Rev. Lett. 86, 5055–5058.CrossRefGoogle Scholar
Figure 0

The concept of the Fast Ignition Integrated Interconnecting code (FI3) project. a: A typical density profile in the fast ignition scheme. Each code has responsibility for the indicated areas. b: The code integration diagram. Specified physical quantities should be communicated between codes.

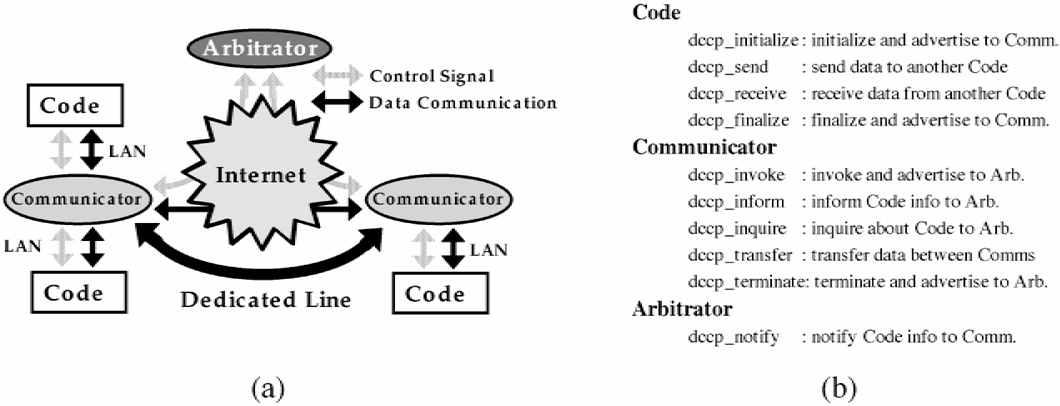
Figure 1

Distributed Computing Collaboration Protocol. Communication chart (a) and summary of protocol (b).

Figure 2

Spectrum of the reflected laser for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile, where ωL is the ignition laser frequency.

Figure 3

Electron energy distributions for (a) the ALE profile cut at 0.1 ncr, (b) the ALE profile cut at 0.05 ncr, (c) the linear profile, and (d) the flattop profile. Hot electron temperatures are (a) 5.5 MeV, (b) 5.5 MeV, (c) 3 MeV, and (d) 500 KeV.