2. SIMULATION CONDITIONS

We choose a simulation box sized X _L × Y _L = 50 λ₀ × 80 λ₀, simulation duration of 250 τ, and grid size of ΔX = ΔY = 0.02 λ₀ and time step of Δt = 0.01 τ, where τ = λ₀/c ≈ 3.536 fs and λ₀ = 1.06 μm are laser period and wavelength, respectively. A p-polarized laser pulse with Gaussian profile in the transverse direction and focal spot of 3.5 λ₀ (full-width half maximum (FWHM)) is introduced along the laser-axis from the left. In longitudinal direction, the pulse shape is assumed to increase to peak intensity in 5 τ, then remain constant for 30 τ before dropping to zero in another 5 τ. The dimensionless amplitude is assumed to be a ₀ = 10.0, where a ₀ is the normalized field amplitude. The electron and ion initial temperatures are both 1.0 keV. We use a double-layer target model (Reference 37) in the simulations. A high-Z (Zme/mi = 1/3672) thin foil target of 1.0 λ₀ thickness and 10.0 λ₀ wide is used as shown in Figure 1. A hydrogen layer (me/mp = 1/1836) is attached to the rear of the high-Z foil target. The density of the high-Z foil is 50n _c, where n _c ≈ 1.0 × 10²¹/cm ³ is the critical density. The density of the hydrogen layer is n _c . The number of particles per cell is 225 electrons and 25 ions for the high-Z foil target, 225 electrons and 225 protons for the hydrogen layer. In order to improve the computational precision, a second-order interpolation algorithm for charge conservation of PIC method (Yu et al., Reference Yu, Jin, Zhou, Li and Gu2013) has been adopted in the code. The boundary conditions of fields are absorption in transverse direction and periodic in longitudinal direction, while the conditions of particles are absorption and reemission. The parameters used in this paper may be not justified; especially the optimal target condition is not addressed here, as this paper's focus is on the TNSA physics.

Fig. 1. (Color online) A laser pulse is irradiated on a high-Z foil target from the left. The thickness, width and density of the foil target are 1.0 λ₀, 10.0 λ₀ and 50n _c, respectively. A hydrogen layer is attached to the rear of the high-Z foil. The density of the hydrogen layer is 1.0n _c

3. EFFECT OF PROTON LAYER WIDTH

In this section, we discuss the simulation results where the transverse width of the proton layer width from 0.1 λ₀ to 10 λ₀, while keeping the thickness fixed to 0.1 λ₀. In the work of Fuchs et al. (Reference Fuchs, Antici, D'Humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pepin and Audebert2006), it is shown that the effective acceleration time is proportional to laser pulse duration, as t _acc ≈ 1.3t _Laser, where t _acc is the effective acceleration time and t _Laser is laser pulse duration. In our simulations, the effective acceleration time should be about 50 τ (our laser duration full-width half maximum is t _Laser ≈ 35 τ), which means that the acceleration process in sheath field is finished at the end of simulation time (250 τ). The proton energy spectra generated from proton layers of different width at t = 250 τ is shown in Figure 2a, the spectra shape is significantly affected by the width of the proton layer. In these results, the average proton energy decreases as the transverse width increases, because protons far from the laser axis acquire a lower energy as shown in Figure 3. The proton cut-off energy however increases as the width grows from 0.1 λ₀ to 6.0 λ₀, and then slightly decreases as shown in Figure 2a. The reason for such a trend is that the proton cut-off energy is affected by both sheath field value and the internal Coulomb explosion of the proton beams, which is investigated in detail below. The proton energy spectrum of a 10 λ₀ wide layer is shown at different times in Figure 2b. One can see that the proton energy spectrum has a sharp peak at early time, expands with time in spite of the fact that we expect the sheath acceleration to have finished, which is due to the Coulomb explosion effect as mentioned above.

Fig. 2. (Color online) (a) Proton energy spectra for different proton layer width (transverse size) at t = 250 τ, from which time the effect of sheath field acceleration is finished for the width of proton layer from 0.1 λ₀ to 10 λ₀ and constant the thickness 0.1 λ₀, (b) Proton energy spectrum of proton layer with 10 λ₀ wide at different times. We can see the expansion of the bandwidth of the energy spectrum after the acceleration process.

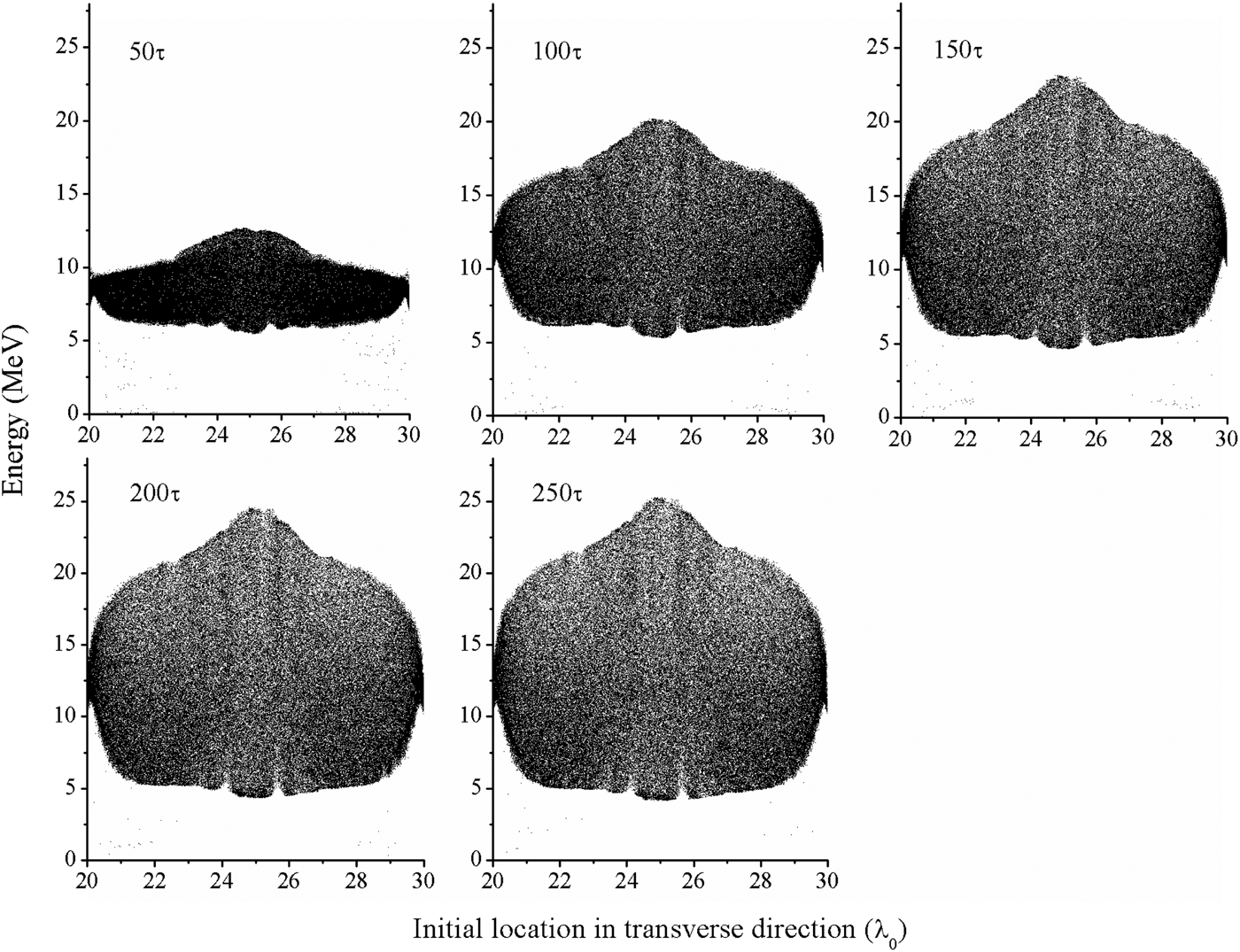
Fig. 3. Relations between proton energy and their initial locations in transverse direction at different times for a proton layer 10 λ₀ wide and 0.2 λ₀ thick.

Figure 3 shows the relation between proton energies and their initial locations in transverse direction at different times. This figure gives two pieces of information. The first one is that the proton energy range varies significantly after the acceleration. This result (and also the result shown in Fig. 2b) indicates that Coulomb explosion plays a very important role in expansion of proton energy spectrum. The second one is that protons with higher energy are originally located near the laser axis. The reason is that E _x, the sheath electric field on the rear of the foil target is stronger near laser axis, because the laser field is strongest there, and thus generates a relativistic electron beam that of high energy on laser axis. Furthermore, the energies of all protons are above 5MeV can be seen from the picture. That is because in this work, we adopt a double-layer target (Esirkepov et al., Reference Esirkepov, Bulanov, Nishihara, Tajima, Pegoraro, Khoroshkov, Mima, Daido, Kato, Kitagawa, Nagai and Sakabe2002) with different ratio of Zme/mi, and the proton layer with a larger ratio than high-Z layer can obtain more efficiency acceleration.

In proton acceleration, proton cut-off energy, proton energy spread, and divergence angle are important parameters to judge the quality of proton beams. From the spectra shown in Figure 2a, we obtain the proton cut-off energy (black curve with squares) and energy spreads (blue curve with squares) for different width of the proton layer as shown in Figure 4a. In order to explain the trends of proton cut-off energy, energy spread, and expansion of energy spectra, we introduce a proton beam Coulomb explosion model during acceleration. The Coulomb explosion should be considered in all directions. For convenience, we divide the Coulomb explosion process into transverse and longitudinal directions, respectively. In the transverse direction, the Coulomb explosion can be assumed to be symmetric around the laser axis, because the sheath field in the transverse direction can be considered to be symmetric along the laser axis. We also assume that all of the electrons escape from the proton layer. Based on these two assumptions, the maximum electric field located at the top or bottom sides of the proton beam can be expressed as

(1)$$\vec E_{in} \left({\displaystyle{w \over 2}\comma \; t} \right)=\vec E_{SW}+2{\rm \pi} en_0 w \cdot \vec n\comma \;$$

where $\vec E_{SW}$ is the sheath field (in longitudinal direction) experienced on proton, which depends on the top (bottom) protons locations, $2{\rm \pi} en_0 w \!\cdot\! \vec n$ (Fourkal et al., Reference Fourkal, Velchew and Ma2005; Zhang et al., Reference Zhang, Shen, Zhang, Wang and Ji2009) is the transverse field experienced on proton from Coulomb explosion effect, where w denotes the width of proton layer, and n ₀ is proton layer's density. $\vec n$ is a unit vector in transverse direction. From Eq. (1), one can see that the maximum electric field due to the Coulomb explosion of the proton beam is proportional to the width and density of the proton layer. In the case of w = 0.1 λ₀ (i.e., the number of protons is very small), the Coulomb explosion effect of the protons is weak and the acceleration can be considered to be dominated by the sheath field. Increasing the width of the proton layer from 0.1 λ₀ to 6.0 λ₀ (the proton number increases), the Coulomb explosion effect on the top (bottom) protons increases significantly, while the effect of sheath field near the laser axis can be considered to be constant because the size of proton layer is fixed in the longitudinal direction. This is why the proton cut-off energy increases with the proton width as shown in Figure 4a (black curve with squares). For Further increase, the transverse size (from 6.0 λ₀ to 8.0 λ₀), although the Coulomb explosion effect on the top (bottom) protons increases, the sheath field experience on these proton become very weak (the sheath electric field on the rear of the foil target is stronger near laser axis as discussed above). For this reason, the proton cut-off energy reduces slightly with further increase of the width as shown in Figure 4a (black curve with squares). This along with the reduced Coulomb explosion means that the energy spread becomes narrower with reduced proton layer width as shown in Figure 4a (blue curve with squares). The trend of energy spread is accordance the experiment results obtained by using small sized proton layer (Pfotenhauer et al., Reference Pfotenhauer, Jäckel, Sachtleben, Polz, Ziegler, Schlenvoigt, Amthor, Kaluza, Ledingham, Sauerbrey, Gibbon, Robinson and Schwoerer2008).

Fig. 4. (Color online) (a) Proton energy spread (blue curve with squares) and proton cut-off energy (black curve with squares) for different proton layer transverse width (the thickness is fixed to 0.1 λ₀) at the time of 250 τ. (b) Proton divergence angles from different proton layer width at the time of 250 τ.

Figure 4b shows the proton beam divergence angle at t = 250 τ again as a function of proton layer transverse width. The proton divergence angle reaches a peak value near 4.0 λ₀ (this value is also influenced by the high-Z layer, proton layer parameters and laser conditions, which will be investigated in the future). To investigate the trend of proton divergence angle shown in Figure 4b, we investigate the relation between proton emergence angle and the initial locations for different proton layer widths as shown in Figure 5. The emergence angle is θ = arctan(v _y/v _x), where v _y and v _x are proton velocities in transverse and longitudinal directions, respectively. From the figure, one can see the following. First, the emergence angle of a proton depends on its initial transverse location. Protons with large emergence angle come from locations far away from the laser axis. (further reasons for this trend can be considered to be proton emergence angle related to proton energy, which is discussed below). The outermost (in transverse direction) protons receive the largest emergence angles. Second, the peak emergence angle increases with the proton layer width because Coulomb explosion effect increases with the width. Meanwhile, the outermost protons compress the inner ones and this compressing force also increases with proton width, therefore, the largest emergence angle does not increase linearly with proton layer width and the divergence angle decreases when the proton width changes from 4.0 λ₀ to 10.0 λ₀ as shown in Figure 4b.

Fig. 5. (Color online) The relation between proton emergence angle and their initial locations at t = 250 τ for an initial proton layer transverse widths of 1.0 λ₀, 4.0 λ₀, 8.0 λ₀.

4. EFFECT OF PROTON LAYER THICKNESS

In this section, we discuss results for different proton layer thickness from 0.04 λ₀ to 1.0 λ₀, while the transverse width is fixed at 5.0 λ₀. The proton energy spectra at t = 250 τ are shown in Figure 6. One can see that the average proton energy decreases with increasing thickness due to the much larger layer thickness. Meanwhile, the maximum and minimum proton energies are affected by the thickness significantly.

Fig. 6. (Color online) Proton energy spectra for different proton layer thickness at the time of 250 τ, the thickness is changed from 0.04 λ₀ to 1.0 λ₀ and the transverse width is fixed to 5.0 λ₀.

From the spectra in Figure 6, we obtain the cut-off energy and the energy spread for different proton layer thickness in Figure 7a. In considering proton energy spread (blue curve with squares), one can see that there is an optimal thickness for proton acceleration. This optimal thickness may be influenced by the laser condition, initial density of proton layer, and foil target. This result also indicates that optimization of the proton layer thickness provides an effective way to obtain high quality proton beams of narrow energy spread. In order to explain the trend of proton cut-off energy shown in Figure 7a (black curve with squares), we introduce a longitudinal (direction of laser incidence) proton beam Coulomb explosion model. We introduce a moving reference frame for the proton beam, in which the Coulomb explosion can be assumed to be quasi-symmetric. The velocity of the moving reference frame varies with time, which is determined by the sheath field. The maximum electric field in the longitudinal direction located at the front of the proton beam can be expressed by an equation similar to Eq. (1)

(2)$$E_{in} \left({\displaystyle{l \over 2}\comma \; t} \right)=E_{SL} \pm \displaystyle{{2{\rm \pi} en_0 l} \over {1+{{2{\rm \pi} n_0 e^2 t^2 } / {m_p }}}}\comma \;$$

where E _SL is the sheath field on the laser axis experienced on proton, the other part of right-hand in Eq. (2) is the electric field from Coulomb explosion (Fourkal et al., Reference Fourkal, Velchew and Ma2005; Zhang et al., Reference Zhang, Shen, Zhang, Wang and Ji2009) (this field is in longitudinal direction), l/2 and m _p denote the coordinate of the proton front in the moving reference frame and the proton mass, respectively. From Eq. (2), one can see that the maximum electric field due to the Coulomb explosion is proportional to the thickness and density of the proton layer. From Figure 7a (black curve with squares), one can see that the proton cut-off energy increases with thickness from 0.04 λ ₀ to 0.45 λ₀, and then decreases when the thickness is above 0.45 λ₀. For thickness up to 0.45 λ₀, the energy due to acceleration from sheath field is almost the same, but the effect of Coulomb explosion increases significantly, which means that the proton cut-off energy is enhanced as the thickness is increased. For further increase proton layer thickness from 0.45 λ₀ to 1.0 λ₀, although the Coulomb explosion effect continues to increase, the screening of the sheath field by the proton layer is also enhanced. This is the reason why the cut-off energy reduces for thickness greater than 0.45 λ₀ as shown in Figure 7a (black curve with squares).

Fig. 7. (Color online) (a) Proton energy spread (blue curve with squares) and cut-off energy (black curve with squares) for different proton layer thickness at t = 250 τ, (b) Proton divergence angles from varies proton layer thickness at t = 250 τ, the proton layer transverse width is fixed at 5.0 λ₀.

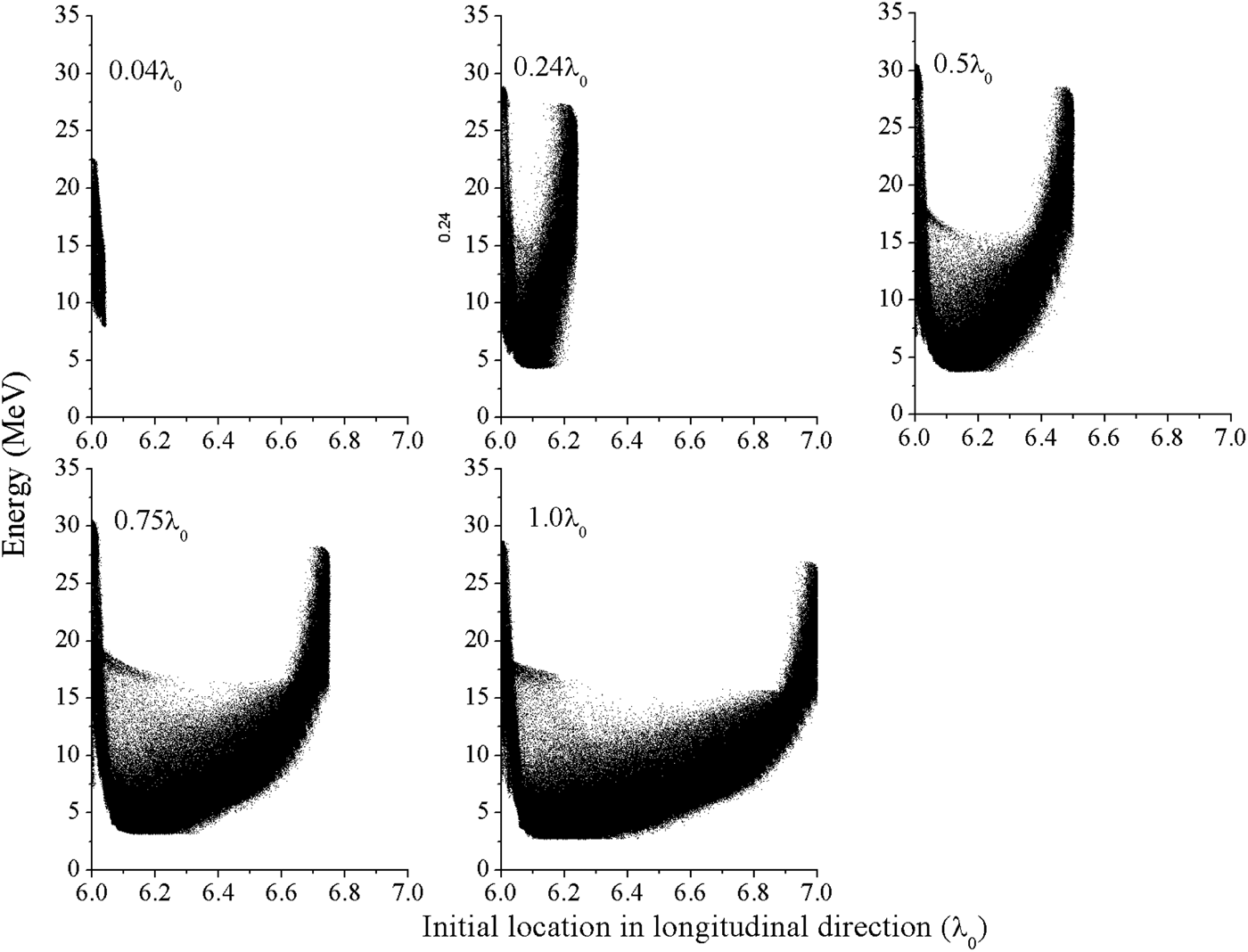
Figure 7b shows the proton divergence angle (full-width half maximum (FWHM)) for different proton layer thickness. From this figure, one can see that the proton divergence angle grows with the thickness. To investigate the mechanism for the proton divergence angle trend shown in Figure 7b, the relation between proton energy and initial longitudinal proton locations is shown in Figure 8. This gives three pieces of information. The first is that the proton cut-off energy and minimum proton energy vary with thickness, determined by both the sheath field and the Coulomb explosion effect. The results are consistent with the spectra shown in figure 6. The second is that the protons with higher energy are initially located at both the front and the rear of proton layer. Higher energy protons are only accelerated from the front of proton layer for ultra-thin proton layer such as for 0.04 λ₀). The third piece of information is that lower energy protons are accelerated from the middle of the proton layer.

Fig. 8. The relation between proton energy and initial locations in the longitudinal direction. The transverse width of the proton layer is fixed to 5.0 λ₀ and the thickness is changed from 0.04 λ₀ to 1.0 λ₀.

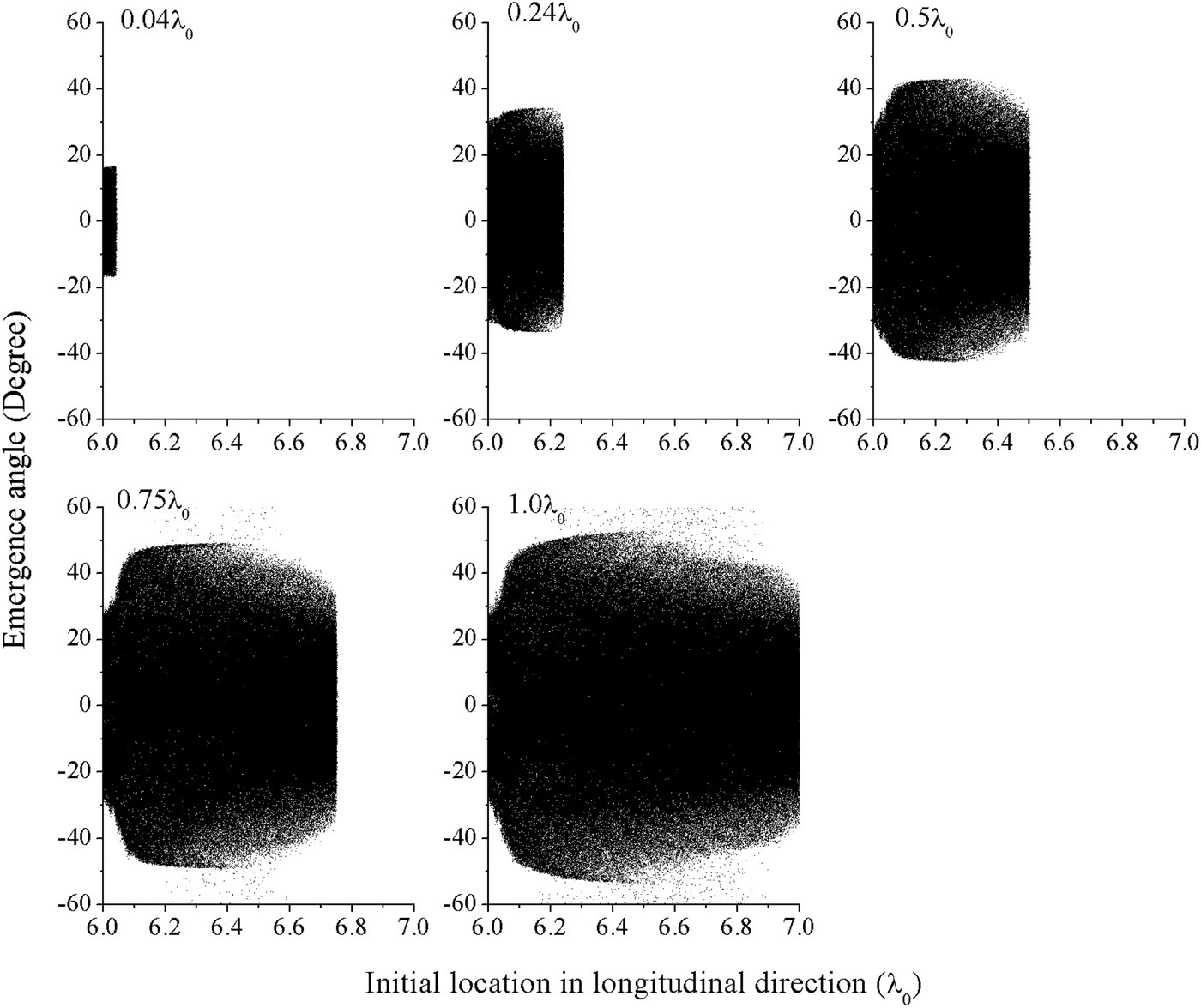
In the work of Andreev et al. (Reference Andreev, Ceccotti, Levy, Platonov and Martin2010), it was found that the proton emergence angle depends on its energy and position, and that protons with higher energy tend to have smaller emergence angle. As we have found in Figures 6 and 8, the minimum proton energy decreases with increasing proton layer thickness. Figure 9 shows protons with larger emergence angle also come from middle of the proton layer, and the largest emergence angle grows with thickness. The results shown in Figures 8 and 9 (also Figs. 3 and 5) are consistent with the results from the model and simulations of Andreev et al. (Reference Andreev, Ceccotti, Levy, Platonov and Martin2010). Meanwhile the results in Figures 8 and 9 also explain why the divergence angle grows with the thickness as shown in Figure 7b.

Fig. 9. The relations between proton emergence angle and initial proton locations in the longitudinal direction. The transverse width of the proton layer is fixed to 5.0 λ₀ and the thickness is changed from 0.04 λ₀ to 1.0 λ₀.