Introduction
Linear induction accelerators (LIA) are widely used as a hard X-ray source with a small spot size. Generation of the X-ray flash is based on the deposition of high current relativistic electron beam on a converter from high Z material (usually the tantalum one). LIA developed recently in the Budker Institute of Nuclear Physics has the energy of electrons of 2 MeV, a beam current of 2 kA, and a X-ray flash duration of 200 ns (Logachev et al., Reference Logachev, Kuznetsov, Korepanov, Akimov, Shiyankov, Pavlov and Fat’kin2013). In the series of special experiments, a satisfactory quality of X-ray images was demonstrated (Starostenko et al., Reference Starostenko, Akimov, Bak, Batazova, Batrakov, Boimelshtein and Kulenko2016). It is well known that a quality of flash X-ray radiography depends on the size of the electron beam spot on the target (Ekdahl, Reference Ekdahl2002). The spot size is affected by several factors such as stability of a focusing system and beam parameters during the pulse. These factors could be controlled well in contrast to the effects associated with the target plasma (Welch and Hughes, Reference Welch and Hughes1998). The state of plasma produced on the target depends strongly on the beam parameters and surface conditions. In the one-pulse operations mode, the plasma affects the beam parameters mainly because of formation of backstream ions. In this paper, we use numerical modeling to study the backstream ion effects in application to the 2 MeV accelerator.
The physical model of beam defocusing was formulated in Welch and Hughes (Reference Welch and Hughes1998). Production of the target plasma leads to the formation of ion emission from the surface. The ions are accelerated by the electric field of electron beam. Space charge of the ions stream disrupts force balance in the electron beam. Thus a self-magnetic field pinches the beam. The focus point of electron beam moves from the target and thus the spot is increased in size. Qualitative estimation of beam defocusing was obtained analytically in a one-dimensional (1D) model (Caporaso and Chen, Reference Caporaso and Chen1998). Characteristic time of beam defocusing was found to be the time for counter-stream ions to pass a part of betatron length of electron beam. In the work of Kwan (Reference Kwan2000), a time that needed for plasma formation was included in beam-defocusing time.
More accurate research was carried out by PIC (particle-in-cell) codes. Well-known MERLIN (Kwan et al., Reference Kwan, Snell and Christenson2000) and LSP codes (Oliver et al., Reference Oliver, Welch and Hughes1999; Vermare et al., Reference Vermare, Davis, Moir and Hughes2003) as well as IPROP (Welch and Hughes, Reference Welch and Hughes1998), M2V (La Fontaine, Reference La Fontaine2007), CONDOR-CODA (Rambo and Brandon, Reference Rambo and Brandon1998) codes were used. Two-dimensional model was considered usually. The numerical modeling allows developing of several ways to mitigate the backstreaming ions effects. However, most of the works consider the dynamics of electron beam with a typical energy of 5 or 20 MeV. The present work is devoted to the beam with an energy of 2 MeV. To compare the results of numerical calculation with the previous works, some typical simulations with 5 and 20 MeV beams are presented.
The fully electromagnetic code KARAT (Tarakanov, Reference Tarakanov1992) based on PIC method was used. The code is capable to simulate non-stationary electrodynamic problem with complicated geometry and including overall types of relativistic particles as ions, neutral, and electrons (see, e.g., Eltchaninov et al., Reference Eltchaninov, Korovin, Rostov, Pegel, Mesyats, Rukin and Ginzburg2003; Xiao et al., Reference Xiao, Zhang, Zhang, Li, Zhang, Song and Liu2010; Mesyats et al., Reference Mesyats, Reutova, Sharypov, Shpak, Shunailov and Yalandin2011; Cai et al., Reference Cai, Liu, Ju, Zhao, Zhou and Wang2016; Dubinov and Tarakanov, Reference Dubinov and Tarakanov2017). To obtain plasma parameters, a complicated self-consisted problem should be solved. Indeed, it was studied in the works of Oliver et al. (Reference Oliver, Welch and Hughes1999); Davis et al. (Reference Davis, Olson and Moir2003); Vermare et al. (Reference Vermare, Davis, Moir and Hughes2003); La Fontaine (Reference La Fontaine2007) in some approximations. The plasma is produced through evaporation of impurity or target material itself. Subsequent ionization could be produced by direct impact of beam electrons. Electric breakdown through the beam electric fields also could work. In spite of the possibility in principle to use KARAT for the calculation of plasma formation at target, we had included ion emission phenomenologically, which would be discussed below.
Basic computational model
For simulation, the geometry of the target cell of LIA was simplified in the next way. A simulation domain is bounded by a conducting cylindrical surface of 40 cm length and 6 cm in diameter. A final focusing lens is a coil that has a rectangular cross-section of winding. In such a manner, the problem was simulated in cylindrical R-Z axial symmetry coordinates. We used a uniform grid with 240 nodes in radial and 1800 nodes in axial direction. Typical cell dimension was of about 0.1 mm. Monoenergetic electron beam was emitted from the left end of conducting cylinder. Initial distribution of current density of the beam has been set uniform. Opposite side of the cylinder corresponds to the target. Main characteristics of the beam were as follows: energy of 2 MeV, beam current of 2 kA, initial beam diameter of 40 mm. Magnetic field of final lens was tuned to maintain a spot size diameter lower than 1 mm at target. The axial length of the modeled region has been made getting into account the Bush theorem (see, e.g., Lawson, Reference Lawson1977). It means that, a non-zero magnetic field of the final lens at the beam starting surface should not prevent the beam compression on the target due to the conservation of transverse momentum. The energy of the beam was set constant in time to avoid a numerical instability. The beam current was approximated as a step function with a rise time of 1 ns. A stable converged beam state was achieved after ~5 ns. After that the ion emission from the target plane was switched on with 2 ns rise time. In most simulations, the value of the ion current was determined by the Child–Langmuir law. It is a worst case for defocusing. We also studied the ion emission with a current about ten times less in the so-called one monolayer case (Oliver et al., Reference Oliver, Welch and Hughes1999) for comparison. The emitted ions had a uniform velocity distribution at azimuthal and polar angle and uniform energy distribution from 1 to 10 eV. In the papers mentioned above, a hypothesis was introduced that the plasma on the target surface is produced from carbon, air, and water, that is, from surface impurities. Thus for typical calculation, we used three types of ions: protons, low ionized carbon (as typical impurity and close to the mass of nitrogen and oxygen), and tantalum by itself.
Results and discussion
Results of calculations
We considered the emission of protons from the target surface as typical and most commonly suggested as a worst case. The current density of the protons was set as a space charge limited one. Figure 1a shows the R-Z particle position plot before the ion emission. The electron beam is injected from the left boundary of the calculation domain with an initial radius of 20 mm. The beam is focused through final magnetic lens on the right boundary (target) with a diameter slightly lower than 1 mm. The emission of ions with a diameter of 2 mm was switched on with 2 ns rise time. Figure 1b, 1c shows the temporal evolution of the electron beam and the ions at moments 5 and 20 ns after beginning the emission.
Fig. 1. Positions of macroparticles on the R-Z plane at several moments: (a) initial stage of beam defocusing, that is, vacuum case; (b) at 5 ns in case of space charge-limited emission of proton emission; (c) at 20 ns in case of space charge-limited emission of proton emission; (d) at 20 ns in case of “low” emission of protons.
At the initial moment (i.e., 5 ns), the ion stream was radially uniform. Further radial distribution of the emission of ions becomes substantially annular. Herewith the electron beam was over-focused, a beam cross-over moved in front of the target, and the beam had an annular radial structure on the target. When the cross-over of the beam moves out, a self-consisted electric field near the surface of the target changes. It decreases on the axis and increases on the edge where the annular beam hit the target. Because of this the backstream of ions becomes annular one. The same structure of the ions backstream was also reproduced with 5 and 20 MeV energies of the electron beam. It seems that an analogical pattern could be seen in PIC modeling presented at the work (Welch and Hughes, Reference Welch and Hughes1998).
Figure 1d shows a snap shot of the beam and the backstream ions at 20 ns, when the ions were emitted with a low current density. As one could see, a ten times lower emission practically does not disturb the beam equilibrium. The beam cross-over had been maintained on the target and the beam spot size had been stayed unchanged.
The stream of ions is confined well near the axis into a electrostatic trap produced by the electron beam space charge. However, the ions oscillate radially. The velocity of the ions is higher in the case of space charge-limited emission, as could be seen in Figure 1c, 1d. The head of the ions stream achieves a velocity of 1 cm/ns. An explanation of this phenomenon was proposed in the work of Stupakov (Reference Stupakov1976) dedicated to bipolar diodes. A space charge of bulk ions beyond the head of the stream leads to an additional acceleration of the head.
There are different criteria of the beam defocusing in the sense of spot size. In the present work, we consider the spot size up to 2 mm as acceptable. In the case of the space charge-limited emission of protons, the electron beam with 2 MeV energy is defocused during several nanoseconds. One could make the estimation of beam-defocusing time by the formula obtained in Kwan (Reference Kwan2000):
$$\eqalign{\tau {\mkern 1mu} =& {\mkern 1mu} \displaystyle{{\pi \cdot r_{\rm b}} \over 4}\cdot \left( {\displaystyle{{I_0} \over {I_{\rm b}}}} \right) \cr & \cdot \left[ {\left( {\displaystyle{{m_{\rm i}} \over {m_{\rm e}}}} \right)\cdot \displaystyle{{\gamma \beta } \over {\bar{Z}c^2\left[ {1-2{\rm ln}(\displaystyle{{r_{\rm b}} \over {r_{\rm w}}})} \right]\cdot \left| {\displaystyle{1 \over {\gamma ^2}}-\eta } \right|}}} \right],} $$where r b is the beam radius, r w is radius of a beam pipe, I 0 is the Alfven current, that is, 17 kA, I b is the beam current in kA, m i and m e are the mass of ions and electrons, 
$\bar{Z}$ is a mean charge of ions, η is the neutralization factor, γ and β are the relativistic factors of the beam. In our case, the estimation gives the value of 3 ns.
A current of the protons has a value of several amperes. This value is lower than the one that could be obtained from the interpolation formula proposed in Welch and Hughes (Reference Welch and Hughes1998):
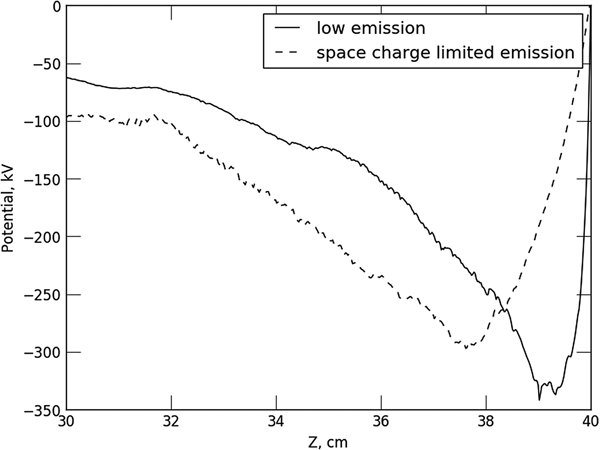
$$Ii({\rm kA})\approx \displaystyle{{17} \over 5}\cdot \lpar {2{\rm \nu}} \rpar ^{\displaystyle{3 \over 2}}\cdot \left[ {\displaystyle{{Z\cdot m_{\rm e}} \over {m_{\rm i}}}} \right]^{\displaystyle{1 \over 2}},$$where Z is an ion charge, m e and m i are the masses of electron and ion, ν is the Budker parameter (Lawson, Reference Lawson1977). This expression is based on the analytic estimation, while the numerical factor was obtained from 2D modeling. Substituting the considered beam parameters in the expression (2) we obtain a current of about 9 A. The difference between this value and the results of our simulations can be explained by a slightly different shape of the beam near the target. Before the emission of the ions starts, a potential gradient scale length near the target is of the order of the beam spot size. Figure 2 shows an on-axis potential distribution. One can see that the ion emission changes the scale length to several centimeters. The electric field strength in vicinity of the target surface is decreased and the ion current density correspondingly reduces.
Fig. 2. Electrostatic potential profile on axe nearby the target for two types of ion emission.
Influence of different factors on the beam spot size
Dynamics of the beam spot size should depend on the plasma and the beam parameters. First of all, we considered the influence of a size of the plasma nearby target. An expansion of the bulk plasma in axial direction during the pulse of accelerator is considered as negligible usually. A diameter of the ion emission region is of the order of the beam spot size. We have considered a few values of the diameter of the emission region between 0.5 and 5 mm. Figure 3a shows the dynamics of the beam spot radius in the cases of different diameters of the emission region. In the case of 1 mm diameter of emission region, the beam is defocused faster than in the case of 0.5 mm diameter. It results from increasing of total injected current of ions in accordance to increasing the emission area. For diameters of ion emission region larger than 2 mm, defocusing occurred slower. It is bound with the effect of transition of ion emission profile from axially sharped distribution (in first nanoseconds of emission establishing) to the annular one in later moments. Though in an emission area with larger diameter, the total injected current increased but simultaneously ions should travel longer distance from the edge of the predefined emission areas. Nevertheless, any reasonably predefined emission area leads to fast destruction of the force balance inside the beam during 2–5 ns. This fact shows that the beam dynamics in the sense of spot size depends on the emission capability of the target plasma. Thus, the final stage of spot degradation is weakly bounded with plasma size and local parameters. We have observed the saturation of the beam mean radius after about 10 ns. It seems to be due to the finite size of the calculation domain.
Fig. 3. Mean beam radius at the target versus time. (a) Proton emission in space charge limit with different size of emission region. (b) Emission of different ion species from target surface.
Figure 3b shows the dynamics of the beam spot in the cases of different ion species emitted from the target. The cases of carbon and tantalum emission are presented. As mentioned above in the case of proton emission and the beam energy of 2 MeV, the defocusing occurs within a few nanoseconds. An ion velocity v i is proportional to 
$\sqrt {{\rm \varphi} /M_{\rm i}} $, where the potential deep near the target is ϕ and M i is the ion mass. Therefore, the defocusing time is proportional to ~
$1/\nu _{\rm i}\sim \sqrt {M_{\rm i}} $. Light impurities such as carbon and nitrogen are almost the same destructive as hydrogen. The defocusing of the beam takes about 10 ns in this case. Low-ionized states of tantalum do not change the beam size during tens of nanoseconds.
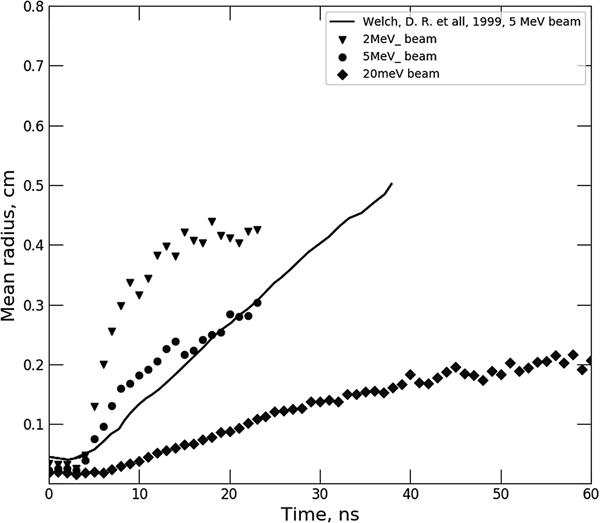
Figure 4 shows the dynamics of the beam spot in the case of 2 kA beam current and three representative beam energies: 2, 5, and 20 MeV. The space charge-limited emission of protons is considered. One could see from Figure 4 that the defocusing time decreases with the beam energy. It results from the fact that a radial acceleration of beam electrons is inversely proportional to the relativistic factor γ for a given transverse force value. Again, the comparison with the result of Oliver et al. (Reference Oliver, Welch and Hughes1999) is presented. Authors of this paper have considered the emission of ionized molecular hydrogen, that is, H2+. The given simulation had a very close geometry of beam, drift channel, and ions emission. Parameters of the focused electron beam were as follows: a beam energy of 5.5 MeV and a beam current of 2 kA. Mostly, our results of calculation are in agreement with the referenced trend of spot behavior during the beam pulse. This fact follows from the above-mentioned dependence between the time travel of ion and the mass, because in both simulations the mass differs only two times.
Fig. 4. Mean beam radius at the target versus time in cases of different energy of the beam. A comparison with results of Oliver et al. (Reference Oliver, Welch and Hughes1999) is shown.
Mitigation of beam defocusing
Let us consider the methods of suppression of the beam defocusing, which arise from the backstream ions in the case of low beam energy of 2 MeV. At first we will discuss the barrier foils proposed before (Chen et al., Reference Chen, McCarrick, Guethlein, Caporaso, Chambers, Falabella and Weir2002). It is believed that the grounded foil in front of the target surface can produce electrostatic gap for the ions emitted from the target. However, in the case of 2 MeV beam, the foil could substantially scatter the electrons. Again, the beam impact could produce a surface plasma on the foil and reproduce a backstream of ions. It was shown, for example, in the experimental work dedicated to the diagnostic foils for optical transition radiation diagnostic (Vermare et al., Reference Vermare, Donohue, Labrouche, de Gabory and Villate1999). Thus we discuss a few non-invasive techniques further.
An attractive way is a formation of potential barrier for backstreamed ions by electrostatic or inductively induced electric field. It was studied in many works (Chen et al., Reference Chen, Houck, McCarrick and Poole1998; Kwan et al., Reference Kwan, Snell and Christenson2000; La Fontaine et al., Reference La Fontaine, Lemaire, Quine and Segré2000, Reference La Fontaine, Guilhem, Lemaire and Quine2002) and approved by numerical modeling and experiments. Nevertheless, this approach substantially complicates a design of a target unit. It requires a high voltage decoupling of target and maintaining a hundreds of kilovolts voltage in the presence of gas and plasma. In Caporaso et al. (Reference Caporaso, Chen and Paul1998), it was proposed to stabilize the spot size by varying the beam energy or magnetic field of the final focusing lens during beam pulse. We have considered this approach for 2 MeV beam. The simulation described above shows that the beam cross-over moves about a 2 cm distance per 10 ns. A focus length of the final lens is about 10 cm, thus one should increase the focus length by 25% over the initial value. The focus length is proportional to the relativistic parameter γ in square and inversely proportional to the magnetic field strength in square. Thus, one should increase the energy of electrons by about 10% to compensate ion defocusing. However, magnetic-focusing elements at the beam transport line are adjusted for a nominal beam energy to conserve low beam emittance. The variation of energy could be a desirable way only if an additional acceleration cell would be constructed between the transport system and the final lens. By these reasons, it seems that the variation of magnetic field of the final lens is more favorable. Figure 5 demonstrates a possibility of suppression of dynamical defocusing of the electron beam in the initial stage. It requires reducing the current in the final solenoid with a rate of 300 Ampere-turns per nanosecond. A pulsed power modulator with tens of nanoseconds rise time should be constructed to achieve it. Moreover, a transient magnetic field cannot penetrate inside a vacuum chamber due to eddy currents. Because of this reason, a low inductance coil should be installed inside the target chamber.
Fig. 5. Mean beam radius at the target versus time. Dynamical compensation of beam defocusing by final lens current variation of 300 A/ns. Squares – compensation on, circles – compensation off.
Conclusions
The simulations show that the 2 MeV beam is very sensitive to ion defocusing. The space charge-limited emission of protons affects the beam after 1–2 ns. A few tens of nanoseconds are enough even for low-ionized states of tantalum to completely disrupt the electron beam. Thus a proper preparation of the target surface is essential to achieve a small spot size of the beam. The possibility of emission of tantalum ions depends on power deposition inside the target. Thus the beam pulse should be as short as possible and some variation in target geometry or beam spot size would be possible to decrease the deposition. Alternatively, the influence of ions is negligible for 20 MeV beam with a duration lower than 100 ns in case of no impurities on the target surface. Again, in this case, even the emission of the protons does not disrupt the beam during 40 ns. A several non-invasive techniques of mitigation of the beam disruption were considered. It seems that a controlled variation of magnetic field of the final lens is a more desirable way. It requires reducing the current in the final lens with a rate of 300 Ampere-turns per nanosecond during the pulse to mitigate the influence of proton emission. This approach could be used only in case of good repeatability of the beam parameters. Furthermore, a process of the plasma formation should be reproducible during each beam pulse.
Acknowledgments
This work was supported by the Russian President grant (project SP-3900.2016.2).
