Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T15:21:58.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamics of plasma and shock waves generated by the high-power GARPUN KrF laser

Published online by Cambridge University Press:  01 March 2004

V.D. ZVORYKIN ,
V.G. BAKAEV ,
I.G. LEBO  and
G.V. SYCHUGOV
V.D. ZVORYKIN
Affiliation:
P.N. Lebedev Physical Institute, Russian Academy of Sciences, Moscow, Russia
V.G. BAKAEV
Affiliation:
P.N. Lebedev Physical Institute, Russian Academy of Sciences, Moscow, Russia
I.G. LEBO
Affiliation:
Moscow Institute of Radioengineering, Electronics and Automation (Technical University), Moscow, Russia
G.V. SYCHUGOV
Affiliation:
P.N. Lebedev Physical Institute, Russian Academy of Sciences, Moscow, Russia
Rights & Permissions [Opens in a new window]

Abstract

The electron-beam-pumped KrF laser installation GARPUN with a 100-J output energy and long 100-ns pulse duration has been used to investigate laser–target interactions in a broad range of laser intensities for small (150 μm) and large (∼1 cm) irradiated spots. For higher intensities (up to 5 × 1012 W/cm2), a conical shock wave was generated in condensed matter by megabar pressure at the ablation front. It propagated with a supersonic velocity in a quasisteady manner together with a conical shock wave inside a target. Evaporated target material moving with a velocity of ∼50 km/s formed an extended plasma corona of ∼5 mm length with an electron temperature of ∼100 eV. Emission spectra of plasma have been investigated in the extreme UV range 120–250 Å. For lower intensities (108–109 W/cm2), planar shock waves in normal density air were produced with initial velocities up to 4 km/s in the forward direction and 7 km/s in the opposite direction toward incident radiation. In rarefied air, the forward shock wave kept velocities constant whereas the backward ones were accelerated up to 30 km/s. Planar compression waves in transparent condensed matter were also demonstrated propagating with sonic velocity.

Keywords

High-power KrF laser–target interactionPlanar and conical shock waves in condensed matterPlanar hypersonic shock waves in gases
Type
International Conference on the Frontiers of Plasma Physics and Technology
Information
Laser and Particle Beams , Volume 22 , Issue 1 , March 2004 , pp. 51 - 57
Copyright
2004 Cambridge University Press

1. INTRODUCTION

A number of powerful KrF lasers with electron-beam pumping and output energies up to several kilojoules have been developed, and target shooting experiments were performed through the last two decades at AURORA (Harris et al., 1993; Sullivan et al., 1993), NIKE (Obenschain et al., 1996; Pawley et al., 1997; Mostovich et al., 2000; Weaver et al., 2001; Aglitskiy et al., 2002), SPRITE (Shaw et al., 1993; Divall et al., 1996), and ASHURA (Owadano et al., 1993, 1996; Kadano et al., 2000). These experiments, aimed at clarifying the status of KrF drivers for inertial confinement fusion (ICF), were carried out in an intensity range of 1011–1014 W/cm2 and a pulse duration of a few nanoseconds. Plasma parameters, X-ray emission, equation of state of compressed matter, acceleration of planar foils, and hydrodynamic instabilities growth have been studied.

In contrast to them, in our experiments at the GARPUN KrF installation (Basov et al., 1993) plasma and shock waves (SW) were generated by laser pulses of 100-J energy and a long duration of 100 ns. When being focused sharply by a F = 400 mm spherical mirror into a focal spot of 150 μm diameter, peak intensity as high as 5 × 1012 W/cm2 has been reached. The salient features of such a long-pulse laser–target interaction were high penetration rate of radiation throughout the matter and conical SW formation (Zvorykin & Lebo, 1999; Zvorykin et al., 2000). In another performance with a prism raster focusing a uniform large-spot target, irradiation by moderate intensities in the range of 108–109 W/cm2 has been investigated to verify a concept of a laser-driven shock tube (LST) proposed by Zvorykin and Lebo (2000). This novel laboratory technique to generate hypersonic SW in gases and compression waves in liquids might be applied for studies of hydrodynamic instabilities at contact interfaces between different liquids and gases, hypersonic gas flow around the bodies, effects of strong SW refraction, and cumulation in a time scale of several microseconds and a space scale of 10 mm. This article describes briefly the main results of both investigations.

2. HIGH-INTENSITY LONG-PULSE LASER–TARGET INTERACTION

Extended craters of about 1 mm depth were produced in all solid targets under investigation (Li, C, CF4, Plexiglas, Mg, Ca, Ti, Fe, Zn, Ge, Ta, W, Pb) during laser action. Cone-shaped SW was evidently seen in Plexiglas (Fig. 1) being generated by megabar-range pressure (Zvorykin & Lebo, 1999; Zvorykin et al., 2000) at an ablation front propagated inside the matter. It was quite similar to the well-known Mach cone in a gas created by a body moving with a supersonic velocity. Using the relation for the Mach angle: sin αM = c/Vab, where αM = 30–40° is a half angle at the cone vertex and c = 2.7 km/s is the sound velocity in Plexiglas, one could estimate an ablation front velocity Vab = 4–5 km/s. For lower laser intensities a semispherical SW was observed, thus revealing that ablation front velocity became subsonic. Side-lobe perturbations on the crater surface evidenced strong tangential moving between compressed layers, giving rise to Kelvin–Helmholtz instabilities.

Micropicture of a conical SW and crater produced in Plexiglas obtained in a projection scheme with the polarized light of a copper-vapor laser.

By using streak camera records for thin Al and graphite targets, SW transit time and burn-through time tb were measured for different laser intensities q and target thicknesses d. The former was detected as a relatively weak luminescence appearing at the backside; the latter was accompanied by material ejection and penetration of laser light to a screen placed behind. These experiments and also two-dimensional numerical simulations have proven that a conical SW propagated in a self-regulated manner together with the ablation front. Laser pulses of 100 ns penetrated through target thicknesses as large as 330 μm. An average velocity of the ablation front Vab = d/tb during the first 50 ns was about 5 km/s. The maximum value corresponding to the 20–50 ns interval was ∼8 km/s. Effective mass ablation rates determined as

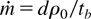
were derived, where ρ0 is an initial density of the target material. They are presented in Figure 2 in comparison with previous mass ablation measurements for nanosecond pulses and different laser wavelengths. Being described by the formula

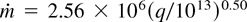
, where q is expressed in W/cm2, they exceed by an order of magnitude mass ablation rates for short pulses. There might be several explanations for the discrepancy. First, long-pulse laser radiation could be self-focused in the extended plasma corona (Fig. 3). To achieve the measured values of

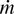
the intensities of ∼1015 W/cm2 are necessary. High temperature and corresponding highly ionized ions should be detected in the plasma corona in that case.

Dependence of mass ablation rate on laser intensity compared for different experiments: 1: present work; 2,3,4: obtained by Ng et al. (1984); 5,6: obtained by Dahmani and Kerdjia (1991); 7,8,9: obtained by Key et al. (1983).

Pin-hole image of aluminum plasma in the soft X-ray range (left) and spatially resolved images of plasmas from different materials in the extreme UV range (right).

As has been measured by a streak camera in a visible spectral range, the plasma stream went away from the irradiated surface toward the incident laser radiation with a velocity of ∼50 km/s. A time-integrated pin-hole plasma image obtained in a soft X-ray region λ < 12 Å by transmitting radiation through beryllium foil is shown in the left of Figure 3. Electron temperatures of the plasma corona being measured with an error ±10 eV for various target materials by X-ray absorption in beryllium foils of different thicknesses are listed in Table 1. These values of Te = 100–135 eV are typical for the intensity range of ∼1012 W/cm2.

Electron temperature of plasmas measured by X-ray absorption in beryllium foils

We have also investigated emission spectra of plasma for different target materials in the extreme UV range 120–250 Å by means of a compact spectrograph based on MoSi2-Si sliced multilayer grating (Levashov et al., 1994). They are shown in the right of Figure 3 and their identifications are presented in Figure 4. The highest ionization potential for CVI ions observed in the spectra was 490 eV. No additional spectral lines belonging to highly ionized ions were observed if compared with the emission spectra of plasma heated by a Nd:YAG laser with approximately the same intensity (Levashov et al., 1994). Thus we confirmed that, notwithstanding a large plasma extension of ∼5 mm, there was no self-focusing of laser radiation.

Emission spectra of plasmas in the extreme UV range from different target materials.

Indeed, as has been demonstrated earlier (Zvorykin & Lebo, 1999), fast penetration of laser radiation throughout the matter in our experimental conditions of the essentially two-dimensional character of the hydrodynamic flow when a conical shock wave propagated along a distance exceeding the diameter of the irradiated spot could be explained by radial squeezing out of the matter. It contributed, mainly, to hole burning of a target in contrast to one-dimensional conditions for nanosecond laser pulses, where a burn-through process was determined by a mass flow of target material through an ablation front.

3. MODERATE-INTENSITY LASER–TARGET INTERACTION

In the proposed design of the miniature LST, hypersonic SW would be excited in a contained gas due to acceleration of thin foils along a channel of ∼1 × 1-cm2 cross section by means of a high-power KrF laser. When radiation is absorbed by a thin opaque foil adjacent to a rear surface of an input window, pressure arising in such a plasma-confinement geometry may reach ∼10 kbar at relatively low laser intensities q ≤ 109 W/cm2 (Zvorykin & Lebo, 2000). It would accelerate the remaining part of the foil and push a strong SW in a gas, lateral expansion being restricted by sidewalls of the tube. In another performance, LST could be filled by immiscible liquids or liquid and a gas to investigate development of hydrodynamic instabilities at contact interfaces between different matters under pulsed acceleration during a pass of a compression wave. There are many organic liquids that strongly absorb UV radiation and, therefore, they are suitable to generate compression waves due to laser energy release just behind the window.

Initial experiments have been performed with various solids and CH films of 1 to 10 μm thickness. To prevent initial perturbations, we have used a focusing system that combined a multielement prism raster (Fig. 5) and a lens. By splitting an incident laser beam with a cross section of 10 × 10 cm into 25 individual 2 × 2 cm beamlets and overlapping them at a focal plane, this system provided nonuniformity less than a few percent across the square spot. The spot size could be changed from 20 × 20 to several millimeters by moving the lens. Corresponding laser intensities were varied in the range q = 108–109 GW/cm2.

Principle of prism raster (left) and laser radiation patterns before the focal plane and at the focal plane (right).

Figure 6 demonstrates slit-scanning images of laser–target interactions obtained by a high-speed optomechanical camera in combination with the Schlieren method using a quasisteady capillary-discharge light source. The targets were set inside a chamber with variable air pressure p0 = 0.0002–1 bar. During laser pulse action, the plasma front coincided with the SW front and they expanded together from the target surface toward the incident radiation with a velocity independent of the target material. This looks like a laser-supported detonation wave (LSDW), whose velocity is expressed by Raizer's (1965) formula:

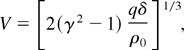
where γ = 1.2 is a specific heat ratio for air plasma, ρ0 = 1.29 × 10−3 g/cm3 is normal air density, and δ is absorption of radiation. Dependences of SW and plasma front velocities on laser intensity and air pressure are shown in Figures 7 and 8 for an iron target. Solid lines in Figure 7 correspond to calculated velocities of LSDW with different absorption δ. It is seen that only a small part of the incident radiation δ = 0.1 (line 2) was absorbed and it is unlikely the detonation mechanism could support the SW velocity. Most of the laser radiation penetrated through the SW and caused target evaporation. Expanding vapors maintained SW velocity in the surrounding air. Being calculated in numerical simulations (dashed lines) with allowance for vapor ionization (line 3), they were in agreement with measurements. Close values of the SW velocity were calculated also for an aluminum target that coincided with experiments. At low air pressures p0 < 0.1 bar (Fig. 8), the SW velocity did not depend on air pressure at all increasing up to 30 km/c.

Slit-scanning images of laser interaction with solid (a), transparent (b), and foil targets (c).

Velocities of the plasma front and SW depending on laser intensity for atmospheric air. Solid lines: calculations for LSDW with δ = 1 (1) and δ = 0.1 (2); dashed lines: numerical simulations with allowance for the ionization process (3) and fixed ion charge Z = 3 (4).

Velocity of the plasma front and SW depending on air pressure for laser intensities 0.3–0.6 GW/cm2.

Temporal evolution of the SW generated in the normal density air in front of the target after termination of a laser pulse is shown in Figure 9. Similar x-t diagrams were obtained also for a rarefied air. The SW damping law independently on laser intensity and air pressure could be approximated by a power law x ∼ tn with power indexes n1 = 0.85–0.95 at the initial stage and n2 = 0.5–0.6 later, when the distance of the SW front from a target became comparable with the size of the irradiated spot. These are different from n1 = 0.67 and n2 = 0.4 observed for a SW in similar experiments by Danilychev and Zvorykin (1984) with a powerful pulsed CO2 laser. The latter indexes corresponded well to the model of a strong mass-free explosion (Sedov, 1959) because of high absorption of IR laser radiation in the shocked air. Present results confirm that a SW generated by a UV laser in the ambient gas was due to target evaporation.

x-t diagrams for SW in atmospheric air at various laser intensities 0.2–0.8 GW/cm2.

Figure 6b demonstrates interaction of a laser pulse with a glass. KrF laser radiation was fully absorbed by this material and caused its evaporation, whereas it was transparent for a visible probe light. A compression wave was generated at the surface by ablation pressure and propagated inside the sample with a sound velocity. Thin CH targets of 3–5 μm thickness have been accelerated up to velocities ∼4 km/s (Fig. 6c). Acting as a pusher they produced planar shock waves in a gas behind the irradiated foil target. Increasing of the air densities did not essentially influence the initial velocities of the backside of the SW but increased their decay.

4. CONCLUSIONS

Plasma flows and shock waves generated by 100-J, 100-ns laser pulses have been investigated at the GARPUN KrF installation in a broad intensity range for small (∼150 μm) and large (∼1 cm) irradiated spots. In the high-intensity (up to 5 × 1012 W/cm2) region, megabar ablation pressures were generated and produced in essentially two-dimensional geometry a cone-shaped SW. It propagated in a self-regulated manner together with the ablation front, resulting in a very high penetration rate of laser radiation due to radial squeezing out of the solid matter. In the moderate-intensity (108–109 W/cm2) region, experiments have been performed to verify the LST concept. Planar shock waves with velocities up to 7 km/s toward the laser beam have been observed in normal density air and up to 30 km/s in rarefied air. Acceleration of thin foils has been demonstrated up to a velocity of 4 km/s and they produced SW in the forward direction.

ACKNOWLEDGMENTS

This work was supported by the Russian Foundation for Basic Research, Project No. 01-01-00023 and Independent International Association formed by the European Community (INTAS), Project No. 01-0846.

References

REFERENCES

Aglitskiy, Y., Karasik, M., Serlin, V., Pawley, C.J., Schmitt, A.J., Obenschain, S.P., Mostovych, A.N., Gardner, J.H. & Metzler, N. (2002). Direct observation of mass oscillations due to ablative Richtmyer-Meshkov instability and feedout in planar plastic targets. Phys. Plasmas 9, 2264–2276.CrossRefGoogle Scholar
Basov, N.G., Bakaev, V.G., Bogdanovskii, A.V., Vadkovskii, A.D., Grigor'yants, E.A., Zvorykin, V.D., Metreveli, G.E., Suchkov, A.F. & Sychugov, G.V. (1993). E-beam pumped “GARPUN” broadband KrF laser with ∼1GW pulsed lasing power. J. Sov. Laser Res. 14, 326–359.CrossRefGoogle Scholar
Dahmani, F. & Kerdjia, T. (1991). Measurements and laser-wavelength Dependence of mass-ablation rate and ablation pressure in planar Layered targets. Laser & Particle Beams 9, 769–778.CrossRefGoogle Scholar
Danilychev, V.A. & Zvorykin, V.D. (1984). Experimental investigation of radiation-gasdynamic processes that develop under the action of high-power λ=10.6 μm laser pulses on a solid in a gas. J. Sov. Laser Res. 5, 667–715.Google Scholar
Divall, E.J., Edwards, C.B., Hirst, G.J., Hooker, C.J., Kidd, A.K., Lister, J.M.D., Mathumo, R., Ross, I.N., Shaw, M.J., Toner, W.T., Visser, A.P. & Wyborn, B.E. (1996). Titania—a 1020 Wcm−2 ultraviolet laser. J. Mod. Opt. 43, 1025–1033.Google Scholar
Harris, D.B., Allen, G.R., Berggren, R.R., Cartwright, D.C., Czuchlewski, S.J., Figueira, J.F., Hanson, D.E., Hauer, A., Jones, J.E., Kurnit, N.A., Leland, W.T., Mack, J.M., McDonald, T.E., McLeod, J., Rose, E.A., Sorem, M., Sullivan, J.A. & Watt, R.G. (1993). Strength and weakness of KrF lasers for inertial confinement fusion applications learned from the AURORA laser. Laser and Particle Beams 11, 323–329.CrossRefGoogle Scholar
Kadano, T., Yoshida, M., Takahashi, E., Matsushima, I., Owadano, Y., Ozaki, N., Fujita, K., Nakano, M., Tanaka, K.A., Takenaka, H. & Kondo, K. (2000). Reflected shock experiments on the equation-of-state properties of liquid deuterium at 100–600 Gpa (1–6 Mbar). Phys. Rev. Lett. 45, 1046–1048.Google Scholar
Key, M.H., Toner, W.T., Goldsack, T.J., Kilkenny, J.D., Veats, S.A., Cunningham, P.F. & Lewis, C.L.C. (1983). A study of ablation by laser irradiation of plane targets at wavelengths 1.05, 0.53, and 0.35 μm. Phys. Fluids 26, 2011–2026.Google Scholar
Levashov, V.E., Zubarev, E.N., Fedorenko, A.I., Kondratenko, V.V., Poltseva, O.V., Yulin, S.A., Struk, I.I. & Vinogradov, A.V. (1994). High throughput and resolution compact spectrograph for the 124–250 A range based on MoSi2-Si sliced multilayer grating. Opt. Comms. 109, 1–4.Google Scholar
Ng, A., Pasini, D., CelliersP., Parfeniuk, D., Da Silva, L, &Kwan, J. (1984). Ablation scaling in steady-state ablation dominated by inverse-bremsstrahlung absorption. Appl. Phys. Lett. 45, 1046–1048.CrossRefGoogle Scholar
Obenschain, S.P., Bodner, S.E., Colombant, D., Gerber, K., Lehmberg, R.H., McLean, E.A., Mostovich, A.N., Pronko, M.S., Pawley, C.J., Schmitt, A.J., Sethian, J.D., Serlin, V., Stamper, J.A., Sullivan, C.A., Dahlburg, J.P., Gardner, J.H., Chan, Y., Deniz, A.V., Hardgrove, J., Lehecka, T. & Klapisch, M. (1996). The Nike KrF laser facility: Performance and initial target experiments. Phys. Plasmas 3, 2098–2107.CrossRefGoogle Scholar
Owadano, Y., Okuda, I., Matsumoto, Y., Matsushima, I., Koyama, K., Tomie, T. & Yano, M. (1993). Performance of the ASHURA KrF laser and its upgrading plan. Laser & Particle Beams 11, 347–351.CrossRefGoogle Scholar
Owadano, Y., Okuda, I., Matsumoto, Y., Matsushima, I., Takahashi, E., Yashiro, H., Miura, E. & Tomie, T. (1996). Super-ASHURA KrF laser program at ETL. Fusion Energy 3, 215–221. IAEA, Montreal, Canada.Google Scholar
Pawley, C.J., Gerber, K., Lehmberg, R.H., McLean, E.A., Mostovich, A.N., Obenschain, S.P., Sethian, J.D., Serlin, V., Stamper, J.A., Sullivan, C.A., Bodner, S.E., Colombant, D., Dahlburg, J.P, Schmitt, A.J., Gardner, J.H., Brown, C., Seely, J.F., Lehecha, T., Aglitskiy, Y., Deniz, A.V., Chan, Y., Metzler, N. & Klapisch, M. (1997). Measurements of laser-imprinted perturbations and Rayleigh-Taylor growth with Nike KrF laser. Phys. Plasmas 4, 1969–1977.CrossRefGoogle Scholar
Raizer, Yu.P. (1965). Heating of a gas under the action of high-power light pulse. Sov. Phys. JETP 21, 1009–1018.Google Scholar
Sedov, L.I. (1959). Similarity and Dimensional Methodes in Mechanics. New York: Academic Press.
Shaw, M.J., Bailly-Salins, R., Edwards, C.B., Harvey, E.C., Hirst, G.J., Hooker, C.J., Key, M.H., Kidd, A.K., Lister, J.M.D. & Ross, I.N. (1993). Development of high-performance KrF and Raman laser facilities for inertial confinement fusion and other applications. Laser and Particle Beams 11, 331–346.CrossRefGoogle Scholar
Sullivan, J.A., Allen, G.R., Berggren, R.R., Czuchlewski, S.J., Harris, D.B., Jones, J.E., Krohn, B.J., Kurnit, N.A., Leland, W.T., Mansfield, C., McLeod, J., McCowan, A.W., Pendergrass, J.H., Rose, E.A., Rosocha, L.A. & Thomas, V.A. (1993). KrF amplifies design issues and application to inertial confinement fusion system design. Laser and Particle Beams 11, 359–383.CrossRefGoogle Scholar
Weaver, J.L., Feldman, U., Seely, J.F., Holland, G., Serlin, V., Klapisch, M., Columbant, D. & Mostovich, A. (2001). Absolutely calibrated, time-resolved measurements of soft x rays using transmission grating spectrometers at the Nike laser facility. Phys. Plasmas 8, 5230–5238.CrossRefGoogle Scholar
Zvorykin, V.D. & Lebo, I.G. (1999). Laser and target experiments on KrF GARPUN laser installation at FIAN. Laser & Particle Beams 17, 69–88.Google Scholar
Zvorykin, V.D. & Lebo, I.G. (2000). Application of a high-power KrF laser for the study of supersonic gas flows and the development of hydrodynamic instabilities in layered media. Quant. Electron. 30, 540–544.CrossRefGoogle Scholar
Zvorykin, V.D., Bakaev, V.G., Korol', V.Yu., Lebo, I.G., Rozanov, V.B. & Sychugov, G.V. (2000). Effects of anomalous high penetration rate of high-power KrF laser radiation throughout the solid matter and shock-induced graphite-diamond phase transformation. Proc. SPIE 3885, 212–222.CrossRefGoogle Scholar
Figure 0

Micropicture of a conical SW and crater produced in Plexiglas obtained in a projection scheme with the polarized light of a copper-vapor laser.

Figure 1

Dependence of mass ablation rate on laser intensity compared for different experiments: 1: present work; 2,3,4: obtained by Ng et al. (1984); 5,6: obtained by Dahmani and Kerdjia (1991); 7,8,9: obtained by Key et al. (1983).

Figure 2

Pin-hole image of aluminum plasma in the soft X-ray range (left) and spatially resolved images of plasmas from different materials in the extreme UV range (right).

Figure 3

Electron temperature of plasmas measured by X-ray absorption in beryllium foils

Figure 4

Emission spectra of plasmas in the extreme UV range from different target materials.

Figure 5

Principle of prism raster (left) and laser radiation patterns before the focal plane and at the focal plane (right).

Figure 6

Slit-scanning images of laser interaction with solid (a), transparent (b), and foil targets (c).

Figure 7

Velocities of the plasma front and SW depending on laser intensity for atmospheric air. Solid lines: calculations for LSDW with δ = 1 (1) and δ = 0.1 (2); dashed lines: numerical simulations with allowance for the ionization process (3) and fixed ion charge Z = 3 (4).

Figure 8

Velocity of the plasma front and SW depending on air pressure for laser intensities 0.3–0.6 GW/cm2.

Figure 9

x-t diagrams for SW in atmospheric air at various laser intensities 0.2–0.8 GW/cm2.