INTRODUCTION
The achievement of laser intensities above 1018 Wcm−2 enabled the production of fast moving ions with kinetic energies approaching several tens or hundreds of MeV (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003; Robson et al., Reference Robson, Simpson, Clarke, Ledingham, Lindau, Lundh, McCanny, Mora, Neely, Wahlstrom, Zepf and McKenna2007; Flippo et al., Reference Flippo, Workman, Gautier, Letzring, Johnson and Shimada2008b). Ion beams with ultra-high energies and efficiencies provide new access to various advanced applications, including fast ignition (FI) of inertial confinement fusion (ICF) targets (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994) with heavier ions, which is currently viewed as the preferred approach to achieve high gain ICF implosions for a laser fusion power plant.
The original relativistic electron beam approach proposed for FI operation suffers from problems with localized energy deposition and focusing. Protons offer better focusing by providing almost ballistic-like trajectories, but currently, the laser-to-ion converter foils used for proton ion generation give proton beam fluxes several orders of magnitude below the total fluxes required for practical FI (Snavely et al., Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell2000; Fernández et al., Reference Fernández, Hegelich, Cobble, Flippo, Letzring, Johnson, Gautier, Shimada, Kyrala, Wang, Wetteland and Schreiber2005). Special conical conversion foil configurations are under study to help close this intensity gap (Flippo et al., Reference Flippo, d'Humieres, Gaillard, Rassuchine, Gautier, Schollmeier, Nurnberg, Kline, Adams, Albright, Bakeman, Harres, Johnson, Korgan, Letzring, Malekos, Renard-LeGalloudec, Sentoku, Shimada, Roth, Cowan, Fernandez and Hegelich2008a). Heavier ions, such as carbon, have been proposed and also studied to further improve focusing and ion yields, but much higher laser intensities needed for this approach will not be available in the immediate future (Fernández et al., Reference Fernández, Honrubia, Albright, Flippo, Gautier, Hegelich, Schmitt, Temporal and Lin2009).
Deuterons have been considered for FI as well (Bychenkov et al., Reference Bychenkov, Rozmus, Maksimchuk, Umstadter and Capjack2001; Shmatov, Reference Shmatov2007; Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou2009; Tikhonchuk et al., Reference Tikhonchuk, Schlegel, Regan, Temporal, Feugeas, Nicolaï and Ribeyre2010). Our recent calculation has shown that deuterons would not only provide improved ballistic focusing, but also fuse with the target fuel (both D and T) as they slow down (Yang et al., Reference Yang, Miley, Flippo and Hora2011a), providing a “bonus” energy gain. Depending on the target plasma conditions, this added fusion gain can feature a significant contribution (Shmatov Reference Shmatov2004; Yang et al., Reference Yang, Miley, Flippo and Hora2011a). For instance, our recent estimates have shown that an average 30% extra energy can be gained from deuterons with 1-MeV initial energy and 12% from deuterons with 3-MeV initial energy (Yang et al., Reference Yang, Miley, Flippo and Hora2011a). Thus, if a high flux of deuterons can be achieved, deuteron beam driven FI could turn quite attractive. Various materials for the converter foil have been studied for deuteron beam generation. Some studies show that a deuteron beam (as well as a triton beam) can be generated by ponderomotive acceleration of deuterons (or tritons) in the overcritical plasma formed by the laser interaction with the ICF target itself (Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou2009; Tikhonchuk et al., Reference Tikhonchuk, Schlegel, Regan, Temporal, Feugeas, Nicolaï and Ribeyre2010). However, the ion flux obtained in that manner is not adequate for FI without a drastic increase in laser intensity well beyond that of current lasers (Fernández et al., Reference Fernández, Albright, Flippo, Hegelich, Kwan, Schmitt and Yin2008; Naumova et al., Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou2009). The converter foil approach overcomes the propagation instability issues involved in the direct coronal interaction (Deutsch, Reference Deutsch2003), thus, it is considered to be the preferred method. A deuteron beam has been generated experimentally using a deuterated polymer layer coated on the substrate surface of a converter foil. However, the deuterated polymer contains a high density of carbon that is also accelerated, reducing the deuterium intensity and extraction efficiency (Nemoto et al., Reference Nemoto, Maksimchuk, Banerjee, Flippo, Mourou, Umstadter and Bychenkov2001).
In our previous study (Yang et al., Reference Yang, Miley, Flippo and Hora2011a), a novel cluster-based converter foil was proposed for deuteron beam generation. In this type of converter foil, deuterium is volumetrically loaded into the palladium lattice, and forms a condensed matter state — named “clusters” — in the palladium lattice defects. These clusters contain a hundred or so deuterium ions in a tightly bound almost metallic state. Palladium is much heavier than deuterium, thus unlike the carbon in the deuterated polymer, it has a much higher probability of being screened by the deuterons, meaning that deuterons will outrun palladium and take most of the energy with them. Moreover, volumetric loading offers a high total number of source deuterons. If all these deuterons can be utilized as in the relativistic transparent case (Henig et al., Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernández, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich2009), this cluster converter foil has the potential to achieve the deuteron yield needed for hot spot ignition. In addition, the yield required for ignition is reduced for deuterons versus protons due to the “bonus” energy from the direct fusion between the deuteron beam and the D-T in the target. We previously presented a calculation to estimate the magnitude of this “bonus” energy gain under various deuteron energies and target temperatures (Yang et al., Reference Yang, Miley, Flippo and Hora2011a). But that calculation used a first order approximation that assumed the deuterons heating of the hot spot occurs at certain defined energies into the hot spot at some prescribed temperatures as opposed to a continuous time heating profile. Hence, a more detailed calculation on hot spot heating is described here using a more realistic deuteron beam energy distribution and a continuous hot spot temperature rise. In this study, the deuteron beam energy distribution is estimated based on earlier measurements of proton beams generated by the conversion foil method using the TRIDENT petawatt pulse laser at LANL (Flippo et al., Reference Flippo, Gaillard, Kluge, Bussmann, Offermann, Cobble, Schmitt, Bartal, Beg, Cowan, Gall, Gautier, Geissel, Kwan, Korgan, Kovaleski, Lockard, Malekos, Montgomery, Schollmeier and Sentoku2010). The hot spot heating process by this assumed deuteron beam and first order heating dynamics is then employed in calculating the hot spot heating and the “bonus” energy. This study also provides further insight into how the energy produced by deuteron beam-target fusion can provide significant “extra” heating of the hot spot. A further analysis of how a converter foil using ultra-high-density cluster materials can help to achieve the yield requirements for ignition is presented.
DEUTERON BEAM ENERGY SPECTRUM ESTIMATE
When the intensity is sufficient, short-pulse laser interaction with solid foils have been shown in a number of laboratories to generate an electron beam that is typically accelerated to highly relativistic energies. A significant number of hot electrons propagate through the foil and emerge from rear surface (opposite side from the entering laser beam) to form a very high electrostatic field. This electrostatic field is sufficient to ionize atoms at the rear side of the converter foil (Pennington et al., Reference Pennington, Brown, Cowan, Hatchett, Henry, Herman, Kartz, Key, Koch, MacKinnon, Perry, Phillips, Roth, Sangster, Singh, Snavely, Stoyer, Stuart and Wilks2000; Murakami et al., Reference Murakami, Kitagawa, Sentoku, Mori, Kodama, Tanaka, Mima and Yamanaka2001; Bari et al., Reference Bari, Sheng, Wang, Li, Salahuddin, Nasim, Naz, Gondal and Zhang2010). This mechanism was termed target normal sheath acceleration (TNSA), which generally explains the acceleration process at the rear side of the target surface, and is a main mechanism of accelerating ions into very high energy. Some early experiments have shown that accelerated protons and deuterons could also originate from the front side (the side facing the laser) of the thin-film converter foil (Maksimchuk et al., Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000, Reference Maksimchuk, Flippo, Krause, Mourou, Nemoto, Shultz, Umstadter, Vane, Bychenkov, Dudnikova, Kovalev, Mima, Novikov, Sentoku and Tolokonnikov2004; Nemoto et al., Reference Nemoto, Maksimchuk, Banerjee, Flippo, Mourou, Umstadter and Bychenkov2001). This type of acceleration has been explained by a ponderomotive process. The laser's ponderomotive force can exert a pressure on the target electrons driving them away from regions of highest intensity into the target. The relatively heavy ions are unaffected by the laser fields directly, but respond to the electric field due to the electron displacement (Willingale et al., Reference Willingale2011). When the laser pulse is circularly polarized, it quenches the fast electron generation, and accelerates ions by purely ponderomotive force, and then at moderate laser intensities the radiation pressure dominance is obtained. In this case, the ions accelerated ponderomotively can display specific feature such as high efficiency, large density and good collimation (Liseikina et al., Reference Liseikina, Prellino, Cornolti and Macchi2008). Further experiments have shown that by removing the contaminant layer on the converter foil surfaces, the heavier ions at the front and back sides can be used in unison to change and even increase the contributions of either side (Willingale et al., Reference Willingale2011). These results suggest that depending on the parameters of both the target and the laser, ions at the front surface, within the foil (i.e., volumetric ions) and at the rear side can all be accelerated in the forward direction (laser light transport direction), although acceleration mechanism for ions in distinct regions exhibit different acceleration mechanisms.
To test the effect of our cluster concept, proof-of-principle shots with the cluster converter foils were recently performed on the TRIDENT 200 TW laser at LANL (Yang et al., Reference Yang, Miley, Flippo, Gaillard, Offermann, Hora, Gall, Burris-Mog, Rassuchine, Plechaty and Ren2011b) The results showed that deuterium ions were extracted and accelerated to energies over 5 MeV. This estimate came out from the use of a titanium foil in the beam path prior to it impinging on the beam energy analyzer. According to stopping and range of ions in matter calculation, deuterons less than 5 MeV were blocked by a 100-μm Titanium foil placed at the face of the ion energy analyzer. The purpose of this foil was to block carbon ions over 100 MeV in order to avoid their interference with deuterons) and up to about 10 MeV. This deuteron acceleration was achieved without attempting to remove any hydrocarbon contamination from the foil surface, thus a large amount of laser energy was lost in the acceleration of undesired carbon ions and protons (Yang et al., Reference Yang, Miley, Flippo, Gaillard, Offermann, Hora, Gall, Burris-Mog, Rassuchine, Plechaty and Ren2011b). Therefore, the deuterons that were observed above 5 MeV could well have reached higher energies without this extraneous energy drain. As the D-clusters, i.e., the deuteron source, are located well inside the palladium volume rather than directly on the front and rear surface, these results, together with the previous finding of deuteron and proton acceleration from the front face of the foil noted above, suggest that ions beneath the front and rear surface can be accelerated when a suitable laser condition is fulfilled. Thus, concerns that the laser interaction mechanism might not provide good coupling to the unique D-clusters in the foil volume especially near the surfaces do not appear to be a major issue. Still, this is only a preliminary result and much more attention to this volumetric coupling deserves investigation.
The deuteron energy spectrum shown in Figure 1 was estimated by extrapolation of the proton energy spectrum achieved with TRIDENT short pulse 200-TW laser at LANL (Flippo et al., Reference Flippo, Workman, Gautier, Letzring, Johnson and Shimada2008b, Reference Flippo, Gaillard, Kluge, Bussmann, Offermann, Cobble, Schmitt, Bartal, Beg, Cowan, Gall, Gautier, Geissel, Kwan, Korgan, Kovaleski, Lockard, Malekos, Montgomery, Schollmeier and Sentoku2010). The proton energy and number were deconvoluted in a process termed radiochromic film imaging spectroscopy (Nurnberg et al., Reference Nurnberg, Schollmeier, Brambrink, Blazevic, Carroll, Flippo, Gautier, Geissel, Harres, Hegelich, Lundh, Markey, McKenna, Neely, Schreiber and Roth2009). The deuteron spectrum of Figure 1 extrapolates that result based on the following assumptions. First, according to the recent experiments, one can accelerate the deuterons to about the same energies as protons if protons are removed, or to about half their energy if the protons are still present (Willingale and et al., 2011). However, to date, it is still very difficult to completely remove the hydrocarbon contaminant layer. Thus, we assume hydrocarbon contaminant layer has been significantly reduced from the deuterium converter foil, so deuterons will be effectively accelerated by the ideal electrostatic field arising from electron acceleration. Then the deuteron energy spectrum will have a shape that is similar to the measured proton energy spectrum, but with a slightly lower maximum energy. Second, as deuterons are mainly accelerated in the volume, the deuterium beam's high-energy cut-off will be shifted down further due to energy loss in the foil compared with the high energy protons that mainly arise from the rear side of the foil surface. Third, again due to volume loading, we assume deuterons have a higher source density and thus will have a higher yield at each energy level than protons that are generated from the surface layer and suffer a “depletion effect” (i.e., the source is depleted before the acceleration force decays) that limits their yield (Fernández et al., Reference Fernández, Albright, Flippo, Hegelich, Kwan, Schmitt and Yin2008). Last, according to the proton beam energy distribution function, the number of protons in the high energy tail (from ca. 30 to 50 MeV) is several orders of magnitude less than those at the lower energy. Thus, we ignore the high energy tail and consider only an exponential shape as shown in Figure 1. The 20-MeV high-energy cut-off for deuterons is a rather conservative assumption due to the concern listed above. The total energy of the deuteron beam assumed in Figure 1 is 5.02 × 1016 MeV, which is slightly lower than the estimated ignition requirement that to ignite the fuel — about 10 kJ or 6.24 × 1016 MeV. This is so because it will be shown later that in some cases the hot spot can still be created with this estimated function.
Fig. 1. An estimated deuteron beam energy spectrum based on a proton beam energy spectrum (Inset) experimentally achieved from TRIDENT laser at LANL (Flippo et al., Reference Flippo, Workman, Gautier, Letzring, Johnson and Shimada2008b, Reference Flippo, Gaillard, Kluge, Bussmann, Offermann, Cobble, Schmitt, Bartal, Beg, Cowan, Gall, Gautier, Geissel, Kwan, Korgan, Kovaleski, Lockard, Malekos, Montgomery, Schollmeier and Sentoku2010). The X-axis represents the ion energy levels, and the y-axis represents the number of ions in a 1 MeV bin at each ion energy level. The deuteron beam energy spectrum has a shape similar to the proton beam but a lower high-energy cutoff. The yield of this deuteron beam is normalized to meet the ignition requirement for deuteron-driven FI of a DT ICF target (~1016 level). This yield is lower than what would be needed without the added “bonus” energy heating. This assumes that the volumetric deuterium loading with D-clusters enables very high yields compared to surface coated converter foils that suffer a “saturation” limit.
HOT SPOT HEATING AND THE BONUS ENERGY ESTIMATE
The parameters that affect hot spot heating process include the initial density and the temperature of the compressed fusion fuel just prior to its interaction with the FI ions or electron beam. Studies by Fernández et al. (Reference Fernández, Albright, Flippo, Hegelich, Kwan, Schmitt and Yin2008) show that for high gain FI, the assembled fuel should be compressed to a mass density in the range ρ = 300–500 g/cm3, in order to keep the required ignition energy and the fusion yield at manageably small levels. The initially compressed ICF target temperature is typically found to be about1 keV, while complete burn propagation requires that the hot spot reaches an average temperature ≥10 keV (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001; Hora et al., Reference Hora, Miley, Yang and Lalousis2011). Another key parameter that affects the hot spot heating process is the quality of the laser beam focusing which in turn determines the size of the hot spot. The radius of the hot spot should be large enough to prevent the fusion product alpha particles from escaping, but it shouldn't be too large, as more energy must be deposited in order to heat a larger hot spot (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks, Yasuike, Ruhl, Pegoraro, Bulanov, Campbell, Perry and Powell2001; Hora et al., Reference Hora, Miley, Yang and Lalousis2011). According to Atzeni's (Reference Atzeni1999) model study, at ρr b ≈ 0.3–0.6 g/cm2 (r b is ion beam focusing radius and ρ is the fusion fuel target density), the minimum igniter beam energy, power, and intensity required for FI are only weakly affected by the ion stopping range ℛ over a reasonably wide interval 0.15 ≤ ℛ ≤ 1.2 g/cm2. Here ℛ = ρL, and L is the hot spot length at the ignition ion beam transport direction. Then the optimal size can be conveniently stated in terms of ℛ Too large an ℛ yields a large hot spot volume, requiring extra hot spot energy to reach the ignition temperature, while a too small ℛ yields too small a hot spot which is not able to induce burn propagation. An experimental setup is plotted in Figure 2 to further illustrate these parameters.
Fig. 2. (Color online) An illustration for the parameters L, r b, and ρ in a setup of the FI experiment. L is the hot spot length at the ignition ion beam transport direction (Atzeni, Reference Atzeni1999), and r b is ion beam focusing radius. ρ represents the densities of both target and the hot spot as researchers have found that the density of the hot spot does not change significantly despite the significant increase of the temperature at the hot-spot region during the hot-spot formation (Honrubia et al., Reference Honrubia, Fernandez, Temporal, Hegelich and Meyer-ter-Vehn2009; Honrubia & Meyer-ter-Vehn, Reference Honrubia and Meyer-ter-Vehn2009).
The deuterium energies and yield assumed in Figure 1 are used to estimate the hot spot heating process. The equation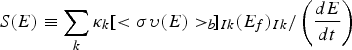 
(Eq. (2) in Yang et al., Reference Yang, Miley, Flippo and Hora2011a) was used to calculate the bonus energy during the ion deposition of each energy level, where (συ)Ik is the fusion reactivity for the injected ion I of species k having atomic fraction κk in the target, (E f) Ik is the corresponding energy released per fusion, E is the deuteron energy, and t is the time. Also, as discussed in Yang et al. (Reference Yang, Miley, Flippo and Hora2011a), the bonus energy contribution from D-D fusion during the burn is orders of magnitude smaller than that from the D-T fusion portion, thus only the D-T part is considered here. ρr b ≈ 0.45 or 0.6 g/cm2 is assumed so that the D-T fusion product (helium 4) can be mostly stopped within this region. Moreover, a core plasma with single flat ρ = 300 g/cm3 is assumed. This assumption simplifies the calculation and is thought to provide a reasonable first estimate of the hot spot behavior. The specific heat of the D-T fuel is assumed to be 115.8 MJ/(g × keV) (Frolov, Reference Frolov1998), and the total volume is calculated using equation V = π × r b2 × L, where L = ℛ/ρ. We then know the heat capacity of the hot spot by assuming ℛ = 1.2 g/cm2. In the calculation, a number of deuterons in a 1 MeV bin at each energy level are deposited as an energy “bunch” into the hot spot with hotter ions arriving at the target first. The hot spot temperature is calculated each time after one energy “bunch” is deposited by adding the incremental temperature due to each deposition to the temperature before the deposition. This first order calculation is not intended to give a precise description of the dynamic ignition process, but only to provide insight into how the bonus energy gained by the deuterium beam-target fusion contributes to the ignition of the hot spot (A computationally intensive three-dimensional simulation code evaluation would be needed to more accurately treat the detailed dynamics involved in this process). Results are used to evaluate the contribution of the “bonus” energy by comparing the total deuteron beam energy required for ignition with and without this added energy.
Figure 3 shows the hot spot heating process without (Fig. 3A) and with (Fig. 3B) considering the “bonus” energy, by assuming that the initial temperature of the D-T fuel is 1 keV. Under these conditions, the highest bonus energy gain occurs with lower energy deuterium ions in about the 3-MeV range. At first thought, the deuteron energy distribution with a very wide energy spread shown in Figure 1 would not appear to be very effective for this process since we aim at restricting the ion stopping within hot spot extension. However, the dynamic process during heating allows the lower energy ions to progressively penetrate into the target hot spot region once the higher energy component initiates heating. As discussed in previous study (Yang et al., Reference Yang, Miley, Flippo and Hora2011a), when a deuteron beam is directed toward the D-T fuel, the higher energy deuterons arrive at the cold fuel in the hot spot region first with an energy appropriate for stopping in the desired volume, increasing its temperature. Then the lower energy deuterons arrive such that the elevated temperature allows good penetration despite the lower energy. They then produce a prominent fusion gain through beam-target reactions at the new, elevated temperature (Tikhonchuk et al., Reference Tikhonchuk, Schlegel, Regan, Temporal, Feugeas, Nicolaï and Ribeyre2010). Without the bonus energy and with the deuteron yield assumed in Figure 1, the highest temperature that the hot spot can eventually reach is 5.65 keV for ρr b = 0.6 g/cm2, and 9.24 keV for ρr b = 0.45 g/cm2, meaning that in both cases, the hot spot cannot reach required temperature (≥10 keV). The possible “bonus” energy was then calculated at each deposition, and was added back to the hot spot heating process at each deposition. The results are shown in Figure 3B. It can be seen that the ultimate temperature of case ρr b = 0.45 g/cm2 is well above 10 keV, suggesting that the hot spot should be ignited with this assumed yield only when the bonus energy is considered. For the case of ρr b = 0.6 g/cm2, the temperature also increases by up to 70% when compared with the no-bonus-energy condition. Both these results emphasize the advantage of the added “bonus” energy.
Fig. 3. Deuteron driven Hot spot heating process without (a) and with (b) the contribution from the bonus energy due to deuterium-beam-target fusion.
The above calculation is based on the assumption that all of the deuterons can be stopped in the hot spot (within ℛ = 1.2 g/cm2). According to our previous study (Yang et al., Reference Yang, Miley, Flippo and Hora2011a), 10-MeV deuterons can be stopped within ℛ = 1.2 g/cm2 when the hot spot temperature is below 5 keV, and 3-MeV deuterons (lower end of the spectrum) can be deposited within ℛ = 1.2 g/cm2 when the hot spot temperature is below 10 keV, meaning that deuterons with energy in between 3 MeV and 10 MeV can be stopped within ℛ = 1.2 g/cm2 when the hot spot temperature lies between 5 keV and 10 keV. Also, by expending our previous calculation (Yang et al., Reference Yang, Miley, Flippo, Gaillard, Offermann, Hora, Gall, Burris-Mog, Rassuchine, Plechaty and Ren2011b) (results are not shown here), we know that deuterons with energy between 10 MeV and 20 MeV can all be stopped within ℛ = 1.2 g/cm2 when the hot spot temperature remains below 3 keV. From Figure 2 we can see that all these conditions have been met during the hot spot heating, suggesting ℛ = 1.2 g/cm2 is a valid assumption in this hot spot heating calculation.
To elaborate more on the contribution of the “bonus” energy achieved, the bonus energy achieved by deuterons of 1 MeV, 2 MeV, 3 MeV, and its percentage relative to the respective total deuteron-beam energies assumed are listed in Table 1. The total deuteron energy at each energy level is the product of the defined energy level and the number of deuterons at this energy level (see Fig. 1). The reason that we care only about this deuteron energy range is that according to our calculations (Yang et al., Reference Yang, Miley, Flippo and Hora2011a), the bonus energy production is negligible when the deuteron energy is high and the hot spot temperature is low.
Table 1. Bonus energy during hot spot heating process using first order hot spot heating estimation
From Table 1, we see that at fixed R and ρ, the bonus energy increases with decreasing r b. This is so because a smaller r b gives a smaller hot spot volume and smaller heat capacity, thus the hot spot temperature rises faster at each deuteron energy level. Comparison of the current results with those in our previous study (Yang et al., Reference Yang, Miley, Flippo and Hora2011a) shows that the “bonus” energy contribution from a more realistic deuteron spectrum used here is not as large, percentage-wise, as that from the previously assumed low energy (1 MeV to 3 MeV) mono-energetic deuterons. Still, the added energy, is significant, and remains an important contribution to the hot spot heating.
ACCELERATING ULTRA-HIGH-DENSITY DEUTERIUM CLUSTER MATERIAL BASED CONVERTER FOIL
Currently, the clusters in the materials we achieved experimentally have deuterium density exceeding 1024/cm3 (Miley & Yang, Reference Miley and Yang2009; Miley et al., Reference Miley, Yang, Heinrich, Flippo, Gaillard, Offermann and Gautier2010). However, the cluster sites presently occupy only about 0.1% of the volume of the host material, meaning the packing-fraction is relatively low (here packing fraction means clusters per cubic centimeter). In this case, the FI ignition requirement of 1018 Deuterons/cm2 for about 1 mm2 ion-beam focusing area (or the effective area of the converter foil) (Fernández et al., Reference Fernández, Albright, Flippo, Hegelich, Kwan, Schmitt and Yin2008, Reference Fernández, Honrubia, Albright, Flippo, Gautier, Hegelich, Schmitt, Temporal and Lin2009) would be achieved in a 1 μm thick target foil if 100% of the deuterons in the volume can be accelerated; alternately a thicker target foil would be needed if a smaller percentage of deuterons is accelerated. Nevertheless, the foil thickness cannot be arbitrarily increased, as with different laser parameters, such as contrast ratio and pulse duration, the acceleration process will be altered when using target foils of different thickness (Maksimchuk et al., Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000; Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004; Ceccotti et al., Reference Ceccotti, Lévy, Popescu, Réau, D'Oliveira, Monot, Geindre, Lefebvre and Martin2007). For lasers of different prepulse durations, an optimal thickness of the target exists for maximum proton cut-off energy (Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004; Ceccotti et al., Reference Ceccotti, Lévy, Popescu, Réau, D'Oliveira, Monot, Geindre, Lefebvre and Martin2007): when targets are thinner than the optimal thickness, ponderomotive acceleration dominates, and the rear side TNSA mechanism is suppressed due to the formation of a plasma density gradient at the rear side of the target, thus only the front side acceleration is active; for target thicknesses above the optimal value, protons are accelerated from both target surfaces with higher cutoff energies achieved from rear side acceleration (Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004). Therefore, at longer prepulse duration, the maximum proton energies are achieved with thicker foils. As an example, the highest proton cut-off energy was achieved respectively from 2-µm-thick foil for prepulse duration of 0.5 ns and from ca. 8-µm-thick foil for prepulse duration of 2.5 ns. When the prepulse length is fixed, higher laser intensity gives higher maximum proton energy. For a high-contrast laser of constant energy, different pulse duration will produce different proton cutoff energy for the targets of certain thickness with the varied efficiency of the laser-plasma coupling and maximum obtainable electron temperature (Flacco et al., Reference Flacco, Sylla, Veltcheva, Carrié, Nuter, Lefebvre, Batani and Malka2010). Hence, by adjusting laser parameters, bulk accelerating deuterium cluster material of micron or sub-micron thickness is highly feasible.
When the TNSA sheath field is strong enough, it penetrates deeper into the target. In addition, high-intensity effect such as relativistic transparency can amplify acceleration from the bulk (Henig et al., Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernández, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich2009). Maximizing both effects will finally determine the thickness of a deuterium laden target and should lead to significant volume acceleration. Currently, our goal is to find techniques to achieve 10 times more packing fraction in the converter foil material, which will provide a conservative deuteron-loading that would be advantageous in case the extraction percentage is not as high as hoped. In any case these estimates suggest that the present D-cluster foils are not far from what is needed for actual FI experiments and applications. Much more study is requested, however, to fully understand the acceleration process with clusters in order to accurately evaluate the potential for FI with this approach. Key development issues include the cluster volume fraction that can be achieved with nano-manufacturing of the base materials for the foils, the deuteron energy spectrum from such foils, and the deuteron extraction efficiencies.
SUMMARY
This study estimates the dynamics of the hot spot heating process in a pre-compressed D-T fuel by a high-energy deuteron beam. The deuteron beam spectrum was estimated according to an experimental proton beam energy function achieved using the TRIDENT short-pulse 200 TW laser. A “bonus” energy effect owing to beam-target fusion can provide a significant contribution to hot spot heating — with added hot spot heating as high as 12.73% of the required total. Although these results are only a first estimate, they provide important insight into the possible significance of the bonus energy gained by the beam-target fusion to the hot spot heating. Future studies should give more detailed consideration to the stopping range changes during the heating process and temperature rise, but this will require rather elaborate simulation studies with a code such as LASNEX. In addition, the initial evaluation of our ultra-high-density deuterium cluster material indicates that with its volumetric loading this material has the potential to produce deuteron yields needed meeting the FI ignition requirement. Future effort is being devoted to methods for increasing the cluster packing fraction in the converter foil. Since the foil thickness is an important factor in the deuteron yield and energy spectrum, further studies of the optimum foil thickness are also underway. However, on the basis of the very preliminary TRIDENT experiments noted, plus these scoping calculations, this approach continues to appear as a potential contender to any effective FI.
ACKNOWLEDGMENT
Support for parts of the work by a NPL Associate INC Plasma Physics grant and by the New York Community Trust was essential to the effort. Kirk A. Flippo is funded through LANL LDRD under DOE contract number DE-AC52-06NA25396.
