1. INTRODUCTION
In recent years, intense short pulse lasers are available with the development of the chirped pulse amplification (CPA) technique (Mourou et al., 1998; Strickland & Mourou, 1985). The development of the CPA laser technology has stimulated various particle acceleration schemes (Esarey et al., 1995; Glinec et al., 2005; Kawata et al., 1991; Kong et al., 2000; Pommiers & Lefebvre, 2003; Malka et al., 1997; Sakami & Mima, 2004; Shorokhov & Pukhov, 2004; Steinhauer & Kimurai, 1992; Scully & Zubairy, 1991; Tajima & Dawson, 1979). At the same time, generation of attosecond electron beams are actively researched (Stupakov & Zolotorev, 2001; Naumova et al., 2004; Masuda et al., 2005), and these attosecond electron beams can be used by studies of atomic dynamics, generation of X-rays, etc. in attophysics. In this paper, we propose a generation of high energy and high density attosecond electron bunch by a focused intense pulse TEM (1,0) + TEM (0,1)-mode laser with a plasma separator in vacuum. A TEM (0,0)-mode laser is widely used for particle acceleration. The TEM (0,0)-mode laser has a peak in its field strength at the central axis. Therefore, the electrons are accelerated by the longitudinal ponderomotive force at the head of laser pulse. However, the electrons are scattered by the transverse ponderomotive force in the transverse direction. This is one of the problems in the electron acceleration by the laser. In this paper, in order to suppress the transverse scattering, we employ the TEM (1,0) + TEM (0,1)-mode laser (Kawata et al., 2005; Kong et al., 2003). The TEM (1,0) + TEM (0,1)-mode laser has a ring-shaped intensity peak in the radial direction. The electrons are confined near the central axis by the transverse ponderomotive force. The advantage of our mechanism includes a generation of high density electron beam. We found that the TEM (1,0) + TEM (0,1)-mode laser give a good tool to suppress the transverse scattering of the electrons and to compress the electron beam in transverse. Furthermore, the TEM (1,0) + TEM (0,1)-mode laser has a longitudinal electric field at the laser axis; the electrons are accelerated by the longitudinal electric field near the central axis. In addition, if the velocity of the initial electrons is high enough, an interaction length l between the electrons and the laser is relatively long (l ∼ zR), and the electrons can stay in the acceleration phase of the laser one cycle (Miyazaki et al., 2005). Here zR = πw02/λ is the Rayleigh length of the laser, w0 is the spot size at the laser focal point, and λ is the wavelength of the laser. However, the electrons are dropped off from the acceleration phase in the laser one cycle by the difference between the electrons velocity and the laser phase velocity. As the results, the electrons experience a deceleration and have an energy spread. After all, the density of the electrons generated by the laser becomes lower. In this paper, in order to prevent the deceleration and the electron spread, we also employ the overdense slab plasma separator (Miyauchi et al., 2004; Sakai et al., 2005; Vshivkov et al., 1998; Yu et al., 2000). Figure 1 shows the electron acceleration mechanism by the plasma separator. At first, the electrons are accelerated and confined by the TEM (1,0) + TEM (0,1)-mode laser (Fig. 1a). Then, before the electrons are decelerated by the laser, we set the plasma separator. Only the laser is reflected by the plasma separator and only the electrons pass through the plasma separator. After the electrons pass through the plasma separator without a large electron energy loss and the density lowering, the electron density is kept high, because the laser deceleration phase does not influence the electrons in our case.

Electron acceleration mechanism by using the plasma separator. (a) Before the interaction between the laser and the electrons. (b) After the interaction between the laser and the electrons, and only the electrons pass through the plasma separator.
2. SIMULATION MODEL
The transverse electric field of the TEM (1,0) + TEM (0,1)-mode laser propagating in the direction of z is given by

where, E0 is the amplitude of the electric field, w0 is the minimum spot size of the laser,

is the transverse radius, k is the laser wave number, ω is the laser angular frequency, Lz is the pulse length of the laser.

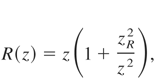
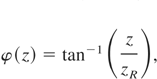
are the laser spot size, the laser curvature radius and the Gouy phase factor of the laser, respectively. The other electric and magnetic fields components are expressed by
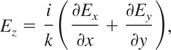
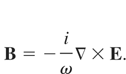
The paraxial approximation, which is proved to work well for a large focus scale of kw0 > 50 (Cao et al., 2002), is used to derive full expressions of the field. The Maxwell equation requires symmetry of the electric components and the magnetic components. However, the terms of Ex [∂f (z − ct)/∂z] and Ey [∂f (z − ct)/∂z] appears in Bx and By, and break the symmetry of E and B. We follow the idea of Davis (1979) to build the symmetric field description for the laser field.
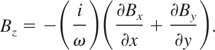
The relativistic equation of motion,
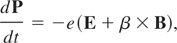
is solved by the fourth-order Runge–Kutta method. Here P is the electron momentum, e is the electron charge, β is the electron velocity in units of c and me is the electron mass.
We select the initial electron energy of γ ∼ 3 so that the electrons are well accelerated and density of the electron beam accelerated is high near the laser focal point. The number of γ0 ∼ 3 is just selected as typical initial electron energy. The initial electron bunch density is nb0 ∼ 1.84 × 1011 cm−3. The size of the initial electron bunch is 150Lz in the longitudinal direction and 20w0 in the radial direction. The initial electrons are in the Maxwell distribution with the temperature of Te = 1 eV at the initial time. The center of the electron bunch coincides with the laser intensity peak at the laser focal point at t = 0.
3. SIMULATION RESULTS
3.1. Electron acceleration by TEM (1,0) + TEM (0,1)-mode laser without plasma separator
In this subsection, we show the electron acceleration by the TEM (1,0) + TEM (0,1)-mode laser without the plasma separator. Figure 2 shows the typical electron trajectories in the z-x plane and the energy histories in the z direction without the plasma separator. The laser parameters are a0 = 5, λ = 0.8 μm, w0 = 20λ, and Lz = 5λ. Here a0 is the dimensionless laser amplitude parameter. The electrons are confined well and are accelerated by the longitudinal electric field at the central axis near z = 1000λ. After the electrons pass z = 2000λ, some electrons move from the inside of the laser envelope and are decelerated by the laser, because the electrons are sifted to the laser deceleration phase (Fig. 2a and Fig. 2b). Figure 3 shows the maps of electrons in the z-x plane and the electron energy γ maps at the time of t = 1000λ/c and t = 10000λ/c. In Figure 3a, the electrons are confined near the central axis. The peak electron number density is nb/nb0 ∼ 276. In Figure 3b, the electrons are accelerated at the front of the laser pulse. The maximum energy of the electron is γ ∼ 302 at t = 1000λ/c. In Figure 3c, the electrons move to the laser deceleration phase and are scattered by the laser. The density of the electron becomes lower. The maximum energy of the electron is γ ∼ 179 at t = 10000λ/c (Fig. 3d).

A typical case of electrons behavior without the plasma separator. (a) The electron trajectories in the z-x plane. (b) The electron energy histories in the z direction. The laser parameters are a0 = 5, w0 = 20λ, and Lz = 5λ.

Electron distributions without the plasma separator. Electrons distributions in z-x plane at the time of (a) t = 1000λ/c and (c) t = 10000λ/c. Electron energy distributions in the z direction at the time of (b) and (d) t = 1000λ/c and t = 10000λ/c.
3.2. Electron acceleration in the case with the plasma separator
In this subsection, we present the simulation results of the electron acceleration in the case with the plasma separator. We also show the effect of the plasma separator position on the electron acceleration. Figure 4 shows the electron trajectories in the z-x plane and the energy histories in the z direction. The electron initial positions shown in Figure 4 are the same as the electrons shown in Figure 2. The plasma separator is put at z = 10000λ/c. Before the electrons pass through the plasma separator, the electrons are confined near the central axis and accelerated by the longitudinal electric field of the acceleration phase. After the electrons pass through the plasma separator, the electrons are not scattered, and the electrons do not enter the laser deceleration phase, because the laser is reflected by the plasma separator and the electrons do not receive the influence of the laser deceleration phase (Fig. 4a and Fig. 4b). Here we do not include the response of the plasma separator and we assume that the plasma separator effect include in the simulations by eliminating the laser field after the plasma separator positions. In our previous paper (Miyauchi et al., 2004), we confirmed that the plasma separator response effect is not critical for the separation and the electron acceleration. Figure 5 shows the histories of the electron peak density and the peak energy density with the plasma separator (a solid line), and without the plasma separator (a dotted line). In the case with the plasma separator, the plasma separator is put at 1000λ in the z direction. Before t = 1000λ/c, the electrons are gathered by the acceleration phase of the laser, and the density of the electrons rises rapidly. After t = 1000λ/c, when the plasma separator is not employed, the density of the electrons gradually falls, because the electrons move to the deceleration phase of the laser. The electron number density is lower than the initial density at t = 1000λ/c (Fig. 5a). On the other hand, in the case with the plasma separator, the density of the electrons does not decrease much after the plasma separator. In Figure 5b, in the case without the plasma separator, the peak electron energy density also falls gradually, because the electrons are decelerated and scattered. Figure 6a shows the snapshot of the electrons in the z-x plane, and Figure 6b presents the electron energy distribution in the z direction at t = 10000λ/c. Only the laser is reflected by the plasma separator and the electrons accelerated pass through the plasma separator. Therefore, when the plasma separator is employed, the electrons are confined near the central axis and the electron energy is kept higher than that in the case without the plasma separator. Figure 7a shows the density of the electrons accelerated and Figure 7b shows the electron density profile at the x = y = 0 in the z direction at t = 10000λ/c. The high density area exists on the central axis. The peak electron number density is nb = 2.97 × 1012 cm−3 that is 16.1 times the initial density. The bunch size is 0.17λ (454 attosecond) in the z direction and 12.5λ in the radial direction. The rms emittances of the electron bunch are εx = 7.94 × 10−2π mm mrad and εy = 7.40 × 10−2π mm mrad, and the average energy of the electron bunch is γ ∼ 221. Figure 8 shows the energy spectrum of the electron bunch at t = 10000λ/c. The momentum spread of the electron bunch is 3.66%. Figure 9a shows the relation between the plasma separator position and the peak electron number density. Figure 9b shows the relation between the separator position and the electron energy density of the electron bunch. The results shown in Figure 9 are the optimal position of the plasma separator. When the separator is put left in z from the optimal position, the electrons are not gathered, and accelerated enough by the laser. Therefore, the electron number density and the energy density become lower. When the plasma separator is employed right, the electrons are scattered and decelerated by the laser, and the density of the electrons and the energy density are lower than those at the optimal position (Fig. 9a and Fig. 9b). However, Figure 9 shows that the electron number density and the energy density are relatively insensitive to the plasma separator position in practical.

The electron behavior in the case with the plasma separator. The plasma separator is located at z = 1000λ/c. (a) The Electron Trajectories in the z-x plane. (b) The electron histories in the z direction.

The electron density histories with the plasma separator (a solid line) and without the plasma separator (a dotted line). (a) The electron number density. (b) The electron energy density.

The electron distributions at the time of t = 10000λ/c. (a) The electron distribution in the z-x plane. (b) The electron energy distribution in the z direction.

The electron number density maps at the time of t = 10000λ/c. (a) The electron number density distribution in the z-x plane. (b) The electron number density distribution at x = y = 0 in the z direction.

The electron energy spectrum at the time of t = 10000λ/c. The electrons are located at 10000.12 ∼ 10000.28λ in the z direction and 0 ∼ 13.02λ in the radial direction.

(a) The electron number density vs. the separator position at the time of t = 10000λ/c. (b) The electron energy density vs. the separator position at the time of t = 10000λ/c.
The maximum growth rate of the two-stream instability between the electron bunch and the plasma separator is given by (Rosenbluth et al., 1983)
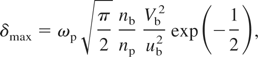
under the condition of
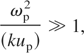
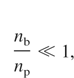
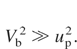
Here, ωp is the beam electron plasma frequency, nb is the beam electron density, np is the plasma separator electron density, Vb is the beam speed, ub is the beam electron thermal speed, up is the plasma separator electron thermal speed, and k is the wave number. In our simulations, the plasma separator parameter values are assumed to be np = 3nc, Vp = 1 eV, and the plasma separator thickness of lp = 2λ (Miyauchi et al., 2004; Sakai et al., 2005). In our case, the plasma separator passage time τele of electrons is about τele = 5.34 fs. The two-stream instability maximum growth rate is δmax = 3.43 × 1012 s−1. This means that the two-stream instability is not so dangerous. The maximum growth rate of the filamentation instability between the beam electrons and the separator electrons is given by Okada and Niu (1980)

at
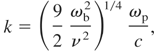
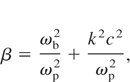
where ν is collision frequency among the plasma separator electrons and ωb is the beam electron plasma frequency. Eq. (15) derived under the conditions of |ζ| > 1,|η| > 1, and ν > δ. Here ζ = (ω + iν)/(kup) and η = ω/(kup), where ω is the complex wave frequency. In this paper, these conditions are fulfilled and δmax = 4.75 × 1012 s−1. The filamentation instability is also not so dangerous. If the plasma separator is not too thick in its width, it serves a stable plasma separator. The electron energy loss by the collisions is estimated by Miyamoto (1989)
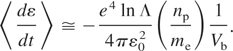
Here dε/dt is the energy loss of the accelerated electron by the collisions with the separator electrons, where e is the electron charge ε0 is the permittivity in vacuum, me is the electron mass and ln Λ is the Coulomb logarithm. In our case, ln Λ ∼ 16. The electron energy loss by the collision is about 6.87 eV in our parameter set. Therefore, the collisional energy loss is negligible.
4. CONCLUSIONS
In this paper, we studied the generation of the high energy and high density attosecond electron bunch by using the TEM (1,0) + TEM (0,1)-mode laser with the plasma separator. When the plasma separator is not employed, the electrons are decelerated at the deceleration phase of the laser, and the density of the electron bunch generated became lower. On the other hand, by setting the plasma separator, after the electrons pass through the plasma separator, the electrons are not decelerated by the laser deceleration phase, and the density of the electron bunch is kept higher. In actual experiments, the plasma separator may be, for example, a thin Al foil. As long as the plasma separator density is overdense and its thickness is sufficiently thin, the plasma separator works (Miyauchi et al., 2004). In our simulations, we employed the specific parameter values for the plasma separator so that the simulation analyses become simple. The simulation results shown that in the case with the plasma separator, the electron number density is ne/ne0 = 16.1, the size of the electron bunch is 454 attosecond (0.17λ) in the z direction, and 12.5λ in the radial direction, the rms emittances of the electron bunch are εx = 7.94 × 10−2π mm mrad and εy = 7.40 × 10−2π mm mrad, the longitudinal momentum spread is 3.66%, and the average energy of the electron bunch is γ ∼ 221. From our parameter study results of the plasma separator position, the allowable plasma separator position shift is ∼±500λ from the optimal position in the z direction.
ACKNOWLEDGMENTS
This work was partly supported by the JSPS (Japan Society for the Promotion of Science) and MEXT (Ministry of Education, Culture, Sports, Science and Technology). We would like to thank Prof. K. Mima, Prof. K. Tachibana, Prof. Yugami, Prof. J. Limpouch, and Prof. S.V. Bulanov for their fruitful discussions on this subject.











