1. INTRODUCTION
Direct vacuum acceleration of charged particle by laser caused intensive attention about 10 years ago (Hussein et al., Reference Hussein, Pato and Kerman1992; Haaland, Reference Haaland1995; Malka et al., 1996; Moore et al., Reference Moore, Knauer and Meyerhofe1995). In this conception, laser can cause charged particle's energy (denoted as relativistic factor Γ) oscillating between a range whose minimum is usually 1 and maximum Γmax is usually proportional to laser strength (or its peak vector potential A max). Detailed relation between Γmax and A max can be referred to the strict three-dimensional (3D) single-body classic dynamics theory (Scheid & Hora, Reference Scheid and Hora1989; Goreslavsky et al., Reference Goreslavsky, Fedorov and Kilpio1995). These investigations confirm the feasibility of laser direct acceleration.
Time-periodic motion within a laser implies that an electron has some probability to escape from the laser with zero or very low energy gain (Scheid & Hora, Reference Scheid and Hora1989; Scully & Zubairy, Reference Scully and Zubairy1991; Kawata et al., Reference Kawata, Maruyama, Watanabe and Takahashi1991; Hussein & Pato,Reference Hussein and Pato1992; Hussein et al., Reference Hussein, Pato and Kerman1992; Bochove et al., Reference Bochove, Moore and Scully1992; Ho & Feng, Reference Ho and Feng1994; Rau et al., Reference Rau, Tajima and Hojo1997). The energy gain distributes, with different probabilities, over a range from 0 to Γmax − 1. Although in the case of higher laser peak-intensity A max2, the effect of light pressure can exert a static force on electron and hence enhance its Γmin from 1 to a higher value proportional to A max2 (Brown & Kibble, Reference Brown and Kibble1964; Sarachik & Schappert, Reference Sarachik and Schappert1970; Steinhauer & Kimura, Reference Steinhauer and Kimura1992; Hauser et al., 1994; Haaland, Reference Haaland1995; Sprangle et al., Reference Sprangle, Esarey, Krall and Ting1996; Hartemann et al., Reference Hartemann, Fochs, Le Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995; Reference Hartemann, Van Meter, Troha, Landahl, Luhmann, Baldis, Gupta and Kerman1998; Troha et al., Reference Troha, Van Meter, Landahl, Alvis, Unterberg, Li, Luhmann, Kerman and Hartemann1999; Esarey et al., Reference Esarey, Sprangle and Krall1995; Reference Esarey, Sprangle, Krall and Ting1996; Ho et al., Reference Ho, Wang, Feng, Scheid and Hora1996; Goreslavsky et al., Reference Goreslavsky, Fedorov and Kilpio1995), this demands the electromagnetic energy carried by the laser to be large enough. In contrast, a static electric field can drive an electron to do a time-monotonic motion and hence always increase electron's energy. Therefore, the energy gain within a static electric field is proportional to the time an electron takes to travel within the field.
Increasing laser peak-intensity A max2 is the most common route of optimizing the acceleration. It is also worthy of trying another route: depressing the probability of lower energy gain. Obviously, although only a stimulus (i.e., the laser) can achieve this goal because of the effect of light pressure (or ponderomotive force), the laser is required to be powerful enough. Here, we study the acceleration by a compound field setup which contains a linear polarized laser beam and a static (or DC) electric field along the direction of laser magnetic field. Our motive for using such a compound field setup is to depress, with the help of the static electric field, the probability of lower energy gain. Clearly, if the probability of lower energy gain is limited greatly, the quality or the efficiency of the acceleration will be warranted even though A max2 is not too high.
This also forces us to consider how to optimize the acceleration. Concentrating all electromagnetic energy in a stimulus or sharing the electromagnetic energy between two stimuli? A mixture of the time-periodic motion and the time-monotonic one is obviously desirable to the acceleration. Especially, the contribution from the time-monotonic motion increases with respect to the time. If only a laser is applied, an electron will do mainly the time-periodic motion even though the light pressure can casue little time-monotonic one. Therefore, sharing the electromagnetic energy between the laser and the static electric field is estimated to be more favorable to the acceleration than concentrating it in the laser. Stricter conclusion should be based on the following detailed theory and calculations.
On the other hand, such a mixed motion is also advantageous than a pure time-monotonic motion driven by a static electric field. If there is only a stimulus (static electric field), the motion vertical to the electric field, as shown latter, will have no contribution to energy gain. This is the reason for why our interest is focused on such a mixed motion.
2. THEORY AND RESULTS
Now we study the single-body dynamics of charged particle in a compound field: a DC electric field E y = G (where G is a constant) and a laser (E x = E m sin (kz–ωt), B y = B m sin (kz−ωt)). Here, the laser propagates in vacuum and hence meets two relations: E m = cB m and ω = kc. Dimensionless 3D relativistic Newton equation set (RNEs) read
where ![]() ${\rm \lambda } = 2{\rm \pi }{c \over {\rm \omega} }$,
${\rm \lambda } = 2{\rm \pi }{c \over {\rm \omega} }$, ![]() ${\rm \theta} = {{z - ct} \over {\rm \lambda}}\, \ast\, 2{\rm \pi }$,
${\rm \theta} = {{z - ct} \over {\rm \lambda}}\, \ast\, 2{\rm \pi }$, ![]() $s = {\rm \omega} t$,
$s = {\rm \omega} t$, ![]() ${\rm \omega} _B = {{eB} \over {m_e }}$ and
${\rm \omega} _B = {{eB} \over {m_e }}$ and ![]() ${\rm \omega} _G = {{eG} \over {m_e c}}$. Eqs.(1), (3) will yield
${\rm \omega} _G = {{eG} \over {m_e c}}$. Eqs.(1), (3) will yield
Here, the value of constant in Eq. (5) is determined by the initial condition (at t = 0, there are ![]() $d_s {x \over {\rm \lambda} } = 0$, Γ = 1 and θ = 0), and hence Eq.(5) can be re-written as
$d_s {x \over {\rm \lambda} } = 0$, Γ = 1 and θ = 0), and hence Eq.(5) can be re-written as
Due to the definition ![]() $1/\Gamma = \sqrt {1 - \mathop {\left({d_s {x \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s {y \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s {z \over {\rm \lambda} }} \right)}\nolimits^2 } $, Eqs.(4), (6) will yield
$1/\Gamma = \sqrt {1 - \mathop {\left({d_s {x \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s {y \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s {z \over {\rm \lambda} }} \right)}\nolimits^2 } $, Eqs.(4), (6) will yield
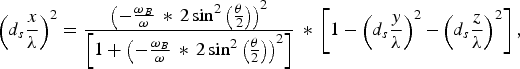 $$\mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \over {\left[{1 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \right]}} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$
$$\mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \over {\left[{1 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \right]}} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$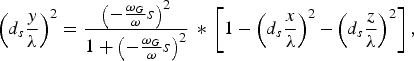 $$\mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$
$$\mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$and hence
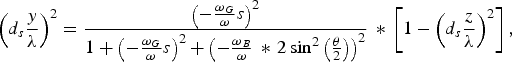 $$\mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$
$$\mathop {\left({d_s \displaystyle{y \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right]\comma \;$$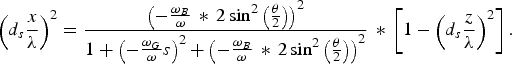 $$\mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega}} \,\ast\, 2\sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right].$$
$$\mathop {\left({d_s \displaystyle{x \over {\rm \lambda} }} \right)}\nolimits^2 = \displaystyle{{\mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2 \sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 } \over {1 + \mathop {\left({ - {{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - {{{\rm \omega} _B } \over {\rm \omega}} \,\ast\, 2\sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }} \,\ast\, \left[{1 - \mathop {\left({d_s \displaystyle{z \over {\rm \lambda} }} \right)}\nolimits^2 } \right].$$For convenience in expressing formulas, we introduce symbols
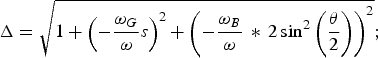 $$\Delta = \sqrt {1 + \mathop {\left({ - \displaystyle{{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2\sin^2 \left({\displaystyle{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }\semicolon \;$$
$$\Delta = \sqrt {1 + \mathop {\left({ - \displaystyle{{{\rm \omega} _G } \over {\rm \omega} }s} \right)}\nolimits^2 + \mathop {\left({ - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2\sin^2 \left({\displaystyle{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }\semicolon \;$$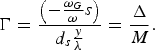 $$\Gamma = \displaystyle{{\left({ - {\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}s} \right)} \over {d_s {\textstyle{y \over {\rm \lambda} }}}} = \displaystyle{\Delta \over M}.$$
$$\Gamma = \displaystyle{{\left({ - {\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}s} \right)} \over {d_s {\textstyle{y \over {\rm \lambda} }}}} = \displaystyle{\Delta \over M}.$$Thus, Eq.(2) is re-written as
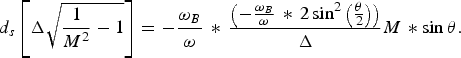 $$d_s \left[{\Delta \sqrt {\displaystyle{1 \over {M^2 }} - 1} } \right]= - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, \displaystyle{{\left({ - {{{\rm \omega} _B } \over {\rm \omega}} \,\ast\, 2\sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)} \over \Delta }{M} \,\ast \sin{\rm \theta}.$$
$$d_s \left[{\Delta \sqrt {\displaystyle{1 \over {M^2 }} - 1} } \right]= - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, \displaystyle{{\left({ - {{{\rm \omega} _B } \over {\rm \omega}} \,\ast\, 2\sin^2 \left({{{\rm \theta} \over 2}} \right)} \right)} \over \Delta }{M} \,\ast \sin{\rm \theta}.$$From definitions Eqs.(11), (12), we have
and re-write Eq.(14) as
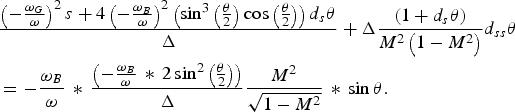 $$\eqalign{&\displaystyle{\left( - {{\rm \omega}_G \over {\rm \omega}} \right)^2 s + 4 \left(- {{\rm \omega}_B \over {\rm \omega}} \right)^2 \left(\sin^3 \left({{\rm \theta} \over 2} \right) \cos \left({{\rm \theta} \over 2} \right) \right) d_s {\rm \theta} \over \Delta} + \Delta \displaystyle{\left(1 + d_s {\rm \theta} \right) \over M^2 \left(1 - M^2 \right)} d_{ss} {\rm \theta} \cr &= - \displaystyle{{\rm \omega}_B \over {\rm \omega}} \,\ast\, \displaystyle{\left( - {{\rm \omega}_B \over {\rm \omega}} \, \ast \, 2 \sin^2 \left({{\rm \theta} \over 2} \right) \right) \over \Delta} \displaystyle{M^2 \over \sqrt{1 - M^2}} \,\ast \, \sin {\rm \theta}.}$$
$$\eqalign{&\displaystyle{\left( - {{\rm \omega}_G \over {\rm \omega}} \right)^2 s + 4 \left(- {{\rm \omega}_B \over {\rm \omega}} \right)^2 \left(\sin^3 \left({{\rm \theta} \over 2} \right) \cos \left({{\rm \theta} \over 2} \right) \right) d_s {\rm \theta} \over \Delta} + \Delta \displaystyle{\left(1 + d_s {\rm \theta} \right) \over M^2 \left(1 - M^2 \right)} d_{ss} {\rm \theta} \cr &= - \displaystyle{{\rm \omega}_B \over {\rm \omega}} \,\ast\, \displaystyle{\left( - {{\rm \omega}_B \over {\rm \omega}} \, \ast \, 2 \sin^2 \left({{\rm \theta} \over 2} \right) \right) \over \Delta} \displaystyle{M^2 \over \sqrt{1 - M^2}} \,\ast \, \sin {\rm \theta}.}$$ We denote the direction of electric field as ![]() $\overrightarrow{e_\parallel} $ and the direction vertical to electric field as
$\overrightarrow{e_\parallel} $ and the direction vertical to electric field as ![]() $\overrightarrow {e_ \bot } $. Clearly, the contribution from the motion of charged particle along
$\overrightarrow {e_ \bot } $. Clearly, the contribution from the motion of charged particle along ![]() $\overrightarrow {e_ \bot } $ to Γmax is not clear enough. The formula d t Γ = E · υ reflects that the dependence of Γ on
$\overrightarrow {e_ \bot } $ to Γmax is not clear enough. The formula d t Γ = E · υ reflects that the dependence of Γ on ![]() ${\rm \upsilon} _\parallel $. Because Γ depends on both
${\rm \upsilon} _\parallel $. Because Γ depends on both ![]() ${\rm \upsilon} _\parallel $ and
${\rm \upsilon} _\parallel $ and ![]() ${\rm \upsilon} _ \bot $, this formula reflects the relation between Γ and
${\rm \upsilon} _ \bot $, this formula reflects the relation between Γ and ![]() ${\rm \upsilon} _\parallel $ when
${\rm \upsilon} _\parallel $ when ![]() ${\rm \upsilon} _ \bot $ is given and hence should be denoted more strictly as
${\rm \upsilon} _ \bot $ is given and hence should be denoted more strictly as ![]() $d_t \Gamma \vert _{d_t {\rm \upsilon} _ \bot = 0} = E \cdot {\rm \upsilon} $. Namely, we can always obtain d t Γ = E · υ from RNEs if
$d_t \Gamma \vert _{d_t {\rm \upsilon} _ \bot = 0} = E \cdot {\rm \upsilon} $. Namely, we can always obtain d t Γ = E · υ from RNEs if ![]() $d_t {\rm \upsilon} _ \bot = 0$. Clearly, once
$d_t {\rm \upsilon} _ \bot = 0$. Clearly, once ![]() $d_t {\rm \upsilon} _ \bot = 0$ cannot be warranted, Γ (t), which should be equal to
$d_t {\rm \upsilon} _ \bot = 0$ cannot be warranted, Γ (t), which should be equal to ![]() $\Gamma \left(0 \right)+ \vint d_t \Gamma \vert _{d_t {\rm \upsilon} _ \bot = 0} dt + \vint d_t \Gamma \vert _{d_t {\rm \upsilon} _\parallel = 0} dt$, might be different from Γ ( 0 ) + ∫ E · υ dt.
$\Gamma \left(0 \right)+ \vint d_t \Gamma \vert _{d_t {\rm \upsilon} _ \bot = 0} dt + \vint d_t \Gamma \vert _{d_t {\rm \upsilon} _\parallel = 0} dt$, might be different from Γ ( 0 ) + ∫ E · υ dt.
The 3D RNEs is ultimately reduced to Eq. (17), a second-order differential equation of ![]() $z = \vint {\rm \upsilon} _ \bot dt$. All related quantities can be calculated from this equation. In this compound field setup, due to the DC electric field, the motion of a charged particle is no longer periodic even though the laser is a periodic stimulus. As shown in Figure 1, Γ rises with respect to t in an oscillatory manner. If no DC electric field is applied, i.e.,
$z = \vint {\rm \upsilon} _ \bot dt$. All related quantities can be calculated from this equation. In this compound field setup, due to the DC electric field, the motion of a charged particle is no longer periodic even though the laser is a periodic stimulus. As shown in Figure 1, Γ rises with respect to t in an oscillatory manner. If no DC electric field is applied, i.e., ![]() ${{{\rm \omega} _G } \over {\rm \omega} } = 0$, Γ will periodically oscillate between 1 and a time-independent Γmax, and Γmax −1 is proportional to
${{{\rm \omega} _G } \over {\rm \omega} } = 0$, Γ will periodically oscillate between 1 and a time-independent Γmax, and Γmax −1 is proportional to ![]() ${{{\rm \omega} _B } \over {\rm \omega} } = {{eA_{\rm max} } \over {mc^2 }}$ (Scheid & Hora, Reference Scheid and Hora1989; Goreslavsky et al., Reference Goreslavsky, Fedorov and Kilpio1995; Lin et al., Reference Lin, Liu, Du and Wang2013). If
${{{\rm \omega} _B } \over {\rm \omega} } = {{eA_{\rm max} } \over {mc^2 }}$ (Scheid & Hora, Reference Scheid and Hora1989; Goreslavsky et al., Reference Goreslavsky, Fedorov and Kilpio1995; Lin et al., Reference Lin, Liu, Du and Wang2013). If ![]() ${{{\rm \omega} _G } \over {\rm \omega} } \ll {{{\rm \omega} _B } \over {\rm \omega} }$, Γ will do nearly periodical oscillation (see green dotted line in the down panel of Fig. 1). Likewise, if no laser is applied, i.e.,
${{{\rm \omega} _G } \over {\rm \omega} } \ll {{{\rm \omega} _B } \over {\rm \omega} }$, Γ will do nearly periodical oscillation (see green dotted line in the down panel of Fig. 1). Likewise, if no laser is applied, i.e., ![]() ${{{\rm \omega} _B } \over {\rm \omega}} = 0$, Γ will monotonically rises with respect to t (see black solid line in Fig. 2). Clearly, the oscillatory rising, which is aperiodic, reflects combined effect of the laser and the DC electric field.
${{{\rm \omega} _B } \over {\rm \omega}} = 0$, Γ will monotonically rises with respect to t (see black solid line in Fig. 2). Clearly, the oscillatory rising, which is aperiodic, reflects combined effect of the laser and the DC electric field.

Fig. 1. Example of time history of Γ.

Fig. 2. Example of time history of Γ.
It is worthy to note that under the same energy density of the stimulus, aperiodic motion favors higher Γmax than periodic one. Because the electromagnetic energy density is ![]() ${^\sim} \left({{\rm \omega} _B \over {\rm \omega}} \right)^2 $, the energy density of a laser beam of
${^\sim} \left({{\rm \omega} _B \over {\rm \omega}} \right)^2 $, the energy density of a laser beam of ![]() ${{{\rm \omega} _B } \over {\rm \omega}}={\sqrt 2} a$ will be equal to the summation of those of two laser beams of
${{{\rm \omega} _B } \over {\rm \omega}}={\sqrt 2} a$ will be equal to the summation of those of two laser beams of ![]() ${{{\rm \omega} _B } \over {\rm \omega} }=a$. As shown in Figure 1, for nearly same energy density,
${{{\rm \omega} _B } \over {\rm \omega} }=a$. As shown in Figure 1, for nearly same energy density, ![]() $\left({{\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}\comma \; {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}} \right)=\left({0.01\comma \; 0.01} \right)$ is more favorable to high Γ than
$\left({{\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}\comma \; {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}} \right)=\left({0.01\comma \; 0.01} \right)$ is more favorable to high Γ than ![]() $\left({{\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}\comma \; {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}} \right)=\left({0.0001\comma \; 0.015} \right)$ (here because of
$\left({{\textstyle{{{\rm \omega} _G } \over {\rm \omega} }}\comma \; {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}} \right)=\left({0.0001\comma \; 0.015} \right)$ (here because of ![]() ${\sqrt 2}=1.414 ^{\sim} 1.5$, we approximate 0.015 as
${\sqrt 2}=1.414 ^{\sim} 1.5$, we approximate 0.015 as ![]() $0.01\, \ast\, {\sqrt 2} $. ). More interest, high Γmax is mainly contributed by high
$0.01\, \ast\, {\sqrt 2} $. ). More interest, high Γmax is mainly contributed by high ![]() ${\rm \upsilon} _ \bot ^2 $ instead of
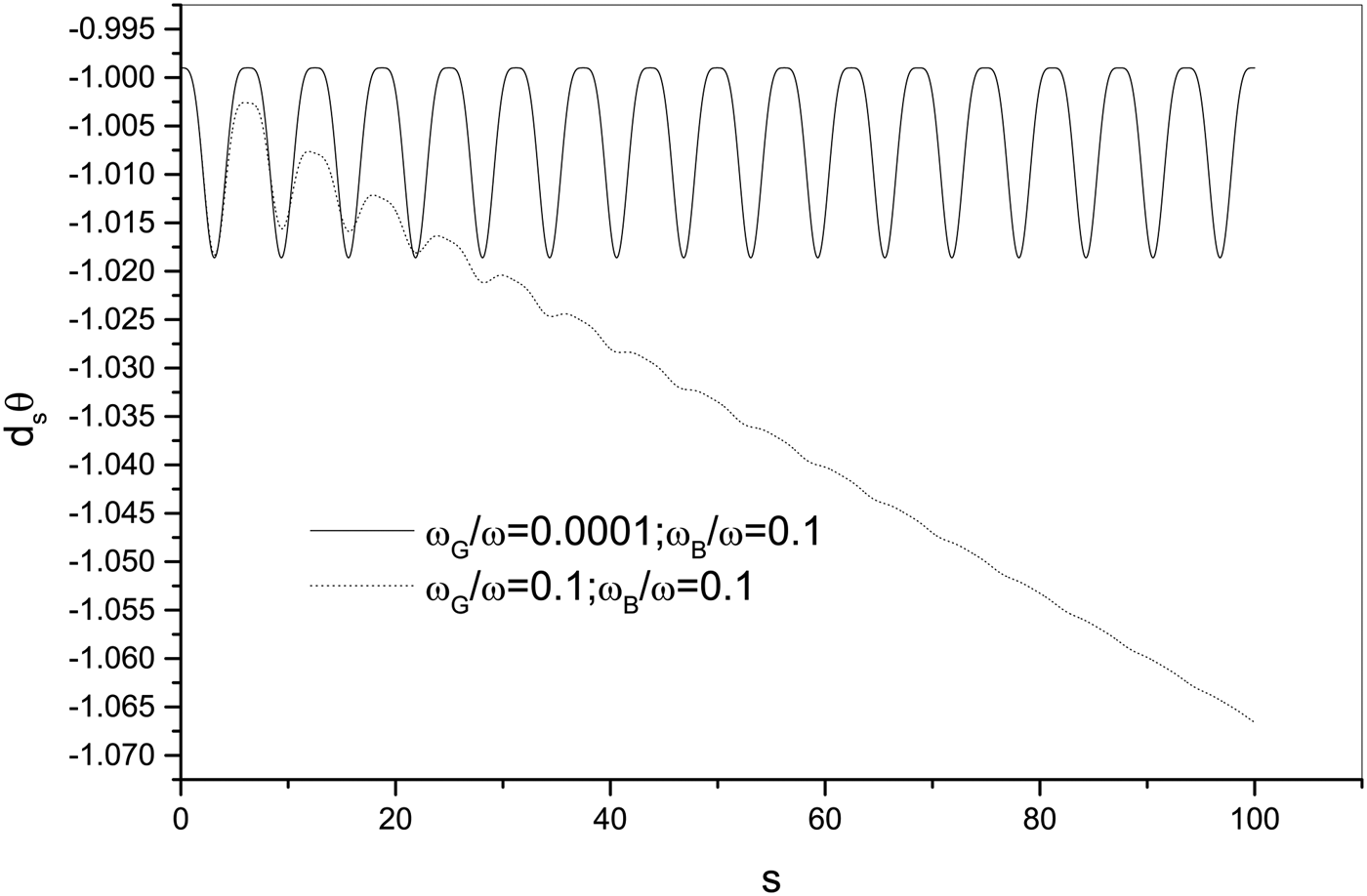
${\rm \upsilon} _ \bot ^2 $ instead of ![]() ${\rm \upsilon} _\parallel ^2 $. As shown in Figure 3, d s θ, which is just dimensionless
${\rm \upsilon} _\parallel ^2 $. As shown in Figure 3, d s θ, which is just dimensionless ![]() ${\rm \upsilon} _ \bot $ subtracting 1, obviously differs from −1. This implies that
${\rm \upsilon} _ \bot $ subtracting 1, obviously differs from −1. This implies that ![]() ${\rm \upsilon} _ \bot $ obviously differs from 0 and hence have marked contribution to high Γmax-value. Here, we should also note that if
${\rm \upsilon} _ \bot $ obviously differs from 0 and hence have marked contribution to high Γmax-value. Here, we should also note that if ![]() ${{{\rm \omega} _B } \over {\rm \omega} } = 0$, there will be always
${{{\rm \omega} _B } \over {\rm \omega} } = 0$, there will be always ![]() ${\rm \upsilon} _ \bot = 0$. Namely, the laser is necessary for ensuring
${\rm \upsilon} _ \bot = 0$. Namely, the laser is necessary for ensuring ![]() ${\rm \upsilon} _ \bot \ne 0$.
${\rm \upsilon} _ \bot \ne 0$.

Fig. 3. Example of time history of d sθ.
According to strict theories (Scheid & Hora, Reference Scheid and Hora1989; Goreslavsky et al., Reference Goreslavsky, Fedorov and Kilpio1995), the laser enables particle's velocity to be periodic. The periodicity limits Γ to be ![]() $\les \Gamma_{\rm max}$ whose value is determined by laser strength E max. Usually people choose to increase Γmax by enhancing E max under same setup (i.e., a single laser beam). Above results have shown that trying different setups might be more effective to find better acceleration scheme. The compound field setup described above has clearly illustrated a typical example of better acceleration. In short, how to harness the motion vertical to the electric field is a worthy issue for ensuring higher Γmax. Because of the formula d t Γ = E · υ, the importance of
$\les \Gamma_{\rm max}$ whose value is determined by laser strength E max. Usually people choose to increase Γmax by enhancing E max under same setup (i.e., a single laser beam). Above results have shown that trying different setups might be more effective to find better acceleration scheme. The compound field setup described above has clearly illustrated a typical example of better acceleration. In short, how to harness the motion vertical to the electric field is a worthy issue for ensuring higher Γmax. Because of the formula d t Γ = E · υ, the importance of ![]() ${\rm \upsilon} _ \bot ^2 $ to higher Γmax has been underestimated greatly.
${\rm \upsilon} _ \bot ^2 $ to higher Γmax has been underestimated greatly.
A simple estimation can illustrate the effect of ![]() ${\rm \upsilon} _ \bot ^2 $ to Γmax. According to Eq.(10), if
${\rm \upsilon} _ \bot ^2 $ to Γmax. According to Eq.(10), if ![]() ${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$ and
${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$ and ![]() ${\rm \upsilon} _ \bot ^2 \equiv 0$ exist, there will be
${\rm \upsilon} _ \bot ^2 \equiv 0$ exist, there will be ![]() $\Gamma = 1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 } = \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } $, which can also be derived from
$\Gamma = 1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 } = \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } $, which can also be derived from ![]() $d_s \left[{1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 } } \right]= {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}\sin{\rm \theta} \,\ast\, {d_s} {\textstyle{x \over {\rm \lambda} }}$. In contrast, if
$d_s \left[{1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 } } \right]= {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }}\sin{\rm \theta} \,\ast\, {d_s} {\textstyle{x \over {\rm \lambda} }}$. In contrast, if ![]() ${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$ exists but
${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$ exists but ![]() ${\rm \upsilon} _ \bot ^2 \equiv 0$ not, Eq.(10) will yield
${\rm \upsilon} _ \bot ^2 \equiv 0$ not, Eq.(10) will yield ![]() $\Gamma = 1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 - \mathop {\left({d_s {\textstyle{z \over {\rm \lambda} }}} \right)}\nolimits^2 } = \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } /$
$\Gamma = 1/\sqrt {1 - \mathop {\left({d_s {\textstyle{x \over {\rm \lambda} }}} \right)}\nolimits^2 - \mathop {\left({d_s {\textstyle{z \over {\rm \lambda} }}} \right)}\nolimits^2 } = \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } /$![]() ${\sqrt {1 - \mathop {\left({d_s {\textstyle{z \over {\rm \lambda} }}} \right)}\nolimits^2 } \,\gt\,} \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } $. The > well illustrates the underestimation of Γ if
${\sqrt {1 - \mathop {\left({d_s {\textstyle{z \over {\rm \lambda} }}} \right)}\nolimits^2 } \,\gt\,} \sqrt {1 + \mathop {\left({ - {\textstyle{{{\rm \omega} _B } \over {\rm \omega} }} \,\ast\, 2\sin^2 \left({{\textstyle{{\rm \theta} \over 2}}} \right)} \right)}\nolimits^2 } $. The > well illustrates the underestimation of Γ if ![]() ${\rm \upsilon} _ \bot ^2 \equiv 0$ is taken for granted.
${\rm \upsilon} _ \bot ^2 \equiv 0$ is taken for granted.
Moreover, for ![]() ${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$, there will be
${\textstyle{{{\rm \omega} _G } \over {\rm \omega} }} = 0$, there will be ![]() $d_s {\textstyle{y \over {\rm \lambda} }} \equiv 0$ and
$d_s {\textstyle{y \over {\rm \lambda} }} \equiv 0$ and
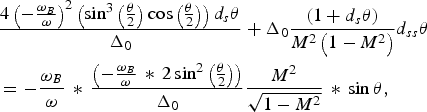 $$\eqalign{&\displaystyle{4 \left( - {{\rm \omega}_B \over {\rm \omega}} \right)^2 \left(\sin^3 \left({{\rm \theta} \over 2} \right) \cos \left({{\rm \theta} \over 2} \right) \right)d_s {\rm \theta} \over \Delta_0} + \Delta_0 \displaystyle{\left(1 + d_s {\rm \theta} \right) \over M^2 \left(1 - M^2 \right)} d_{ss} {\rm \theta} \cr & = - \displaystyle{{\rm \omega}_B \over {\rm \omega}} \, \ast \, \displaystyle{\left( - {{\rm \omega}_B \over {\rm \omega}} \, \ast \, 2 \sin^2 \left({{\rm \theta} \over 2} \right) \right) \over \Delta_0} \displaystyle{M^2 \over \sqrt{1 - M^2}} \, \ast \, \sin {\rm \theta} \comma \; }$$
$$\eqalign{&\displaystyle{4 \left( - {{\rm \omega}_B \over {\rm \omega}} \right)^2 \left(\sin^3 \left({{\rm \theta} \over 2} \right) \cos \left({{\rm \theta} \over 2} \right) \right)d_s {\rm \theta} \over \Delta_0} + \Delta_0 \displaystyle{\left(1 + d_s {\rm \theta} \right) \over M^2 \left(1 - M^2 \right)} d_{ss} {\rm \theta} \cr & = - \displaystyle{{\rm \omega}_B \over {\rm \omega}} \, \ast \, \displaystyle{\left( - {{\rm \omega}_B \over {\rm \omega}} \, \ast \, 2 \sin^2 \left({{\rm \theta} \over 2} \right) \right) \over \Delta_0} \displaystyle{M^2 \over \sqrt{1 - M^2}} \, \ast \, \sin {\rm \theta} \comma \; }$$where
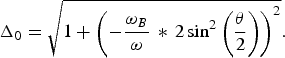 $$\Delta _0=\sqrt {1+\mathop {\left({ - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2\sin^2 \left({\displaystyle{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }.$$
$$\Delta _0=\sqrt {1+\mathop {\left({ - \displaystyle{{{\rm \omega} _B } \over {\rm \omega} } \,\ast\, 2\sin^2 \left({\displaystyle{{\rm \theta} \over 2}} \right)} \right)}\nolimits^2 }.$$A straightforward deduction can confirm that Eq.(18) corresponds to a first integral and hence has periodic solutions. In contrast, Eq.(17) does not have periodic solutions.
People have been aware that the combination filed can lead to significant acceleration. For example, Yin et al., (Reference Yin, Albright, Heglich and Fernández2006) and Flippo et al., (Reference Flippo, Hegelich and Albright2007) attributed high-energy ions appearing in the interaction of intense laser with thin solid target to the acceleration by the combination of a transverse field (i.e., laser) and a longitudinal electric field (i.e., sheath field). In the cases they studied, the laser is “actively” applied and the longitudinal electric field is “passively” generated. Moreover, the longitudinal electric field is time-dependent and its direction is fixed to be along the propagation direction of the laser (and hence vertical to that of laser magnetic field). In contrast, the case we studied is of more flexible arrangement of the fields. Both the transverse field and the longitudinal one are “actively” applied, the longitudinal field is time-independent and flexible adjustment on its direction is available. Such a flexible arrangement enables us to make a full utilization of the merit of the combination acceleration.
3. SUMMARY
For higher efficiency, we extend investigation on laser direction vacuum acceleration to the cases of multiple stimuli. The advantage of multiple stimuli over single stimulus is confirmed by strict theory and numerical results. Especially, the importance of the motion vertical to the direction of electric field to the acceleration is reflected by strict analysis and numerical results. This implies that how to make a full utilization of ![]() ${\rm \upsilon} _ \bot ^2 $ is essential to warrant high-efficiency acceleration.
${\rm \upsilon} _ \bot ^2 $ is essential to warrant high-efficiency acceleration.
ACKNOWLEDGEMENT
This work is supported by National Science Fund grant no 11374318 and 11335013.