1. INTRODUCTION: IMPOSSIBLE MISSIONS
For scientific purposes, there are missions through the solar system that would be desirable to accomplish, but they are essentially impossible using chemical or nuclear thermal rockets. One example is a solar impact mission, which requires the rocket to cancel out the orbital velocity of the earth, so that the vehicle can drop directly into the sun. This requires a mission characteristic velocity of 35 km/s, which is presently obtained by an out-of-the-way swingby around Jupiter, 5 AU, and many years in the wrong direction. Another is a mission to the rings deep down in the gravity well of Saturn. This requires a mission characteristic velocity of 48 km/s.
There are simpler missions near earth that are nearly impossible using chemical rockets. One is the simple maneuver of rapidly reversing the orbital direction. This maneuver requires canceling the initial orbital velocity and then building it up again in the opposite direction. Since earth orbital velocity is 7.7 km/s, the total mission characteristic velocity of the reverse orbit maneuver is 15.5 km/s. If it is desired to return to the initial orbit, to dock at an orbiting space station base, the process must be repeated with a total mission characteristic velocity of 31 km/s (Forward, 1985a, 1985b).
The mass ratios required for each type of rocket system to carry out each of these missions can be calculated from the rocket equation
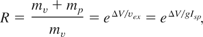
in terms of requested velocity variations ΔV, where mv is the mass of the empty vehicle (including payload) delivered to destination, and mp denotes the propellant mass exhausted at velocity Vex or specific impulse Isp, while g = 9.8 m/s2 is the gravitation constant at the earth surface.
The mass ratios discussed above are listed in Table 1. As can be seen, all of these missions require high mass ratios, with the more difficult ones requiring such a large mass ratio that it is difficult, if not impossible, to imagine how one might build a vehicle to accomplish such missions using chemical or nuclear thermal rockets. All of those missions could be performed by fusion or antimatter rockets with a mass ratio of 5:1 or less.
Mass ratios for difficult missions

In this connection, it is appropriate to recall that nuclear (fission) thermal propulsion could provide only a factor of two improvements upon standard cryogenic propulsion (SCP).
Viewing matter annihilation at the upper limit of what thermonuclear propulsion can achieve, in our analysis, we will look at the various approaches affordable through fusion in a broad sense for long distance journeys in the solar system. Fusion thus appears as the only option that potentially achieves the most important regime for solar system travel.
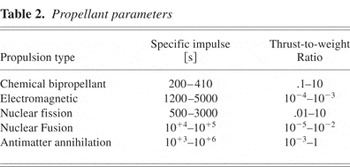
Exhaust velocities of 105 to 106 m/s at thrust-to-weight ratio of 10−3. Such levels of performance allow for both human and efficient cargo transport. Specific parameters qualifying various propellants are detailed on Table 2.
Propellant parameters
It is interesting to note that 100 mg of antimatter is equivalent to the space shuttle propulsive energy.
2. BASIC CONCEPTS
The potential benefits of space propulsion by nuclear fusion will be briefly shown here by a simple analysis.
Roughly, to accelerate a mass Mw to a speed vc in a time τ requires a thrust power Pw given by
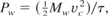
from which we define the characteristic velocity vc by
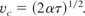
Here α = Pw /Mw is the specific power, defined in relation to the mass Mw of the propulsion system. The corresponding flight distance L is roughly related to the flight time by
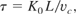
where K0 is a constant of order unity. Combining Eqs. (2) and (4) gives, with appropriate conversions of the units, yields the following
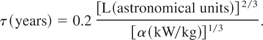
Here, K0 = 3 provide a reasonable fit for the orbit calculations in the literature.
The payload delivered is the other key figure of merit besides the flight time in assessing rocket performance. The payload mass (including rocket structure) can be related to the initial rocket mass, including propellant by the well-know rocket equation, Eq. (1).
Optimum payload management typically corresponds to
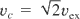
, with a final velocity near the characteristic velocity. Thus, to reach 1 AU in 1 year with a 0.1 payload fraction at a specific power of 1 kW/kg requires an exhaust velocity on the order of 105 m/s, or a specific impulse of about 104 s. These parameters are consistent with magnetic fusion dipole fusion rocket (Teller et al., 1992; Hora, 2004), but are beyond the capabilities of either nuclear fission thermal systems, in which reactors heat the propellant directly (high specific power, but lower specific impulse), or nuclear fission electric systems, in which reactors supply electricity to ion accelerators (high specific impulse, but low power).
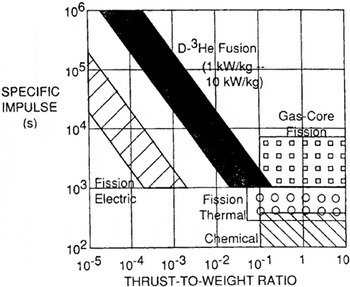
Figure 1 plots Eq. (5) for various high specific impulse systems and illustrates the potential of fusion propulsion. All values plotted in Figure 1 correspond to vex < 106 ms−1, well within the capability of fusion rockets. In a fusion rocket, vex can be readily adjusted up to vex ≅ 107 ms−1, or a specific impulse of 106 s, corresponding to direct exhaust of the hot fuel as propellant, and even faster speeds could be achieved by selective exhaust of certain reaction products. However, as already noted, specific power rather than specific impulse is the primary constraint.

Mission distance L versus flight time τ for different ratios of thrust power to mass of propulsion system.
Specific powers in the range of 1 kW/kg, already an order of magnitude better than nuclear fission electric systems, appear quite feasible, and we will discuss one such system, the dipole. As one can see from the figure, at a few kW/kg specific powers, interplanetary trips would require only months, and the Tau mission (1000 AU) would require only 10 to 20 years.
3. MAGNETIC FUSION ENERGY (MFE)
When more than a few hundred kilowatts of steady-state power are required for space applications, the only feasible choices appear to be nuclear fission or nuclear fusion. Space application places different and stringent constraints on the choice of fusion reactions and fusion confinement systems than do ground-based electric utility applications. In space, the dominant constraint is a minimum mass per unit of power output; for ground-based utilities, the cost of electricity is the dominant constraint. For seeable applications of fusion reactors to space-related power and propulsion systems appear to require thermal power levels ranging from 10 MW up to 1 GW. There appears to be no mission for the GW reactors currently of interest to the electrical utilities. Desirable characteristics of fusion reactors for space include avoidance of tritium-fueled reactions; and operation that is as nearly aneutronic as possible; a steady-state operation; an operation at high beta, with a plasma stability index greater than β = 0.20; the use of direct conversion or direct production of thrust to minimize the power flows that must be handled by heavy energy conversion equipment; and a value of the system-specific mass below α = 5 kg/KW (electric), to be competitive with fission systems for space applications. Only the deuterium-tritium (D-T) reaction appears feasible for magnetic fusion reactors having large recirculating power flows; for reactors with little recirculating power, the best all-around fusion reaction for space applications appears to be D-3He.
3.1. D-3He
A preliminary assessment of propulsion with D-3He fusion is given in Figure 2, where specific impulse is evaluated for several propellants.
Comparison of DHe3 fusion with chemical, nuclear thermal, and nuclear electric propulsion systems.
3.2. Advantages of D-3He magnetic fusion for space applications
- No radioactive materials are present at launch, and only low-level radioactivity remains after operation.
- Conceptual designs project higher specific power values (1–10 kW-thrust/kg) for fusion than for nuclear-electric or solar-electric propulsion.
- Fusion gives high, flexible specific impulses (exhaust velocities), enabling efficient long-range transportation.
- D-3He produces net energy and is available throughout the solar system.
- D-3He fuel provides an extremely high energy density.
Among systems implementing thermonuclear fusion through magnetic confinement, the tokamak architecture is far ahead by virtue of superior performance in the laboratory. A typical propulsion scenario using the given toroidal geometry is depicted in Figure 3.

Major subsystems of toroidal fusion rocket propulsion system (Roth, 1989).
The projected specific powers for selected designs appear in the Table 3; widely varying assumptions and levels of optimism have gone into the conceptual designs and the resulting specific powers.
AIMStar 50 year Mission to 10000 AU

4. INERTIAL FUSION ENERGY (IFE)
Inertial fusion is a topic of intense research worldwide (Nuckolls et al., 1972; Hora, 2004; Kilkenny et al., 2005; Koresheva et al., 2005; Leon et al., 2006; Li et al., 2004; Perlado et al., 2005). The possibility of igniting thermonuclear micro-explosions with pulsed laser beams was first proposed by Basov and Krokhin (1964). The idea of using for the same purpose, intense beams of charged heavy particles, accelerated in conventional linear high energy particle accelerators, was proposed at about the same time (Winterberg, 1964). Corresponding heavy ion drivers used in a so-called direct drive compression of the pellet containing DT fuel, and the problems associated with particle beams penetrating plasma (Deutsch et al., 1989; Deutsch, 2004), have been extensively reviewed (Deutsch, 1986).
The suggestion of a rocket motor to be driven by a chain of explosions was first proposed by Ganswindt (1899). Following the discovery of nuclear explosives by Hahn and Strassmann (1939), this idea was revived by Everett and Ulam (1950), and a feasibility study under the name Project Orion was made. In this particular concept, it was intended to explode a chain of small fission bombs behind a pusher plate, which prior to each explosion, would have to be covered by a layer of liquid, for example, water to protect it from the intense heat generated by the fission explosive. In this way, a large thrust at a high specific impulse would be imparted onto the pusher plate, and hence the spacecraft. The limitation of such a propulsion system is determined by the maximum permissible temperature of ∼ 105 °K, which the evaporating liquid is permitted to attain without destroying the pusher plate. The great technical problem of such a system is the critical mass of a fission chain reaction, making it difficult to miniaturize a fission explosion. The explosive power of the fission bombs is always very large and the proposed device is therefore at the limit of technical feasibility. It is also obvious that there is no improvement if instead of fission explosives thermonuclear explosives, to be triggered themselves with fission explosives, are being used. If however, the fission trigger can be replaced by some other means permitting the ignition of thermonuclear micro-explosions, the situation is drastically changed for the better.
Winterberg (1968) proposed to ignite micro-explosions through pulse power techniques (Winterberg, 2006), producing intense pulsed beams of either relativistic electrons or space charge neutralized ions, which have the best chance to be successfully developed for a mobile system.
Such a proposal going back to 1968, received very recently a novel boost with the developed of the fast ignition concept (FIC). FIC has been initially proposed by Tabak et al. (1994), and it has been recently reviewed by Deutsch (2003). FIC elaborates on the recently proposed ultraintense and chirped lasers, which can produce highly directed and ultraintense beams of relativistic electrons in the MeV energy range. Moreover, it is also possible to convert the latter into fully neutralized proton beams in the 1–70 MeV energy range.
The emphasis on particle trigger is largely motivated by the fact that lasers by comparison have a much smaller efficiency, which for a rocket propulsion system requires a much larger waste heat rejection system.
However, with the concept of staged thermonuclear micro-explosions, detailed below, the initial trigger energy conceivably can be made so small that highly efficient gas lasers, such as the CO2, laser, cannot be ruled out. Therefore, one can think of a basic IFE propulsion concept, as shown on Figure 4.

Inertial fusion propulsion system (Orion Project).
A crucial improvement for the nuclear pulse rocket concept results in combining thermonuclear micro-explosion with strong magnetic reflectors. Magnetic reflectors of the required strength turn out to be feasible with superconducting magnetic field coils. The thermonuclear micro-explosion reaction should preferably produce little or no neutron radiation which would penetrate into the spacecraft, thereby creating in it a large heat source and which would drastically increase the heat rejection system. One good candidate meeting the requirement of low neutron radiation is again the DHe3 thermonuclear reaction.
If one desires to use a thermonuclear fuel, (1) it is abundant and (2) it leads only to charged fusion products, one is then led to the reaction H + B11 → 3He4, where B11 is sufficiently abundant in the required amounts. The HB11 reaction also satisfies the condition that the reaction will only lead to charged fusion products. The next reaction in line is H + Li7 → 2He4, depending on the much less abundant Li7 isotope. Under the light elements, only the reaction H + N15 → He4 + C12 seems promising, but it depends on the relatively rare N15 isotope (Winterberg, 1977).
The ignition of these reactions is much more difficult to achieve than the DT or even the DHe3 reaction. Typically ignition energies larger than ∼ 103 may be required. These larger ignitions necessitate a correspondingly larger energy storage system which presents a serious problem for mobile propulsion systems. However, if the concept of staged thermonuclear micro-explosions is used, whereby a smaller micro-explosion ignites a subsequent larger one, the ignition of such reactions as the HB11 reaction suddenly comes within reach. The staging of thermonuclear micro-explosions may pose an economic problem for an earthbound power plant, where the cost of the thermonuclear target has to be kept low, but in case of a propulsion system, no such economic considerations are entered. In this concept, one may use for the first stage the easily ignitable DT reaction to be followed by a second stage HB11 micro-explosion, ignited by the first stage DT micro-explosion. If the energy output of the second stage is, for example, ∼ 102 times larger, than for the first stage, only a small relative fraction of neutrons are produced.
One may think that the same end could also be reached by mixing DT with HB11. However, because of the much higher burn rate in DT, the energy released by the DT reaction will be uselessly dissipated long before the HB11 gets started. Furthermore, mixing a small amount of DT with a large amount of HB11, as would be required to ignite a large amount of HB11 with a small amount of DT, would dilute the DT to such a degree that the thermonuclear ignition of the DT contained in this mixture would become very difficult. The only way out of this dilemma, therefore, seems to be in the concept of staged thermonuclear micro-explosions.
There are three likely possibilities by which this may be achieved. The first possibility is based on a shock wave lens, the second on a shock wave mirror, and the third one on the adiabatic Prandtl–Meyer flow. All three staging methods require additional material reducing the overall specific impulse. This may not pose a serious drawback in a propulsion system to serve for transportation within our planetary system, but it will in one designed for interstellar missions requiring the highest possible specific impulse in order to bring down the transit times to a few decades, less than a human lifetime. In aiming at the highest possible specific impulse, we thus propose as a fourth staging principle, a method based on staged magnetic reflectors produced by superconducting magnetic field coils. Technically, this is probably the most difficult way to realize staging, but the most rewarding one in terms of efficiency.
5. MATTER-ANTIMATTER ANNIHILATION
5.1. General
Devotees of Star Trek will need no reminding that the starships Enterprise and Voyager are powered by engines that utilize antimatter. Far from being fictional, the idea of propelling a spacecraft by the annihilation of matter, and antimatter is being actively investigated at NASA's Marshall Space Flight Center, Pennsylvania State University, and elsewhere. The principle is simple: an equal mixture of matter and antimatter provides the highest energy density of any known propellant. Whereas the most efficient chemical reactions produce about 1 × 107 J/kg, nuclear fission 8 × 1013 J/kg, and nuclear fusion 3 × 1014 J/kg, the complete annihilation of matter and antimatter, according to Einstein's mass-energy relationship (E = mc2), yields 9 × 1016 J/kg. In other words, kilogram for kilogram, matter–antimatter annihilation releases about 10 billion times more energy than the hydrogen/oxygen mixture that powers the Space Shuttle main engines, and 300 times more than the fusion reactions at the Sun's core. However, there are several technical hurdles to be overcome before an antimatter rocket can be built. The first is that antimatter does not exist in significant amounts in nature, at least, not anywhere near this solar system. It has to be manufactured. Currently the only way to do this is by energetic collisions in giant particle accelerators, such as those at the Fermi Laboratory (USA) and CERN (Switzerland) (Gabrielse et al., 2002; Hangst et al., 2002). The process involves accelerating protons to almost the speed of light and then slamming them into a target made of a metal such as tungsten. The fast-moving protons are slowed or stopped by collisions with the nuclei of the target atoms, and the protons kinetic energy converted into matter in the form of various subatomic particles, some of which are antiprotons—the simplest form of various subatomic particles. So efficient is matter–antimatter annihilation, that 71 milligrams of antimatter would produce as much energy as that stored by all the fuel in the Space Shuttle external tank. Unfortunately, the annual amount of antimatter (in the form of antiprotons) presently produced at Fermi Laboratory and CERN is only 1–10 ng (Smith et al., 1999; Schmidt et al., 1999).
On top of this production shortfall, there is the problem of storage. Antimatter cannot be kept in a normal container because it will annihilate instantly on coming into contact with the container's walls. One solution is the Penning Trap—a super cold, evacuated electromagnetic bottle in which charged particles of antimatter can be suspended. Antielectrons or positrons are difficult to store in this way, so antiprotons are stored instead. Penn State and NASA scientists have already built such a device capable of holding 10 million antiprotons for a week. Now they are developing a Penning Trap with a capacity that is 100 times greater (Smith et al., 1999). Basic features of a Penning Trap are depicted in Figure 5.

Penning trap for antiprotons ions.
At the same time, Fermi Laboratory is installing new equipment that will boost its production of antimatter by a factor of 10–100.
A “spacecraft” propulsion system that works by expelling the products of direct one-to-one annihilation of protons and antiprotons—a so-called beamed core engine (Fig. 6) would need 1–1000 g of antimatter for an interplanetary or interstellar journey (Forward, 1985a, 1985b; Hora & Loeb, 1986).

Schematic of an idealized antiproton rocket. (beamed core engine).
Even with the improved antiproton production and storage capacities expected soon, this amount of antimatter is beyond our reach. However, the antimatter group at Penn State has proposed a highly efficient space propulsion system, which would need only a tiny fraction of the antimatter consumed by a beamed core engine. It would work by a process called antiproton-catalyzed micro-fission/fusion (ACMF) (Smith et al., 1999; Gaidos et al., 1998a, 1998b).
5.2. ACMF and ICAN-II
Antimatter annihilation, nuclear fission, and nuclear fusion all have major problems. Antimatter annihilation requires antimatter, which is hard to come by in this matter filled world. Fission produces a lot of radioactive waste, as well as being the least efficient of the three. Fusion is hard to get started and sustain (the Sun is able to sustain its fusion reaction only because of its immense gravitational field). However, in a wonderful example of, the sum of the parts not being equal to the whole, by combining these three problematic energy sources, all of these problems are minimized. Very little antimatter is needed (just enough to start the fission reaction), very little fission occurs (just enough to start the fusion reaction), and the fusion reaction does not have to be sustained for very long (the drive uses pulses of thrust). It has already been well demonstrated that a fission reaction can be sufficient to ignite a fusion reaction (i.e., the Hydrogen Bomb), and Penn State has recently demonstrated that a relatively small number of antiprotons can be used to ignite a fission reaction.
A pellet of Deuterium, Tritium, and Uranium-238 (nine parts Deuterium-Tritium (D-T) for every one part U238) is injected into the reaction chamber. First the pellet is compressed using ion particle beams, then irradiated with a 2 ns burst of antiprotons. The antiprotons annihilate some of the pellet, producing enough energy to cause the U238 to fission. In turn, the fission reaction ignites a fusion reaction within the D-T core. The fusion reaction produces the desired engine thrust. A new pellet is than inserted, and the process repeats itself (see Fig. 7).

Pellet construction and geometry.
The antiproton triggering of the process is made easier by annihilation within U238 pastille initially stopping antiproton beam.
The drive concept seems to be the most efficient (as determined by NASA) for use in manned, planetary missions. A round-trip, manned mission to Mars using the ACMF drive would only take 120 days, and require approximately 140 ng of antimatter (which could be produced in one year by Fermi laboratory after a few major upgrades are implemented). In addition, it would require approximately 362 metric tons of propellant (the D-T-U pellets).
Penn State University has designed a spacecraft, called ICAN-II, than would use the ACMF drive for omni planetary mission within the solar system. Figure 8 is a rendering of what the ICAN-II spacecraft would look-like if built.

ICAN-II project.
ICAN-II is similar to the ORION spacecraft design put forth by Stanislaw Ulam in the late 1950 (Dyson, 1968). The ORION was intended to be used to send humans to Mars and Venus by 1968. It was to utilize a large number of nuclear bombs that would be set off one after the other, behind the ship to push it forward. It would, of course, require large shock-absorbers and ablative shielding for its pusher-plate. The ICAN-II also, in a sense, utilizes nuclear “bombs” for thrust. However, instead of regular fission bombs like the ORION would utilize, ICAN-II uses what are, essentially, a large number of very small hydrogen-bombs. Set off, of course, by a stream of antiprotons. Ecological concerns would probably require that the ICAN-II be assembled in space. Of course, a precedent for such large scale orbit-based assembly is already being set by the construction of the International Space Station.
The radiation from ICAN-II's ACMF engine would be intercepted by a 4 meter radius silicon carbide shell. Additionally, 1.2 meters of lithium hybrid will shield the fuel rings from high-energy neutrons that are ejected from the nuclear explosions, and 2.2 meters of shielding will protect the crew modules. The spacecraft would have a total mass of 625 metric tons, with 82 additional metric tons available for payload. This is more than sufficient to carry a Mars Lander and exploration vehicles.
The ICAN-II is a viable spacecraft design that could be built within the next two decades. Currently, antiprotons can only be stored for a few weeks and production is very low, but the problems with the storage and production are engineering problems, not physical problems.
Estimates of component masses for a return trip in 120 day, ΔV = 100 km/s Mars mission (RT) are shown in Table 4.
Estimate of ICAN-II Vehicle Masses for 120 days, ΔV = 100 km/s Mars/Mission (RT)

Figure 9 shows the thrust and ISP for a 1 Hz firing rate. For a ΔV of 100 km/s and an Isp of 13500 s (200 g WLS), 362 metric tons of propellant are required for a 345 metric tons ICAN II dry mass (see Table 3). With a 200 g WLS, the thrust is about 100 kN, which accelerates the outbound craft to a 25 km/s ΔV in 3 days. For 800 g of ejected mass, about 30 ng of antiprotons are required. Hence, ICAN-II could be fueled with one year's production of antiprotons at Fermi Laboratory, estimates to be approximately 140 ng by the year 2010.

Thrust and Isp versus propellant at 1 Hz.
Reference Missions

Utilizing the vehicle performance parameters presented above, three potential ICAN-II missions were analyzed (Gaidos et al., 1998a, 1998b). As an intermediate step to a full non–impulsive analysis, simulations of vehicle trajectories within planetary gravitational spheres of influence were performed, by modeling vehicle thrust and solar gravity as perturbations. The results indicate that the majority of the ΔV was gained within the planetary spheres of influence, permitting the design of interplanetary trajectories using impulsive maneuvers at the endpoints. Missions to Mars, Jupiter, and Pluto were investigated, and the results are presented in Table 6. The short transfer times significantly alleviate psychological and physical dangers to the crew. A total ΔV requirement of 120 km/s was stipulated to provide a large launch window every two years, although the mission can be completed with as little as 70 km/s if departure is timed correctly.
Examples of ICAN-II capabilities

Whereas conventional nuclear fission can only transfer heat energy from a uranium core to surrounding chemical propellant, ACMF permits all energy from fission reactions to be used for propulsion. The results are a more efficient engine that could be used for interplanetary manned missions. The ICAN-II spacecraft designed at Penn State would use the ACMF engine and only 140 ng of antimatter for a manned 30-day trip to Mars.
A follow-up to ACMF and ICAN is a spacecraft propelled by antiproton initiated micro-fission/fusion (AIM) in which a small concentration of antimatter and fissionable material would be used to spark a micro-fusion reaction with nearby material. Using 30–130 μg of antimatter, an unmanned AIM-powered probe –AIMStar– would be able travel to the Oort cloud in 50 years, while a greater supply of antiprotons might bring Alpha Centauri within reach (Fig. 10).

Expanded side view of the AIMStar reaction trap (Gaidos et al., 1998a, 1998b).
Combining antimatter technology with the concept of the space sail has also led to the idea of the antimatter–driven sail (Howe & Metzger, 1989; Howe & Jackson, 2004).
5.3. Antimatter propulsion concepts
In view of the important energy losses arising in the p − p annihilation through ultimate neutrino energy production (∼ 50% of total reaction energy), an important aspect of all antimatter–powered propulsion concepts, is to utilize the products as soon as possible after the original pp reaction, when most of the product energy is tied up in a charge state. This entails either, (1) using the products to heat a reaction fluid through fluid/product collisions or an intermediate material, or (2) directing the highly energetic charged pions or muons out a magnetic nozzle to produce thrust. The propulsion concepts that employ these mechanisms generally fall into four categories: (1) solid core, (2) gaseous core, (3) plasma core, and (4) beamed core configurations.
The solid core concept (Howe & Metzger, 1989) uses antiprotons to heat a solid, high-atomic weight (Z), refractory metal core. Propellant is pumped into the hot core and expanded through a nozzle to generate thrust. The performance of this concept is roughly equivalent to that of the nuclear thermal rocket (Isp ∼ 103 s), due to temperature limitations of the solid. However, the antimatter energy conversion and heating efficiencies are typically high due to the short mean path between collisions with core atoms (ηe ∼ 85%).
The gaseous core system (Cassenti, 1991) substitutes the low–melting point solid with a high temperature gas, thus permitting higher operational temperatures and performance (Isp ∼ 2 × 103 s). However, the longer mean free path for thermalization and absorption results in much lower energy conversion efficiencies (ηe ∼ 35%).
One step beyond these concepts is the plasma core, where the gas is allowed to ionize and operate at even higher effective temperatures. Heat loss is suppressed by magnetic confinement in the reaction chamber and nozzle. Although performance is extremely high (Isp ∼ 104–105 s), the long mean free path results in very low energy utilization (ηe ∼ 10%)
The “ultimate” system is the beamed core concept (Forward, 1985a, 1985b; Cassenti, 1991; Frisbee & Leifer, 1998) which avoids the problems of heating a secondary fluid altogether. Here the charged products of the proton–antiproton annihilation are directly expelled from the vehicle along an axial magnetic field. The exhaust velocities of these products are exceptionally high (Isp ∼ 107 s), approaching the speed of light. Although energy utilization efficiencies are also high (ηe ∼ 60%), the flow rate and thrusts are typically very low.
In addition to these pure-antimatter systems, there are several concepts which utilize antiprotons driver to catalyze and initiate a hybrid fission/fusion process (Sec. 5.2) in a compressed plasma or condensed material target. Practically all of the propulsive energy in these cases is derived from fusion reactions. Consequently, antimatter requirements are much lower than those of pure-antimatter systems.
The first of such processes is ACMF, detailed at length in Section 5.2. Here a pellet of D-T and U238 is compressed with particle beam and irradiated with a low-intensity beam of antiprotons. The antiprotons are readily absorbed by the U238 and initiate a hyper–neutronic fission process that rapidly heats and ignites the D-T core. The heated fission and fusion products expand to produce thrust, but the inherent isotropy of the flow results in a lower effective energy utilization and jet efficiency. Although additional thrust is obtained from an ablating surface that absorbs neutrons and electromagnetic radiation from the ignited pellet, the performance of this concept is lower than the plasma and beamed core rockets (Isp ∼ 13,500 s). Gaidos et al. (1998a, 1998b) have shown that the interaction between the antiproton beam and target exhibits extremely high-gain yielding ratio of fusion energy to antimatter rest mass energy, β, of 1.6 × 107. However, energy utilization is also lower due to the isotropic expansion process (ηe ∼ 15%). Assuming a three-order of magnitude improvement in the efficiency of producing antiprotons over current values, the net energy gain is 640.
5.4. AIM Star
Another concept is antimatter-initiated micro-fusion (AIM) (Gaidos et al., 1998a, 1998b). Here non-neutral plasma of antiprotons within a special Penning trap is repetitively compressed via combined electric and magnetic fields. Droplets containing D-T or DHe3 mixed with a small concentration of a metal, such as Pb208 or U238, are synchronously injected into the plasma (see Fig. 10). The main mechanism for heating the liquid droplet is antimatter-induced fission fragments which have a range of 45 μm in the droplet. The power density released by the fission fragments into the D-T or DHe3 is about 5 × 1013 W/cm3, which is enough to completely ionize and heat the fuel atoms to fusion ignition. The heated products are directed out magnetic field lines to produce thrust. The Isp and energy efficiently for this concept are higher than ACMF (Isp ∼ 67,000 s and ηe ∼ 84% with DHe3, and Isp ∼ 61000 s, and ηe ∼ 69% with D-T). The gains β are 10 for DHe3 and 2.2 × 104 for D-T. Again assuming a three-order of magnitude improvement in antiproton production efficiency, these gains are near break even in terms of net energy flow.
Typical parameters for missions to Oort cloud are given in Table 4. A possible AIMStar design is depicted in Figure 11 as an automatic vehicle

Profile of the AIMStar spacecraft.
Figure 12 shows the ratio of antimatter mass to vehicle dry mass for each concept over the ΔV range. For missions within the solar system and into near interstellar space, antimatter requirements for the catalyzed concepts are many orders of magnitude lower than their pure antimatter counterparts. At a point well beyond the solar system when considering missions to interstellar space, beamed core becomes superior.

Antiproton mass requirements for various antimatter propulsion concepts.
ACMF is clearly superior to all other concepts in terms of antimatter efficiency. This continues until we consider trips to Oort cloud and beyond. At this point the better performance with AIM overtakes ACMF and results in lower antimatter usage. ACMF's requirement is generally two orders of magnitude less for missions within the solar system.
6. SUMMARY
We have demonstrated the enormous potentialities afforded by thermonuclear fusion to the future of space propulsion throughout the solar system.
A decisive and first step beyond SCP might well be afforded by a clean combustion of fission, p-annihilation with inertial compression of DT or D-3He fuel.
However, the slow albeit continuous progresses achieved by MFE and ICF could open the door to many more productive scenario.
We did not discuss costs per se, because those would have been framed very differently for space propulsion than for energy production on earth. It should also be recalled that when thermonuclear energy is affordable, the cost of electricity might well be dropping by several orders of magnitude. So, even p-p annihilation could prove economically practical in a distant future.
It is now widely accepted that present technology could permit to envision ambitious robotic and manned exploration of the solar system, precursor interstellar study of phenomena outside the solar system, and missions to our closest stellar neighbors. These reflect the data used in a recent evaluation of propulsion options for interstellar missions [25]. The missions and their associated ΔV's are shown in Table 3.
A final optimistic touch arises from the steadily increasing antiproton production displayed in Figure 13.

Antiproton production history.





















