Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T23:21:44.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Field distribution, HPM multipactor, and plasma discharge on the periodic triangular surface

Published online by Cambridge University Press:  14 April 2010

C. Chang ,
G.Z. Liu ,
J.Y. Fang ,
C.X. Tang ,
H.J. Huang ,
C.H. Chen ,
Q.Y. Zhang ,
T.Z. Liang ,
X.X. Zhu  and
J.W. Li
C. Chang*
Affiliation:
Department of Engineering Physics, Tsinghua University, Beijing, China
G.Z. Liu
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
J.Y. Fang
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
C.X. Tang
Affiliation:
Department of Engineering Physics, Tsinghua University, Beijing, China
H.J. Huang
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
C.H. Chen
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
Q.Y. Zhang
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
T.Z. Liang
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
X.X. Zhu
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
J.W. Li
Affiliation:
Northwest Institute of Nuclear Technology, Xi'an, Shaanxi, China
*
Address correspondence and reprint requests to: Chao Chang, Northwest Institute of Nuclear Technology, P.O. Box 69-13, No. 28, Pingyu Road, Ba Qiao Xian, Shaanxi, People's Republic of China710024. E-mail: changc02@mails.tsinghua.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

The field distribution and the restraint effect of multipactor and plasma discharge on the periodic triangular surface have been theoretically and experimentally analyzed. It has been found by computational and simulative analysis that the periodic profile can quickly restrain or weaken multipactor and plasma discharge in low pressure within several microwave periods. Considering the field enhancement, increasing the slope angle, advancing the electric field, and lowering the frequency can enhance the multipactor suppression. X-band giga-watt high power microwave experiment with 20 ns short pulse was conducted. It was demonstrated that the periodic profile can effectively improve the breakdown threshold and slower the speed of tail erosion.

Keywords

Dielectric breakdownHigh power microwaveMultipactor and plasma suppressionPeriodic triangular surface
Type
Research Article
Information
Laser and Particle Beams , Volume 28 , Issue 1 , March 2010 , pp. 185 - 193
Copyright
Copyright © Cambridge University Press 2010

INTRODUCTION

Flashover, discharge, and breakdown have played important roles on high power systems and applications (Li et al., Reference Li, Liu, Cheng, Chang, Wan and Wen2009; Mao et al., Reference Mao, Zou, Wang, Liu and Jiang2009; Tarasenko et al., Reference Tarasenko, Baksht, Burachenko, Kostyrya, Lomaev and Rybka2008; Burdovitsin & Oks, Reference Burdovitsin and Oks2008; Kolacek et al., Reference Kolacek, Schmidt, Prukner, Frolov and Straus2008) such as high voltage switch (Wang et al., Reference Wang, Hu and Song2005; Zhang et al., Reference Zhang, Tang, Huang, Qiu, Guan and Wang2008), high power microwave (HPM) transmission (Ali, Reference Ali1988), and HPM radiation antenna (Li et al., Reference Li, Yuan, Zhang, Shu and Zhang2008). With the development of giga-watt (GW) HPM sources (Korovin et al. Reference Korovin, Kurkan, Loginov, Pegel, Polevgin, Volkov and Zherlitsyn2003; Liu et al. Reference Liu, Xiao, Chen, Shao, Hu and Wang2008), dielectric breakdown has been a major factor of limiting HPM transmission and radiation (Chang et al., Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008; Neuber et al., Reference Neuber, Dickens, Hemmert, Krompholz, Hatfield and Kristiansen1998, Reference Neuber, Edmiston, Krile, Krompholz, Dickens and Kristiansen2007). Periodic rectangular (Chang et al., Reference Chang, Huang, Liu, Chen, Hou, Fang, Zhu and Zhang2009c) and triangular (Chang et al., Reference Chang, Liu, Huang, Chen and Fang2009d) surface profiles have been found to increase the breakdown threshold of dielectric window at the vacuum side, by the theoretical analysis and recent experiments with megawatts (MW) power, μs pulse width, and S band frequency. However, the theory needs improvement since the field distribution will be significantly influenced by the periodic surface profile. What is more, for HPM with GW power and ns short pulse, rapid plasma avalanche in the fast established local high pressure above the dielectric surface leads to microwave tail erosion (Chang et al., Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008, Reference Chang, Liu, Zhu, Chen and Fang2009a, Reference Chang, Liu, Tang and Yan2009b). There is still no research about the effect of periodic triangular surface on multipactor and plasma discharge under HPM short pulse and local surface pressure. In this article, we try to study the problems mentioned above via analytical analysis, particle in cell (PIC) simulation, and GW X-band HPM experiment.

FIELD DISTRIBUTION AND DYNAMIC ANALYSIS

Field Distribution on the Triangular Surface

In order to simplify the analytical calculation, microwave magnetic field has been neglected, and only the electric field rather than electromagnetic field is considered. This approximation is appropriate when microwave magnetic force is much smaller than electric force for electron energy ɛe < 1 keV and velocity ratio v/c << 1. The periodic surface can effectively decrease ɛe to be lower than the first crossover energy of secondary emission yield (SEY). Besides, microwave magnetic force was also neglected and only electric force was considered in analyzing HPM multipactor on the dielectric (Valfells et al., Reference Valfells, Verbonceour and Lau2000; Chang et al., Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008, Reference Chang, Huang, Liu, Chen, Hou, Fang, Zhu and Zhang2009c).

In order to solve the rf field on the periodic triangular surface, electrostatic field distribution is first deduced, which is appropriate since the periodic distance L is much smaller than a wavelength. Referring to Figure 1, the tangent field is E y0, the slope angle is ξ, the angle between the slopes is 2α, and the slope length is d. In the two-dimensional (2D) polar system, the electric potential Φ(r, θ) satisfies Laplace equation and odd symmetry to the plane θ = 0. The respective potential Φ(r, θ) in the vacuum and in the dielectric can be approximately written as Φ1 = A 1r nsin(nθ), and Φ2 = A 2r nsin(n(π−θ)), where n must be positive since potential is finite at r = 0. Φ and ɛ∂Φ/∂θ are continuous on the vacuum/dielectric boundary of θ = α, which yields the boundary condition equation:

(1)
\varepsilon _{\rm 1}{\rm /}\varepsilon _{\rm 0} \tan \lpar n\alpha \rpar +\tan \lpar n\lpar \pi - \alpha \rpar \rpar =0.

Fig. 1. Schematic of field and potential distribution using polar system on the periodical triangular surface.

The electrostatic field $\overrightarrow E _{es}= - \nabla \Phi$ between the slopes is approximately given by:

(2)
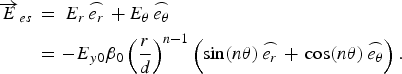
\eqalign{\overrightarrow E _{es} \,& = \, E_r \mathop{e_r}\limits^{\frown} \, + \, E_\theta \mathop{e_{\theta}}\limits^{\frown} \cr &=- E_{y0} \beta _0 \left({\displaystyle{r \over d}} \right)^{n - 1} \left({\sin \lpar n\theta \rpar \mathop{e_r}\limits^{\frown} \, + \,\cos \lpar n\theta \rpar \mathop{e_{\theta}}\limits^{\frown}} \right).}

Where β0 is the correction coefficient. Define field enhancement factor β ≡ E es/E y0. By numerical calculation, the smallest positive root of Eq. (1) is n ∈ (0,1) for ɛ1/ɛ0 > 1, thereby, both E r0 and E θ0 are advancing with the decrease of r and the ratio E r/E θ = tan(nθ) is independent of r. Similar to the analysis of triple junction in Jordan et al. (Reference Jordan, Lau, French, Gilgenbach and Pengvanich2007), by transformation from cylindrical to Cartesian complex coordinate system, and the field in Eq. (2) can be expressed as:

(3)
\overrightarrow E_{\!\!es}=- E_{y0} \beta _0 \left({\displaystyle{r \over d}} \right)^{n - 1} \left({\sin \left({\lpar n - 1\rpar \theta } \right)\hat e_x+i\cos \left({\lpar n - 1\rpar \theta } \right)\hat e_y } \right)

Furthermore, $\overrightarrow E_{\!\!es}$ can be described as $\overrightarrow E_{\!\!es}=$$- iE_{y0} \beta _0 \left({S^{\ast} /d} \right)^{n - 1}$, where S ≡ re iθ = x + iy is the complex variable and S* is the complex conjugate of S. According to Eqs. (2) and (3), the rf field with the frequency ω and emission phase φ reads $\overrightarrow E_{\!\!rf}=\overrightarrow E_{\!\!es} \sin \!\lpar \omega t+\varphi \rpar$.

Dynamic Analysis

Under the rf field $\overrightarrow E _{\!\!rf}$ and at local pressure, the gases molecular on the periodic triangular surface are ionized by seed electrons, and electron and ion pairs are produced. The motions of plasma electrons can be described as follows: (1) reciprocating flying between the slopes and ionizing the gas molecular, (2) impacting as well as multipactoring along the slopes until the rf field reversing.

First, the motion of electron multipactoring along the slope is analyzed. Under the tangent field along the slope E r(θ = α)sin(ωt + φ), the normal field E θ(θ = α)sin(ωt + φ) and positive charge field E DC, the tangent and normal components of the electron velocity after considering ionization and collision can be described as (Chang et al., Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008):

(4)
\displaystyle{{du_t \lpar t\rpar } \over {dt}}+\nu _t u_t \lpar t\rpar +\displaystyle{{eE_r \lpar \alpha \rpar \sin \lpar \omega t+\phi \rpar } \over m}=0\comma \;
(5)
\displaystyle{{du_n \lpar t\rpar } \over {dt}}+\nu _t u_n \lpar t\rpar +\displaystyle{{eE_{DC} } \over m}+\displaystyle{{eE_\theta \lpar \alpha \rpar \sin \lpar \omega t+\phi \rpar } \over m}=0\comma \;

Where νt = νm + νi, ν i is the ionization frequency, and ν m is the collision frequency for momentum transfer. Solving Eqs. (4) and (5), u t and u n are derived as:

(6)
\eqalign{& u_t \lpar t\rpar = \displaystyle{{eE_r \lpar \alpha \rpar \exp \left({ - \nu _t t} \right)} \over {m\lpar \omega ^2+\nu _t^2 \rpar }}\left({\nu _t \sin \phi - \omega \cos \phi } \right)\cr & - \displaystyle{{eE_r \lpar \alpha \rpar } \over {m\lpar \omega ^2+\nu _t^2 \rpar }}\left({\nu _t \sin \lpar \omega t+\phi \rpar - \omega \cos \lpar \omega t+\phi \rpar } \right)}\comma \;
(7)
\eqalign{& u_n \lpar t\rpar =\displaystyle{{eE_\theta \lpar \alpha \rpar \exp \left({ - \nu _t t} \right)} \over {m\lpar \omega ^2+\nu _t^2 \rpar }}\left({\nu _t \sin \phi - \omega \cos \phi } \right)\cr & - \displaystyle{{eE_\theta \lpar \alpha \rpar } \over {m\lpar \omega ^2+\nu _t^2 \rpar }}\left({\nu _t \sin \lpar \omega t+\phi \rpar - \omega \cos \lpar \omega t+\phi \rpar } \right)\cr &- \displaystyle{{eE_{DC} } \over {m\nu _t }}+\exp \lpar - \nu _t t\rpar \left({u_{z0}+\displaystyle{{eE_{DC} } \over {m\nu _t }}} \right).}

The corresponding transit time τ meeting $\vint_0^\tau {u_n \lpar t\rpar } dt=0$ can be calculated by integrating the velocity u n in Eq. (7):

(8)
\eqalignno{& \left({{\rm 1 - }\exp \left({ - \nu _t \tau } \right)} \right)\left({\sin \phi - \displaystyle{\omega \over {\nu _t }}\cos \phi+\displaystyle{{m\lpar \omega ^2+\nu _t^2 \rpar } \over {eE_\theta \lpar \alpha \rpar \nu _t }}\left({u_{z0} +\displaystyle{{eE_{DC} } \over {m\nu _t }}} \right)} \right)\cr & \quad +\sin \lpar \omega \tau+\phi \rpar - \sin \phi - \displaystyle{{\nu _t } \over \omega }\left({\cos \phi - \cos \lpar \omega \tau +\phi \rpar } \right) \cr & \quad +\displaystyle{{E_{DC} \lpar \omega ^2+\nu _t^2 \rpar {\rm t}} \over {E_\theta \lpar \alpha \rpar \nu _t }}{\rm=0.} &}

In the initial and developing stage of multipactor, and for sufficiently large slope angle θ and most phases φ, it meets E θ >> E DC, and E DC can be neglected. Thus, the multipactor is mainly determined by the rf electric field.

Second, for flight between the two slopes, the complex electron velocity equation under rf field in Eq. (3) should meet:

(9)
\eqalign{&\displaystyle{{d\left({u_x+iu_y } \right)} \over {dt}}+\nu _t \left({u_x+iu_y } \right) \cr & +\left({\displaystyle{{S^{\ast} } \over d}} \right)^\nu \displaystyle{{\,ieE_{y0} \beta _{\rm 0} \sin \lpar \omega t+\phi \rpar } \over m}=0.}

This equation is equivalent to:

(10)
\displaystyle{{d^{\rm 2} S} \over {dt^{\rm 2} }}+\nu _t \displaystyle{{dS} \over {dt}}+\left({\displaystyle{{S^{\,\ast} } \over d}} \right)^\nu \displaystyle{{ieE_{y0} \beta _{\rm 0} \sin \lpar \omega t+\phi \rpar } \over m}=0.

Results

By numerically calculating the smallest positive root n in Eq. (1) and substituting n in Eq. (2), comparison of analytical and simulative value β on the periodic triangular surface is shown in Figure 2. In order to fit the simulation result of 2D electromagnetic wave at 9.6 GHz and ɛ = 4, it takes β0 = 1.15 and the corrective ɛ = 9. It's illustrated in Figure 2 that β is advanced with the decrease of r/d.

Fig. 2. Comparison of analytical β with 2D electromagnetic simulation results as a function of r/d and slope angle.

In order to reach the plasma critical density n c in a short pulse τ, the surface pressure should be sufficiently high and can be approximately estimated. Assuming the surface pressure rising linearly with time, the ionization rate can be described as ν i = ν i/p*(at + p 0), where p 0 is the initial pressure, and ν i/p ~ 5 × 109/(s*Torr) approximately keeps constant for electron energy with several hundred eV (Chang et al., Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008). The electron density meets: $n=n_0 \exp\; (\int_{\!0}^{\tau} \nu_i\, dt)$, thus, ln(n c/n 0) – ν i/p*(aτ2/2 + p 0τ) = 0. Set n c/n 0 ~ 108–10, p 0 = 10−4 Torr, and τ = 10–20 ns, the local pressure need to rise to 0.4–0.9 Torr to realize breakdown.

The parameters of collision and ionization frequency with relation to gas pressure and electron energy suited for N2 gas according to Chang et al. (Reference Chang, Liu, Tang, Chen, Qiu, Fang and Hou2008) are adopted. By numerically calculating the transit time τ in Eq. (8) and squaring Eq. (6), the impact energy ɛe within the half period 0.5 T and variation of the ratio of τ and the corresponding 0.5 T are shown in Figures 3a and 3b. The parameters used for calculation are frequency 9.6 GHz and 2.86 GHz, slope angle π/4 and π/3, vacuum and pressure 1 Torr, E y0 70 kV/cm and 30 kV/cm, and u z0 = 1.88 × 106 m/s. In Figures 3a and 3b, β =1 represents no field enhancement, which has been considered for the other curves, and the non-marked pressure and field for the curves are vacuum and 70 kV/cm.

Fig. 3. (a) The impact energy ɛe as a function of phase φ, field E y0, field enhancement factor β, slope angle ξ, and pressure p for f = 9.6 GHz and r/d = 0.3. (b) Variation of the ratio τ/(0.5 T) with φ, E y0, β, ξ, f, and p for r/d = 0.3.

It is shown in Figure 3a that, in most emission phases within the half period, electron energy keeps unchanged and lower than the first cross over energy (about 30–50 eV) of secondary emission yield curve due to weak accelerating force along the slope and strong normal restoring force, leading to multipactor suppressed. Besides, with the slope angle increasing (from π/4 to π/3), the transit time becomes shorter and the energy also decreases, since the tangent accelerating field is reduced and the restoring field is enhanced. Moreover, increasing the field (from 30 kV/cm to 70 kV/cm) will lead to both of the tangent and normal field advancing, therefore, the transit time lowers and the energy changes a little.

That the ratio of τ/(0.5 T) for S band is smaller than that for X band in Figure 3b means that electrons undergo a greater number of impacts with SEY < 1 within the half period, leading to a faster loss of electrons from the discharge. The influence of low pressure on transit time and electron energy is small, because the collision and ionization during the flight distance along the slope is tiny. The plasma electrons impacting the slopes and multipactoring along the slopes will die out, consequently, the periodic slopes can take a role of suppressing multipactor and weakening plasma avalanche.

It can be illustrated in Figure 5 that, both of the tangent and normal field enhancement factor β(r) gradually diminishes with the increase of r/d, E r/E r0 decreases to be lower than one and E θ/E θ0 always keeps higher than one. Therefore, the transit time τ is shorter, impact energy ɛe is lower, and multipactor restraint strengthens compared with no field enhancement (shown in Figs. 3a and 3b).

Since the angle α ∈ (π/6-π/4) is small, the variation of E y and E x with θ has been neglected in approximately calculating Eq. (10). The component E y is dominate and determines the main flight direction of electrons, and the time τ1 for flying between the slopes satisfies Sy = 2*r*sinα. For the periodic structures with the same slope height 1 mm and different slope angles π/4 and π/3, flight time versus half period τ1/(0.5 T) for φ = π/2 is shown in Figure 4. Electrons are emitted perpendicularly to the slope surface with u z0 = 1.88 × 106 m/s. Field enhancement is considered in all curves except for that of β = 1, and the non-marked pressure and frequency for the curves are vacuum and 9.6 GHz.

Fig. 4. Flight time τ1/(0.5 T) as a function of slope angle ξ, vertical height h, field E y0, pressure p and frequency f.

The flight time τ1 becomes shorter after considering field enhancement as shown in Figure 4. With the increase of height h = r*cos α, τ1 is enhanced and the damping effect of gas pressure on reciprocating flight between the slopes aggravates. Thereby, the residual time for electrons multipactoring along the slopes shortens, leading to multipactor restraint weakening, that is to say, multipactor is suppressed faster at the bottom of the slope compared with the top. The damping effect for 1 T under relatively lower slope angle π/4 is evidently stronger than that under π/3, and τ1 under π/4 is obviously longer than that under π/3, thus, increasing the slope angle is beneficial to shorten the flight time τ1 between the slopes, weak the damping effect, and reduce the transit time τ along the slope, as a result, multipactor restraint improves. Advancing the field (from 50 kV/cm to 70 kV/cm) or lowering the frequency (from 9.6 GHz to 2.86 GHz) as shown in Figure 4 will decrease the ratio τ1/(0.5 T), consequently, multipactor can be suppressed better.

It is found in Figure 5 that electrons have the a + x displacement S x during flying along the electric force line from one slope to the other. One reason is that the emitted velocity has the +x component, more importantly, the component E x calculated by Eq. (3) is odd symmetric to the centerline θ = 0, electrons first have accelerated motion toward +x before traversing the centerline, and then are decelerated but still moves toward +x, hence, electrons always have the positive displacement S x. As a result, electrons will gradually move outward during reciprocating flying between the slopes.

Fig. 5. Field enhancement β of E θ/E θ0 and E r/E r0 as a function of r/d, and displacement S x for 70 kV/cm, 9.6 GHz and vacuum.

SIMULATION AND RESULT

In the 2D electromagnetic PIC simulation, the influence of the periodic isosceles triangular surface on multipactor and plasma development under vacuum and low pressure is investigated. Vaughan's (Reference Vaughan1989) secondary emission model is used to calculate the SEY. A plane electromagnetic wave propagated in a double-parallel-plate transmission line at normal incident to the dielectric. The angular distribution for the secondary emitted electrons is a cosine distribution (Bruining, Reference Bruining1954).

The parameters used for simulation are: peak SEY for normal incidence δmax0 = 2.15, the electron energy at the peak ɛmax = 400 eV, the surface roughness k s = 1, the frequency f = 9.6 GHz, the peak electric field E y0 = 50–70 kV/cm, and the background gas N2 with different pressure. It can be shown in Figure 6 that the size of the vector represents the amplitude of the field, thereby, the field obviously strengthens between the periodic slopes and weakens inside the triangular dielectric.

During flying between the slopes, seed electrons ionize the gas and produce plasma electrons, which can secondarily ionize the gas and form self-persistent ionization. The plasma ions are kept static under the high frequency electric field. For field 70 kV/cm and pressure 1 mTorr (three times the experiment pressure), slope angle ξ π/3 and period length L 0.8 mm, the densities of the electrons and ions and the statistic SEY for plasma electrons are respectively shown in Figures 7a and 7b. Multipactor and plasma discharge can be quickly quenched within several microwave periods (such as 1 ns). The decay speed of plasma electrons is slower than that of seed electrons because ionization can compensate for parts of the loss. Thus, for HPM with short pulse width such as 20 ns, the periodic profile can effectively suppress multipactor.

Fig. 6. (Color online) Electric field vector distribution on the periodical triangular surface.

Fig. 7. (a) The densities of seed electrons n se, plasma electrons n e and ions n i at 1 mTorr and 320 mTorr. (b) Statistic SEY for plasma electrons.

The space electric current densities J y perpendicular to the centerline θ = 0 and J x along the center line are investigated. It can be found in Figure 8 that both of J y and J x oscillate in time at twice the microwave frequency, J y has periodic positive and negative value due to electrons two-time reciprocating flying along the field in a microwave period, and J x shows that electrons have a statistical unidirectional motion along the central line. Since the angular distribution for secondary electrons is a cosine distribution, the probability for electrons emitted perpendicular to the slope surface is the largest. And what is more, the field distribution on the profile explained in the dynamic anaylsis leads to electrons gradually flying away from the bottom. That the amplitudes of J y and J x increase at first and then diminish to zero agrees with the variation of plasma electron density n e with time. The transient trajectories of flying upward in Figure 9a also show that electrons have the displacement away from the bottom.

Fig. 8. The space electric current densities J y and J x.

Fig. 9. (a) The transient electron trajectory for 70 kV/cm and 1 mTorr. (b) The transient space electron cloud for 70 kV/cm and 2 mTorr.

With pressure increasing and ionization rate advancing, the density of the space electrons rises and the space distribution broadens as shown in Figure 9b. At pressure 320 mTorr, plasma avalanche develops sharply, and the electrons produced by ionization are far more than that lost on the slopes. In order to explain the periodic profile still has some restraint effect on plasma discharge, only first ionization is considered in the simulation, in other words, the plasma electrons produced by ionization have no secondary effect on ionizing gas but can multipactor on the slopes. The densities of n e and n i at 320 mTorr in Figure 7a illustrate that plasma electrons can quickly die out due to multipactor suppression on the slopes. Consequently, the speed of plasma avalanche under higher pressure on the periodical triangular surface is slower than that on the flat surface.

With the field reduced from 70 kV/cm to 50 kV/cm, the decay speed of SEY and electron density is found to become slower since the flight time τ1 between the slopes gets longer, the transit time τ for electrons multipactoring along the slopes gets longer, and the number of impacts along the slopes decreases. It is discovered in the simulation that, under the same field and pressure, multipactor suppression for ξ π/3 and L 0.8 mm is faster compared with that for ξ π/4 and L 2 mm, being in accordance with theoretical analysis.

EXPERIMENT AND RESULTS

HPM window breakdown experiment, with power 0.5–1.8 GW, at frequency 9.6 GHz, and with 20 ns pulse width, was conducted, and the experimental setup is illustrated in Figure 10. Microwave was radiated to air through the TE11 dominant-mode conical horn with aperture diameter D = 237 mm and outer flange diameter 320 mm. Teflon window with thickness 32 mm satisfying integral multiple of half wavelength had the minimum reflection, and the inner pressure 0.25–0.3 mTorr was acquired by molecular pump. SF6 with pressure higher than 1 atm. was sealed in a balloon with diameter 750 mm and fixed outside of the window.

Directional couplers and detectors were adopted to measure the online incident and reflected power. Far-field radiation power was measured at a distance 7.5 m from the aperture of the horn, satisfying the far-field critical condition 2D 2/λ = 3.6 m. Dielectrics of flat surface, periodical triangular surface with ξπ/3 and L 0.8 mm, as well as that with ξ π/4 and L 2 mm were studied. Field distribution along the vertical radius paralleled with polarization direction of TE11 for 1 GW and the field vector distribution on the aperture are shown in Figures 11a and 11b.

Fig. 10. Basic experiment setup.

Fig. 11. (a) E-field along the vertical radius for 1 GW incident power. E t the tangent field parallel to the surface and E n the normal field. (b) Electric field vector distribution on the aperture.

The relations of radiation power density P rad, pulse width difference ΔT, and reflected power P ref with the incident power P on are shown in Figures 12 and 13. With incident power advancing, for the flat surface, the radiation pulse width gradually gets shorter than the incident width, and the reflected power increases crazily when P on is above 1 GW. The response time for the detectors is about 2 ns, and the slopes of the rising edge and falling edge of different detectors may differ from each other due to the various response characters, consequently, the radiation pulse width may be longer than the incident width. For the sawtooth surface, P ref increases about triple when P on is enhanced from 0.6 to 1.8 GW, and the amplitude of P ref is much smaller compared with that for the flat surface.

Fig. 12. Variation of radiation power density P rad and pulse width difference ΔT with online power P on for (a) flat surface and (b) periodical triangular suface with ξ π/3. Star- P rad; circle-ΔT represents the radiation width subtracting the incident width.

Fig. 13. The ratio of reflected power P ref with the initial P ref0, triangular-flat surface; circle- periodical triangular surface with ξ π/3.

When breakdown happens for the flat surface, obvious tail erosion accompanies with intense reflection peak (shown as α in Fig. 14a) and distinct pressure rising. For the periodical triangular surface, no serious pulse shortening occurs, and the speed of tail erosion is prominently slower than that for the flat surface, whose explanation has been given in the simulation analysis.

Fig. 14. (Color online) Typical breakdown waveforms for (a) flat surface (1.1 GW) (b) periodical triangular surface (1.65 GW) with ξ π/3, top-diode voltage, left-online incident power, medium-radiation power, right-reflected power.

The reflected wave from the dielectric propagates toward the source and couples in the directional coupler, which is used for measuring incident power and has a limited isolation degree and a distance about 1 m from the dielectric surface. Therefore, a small peak shown as β in Figure 14a, whose amplitude is proportional to that of the reflection peak, is followed with the incident pulse after about 10 ns. Similarly, a pulse with flat amplitude and relatively long width (about 20 ns) is found before the reflected peak shown as γ in Figure 14b, caused by a limited isolation degree of the directional coupler used for measuring reflected power.

Before tail erosion, the sawtooth surface with ξ π/3 and L 0.8 mm can transmit the power higher than 1.6 GW and improve the power capacity of about 1.6 compared with that of the flat surface; the corresponding breakdown field exceeds 80 kV/cm. The power capacity for ξ π/4 and L 2 mm attains 1.3 GW, whose reflection amplitude is obviously larger than that for ξ π/3.

DISCUSSION AND CONCLUSION

The periodical slopes can take a role of suppressing multipactor and weakening plasma avalanche, because the plasma electrons impacting the slopes and multipactoring along the slope will quickly die out. Increasing the slope angle is beneficial to reduce the transit time τ and impact energy along the slope, shorten the flight time τ1 between the slopes, and weak the damping effect of gas pressure; advancing the field will shorten τ and τ1; lowering the frequency will decrease the ratio of τ/(0.5 T) and τ1/(0.5 T). Consequently, increasing the slope angle, advancing the field, and lowering the frequency can enhance multipactor restraint.

After considering field enhancement, the transit time τ shortens, impact energy ɛe lowers, and flight time τ1 decreases, thus, multipactor restraint strengthens. The field enhancement factor β improves with the decrease of r/d, thus, multipactor is suppressed faster at the bottom of the slope compared with the top. Electrons gradually move outward during reciprocating flying between the slopes due to the arc field distribution. However, β at the bottom of the sawtooth achieves maximum and is about 5–8 times for slope angle π/4–π/3, that is to say, 400–600 kV/cm may attain at the bottom for E y0 80 kV/cm, as a result, plasma avalanche occurring in the high pressure of the vaporized material induced by bulk breakdown at the bottom leads to microwave tail erosion. The threshold for π/3 is higher than that for π/4 since the restraint effect of plasma discharge for π/3 is stronger.

Multipactor and plasma discharge on the periodic profile can be quickly quenched within several microwave periods, thus, multipactor can be effectively suppressed for HPM with pulse width 20 ns. As a matter of fact, multipactor restraint effect for low frequency and long pulse will be much better than that for high frequency and short pulse, one reason is that lowering the frequency can enhance multipactor restraint, more importantly, the breakdown threshold on the flat surface for the former condition is much lower than that for the latter, and the threshold can be improved limitedly for the latter. For instance, the breakdown threshold for S band and μs width is about 10–20 kV/cm, and that for X band and 20 ns width is higher than 50 kV/cm.

References

REFERENCES

Ali, A.W. (1988). Nanosecond air breakdown parameters for electron and microwave beam propagation. Laser Part. Beams 6, 105–117.CrossRefGoogle Scholar
Bruining, H. (1954). Physics and Application of Secondary Electron. New York: Pergamon.Google Scholar
Burdovitsin, V.A. & Oks, E.M. (2008). Fore-vacuum plasma-cathode electron sources. Laser Part. Beams 26, 619–635.CrossRefGoogle Scholar
Chang, C., Huang, H.J., Liu, G.Z., Chen, C. H., Hou, Q., Fang, J.Y., Zhu, X.X. & Zhang, Y.P. (2009 c). The effect of grooved surface on dielectric multipactor. J. Appl. Phys. 105, 123305.CrossRefGoogle Scholar
Chang, C., Liu, G.Z., Huang, H.J., Chen, C.H. & Fang, J.Y. (2009 d). Suppressing high-power microwave dielectric multipactor by the sawtooth surface. Phys. Plasmas 16, 083501.CrossRefGoogle Scholar
Chang, C., Liu, G.Z., Tang, C.X. & Yan, L.X. (2009 b). The influence of space charge shielding on dielectric multipactor. Phys. Plasmas 16, 053506.CrossRefGoogle Scholar
Chang, C., Liu, G.Z., Tang, C.X., Chen, C. H., Qiu, S., Fang, J.Y. & Hou, Q. (2008). The influence of desorption gas to high power microwave window multipactor. Phys. Plasmas 15, 093508.CrossRefGoogle Scholar
Chang, C., Liu, G.Z., Zhu, X.X., Chen, H.B. & Fang, J.Y. (2009 a). Improved model for window breakdown at low pressure. Phys. Plasmas 16, 033505.CrossRefGoogle Scholar
Jordan, N.M., Lau, Y.Y., French, D.M., Gilgenbach, R.M. & Pengvanich, P. (2007). Electric field and electron orbits near a triple point. J. Appl. Phys. 102, 033301.CrossRefGoogle Scholar
Kolacek, K., Schmidt, J., Prukner, V., Frolov, O. & Straus, J. (2008). Ways to discharge-based soft X-ray lasers with the wavelength lambda < 15 nm. Laser Part. Beams 26, 167–178.CrossRefGoogle Scholar
Korovin, S.D., Kurkan, I.K., Loginov, S.V., Pegel, I.V., Polevgin, S.D., Volkov, S.N. & Zherlitsyn, A.A. (2003). Decimeter-band frequency-tunable sources of high-power microwave pulses. Laser Part. Beams 21, 175–185.CrossRefGoogle Scholar
Li, G.L., Yuan, C.W., Zhang, J.Y., Shu, T. & Zhang, J. (2008). A diplexer for gigawatt class high power microwaves. Laser Part. Beams 26, 371–377.CrossRefGoogle Scholar
Li, L.M., Liu, L., Cheng, G.X., Chang, L., Wan, H. & Wen, J.C. (2009). Electrical explosion process and amorphous structure of carbon fibers under high-density current pulse igniting intense electron-beam accelerator. Laser Part. Beams 27, 511–520.CrossRefGoogle Scholar
Liu, G.Z., Xiao, R.Z., Chen, C.H., Shao, H., Hu, Y.M. & Wang, H.J. (2008). Cerenkov generator with coaxial slow wave structure. J. Appl. Phys. 103, 093303.CrossRefGoogle Scholar
Mao, Z., Zou, X., Wang, X., Liu, X. & Jiang, W. (2009). Circuit simulation of the behavior of exploding wires for nano-powder production. Laser Part. Beams 27, 49–55.CrossRefGoogle Scholar
Neuber, A., Dickens, J., Hemmert, D. H., Krompholz, H., Hatfield, L. & Kristiansen, M. (1998). Window breakdown caused by high-power microwaves. IEEE Trans. Plasma Sci. 26, 296–303.CrossRefGoogle Scholar
Neuber, A., Edmiston, G., Krile, J., Krompholz, H., Dickens, J. & Kristiansen, M. (2007). Interface breakdown during high-power microwave transmission. IEEE Trans. Magn. 43, 496–500.CrossRefGoogle Scholar
Tarasenko, V.F., Baksht, E.H., Burachenko, A.G., Kostyrya, I.D., Lomaev, M.F. & Rybka, D.V. (2008). Supershort avalanche electron beam generation in gases. Laser Part. Beams 26, 605–617.CrossRefGoogle Scholar
Valfells, A., Verbonceour, J. & Lau, Y.Y. (2000). Space charge potential distributions in multipactoring electron clouds. IEEE Trans. Plasma Sci. 28, 529.Google Scholar
Vaughan, J. (1989). A new formula for secondary emission yield. IEEE Trans. Electron Devices 36, 1963–1967.CrossRefGoogle Scholar
Wang, X.X., Hu, Y. & Song, X.S. (2005). Gas discharge in a gas peaking switch. Laser Part. Beams 23, 553–558.CrossRefGoogle Scholar
Zhang, Y.M., Tang, J.P., Huang, J.J., Qiu, A.C., Guan, Z.C. & Wang, X.X. (2008). The application of flash-over switch in high energy fluence diode. Laser Part. Beams 26, 213–216.CrossRefGoogle Scholar
Figure 0

Fig. 1. Schematic of field and potential distribution using polar system on the periodical triangular surface.

Figure 1

Fig. 2. Comparison of analytical β with 2D electromagnetic simulation results as a function of r/d and slope angle.

Figure 2

Fig. 3. (a) The impact energy ɛe as a function of phase φ, field Ey0, field enhancement factor β, slope angle ξ, and pressure p for f = 9.6 GHz and r/d = 0.3. (b) Variation of the ratio τ/(0.5 T) with φ, Ey0, β, ξ, f, and p for r/d = 0.3.

Figure 3

Fig. 4. Flight time τ1/(0.5 T) as a function of slope angle ξ, vertical height h, field Ey0, pressure p and frequency f.

Figure 4

Fig. 5. Field enhancement β of Eθ/Eθ0 and Er/Er0 as a function of r/d, and displacement Sx for 70 kV/cm, 9.6 GHz and vacuum.

Figure 5

Fig. 6. (Color online) Electric field vector distribution on the periodical triangular surface.

Figure 6

Fig. 7. (a) The densities of seed electrons nse, plasma electrons ne and ions ni at 1 mTorr and 320 mTorr. (b) Statistic SEY for plasma electrons.

Figure 7

Fig. 8. The space electric current densities Jy and Jx.

Figure 8

Fig. 9. (a) The transient electron trajectory for 70 kV/cm and 1 mTorr. (b) The transient space electron cloud for 70 kV/cm and 2 mTorr.

Figure 9

Fig. 10. Basic experiment setup.

Figure 10

Fig. 11. (a) E-field along the vertical radius for 1 GW incident power. Et the tangent field parallel to the surface and En the normal field. (b) Electric field vector distribution on the aperture.

Figure 11

Fig. 12. Variation of radiation power density Prad and pulse width difference ΔT with online power Pon for (a) flat surface and (b) periodical triangular suface with ξ π/3. Star- Prad; circle-ΔT represents the radiation width subtracting the incident width.

Figure 12

Fig. 13. The ratio of reflected power Pref with the initial Pref0, triangular-flat surface; circle- periodical triangular surface with ξ π/3.

Figure 13

Fig. 14. (Color online) Typical breakdown waveforms for (a) flat surface (1.1 GW) (b) periodical triangular surface (1.65 GW) with ξ π/3, top-diode voltage, left-online incident power, medium-radiation power, right-reflected power.