Feasibility of new laser fusion by intense laser field

K. Imasaki; D. Li

doi:10.1017/S0263034609000354

Feasibility of new laser fusion by intense laser field

Published online by Cambridge University Press: 23 March 2009

K. Imasaki and

D. Li

Show author details

K. Imasaki*: Affiliation:
Institute for Laser Technology, Osaka, Japan
D. Li: Affiliation:
Institute for Laser Technology, Osaka, Japan
*: Address correspondence and reprint requests to: Kazuo Imasaki, Institute for Laser Technology, 2-6 Yamada-oka, Suita, Osaka, 565-0871, Japan. E-mail: kzoimsk@ile.osaka-u.ac.jp.

Article contents

Abstract
INTRODUCTION
MODELING AND ASSUMPTIONS
NUCLEI IN LASER FIELD
NUCLEAR REACTION
ENERGY GAIN BY THE REACTIONS
CONCLUSION
ACKNOWLEDGEMENT
References

Rights & Permissions

Abstract

A feasibility of a new approach of laser fusion in plasma without implosion has been proposed and discussed using an intense laser. The cross-section of nuclear reaction is increased by the enhanced penetrability of nuclei through the Coulomb barrier. In this approach, an intense laser field of more than 10 EW was required to distort the Coulomb barrier to obtain enough penetrability. In the new improved model, a nuclear potential with meson attractive force is considered. Enhancement is observed for penetrability around EW or less power laser due to a nuclear potential. Energy gain even with Deuterium-Deuterium reaction can be obtained on this scheme in Deuterium plasma with energetic nucleon theoretically.

Keywords

Laser fusion Nuclear potential Nuclear reaction Nucleon

Type: Research Article
Information: Laser and Particle Beams , Volume 27 , Issue 2 , June 2009 , pp. 273 - 279

DOI: https://doi.org/10.1017/S0263034609000354 [Opens in a new window]
Copyright: Copyright © Cambridge University Press 2009

1. INTRODUCTION

Intense laser technology is rapidly growing. Various applications have been proposed and tried besides laser fusion. (Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007; Bourdier et al., Reference Bourdier, Patin and Lefebvre2007; Deutsch & Tahir, Reference Deutsch and Tahir2006; Kuehl et al., Reference Kuehl, Ursescu, Bagnoud, Javorkova, Rosmej, Cassou, Kazamias, Klisnick, Ros, Nickles, Zielbauer, Dunn, Neumayer and Pert2007; Kumar et al., Reference Kumar, Gupta and Sharma2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Lie & Imasaki, Reference Li and Imasaki2005; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Sakai et al., Reference Sakai, Miyazaki, Kawata, Hasumi and Kikuchi2006; Sherlock et al., Reference Sherlock, Bell and Rozmus2006; Ostermeyer et al., 2007; Hoffmann et al., Reference Hoffmann, Blazevic, Nt, Rosmei, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005). We have proposed a feasibility of a new approach to laser induced nuclear reaction using intense laser field. An intense laser field distorts the Coulomb barrier, which enhances the tunneling. This forms the cloud by tunneled nucleon and they react when they meet each other. This is a non-Gamov nuclear reaction (Balantekin & Takigawa, Reference Balantekin and Takigawa1998). A more than 10 EW laser was required to distort the Coulomb barrier to obtain enough penetrability for tunneling (Imasaki & Li, Reference Imasaki and Li2008). In this article, improvements for the model and application for Deuterium-Deuterium (D-D) reaction are discussed.

In this article, modeling and assumptions are noted in Section 2 and potentials of the interaction of the nucleus with the laser field are estimated in Section 3. Penetrability of nucleon through Coulomb barrier and formation factor of nuclei with tunneled nucleon as a cloud are noted in Section 4. Energy gain by the D-D reaction in plasma in this scheme is discussed in Section 5 and Section 6 is a summary of the article.

2. MODELING AND ASSUMPTIONS

Around the center of the nuclei, in a previous article, we had assumed a well of nuclear potential with a radius of 5 fm, which is shown in region a by a gray line in Figure 1. But in the actual case, there are mesons at the center of the nucleon, which works as an attractive force. Due to the mesons, the nuclear potential can be shifted as it is presented by the black solid line in Figure 1. This effect is included here in the simple calculation of penetrability.

Fig. 1. Typical potential of nucleus with intense laser.

The Coulomb barrier is dominant in the outer region, and this is schematically shown in region b of Figure 1. In a normal case without intense laser, the field is decayed away with D ⁻¹. Here, D is the distance from the nuclear core center.

At the foot of the Coulomb barrier to the intense laser, the laser field becomes dominant. This is shown in region c of Figure 1, which is a picture at peak laser field. In the laser-dominated region, the field is oscillating with the laser field.

The intense laser is focused and is injected into the plasma as a Gaussian beam. This laser can propagate through the plasma. During this, the intense field of the laser is applied along the center of the laser path. This field distorts the Coulomb barrier in each peak of laser cycle, which promotes the tunneling. The tunneled nucleon forms a cloud of probability of the dimension of the de Broglie wave of the nucleon. The cloud expands with group velocity v _g of the tunneled nucleon. This expansion is kept in the oscillating laser field. When the clouds of tunneled nuclei meet each other, they immediately form a compound nucleus and react as a usual nuclear reaction. This is taking place during the laser pulse.

After the laser pulse, the nuclei with the cloud are diffusing away, so the probability to meet each other rapidly decreases and the reactions are eventually reduced.

The basic assumptions of this model are the following: (1) The plasma has a density up to 10²¹/cm³, which is below the cut-off density of 1 µm meter wavelength of the solid state laser. For simplicity, we assumed the plasma density to be uniform and charge neutral. There are several ways to make long and narrow plasma with sufficient relative velocity. For example, after the injection of a jet of fuel from opposite sides in the reactor, they are irradiated by an appropriate laser pulse from each end before the main pulse. The plasma with a sufficient relative velocity is produced. The plasma shape may have several tens of cm in length with several mm in radius. Such plasma is produced and accelerated by other lasers or ion beams during actual applications (Shimada et al., Reference Shimada, Nisimura, Nakai and Yamanaka2005). (2) The wavelength of the laser is 1.06 µm. The laser technology today for solid-state lasers of 1 µm wavelength is well developed for laser fusion. So the solid-state laser is the first candidate for this intense laser. Its efficiency and repetition rate are being improved for laser fusion driver rapidly. (3) At first, nucleons are trapped in a nuclear potential and hit the inner wall of the Coulomb barrier many times at laser power peak with a nucleon kinetic energy up to 10 eV. The typical mean time of this motion is estimated to be 10⁻²⁰ to 10⁻²¹ s, which is much shorter than the laser peak period. (4) One of the main issues for penetrability is the nucleon energy level. The nucleon distribution in the core is determined by the Fermi-Dirac model as shown in Figure 1. The nucleon in the Coulomb barrier is free from the nuclear potential, so the energy level of the nucleon cannot be determined around the foot of the barrier simply. In this article, the energy level E is considered for a typical level, it is varied from +1 to −5 keV. (5) The typical relation of laser waveform and its defined field peak are shown in Figure 2. The laser peak per one cycle distorts the nuclear Coulomb barrier and promotes the tunneling, and then such a tunneled nucleon forms a cloud around the nuclei. So, the cycle number corresponds to the formation factor of the cloud. (6) A Gaussian laser beam of 2 m in diameter with annular shape for a long and tight focusing is applied. One-sixth of laser pulse is rise time. The power crest lasts about two-third of the time of the laser pulse, and this is an effective period of laser tunneling. After this, the laser pulse is decayed away during one-sixth of the pulse duration. We have set 1/30 of the laser cycle for the laser peak duration. This is shown in Figure 2. It is enough time for a 10 eV proton to tunnel out of the region b of Figure 1 with a nucleon group velocity of 4 × 10⁴ m/s. (7) Clouded nuclei are piled up through the laser pulse. Cloud life is limited by a pion life span of 10 ns in free space, but it is limited by the effective laser pulse due to the diffusion in focusing area for the nuclear reactions. Then the nuclear reaction is decreased rapidly after the laser pulse, which may be shorter than the pion life span. So we set effective reaction duration laser pulse.

Fig. 2. (Color online) Laser cycle and peak power waveform.

3. NUCLEI IN LASER FIELD

3.1. Coulomb Barrier and Nuclear Potential

At the center of the nuclei, there are mesons to combine the nucleon. They reduce the Coulomb potential and cause an attractive force around the center of the nucleon. This force is estimated by the nuclear potential as shown in Figure 3. A simple Coulomb potential shown as a dashed line was used in a previous model. The precise total nuclear potential is estimated by the Yukawa model with appropriate mesons. The difference was recognized around the center at 5 to 10 fm when the model was set and a solid line shown in Figure 3 was obtained. The initial value of the barrier around the core is reduced significantly, which is effective for tunneling and enhances the penetrability.

Fig. 3. (Color online) Natural nuclear potential without laser.

3.2. Coulomb Barrier with Laser Field

The nucleon wave traveling through the Coulomb barrier decays exponentially, and finally it is reflected in most of the cases. When an intense laser is applied, the field in the foot of the Coulomb barrier is distorted at the laser intensity peak. Then the possibility to penetrate the barrier becomes increased.

The field A of the applied laser can be written as

(1)

$A \lpar V/m\rpar = 2.7 \times 10^{3} I^{1/2} \lpar {\rm W}/{\rm cm}^{2}\rpar .$

Here, I indicate the power density of the laser. Within a simple model, the potential induced by the laser field can be written as ϕ_L = −Er, where the field can be given as E = Asin(ωt). Then, we have the total nuclear potential with mesons, Coulomb barrier and laser as

(2)

$\eqalignno{{\rm \varphi}_{total} &= {Z_1 e \over 4{\rm \pi} {\rm \varepsilon}_0 r} + {\rm \varphi}_L - V_0 {e^{-r/r_0} \over r/r_0} \cr &= {Z_1 e \over 4{\rm \pi}{\rm \varepsilon}_0 r} - A \sin \lpar {\rm \omega} t\rpar r - V_0 {e^{-r/r_0} \over r/r_0}.}$

The first term describes the Coulomb field, the second term presents the laser field, and the third term is the nuclear potential with pions. Here we use the Yukawa potential for the pion, where V ₀ = 109 MeV, r is a distance in fm, and r ₀ = 1.13 fm in the usual case.

Let us consider two extreme cases for this potential at the laser peak. We can derive the following equations from Eq. (2). One is

(3)

$U_1 = \left({Z_1 e \over 4{\rm \pi \varepsilon}_0 r} - Ar\right)Z_2 e - V_0 {e^{-r/r_0} \over r/r_0}.$

And the other is

(4)

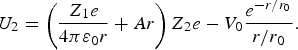
$U_2 = \left({Z_1 e \over 4{\rm \pi \varepsilon}_0 r} + Ar\right)Z_2 e - V_0 {e^{-r/r_0} \over r/r_0}.$

In Eq. (3), one can decrease the barrier. Let us focus on U ₁ providing Z1 = Z2 = 1, then we calculate and figure out U ₁ as shown in Figure 4. Under this assumption, each line of Figure 4 indicates the result for the field at different laser intensity peak obtained solving Eq. (3).

Fig. 4. (Color online) Nuclear potential and Coulomb barrier at various intensity of laser peak.

3.3. Penetrability and Formation Factor

Further, the transmission rate T is calculated using the potential of nuclei discussed in Section 3.2. The transmission rate of the nucleon passing through the barrier may be expressed by

(5)

$T = \exp \Bigg ( \!-\!2{\rm \vint}_R^{R_1} {\rm \beta} \lpar x\rpar dx \Bigg ) \comma$

where

(6)

${\rm \beta} \lpar x\rpar = \left({2m \over \hbar^2}\right)^{1/2} \lsqb U_1 \lpar r\rpar - E\rsqb ^{1/2}$

Here, m = 938.28 MeV/c² is the proton mass, and ħ = 6.58217 × 10⁻¹⁶ × 10⁻⁶ MeVs. Further the penetrability P is defined by

(7)

In a laser peak, f is the mean time of the nucleon collision with the inner wall because of the nuclear potential and the Coulomb barrier. Substituting for the nuclear potential radius, the typical value 5 fm, one finds for f a value of 2000 to 20000 for a nucleon kinetic energy corresponding to 10 eV or 1000 eV during the laser peak. In the actual case, E in Eq. (6) is the kinetic energy of the nucleon. It should be determined by experiments, but for the first simple calculation in this paper, we used values between 0 eV and −10000 eV. Then, the penetrability is calculated as shown in Figure 5 from the Eqs (5), (6), and (7). Figure 5 shows the results of these calculations for various cases.

Fig. 5. (Color online) Penetrability at laser peak power.

Comparing with the quantum well model, significant enhancement was observed in the region of laser power around 10²⁴ to 10²⁶ W/cm². This is due to the nuclear potential effect around the center. A typical group velocity of the nucleon is estimated to be 10⁴ to 10⁵ m/s. From the velocity, a traverse time for 1000 fm is estimated to be 0.01 to 0.1 fs. So, the penetrability obtained in Eq. (5) is valid in our case during the laser peak.

Now we define F as the formation factor of the cloud of the tunneled nucleon after penetration. The probability of the formation of the cloud can be written as

(8)

$F = P \times N_{\rm c}.$

Here N _c is a cycle number of the laser pulse crest. In the present case, 2000 to 20000 can be taken. When F is approaching unity, the saturation with a depletion of the nuclei, and so on, will have taken place. In the calculation presented in Figure 6, this effect is included. In this region, the Fs for the saturation level can be roughly written using F,

$Fs = F/\lpar F + 1\rpar .$

Typical results of Eq. (8) are shown in Figure 6. Here, two cases of cycle numbers are considered, 2000 at 10 ps pulse length and 20000 at 100 ps.

Fig. 6. (Color online) Formation factor of cloud for N _c = 2000 and 20000 in case of f = 1000.

4. NUCLEAR REACTION

In an appropriate time before the main laser pulse, column shaped plasma bulks are produced at each ends of the cylindrical reaction chamber by the laser or the ion beam and are accelerated. They collide with each other at the center with velocity v _r. At this time, the main laser pulse is irradiated, which form the cloud. Here the formation factor is fixed as f = 0.3. The laser intensity and pulse length are fixed as 10^24.5 W/cm² and 10 ps. This model is shown in Figure 7. The radius of the cloud is calculated as

(9)

$r_{\rm eff} = v_{g} \lt\! t\!\gt.$

Fig. 7. Model for nuclear reaction.

Here, v _g is the group velocity of the de Broglie wave of the tunneled nucleon. <t> is an average time of cloud holding in the reacting area. In the period of t, each nucleus has a relative velocity of v _r with cloud density of n _c. We introduce r _eff as a radius of the nucleon cloud, which is diffusing during the laser pulse of 10 ps to 100 ps.

Thereafter, the reaction rate R_r in this model of Figure 7 is written as

(10)

${\bi R}_{\rm r} = F_{1} F_{2} {\rm \pi} r_{\rm eff}^{2} v_{\rm r}.$

In this equation, F1 and F2 are formation factors of laser tunneling nuclei for n ₁ and n ₂ of two species. n ₁ and n ₂ are the number densities of the species in the reacting plasma. In the unit period of t, each nucleus has a relative velocity V _r and a cloud density n _c. This is given by the group velocity of the tunneled nucleon wave and is estimated to be 10⁷ cm/s. So r is 10⁻⁷cm in our case. v is a relative velocity of the nuclei caused by the thermal motion or by the differential acceleration of the particles by the laser. We use a typical velocity of 2 × 10⁸ cm/s.

Then, the reaction rate can be calculated for a density of the plasma using parameters of the relative velocity shown in Figure 8. There is a density limit for laser beam propagation. So the density of the plasma should be less than this parameter, which is shown in Figure 8.

Fig. 8. Relative velocity for reaction rate.

In the actual case, we can choose the particle relative velocity much higher than the usual thermal velocity, when we use a prepulse or double pulse of the laser. When we use a laser to irradiate from opposite sides, we can obtain a relative velocity of more than 10⁸ cm/s, just before the main pulse in this case. These are typical values for the scheme and is summarizes in Table 1.

Table 1. Parameters for gain in Deuteron plasma

5. ENERGY GAIN BY THE REACTIONS

Now the presented simple model is applied for the D-D plasma. The energy from the nuclear reaction is described by E_f and can be written in the form

(11)

$E_{\rm f} = BQ R_{\rm r} n_{1} n_{2} V_{0} t_{\rm L}.$

Here, Q is the energy from one event of nuclear reaction; n ₁ and n ₂ are number densities as noted. V ₀ is the volume of a region with length l and radius r _L of the laser focusing area, and t _L is the duration of the laser pulse. This is a kind of inertial confinement fusion. ḄB. is a burning rate of the fuel. During the active reaction time, the density of fuel is varied as

$dn/dt = R_{\rm r} n_{0}^{2}$

and this can be written as

$1/n - 1/n_{0} = R_{\rm r} t_{0}.$

Here t ₀ is a characteristic time and is written as r _f/v _pe. v _pe is a perpendicular component of the plasma particle velocity in a focused area. In this case, the burning rate B is determined by

$B = \lpar n_{0} - n\rpar /n_{0}.$

Then, B is rewritten as

$B = Rt_{0} n_{0}/\lpar Rt_{0}n_{0} + 1\rpar \comma \;$

t ₀ is a confinement time of particles with cloud in the plasma. This equation indicates the burning rate and gives almost 1 by a simple estimation because the reaction rate is very large and the thermal velocity is very small.

Then, a gain of the energy G from the reactions is determined by

(12)

$G = \hbox{E}_{\,f}/\hbox{E}_{L}.$

E _L is the laser energy in t._L of one pulse and can be written as E_L = πr ²I t _L. When G is equal to 1.0, it is called break-even. Figure 9 shows the gain obtained from Eq. (12). In the case of Figure 9, the parameters used are summarized in Table 1. In the optimistic case, we can expect break-even at an almost 200 kJ laser, and we can obtain a gain of 10 for 1 MJ, although very high laser intensity with a 10 ps pulse is required. When we use the deuterium-deuterium reaction as a gain medium, hydrogen production by high temperature is possible in the reactor by this scheme (Imasaki & Lie, Reference Imasaki and Li2007).

Fig. 9. Nuclear reaction gain in this scheme.

6. CONCLUSION

In this article, the feasibility of a new approach of laser fusion for break-even of Deuterium plasma is discussed. We find out that the nuclear potential including mesons at the nuclear center plays an important role for tunneling of the Coulomb potential of the outer foot of the Coulomb barrier, which has not been expected before. The penetrability is significantly enhanced in this case. This penetrability leads to the sufficient nuclear reactions to obtain an energy gain by D-D reactions with a laser that power is around EW.

This is a primitive concept, so there are many issues to be solved as the relation of Coulomb barrier and energy level in three dimensions, the correct nucleon kinetic energy and so on. Further, the following problems have to be solved: (1) Saturation region on formation factor F. (2) Cloud behavior and life span. (3) Group velocity of nucleon and relative velocity of nucleon after tunneling. (4) Self-consistent field of Coulomb barrier region during the tunneling. These issues are under discussion.

ACKNOWLEDGEMENT

We sincerely thank Prof. C. Yamanaka for his helpful suggestion and comments on this model.

References

REFERENCES

Balantekin, A. & Takigawa, N. (1998). Quantum tunneling in nuclear fusion. Rev. Mod. Phys. 70, 77–100.CrossRef Google Scholar

Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–167.CrossRef Google Scholar

Bourdier, A., Patin, D. & Lefebvre, E. (2007). Stochastic heating in ultra high intensity laser-plasma interaction. Laser Part. Beams 25, 169–180.CrossRef Google Scholar

Deutsch, C. & Tahir, N. (2006). Fusion reactions and matter-antimatter annihilation for space propulsion. Laser Part. Beams 24, 605–616.CrossRef Google Scholar

Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRef Google Scholar

Hoffmann, D.H.H., Blazevic, A., Nt, P., Rosmei, O.M., Roth, M., Tahir, N.A., Tauschwitz, A., Udrea, S., Varentsov, D., Weyrich, K. & Maron, Y. (2005). Present and future perspectives for high energy density physics with intense heavy ion and laser beam. Laser Part. Beams 23, 47–53.CrossRef Google Scholar

Imasaki, K. & Li, D. (2007). An approach to hydrogen production by inertial fusion energy. Laser Part. Beams 25, 99–105.CrossRef Google Scholar

Imasaki, K. & Li, D. (2008). An approach of laser induced nuclear fusion. Laser Part. Beams 26, 3–7.CrossRef Google Scholar

Kuehl, T.H., Ursescu, D., Bagnoud, V., Javorkova, D., Rosmej, O., Cassou, K., Kazamias, S., Klisnick, A., Ros, D., Nickles, B., Zielbauer, B., Dunn, J., Neumayer, P., Pert, G. & the PHELIX Team. (2007). Optimization of the non-thermal incidence, transient pumped plasma X-ray laser for laser spectroscopy and plasma diagnostics at the facility for anti-proton and ion research (FAIR). Laser Part. Beams 25, 93–97.CrossRef Google Scholar

Kumar, A., Gupta, M.K. & Sharma, R.R. (2006). Effect of ultra intense laser pulse on the propagation of electron plasma wave in relativistic and ponderomotive regime and particle acceleration. Laser Part. Beams 24, 403–409.CrossRef Google Scholar

Li, D. & Imasaki, K. (2005). Vacuum laser-driven acceleration by a slit-truncated Bessel beam. Appl. Phys. Lett. 86, 031110.Google Scholar

Lifschitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser plasma accelerator. Laser Part. Beams 24, 255–259.CrossRef Google Scholar

Ostermeyer, M., Kong, H.J., Kovalev, V.I., Harrison, RG., Fotiadi, A.A., Megret, P., Kalal, M., Slezak, O., Yoon, J.W., Shin, J.S., Beak, D.H., Lee, S.K., Lu, Z., Wang, S., Lin, D., Knight, J.C., Kotova, N.E., Straber, A., Scheikh-Obeid, A., Riesbeck, T., Meister, S., Eichler, H.J., Wang, Y., He, W., Yoshida, H., Fujita, H., Nakatsuka, M., Hatae, T., Park, H., Lim, C., Omatsu, T., Nawata, K., Shiba, N., Antipov, O.L., Kuznetsov, M.S., Zakharov, N.G., Patin, D., Lefebvre, E., Bourdier, A. & D'Humieres, E. (2006). Stochastic heating in ultra high intensity laser-plasma interaction: Theory and PIC code simulations. Laser Part. Beams 24, 223–230.Google Scholar

Sakai, K., Miyazaki, S., Kawata, S., Hasumi, S. & Kikuchi, T. (2006). High-energy-density attosecond electron beam production by intense short-pulse laser with a plasma separator. Laser Part. Beams 24, 321–327.CrossRef Google Scholar

Sherlock, M., Bell, A.R. & Rozmus, W. (2006). Absorption of ultra-short laser pulses and particle transport in dense targets. Laser Part. Beams 24, 231–234.CrossRef Google Scholar

Shimada, Y., Nisimura, H., Nakai, M. & Yamanaka, C. (2005). Characterization of extreme ultraviolet emission from laser produced spherical tin plasma generated with multiple laser beams. Appl. Phys. Lett. 86, 051501.CrossRef Google Scholar