Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T10:26:24.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast ignition of fusion pellets with superintense lasers: Concepts, problems, and prospectives

Published online by Cambridge University Press:  01 March 2004

P. MULSER  and
D. BAUER
P. MULSER
Affiliation:
Theoretical Quantum Electronics (TQE), Darmstadt University of Technology, Darmstadt, Germany
D. BAUER
Affiliation:
Theoretical Quantum Electronics (TQE), Darmstadt University of Technology, Darmstadt, Germany
Rights & Permissions [Opens in a new window]

Abstract

The concept of fast ignition of precompressed pellets for inertial confinement fusion is presented and the main approaches are discussed. Numerical simulations of fast coronal ignition and the peculiarities of this scheme are considered in detail. Particular attention is devoted to the energy transport in the pellet corona. It is shown that fast coronal ignition will be successful only if the energy deposition by the fast electrons is anomalous over a sufficiently extended overdense region. Alternative schemes are briefly discussed.

Keywords

Energy transportFast ignitionSuperintense lasersThermonuclear burn
Type
International Conference on the Frontiers of Plasma Physics and Technology
Information
Laser and Particle Beams , Volume 22 , Issue 1 , March 2004 , pp. 5 - 12
Copyright
2004 Cambridge University Press

1. INTRODUCTION

The concept of fast external ignition of deuterium–tritium (DT) fuel by a superintense laser pulse to initiate thermonuclear burn dates back to an idea of M. Tabak in 1994. Since then it has attracted vivid interest owing to the new prospects it opens in the field of inertial confinement fusion (ICF) with lasers and heavy ion beams (Lindl, 1995). ICF is the alternative to magnetic confinement fusion, the two routes to controlled fusion energy gain.

In contrast to standard central ignition by a converging shock wave (Lindl, 1995; Kemp et al., 2001), fast ignition (FI) consists in heating a portion of the precompressed DT pellet to temperatures above 6 keV during the time of 10–30 ps by a laser beam of at least 1019 W/cm2 intensity (Tabak et al., 1994). During the last 8 years, the concept of FI has evolved theoretically and, at the same time, has stimulated preparatory experiments in leading high power laser laboratories (Lawrence Livermore National Laboratory [LLNL], Livermore, Institute of Laser Engineering (ILE) Osaka, Rutherford-Appleton Laboratory (RAL) Tilton, Laboratoire Utilisation des Lasers Intense (LULI) Palaiseau, Max Planck Institute of Quantum Optics (MPQ) Garching). Currently we may distinguish three FI approaches, differing from each other:

  • Fast beam ignition (FBI): fast heating of compressed DT by laser-generated intense electron beams or electron “spray” (Tabak et al., 1994) or by intense secondary proton (or ion) beams (Roth et al., 2001; Atzeni, 1999);
  • Cone-guided fast ignition (CFI): laser energy input and eventual secondary products are guided and concentrated by a cone of a high-Z material in the fusion pellet (Kodama et al., 2001, 2002);
  • Fast coronal ignition (FCI): ignition starts from a sufficiently dense part of the outer corona and propagates like a bushfire over the precompressed pellet (Hain & Mulser, 2001a).

According to first studies, the fast ignition approach offers several advantages:

  • separation of the pellet ignition from its compression phase,
  • largely insensitive to mass distribution and compression asymmetries,
  • widely safe against Rayleigh–Taylor growth,
  • high burn efficiency.

A successful proof of the scientific feasibility of FI will have a major impact on future ICF pellet design, in particular, perhaps already on National Ignition Facility (NIF) (Campbell & Hogan, 2000), on Laser Mega Joule Project (LMJ) (André, 2000), and on ICF in general, for example, on the decision direct versus indirect drive (Lindl, 1995).

The feasibility of FI stands and falls with the possibility to effectively absorb the laser energy in the underdense corona (first deposition zone), and then to transport it to pellet regions of sufficient density (second deposition zone) to initiate a self-sustained burn wave (Fig. 1).

Fast coronal ignition (FCI) scheme. Hot electrons provide for the necessary energy transport from the first to the second energy deposition zone.

Experimental and theoretical studies carried out so far have shown that in the underdense corona, an extremely hot plasma is generated and that no laser light can propagate beyond the (relativistically increased) critical density. On the other hand, to initiate a self-sustained burn wave, certain requirements for the product of density and dimensions of the heated matter must be fulfilled (modified ρR or equivalently nτ Lawson criterion; Lindl, 1995). Therefore energy transport is the key issue in studying fast ignition. It is well known that at a moderate supply of energy, the transport occurs by thermal diffusion. Under conditions of FI, coronal heating occurs so violently that the plasma is nonthermal in a strict sense: Intense jets of relativistic electrons and multimegaGauss magnetic fields are generated that lead to self-pinched collimated filaments, to their collapse, and to violent (field) energy bursts by the phenomenon of magnetic reconnection. These questions arise: (1) by which mechanisms, (2) how much energy can be transported, and (3) where, that is, at which density, is it deposited? This is terra incognita, a complex subject of basic research and a widely unexplored territory. Which FI scheme will be the winner depends on the answer to question (3). Deposition at high density favors FBI, deposition in a medium density region makes CFI perhaps more attractive, whereas FCI starts working when matter of approximately 5 gcm−3 density is heated above 6 keV.

The formation of highly relativistic collimated electron jets by superintense laser irradiation, their eventual conversion into well-focused proton or ion beams, observed in simulations and experiments and, finally, the question of how much and by which mechanisms energy can be transported from one region of space to another have their own fascination and link laboratory physics to an exciting phenomenon of modern astrophysics: It is a widely diffused belief that the coronal jets and the collimated cosmic jets have much physics in common (Schopper et al., 1999).

The energy transport problem is closely connected with essential issues of superintense laser–matter interaction, for example, laser beam propagation through the low-density plasma corona up to the critical density surface (refractive index is zero) where both strong absorption and reflection may occur. The spectrum of the relativistically accelerated electrons depends sensitively on the mechanisms of absorption in the corona and in the critical region, which, in turn, causes the formation of collimated jets and decides the leading energy transport mechanism and its efficiency. A feasibility study of fast ignition is largely identical with the investigation of electron jet formation and/or energy transport, depending on whether FBI or FCI is faced. With FI another, totally new, aspect comes into play: All superintense laser–matter studies so far were undertaken in the 1 kJ, 10 fs–1 ps domain; FI must work in the multipicosecond (typically 30 ps) and multikilojoule domain.

From the point of view of pure science and of application, fast ignition is a research subject of pioneering significance. From its solution spinoffs will emerge that may largely justify already the common effort in the field. Finally, first investigations performed give rise to moderate optimism for FI.

This article is organized as follows. First a brief overview is given of superintense laser–subcritical plasma interaction, with particular emphasis on absorption. Then the concept of FCI and simulations of it are presented. In the following section, the most sensitive aspect, that is, the energy transport from the first to the second deposition zone is analyzed. It is very likely that FI will work at reasonable parameters only under the condition that the interzone energy transport is anomalous, that is, not diffusive. Finally, a brief consideration is devoted to FBI and CFI, followed by concluding remarks.

2. LASER BEAM PROPAGATION AND ENERGY DEPOSITION

The concept of FI applies to a fusion pellet that is precompressed by a nanosecond laser in the megajoule energy range. The compression is done directly or indirectly along a low temperature adiabate to reach typical densities of 300 to 400 gcm−3, corresponding to 1500–2000 times the solid density of a 1:1 DT mixture. The high-density pellet core is surrounded by a hot, fully ionized low-density corona. The superintense short pulse FI laser expels the coronal plasma along its path by thermal and ponderomotive pressures and penetrates up to the critical density. From there it cannot propagate further because the refractive index assumes imaginary values. This is also true for relativistic laser intensities, as shown by all computer simulations performed so far. The simulations presented in this section are performed at a Nd laser wavelength of 1060 nm and critical density nc = 1021 cm−3. If not stated differently, all the following estimates are based on the Ti:Saphire laser of 800 nm wavelength and ωTi:Sa = 2.35 × 1015 s−1 frequency, corresponding to a critical electron density of ne = 1.8 × 1021 cm−3. As a consequence, at such a low density cutoff, collisional absorption becomes totally insignificant and, in concomitance, two questions arise: Is the beam propagation in the underdense corona seriously inhibited by parametric instabilities and, if not, which are the effective absorption mechanisms in the critical region?

Standard analysis of the familiar parametric instabilities shows very fast growth of Raman and Brillouin back- and sidescattering at the leading edge of the laser pulse, followed by drastic depletion on the picosecond time scale (Quesnel et al., 1997a,b). Direct insight into parametric growth and beam transmission is gained from a fully relativistic one-dimensional Maxwell–Vlasov kinetic and two-dimensional (2D) Maxwell hydrosimulations (Hain, 1999; Hain & Mulser, 1999). They clearly show that at intensities higher than 1018 Wcm−2, parasitic effects saturate at a level of, at most, 10% after 100 fs (Fig. 2). In an experiment, a Raman backscattering level of less than 3% was found (Miyakoshi et al., 2002).

Two-fluid simulation of laser beam–plasma interaction (Raman instability), a: Transverse electric field Ey (units 3 × 1010 Vcm−1; dashed line) and electron density ne (units 1021 cm−3; solid line); nc = 4. The laser intensity is 1.6 × 1018 Wcm−2. The electron spikes indicate that the excited wave is strongly nonlinear but not yet broken. b: Electron density ne (solid line) and Poynting flux Sx in units of 2.45 × 1018 Wcm−2. The laser intensity is 1019Wcm−2. Irregular structure of ne is due to wavebreaking. Reflection is less than 10%. x is in units of Nd laser wavelength λ = 1.06 μm.

The physical explanation is very simple. As soon as there is an appreciable electron density modulation created, spontaneously or by ponderomotive effects, the light pressure blows it off. Absorption of the laser beam is confined to a narrow zone around the critical surface. At high intensities, the plasma density profile is steepened by light pressure to a fraction of a laser wavelength. The v × B force at normal incidence and the electric laser field component perpendicular to the critical surface lead to breaking of the induced electron density modulations, which, in turn, through Poisson's equation, excite collective electric fields out of phase. As a consequence, a nonzero contribution to the cycle-averaged jE term of Poynting's theorem appears. Fully relativistic Maxwell–Vlasov kinetic simulations confirm this picture of collective absorption (Ruhl & Mulser, 1995). Maximum absorption in plane targets amounts to about 60%. Its angular dependence is very sensitive to L. As soon as it is such that a plasma oscillation can build up, say half an electron plasma wavelength, the familiar resonance absorption takes place with high efficiency. With the intensity growing from I = 1017 to I = 1018 Wcm−2, the absorption decreases owing to the formation of a static electron accumulation in front of the critical surface, which causes an unfavorable phase shift of the oscillating longitudinal electric field. Such a decrease of absorption is not observed in experiments; furthermore, at large angles of incidence absorption up to 80% was measured at I = IO19 Wcm−2 (Feurer et al., 1997). The apparent contradiction disappears if one keeps in mind that at high irradiances the flat target surface is curved and/or corrugated by the light pressure (Macchi et al., 2001). In Figure 3, a 2D particle-in-cell (PIC) simulation (Ruhl et al., 1999; 1.5 × 107 particles) of deformed targets is shown (deformation parameter δ; Fig. 3a).

2D PIC simulation of deformed targets, a: Electron density ne, normalized to nc for δ = 1 μm at t = 0 fs. The dashed line shows the density along y = 5 μm (scale on RHS axis), b–d: The fractional absorption A versus time (b) as a function of δ for Iλ2 = 4.0 × 1018 Wcm−2 μm2 and ne /nc = 15.0, (c) as a function of Iλ2 in units of 1018 Wcm−2 μm2 for δ = 1 μm and ne /nc = 15.0, and (d) as a function of ne /nc for Iλ2 = 4.0 × 1018 Wcm−2 μm2 and δ = 1 μm.

In Figure 3b, the net absorption as a function of time is presented for three different values of δ showing its monotonous increase up to 80% at δ = 2 μm and normal incidence. The plots of Figure 3c,d show that the collective (collisionless) absorption tends to saturate for Iλ2 > 1.5 × 1018 Wcm−2 μm2. Lowering of A with ne /nc increasing is a consequence of reducing skin length (Fig. 3d). In summary, it is realistic to assume that at high irradiances, the absorption is not less than 50%.

3. FAST CORONAL IGNITION (FCI)

Because the laser energy cannot be absorbed at a higher than critical density, fast thermonuclear ignition of the pellet must start from a suitable density somewhere in the corona, unless processes can be found by which almost all laser beam energy is converted into beams of highly energetic heavy particles or electrons. This latter possibility is discussed later. Here we concentrate on (1) what amount of thermal energy and energy flux density must be supplied during 10 to 30 ps to the second deposition zone and (2) at which minimum density must this region be located in order to lead to ignition of the precompressed pellet core by diffusive electron energy transport. This concept of FCI was presented first by Hain and Mulser (2001a) and has been more elaborated meanwhile.

To investigate the feasibility of this scheme we performed burn simulations in cylindrical geometry (coordinates x,r) by the use of a 2D Yabe-type hydrocode (Yabe et al., 1991; Tanaka et al., 2000), which incorporates electronic heat conduction (flux-limited Spitzer, qmax = kTe(2kTe /πme)1/2ne), diffusive mass and energy transport of α particles (Atzeni-Caruso model; Atzeni et al., 1981; Atzeni, 2000), and volume emission of bremsstrahlung. Nuclear burn is calculated in a three-temperature model for electrons, ions, and α particles. The use of a separate α particle temperature Tα is essential. The original energy input is to the electrons; from there it flows to the ions. The burn front is triggered by electronic heat conduction and α particle diffusion. Finally, the reaction energy is transmitted to the electrons to sustain burn. The simulations were performed with compressed shells and full spheres of 2–5 mg mass and peak densities ranging from 300 to 500 gcm−3 and energies up to several tens of kilojules deposited during 20 ps. For ignition to be successful, energy flux densities above 1020 Wcm−2 had to be chosen in all numerical runs. As a specific example, a 5-mg DT shell is taken that is compressed along a low adiabate by a nanosecond laser pulse until it stagnates in the center and a maximum density of 350 gcm−3 is reached on a concentric shell. The mass concentration assumes a doughnut-like shape as presented by the density contour plot in Figure 4 (Hain & Mulser, 2001b).

Fast ignition and burn of a precompressed 5-mg DT shell 73 ps after the end of the laser pulse. Laser intensity I = 1021 Wcm−2 over τ = 20 ps; 75 kJ energy deposited at ρ = 4.6 gcm−3 (outer contour); beam radius r = 11 μm, ρmax = 350 gcm3 electron heat transport by flux-limited Spitzer diffusion. Instead, “free ignition energy” is 15 kJ. High burn efficiency (25%).

To achieve ignition by flux limited Spitzer heat transport, the density of the deposition zone should not be less than 4–5 gcm−3 DT. Below 1 gcm−3 in no run a burn wave evolved. In the example here, deposition occurred at ρ = 4.6 gcm−3 (outer contour in the picture). The evolving shock (nonspherical black region) is driven by the heat wave and the thermonuclear deflagration wave, and is not connected with the phenomenon of hole boring. Owing to Spitzer flux limitation, most of the energy of 75 kJ supplied to the pellet is dispersed in the lower density corona. Nonetheless the overall burn efficiency is as high as 25%. To find out which portion of energy drives the FCI process (named here “free ignition energy” and “free ignition intensity”) the same simulation is done without flux limitation. In this way a free ignition energy and intensity of 15 kJ and 2 × 1020 Wcm−2 were found. From various other computer runs with compressed shells, similar figures were extracted, with energy inputs not lower than 50 kJ. Perhaps with systematic optimization of parameters and pellet design for FCI this figure can be lowered in a next stage of simulations. So, for example, it has been found that exact timing of the heating pulse during the compression phase led to remarkable burn efficiency improvements (Hain & Mulser, 2001a).

In the left upper corner in Figure 4 the fraction of burned fuel of 1.3% at the instant of 73 ps is indicated. After 23 ps, when the energy input had already stopped, only the fraction of 10−4 DT fuel has reacted and violent combustion sets in not before 80 ps. This is because the heat wave/shock front takes much time to propagate into regions of high density. The ρR parameter never exceeds the approximate value of 3 gcm−2. In order not to waste precious ignition energy, it is essential that the shock in front of the heat wave must not decouple from the heat front, because, with the energies under consideration, the generated shock is not strong enough to induce burn without the support of the electron heat wave. The influence of asymmetry on FCI was studied with full spheres exhibiting maximum compression shifted by a half radius from the center with the consequence that the burn degraded from 6.5% (centered) to 6.0% (shift away from deposition) and to 5.4% (shift toward deposition). The burn efficiency can also be increased by using energy input from two opposite beams; however, the effect remains modest owing to lateral cold fuel expulsion by the colliding burn fronts.

3.1. Consistency consideration

The maximum nonrelativistic heat flux density qmax for a thermal electron distribution is given by

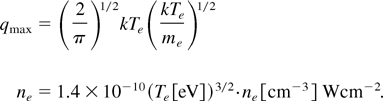
Setting qmax = 1021 Wcm−2, and ne = 1.15 × 1024 cm−3 corresponding to ρ = 4.6 gcm−3, the lower limit for the electron temperature Te = 34 keV results. This is much lower than Te = 150 keV from the simulation. The electron–ion frequency at this latter temperature and the density ne = 1.15 × 1024 cm−3 amounts to vei = 9 × 1012 s−1. Thus, a model based on thermal equilibrium and diffusive energy transport is compatible as soon as the density in the second deposition zone reaches 4 gcm−3.

4. THE FIRST DEPOSITION REGION AND ANOMALOUS TRANSPORT

Owing to radiation pressure, the corona density profile is steepened and energy absorption takes place in a very narrow zone around the the critical surface. At the intensities under consideration, the oscillatory motion of the electrons is highly relativistic. There is no simple model available so far that is able to explain the collective absorption process, that is, how the regular motion induced by the electric field is converted into irreversible internal energy. There have been proposed several models in the past—Brunel effect (Brunel, 1987, 1988), j × B heating (Kruer & Estabrook, 1985), dephasing by symmetry breaking (Mulser et al., 2001)—that shed light on particular aspects of heating; however, none of them is able to describe the spectra of fast electrons observed in experiments and simulations. Nevertheless, from all of them, and especially from simulations, one can extract a qualitative aspect: collective, that is, collisionless absorption, or irreversibility is induced by wavebreaking. In the present case it means breaking of the regular motion by mixing of fluid elements. For fast ignition studies it is essential that absorption is efficient. In fact, kinetic temperatures are generated of the order of the mean oscillation energies. As a consequence, the critical density is upshifted toward higher densities. The relativistic shift is determined from the Fourier coefficient of the fundamental electric current component j1 oscillating at the laser frequency ω. With the thermal energy Eth and by making use of the conservation of the canonical momentum along the laser field one finds

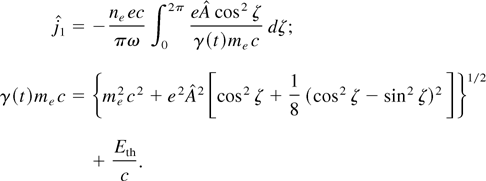
In the ultrarelativistic case, of relevance in our context, from the wave equation for the ω component of E, the approximate expression for the relativistic critical density ncrel is obtained:

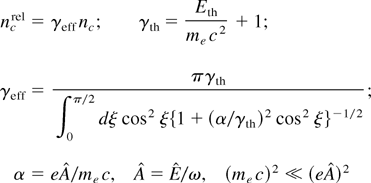
It is well known that for a circularly polarized wave

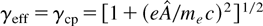
. For a linearly polarized wave in a cold medium Eq. (3) yields γeff = 0.8γcp. For the following considerations, intensities I = 1020 and 1021 Wcm−2 and

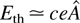
Ti:Sa are of relevance. The corresponding values of γeff are obtained from γeff = 1.2γcp. The resulting parameters are presented in Table 1 for Ti:Sa and KrF.

Relativistic increase of the critical density nC by the factor γeff at high laser intensities I with laser frequency

In Section 2 we found the heat flux density needed to ignite the pellet qth = 1021 Wcm−2. It cannot be assumed that the energy flux converges along its passage from the first to the second deposition zone (there is rather a tendency to diverge). Hence, I = ncrelcEth/2 ≥ qth is a conservative necessary condition on Eth. Thus, the average thermal energy per electron amounts to Eth = 9.1 MeV; the concomitant mean oscillation energy Eos = 7.3 MeV for Ti:Sa frequency. Should no flux limiter be necessary for some reason or another, the free ignition flux density is 2 × 1020 Wcm−2 and Eth and Eos still become as high as 4.2 MeV and 6.0 MeV. Such energetic electrons cannot be effectively stopped by the compressed pellet, neither in one, nor in the other case. It cannot be excluded that the relevant electron density ne at which absorption occurs is lower than ncrel and I > qth. Then Eth and Eos are even higher. The unavoidable conclusion therefore is that only if the energy deposition by the fast electrons in the region ne > ncrel is anomalous is there a chance for fast coronal ignition to work at Ti:Sa laser wavelength. The required laser pulse energy thereby lowers with the second deposition zone shifting toward higher densities. For KrF laser wavelengths the constraints look less severe.

4.1. Indications of anomalous transport

The coronal energy flow towards the second deposition region is necessarily accompanied by electric charge flows of energetic electrons. As a consequence, a return current of overall equal strength must flow toward the critical region in order to maintain quasineutrality in the plasma. Such a flow topology is unstable with respect to the electrostatic two-stream, tearing, and the magnetic pinch or filamentary instability. In numerical simulations, the formation of filaments was observed and it was also observed that their dynamics in two and three dimensions differ substantially, which means that the phenomenon is a three-dimensional (3D) effect (Ruhl, 2002; Sentoku et al., 2002). The filaments start developing at the critical surface and extend over considerable lengths; their diameter is of the order of the laser wavelength. Pinching is accomplished by magnetic fields of several hundreds of megaGauss. These strong fields lead to heavy lateral particle losses of the slower electrons undergoing gyrations of the order of the filament diameter. Only the fast electrons of megaelectron volt energies survive and transport a significant fraction of the laser energy deep into the higher density corona. The analysis of the associated fields shows that highly magnetized transport takes place and that the electrostatic fields are of minor significance. Although the current in a filament can exceed the Alfven limit (Lawson, 1958) up to 10 times (Ruhl, 2002) or more (Sentoku et al., 2002), magnetic filamentation severely inhibits the ballistic energy flow given by qe = neEthc. This is bad news for FCI. However, the simulations could be performed at a maximum particle density of ne = 3.33 × 1022 cm−3 (overall CPU time 29.000 hours; Ruhl, 2002). Another series of PIC simulations close to solid density with collisions included led instead to anomalously increased electron energy deposition in the overdense corona for which no physical explanation exists at present (H. Ruhl, pers. comm.). On the other hand, anomalous stopping of intense electron beams is very likely to occur since, as all 3D PIC simulations show, they interact with the dense plasma by a whole variety of collective processes. Recently, Kaw, Das, and Jain (2002) investigated the role of sausage and kink instabilities and were able to show that electron magnetohydrodynamic turbulence excited by fast electron currents may play an important role in collective stopping. The research of anomalous electron transport under FI conditions is just at its beginning. Finally, stopping may be enhanced by collective Coulomb interaction analogous to enhanced collisionality in an extended cluster medium (P. Mulser, 2003).

5. ALTERNATIVES TO FCI: FAST BEAM IGNITION (FBI) AND CONE-GUIDED FAST IGNITION (CFI)

When the fast electrons surviving magnetic deflection leave the rear surface of a solid target, a strong electric field is generated in which protons (or light ions) are collectively accelerated to multimegaelectron volt energies and form extremely short and intense particle bunches that may be used to ignite precompressed pellets (Roth et al., 2001). Subsequent studies have shown the tolerable intervals for particle energy, beam power, and beam intensity and have fixed a threshold proton energy input of 14 kJ (Piriz & Sanchez, 1998) and 40 kJ (Atzeni et al., 2002). FBI has many inherent advantages. Its success will depend on the efficiency with which energetic proton or light ion bunches can be produced in the future. At present the conversion rate is very low. CFI has been shown to be a successful scheme at laboratory energies (typically ≤1 kJ): It leads to better laser beam focusing, increased absorption, and brings the first absorption zone closer to the dense pellet core. At realistic ignition energies, however (>50 kJ), the scheme is expected not to differ substantially from FCI and similar or additional complications may arise: The cone may fill up with plasma, with concomitant strong energy diffusion to the outer corona; there may be detrimental addition of 40 mg high-Z material (risk of nuclear activation) to the small DT mass of about 5 mg only; alternatively, increased ponderomotive profile steepening may lead to skin layer narrowing and decrease of absorption. Besides this, it adds a nonignorable technical complication.

6. CONCLUSIONS

Fast ignition is an appealing concept of inertial confinement fusion research and its various schemes, which, at closer inspection, essentially reduce to two and offer considerable advantages in comparison to central spark ignition. In particular, the study presented on FCI may be summarized as follows: Minimum density for energy deposition is 4–5 gcm−3; below 1 gcm−3 no ignition is possible with reasonable energy input (E ≤ 100 kJ; minimum energy supplied here was 50 kJ; minimum energy flux density qe = 1021 Wcm−2, minimum temperature Te = 100 keV; “free ignition energy” > 8 kJ, “free” qe ≥ 2 × 1020 Wcm−2. Most energy supplied is dispersed in the low-density corona; ignition is retarded owing to finite heat wave propagation; shock induced must not decouple from the heat wave front; burn efficiency is high (25%); insensitivity to pellet asymmetries. Symmetrized illumination by two beams brings little advantage (1%). At present it is premature to make predictions on its real chances because in the case of FCI, the widely unexplored mechanisms of energy transport will decide its success whereas FBI will be successful only if the conversion of laser energy into particle beam energy can be substantially increased. In both cases, a great amount of novel and basic nonlinear physics on transport has to be understood first.

ACKNOWLEDGMENT

Useful discussions with Prof. F. Cornolti from Pisa University are gratefully acknowledged.

References

REFERENCES

André, L.M. (2000). Laser megajoule project status. In Inertial Fusion Sciences and Applications (Labaune, Ch., Hogan, W.J. & Tanaka, K.A., Eds.) Paris: Elsevier, p. 32.
Atzeni, S. (1999). Phys. Plasmas 6, 3316.
Atzeni, S. (2000). In Inertial Fusion Sciences and Applications, (Labaune, Ch., Hogan, W.J. & Tanaka, K.A., Eds.) Paris: Elsevier, p. 415.
Atzeni, S., Caruso, A. & Pais, V.A. (1981). Nuovo Comento 64, 383.
Atzeni, S., Temporal, M. & Honrubia, J.J. (2002). Nucl. Fusion 42, L1.
Brunel, F. (1987). Phys. Rev. Lett. 59, 52.CrossRef
Brunel, F. (1988). Phys. Fluids 31, 2714.
Campbell, E.M. & Hogan, W.J. (2000). In Inertial Fusion Sciences and Applications (Labaune, Ch, Hogan, W.J. & Tanaka, K.A., Eds.) Paris: Elsevier, p. 9.
Feurer, T., Theobald, W., Sauerbrey, R., Uschmann, I., Altenbernd, D., Teubner, U., Gibbon, P., Förster, E., Malka, G. & Miquel, J.L. (1997). Phy. Rev. E 56, 4608.
Hain, S. (1999). Propagation of Intense Laser Radiation through Matter. Herdecke, Germany: GCA-Verlag (in German).
Hain, S. & Mulser, P. (1999). GSI-99-04 Report, Gesellschaft für Schwerionenforschung, Darwstadt.
Hain, S. & Mulser, P. (2001a). Phys Rev. Lett. 86, 1015.
Hain, S. & Mulser, P. (2001b). High Energy Density in Matter Produced by Heavy Ion Beams, GSI-2001-4 Report, Gesellschaft für Schwerionenforschung, Darwstadt.
Kaw, P.K., Das, A. & Jain, N. (2002). Proc. International Conf on the Frontiers of Plasma Physics and Technology. National Research Institute for Applied Mathematics, Bangalore, India, p. 12.
Kemp, A., Meyer-ter-Vehn, J. & Atzeni, S. (2001). Phys Rev. Lett. 86, 3336.CrossRef
Kodama, R., Norreys, P.A., Mima, K., Dangor, A. E., Evans, R.G., Fujita, H., Kitagawa, Y., Krushelnick, K., Miyakoshi, T., Miyanaga, N., Norimatsu, T., Rose, S.J., Shozaki, T. Shigemori, K., Sunahara, A., Tampo, M., Tanaka, K.A., Toyama, Y., Yamanaka, T., &Zepf, M. (2001) Nature 412, 798.
Kodama, R., Shiraga, H., Shigemori, K., Toyama, Y., Fujioka, S., Azechi, H. Fujita, H., Habara, H., Hall, T., Izawa, Y., Jitsuno, T., Kitagawa, Y., Krushelnck, K.M., Lancaster, K.L., Mima, K., Nagai, K., Nakai, M., Nishimura, H., Norimatsu, T. Norreys, P.A., Sakabe, S., Tanaka, K.A., Youssef, A., Zepf, M. & Yamanaka, T. (2002). Nature 418, 933.
Kruer, W.L. & Estabrook, K. (1985). Phys. Fluids 28, 430.
Lawson, J.D. (1958). J. Electron. Control 5, 146.
Lindl, J. (1995). Phys. Plasmas 2, 3933.
Macchi, A., Cornolti, F., Pegoraro, F., Liseikina, T.V., Ruhl, H. & Vshivkov, V.A. (2001). Phys. Rev. Lett. 87, 205004.CrossRef
Miyakoshi, T., Jovanović, M.S., Kitagawa, Y., Kodama, R., Mima, K., Offenberger, A.A., Tanaka, K.A. & Yamanaka, T. (2002). Phys. Plasmas 9, 3552.
Mulser, P. (2003). Contrib. Plasma Phys. 43, 330.CrossRef
Mulser, P., Ruhl, H. & Steinmetz, J. (2001). Laser Part. Beams 19, 23.
Piriz, A.R. & Sanchez, M.M. (1998). Phys. Plasmas 5, 4373.
Quesnel, B., Mora, P. & Adam, J.-C. (1997a). Phys. Rev. Lett. 18, 2132.
Quesnel, B., Mora, P. & Adam, J.-C. (1997b). Phys. Plasmas 4, 3358.
Roth, M., Cowan, T.E., Brown, C., Christl, M., Fountain, W., Hat chett, S., Johnson, J., Key, M.H., Pennington, D.M., Perry, M.D., Philips, T.W., Sangster, T.C., Singh, M., Snavely, R., Stoyer, M., Takahashi, Y., Wilks, S.C. & Yasuike, K. (2001). Phys. Rev. Lett. 86, 436.CrossRef
Ruhl, H. (2002). Plasma Sources Sci. Technol. 11, A1, A5.
Ruhl, H., Macchi, A., Mulser, P., Cornolti, F. & Hain, S. (1999). Phys. Rev. Lett. 82, 2095.CrossRef
Ruhl, H. & Mulser, P. (1995). Phys. Lett. A 205, 388.
Schopper, R., Birk, G.T. & Lesch, H. (1999). Phys. Plasmas 6, 4318.
Sentoku, Y., Mima, K. & Sheng, Z.M. (2002). Phys. Rev. E 65, 046408.
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M. & Perry, M.D. (1994). Phys. Plasmas 1, 1626.
Yabe, T., Ishikawa, T., Wang, P.Y., Aoki, T., Kodata, Y. & Ikeda, F. (1991). Comput. Phys. Commun. 66, 233.CrossRef
Figure 0

Fast coronal ignition (FCI) scheme. Hot electrons provide for the necessary energy transport from the first to the second energy deposition zone.

Figure 1

Two-fluid simulation of laser beam–plasma interaction (Raman instability), a: Transverse electric field Ey (units 3 × 1010 Vcm−1; dashed line) and electron density ne (units 1021 cm−3; solid line); nc = 4. The laser intensity is 1.6 × 1018 Wcm−2. The electron spikes indicate that the excited wave is strongly nonlinear but not yet broken. b: Electron density ne (solid line) and Poynting flux Sx in units of 2.45 × 1018 Wcm−2. The laser intensity is 1019Wcm−2. Irregular structure of ne is due to wavebreaking. Reflection is less than 10%. x is in units of Nd laser wavelength λ = 1.06 μm.

Figure 2

2D PIC simulation of deformed targets, a: Electron density ne, normalized to nc for δ = 1 μm at t = 0 fs. The dashed line shows the density along y = 5 μm (scale on RHS axis), b–d: The fractional absorption A versus time (b) as a function of δ for Iλ2 = 4.0 × 1018 Wcm−2 μm2 and ne /nc = 15.0, (c) as a function of Iλ2 in units of 1018 Wcm−2 μm2 for δ = 1 μm and ne /nc = 15.0, and (d) as a function of ne /nc for Iλ2 = 4.0 × 1018 Wcm−2 μm2 and δ = 1 μm.

Figure 3

Fast ignition and burn of a precompressed 5-mg DT shell 73 ps after the end of the laser pulse. Laser intensity I = 1021 Wcm−2 over τ = 20 ps; 75 kJ energy deposited at ρ = 4.6 gcm−3 (outer contour); beam radius r = 11 μm, ρmax = 350 gcm3 electron heat transport by flux-limited Spitzer diffusion. Instead, “free ignition energy” is 15 kJ. High burn efficiency (25%).

Figure 4

Relativistic increase of the critical density nC by the factor γeff at high laser intensities I with laser frequency