Published online by Cambridge University Press: 25 March 2004
A commercial mode locked cavity dumped Nd:YAG dye laser operating at 10 Hz repetition rate is modified to produce a high contrast (>5000:1) single laser pulse while maintaining the energy stability and high beam quality. A trigger generator biases the cavity dumping photodiode, which is triggered externally by a pulse from the microprocessor-based control unit controlling a ∼2 J/200 ps laser chain. In the laser chain, the high contrast (>5000:1) is achieved by an external pulse selector based on single Pockel's cell to select a single laser pulse of high contrast, which is a prerequisite for experimental study of the equation of state. Laser-induced shock velocity measurement in thin aluminum, gold on aluminum, and copper on aluminum foil targets using this modified laser system are also presented. The equation of state of Al, Au, and Cu obtained using an impedance matching technique are in agreement with the reported results of SESAME and simulation results.
High power neodymium lasers available today with a peak power of hundreds of gigawatts find their use in laser plasma interaction studies, laser material processing, nonlinear studies, X-ray lasers, laser-induced ablation of material, and so forth. Usually lasers required to conduct such studies consist of a master oscillator delivering a low energy (few millijoules) laser pulse of a duration ranging from nanosecond to picosecond, which is followed by set of amplifiers and Faraday isolator to boost the laser energy from the laser oscillator to the desired level. The laser chain that involves a commercial oscillator and a series of amplifiers in master oscillator power amplifier (MOPA) configuration offers high-energy stability, reliability, and design flexibility (Koechner, 1992). However for stable operation, these oscillators are operated at a frequency ranging from 1 to 10 Hz. The high repetition rate operation of the oscillator takes care of thermal lensing in YAG rods, whereas external amplifiers and a Faraday isolator are operated in the single-shot mode. The typical commercial oscillator operating at 10 Hz in the laser chain delivers an output consisting of some prepulses and the main laser pulse with a contrast ratio of ∼50:1. The experiments involving laser-induced ablation of material or laser–plasma interaction require a single, high contrast (>1000:1), clean, high-power laser pulse. In this article, we present the design details of a 2 J/200 ps laser chain that involves a modified commercial oscillator for single-shot operation by pulsed biasing of the cavity dumping photodiode, external pulse selector based on a single Pockel's cell used in push–pull configuration between two crossed polarizers, two silicate glass amplifiers, and a Faraday isolator.
The equation of state (EOS) of a material under high-pressure conditions is important to several branches of physics, in particular, astrophysics, materials science, and inertial confinement fusion research (Lindl, 1995; Celliers et al., 2000). EOS data (Chidambaram, 1996; Sikka et al., 1997) is also important for simulation of fission and fusion devices. Several techniques are available for generating shock pressures ranging from 1 Mbar to hundreds of megabars. Diamond anvil cell and two-stage gas gun can produce shock pressures up to 5 and 10 Mbar, respectively (Nellis et al., 1988; Mitchell et al., 1991). Shock pressures greater than 10 Mbar can be obtained in underground nuclear tests that are difficult to perform (Trunin et al., 1969). High-power pulsed lasers offer new ways of producing shock pressures of more than a few tens of megabars (Trainor et al., 1979; Veeser et al., 1979; Ng et al., 1985). A high-power laser pulse focused on a thin foil target (a few microns) kept in vacuum with irradiation intensity ≥1014 W/cm2 creates a high-density, high-temperature ablating plasma at the front surface that launches a dynamic shock inside the material. The shock wave propagates in the target material and, on unloading at the rear surface, generates a visible optical emission. The shock transit time in the material measured with a high-speed streak camera gives the shock velocity. Recent laser-driven shock wave experiments have demonstrated high-quality planar shock waves induced by thermal radiation from a hohlraum cavity with measured pressures as high as 750 Mbar (Cauble et al., 1993; Lower et al., 1994). However, in all published work on laser-driven shock wave experiments, the pressure has been determined indirectly from the measurement of the shock velocity with the use of known EOS of a reference material. Direct measurement of the EOS data requires simultaneous measurement of particle velocity and shock velocity, as carried out in nuclear explosion shock wave experiments. The indirect-drive method using thermal X rays in laser-heated cavities has demonstrated the feasibility of simultaneous measurements of shock velocity and particle velocity (Hammel et al., 1993). However, very recently the absolute EOS points have also been obtained using direct irradiation (Benuzzi et al., 2002). An intermediate method known as the “impedance matching technique” (Koenig et al., 1995) involves measurement of shock velocity in two materials in stepped target configurations. The technique is used for measuring the EOS of one of the materials, using the known EOS of the other material as reference. In this article, we present the laser-induced shock velocity measurements in a thin foil single layer (Al) and layered targets (Al-Au and Al-Cu) using a 2-J/200-ps laser pulse. We use a high-speed S-20 photo cathode streak camera for shock luminosity detection. The equations of state of Al, Au, and Cu obtained using impedance matching techniques are in agreement with the reported results of SESAME. In Section 1, we report the development of a 2-J/200-ps laser chain of high contrast ratio (>5000:1) that involves a modified commercial laser oscillator. In Section 2, we present the experimental results of equation-of-state measurements of Al, Au, and Cu using impedance matching techniques. Section 3 has the error analysis and Section 4 has the results and discussion on shock velocity measurements.
The commercial laser used is a cavity-dumped active–passive mode-locked system consisting of a Nd:YAG picosecond oscillator and an amplifier as shown schematically in Figure 1. The oscillator is based on the novel resonator design utilizing intracavity spatial filtering and large mode volume that gives a high-energy laser pulse output along with a smooth beam profile. This oscillator operates at a 10-Hz repetition rate to compensate for the thermal lensing in the YAG rod and produces a high energy stability of ∼5%. The cavity dumping in the oscillator is achieved by a high-speed photodiode–Pockel's cell combination where the photodiode senses the intensity buildup inside the cavity and generates a trigger pulse for the high-speed Marx circuit driving the Pockel's cell when a predetermined intensity level is reached. The selected output pulse, ejected via a polarizer (P1), is fed to the Nd:YAG amplifier to give a laser pulse of energy of 70 mJ in a 40-ps duration at 1.064 μm. The energy and pulse duration are increased to 180 mJ and 200 ps, respectively, by using a suitable intracavity etalon. This laser system can be operated in an internal as well as an external mode. The schematic diagram of the 2-J/200-ps laser chain that consists of a modified commercial laser oscillator to be operated in a single shot, external pulse selector (EPS), two silicate Nd:Glass amplifiers (φ = 20 mm) and Faraday isolator is shown in Figure 2. In this chain, the oscillator is operated at 10 Hz to maintain the energy stability whereas the EPS, amplifiers, and Faraday isolator are operated in the single-shot mode. A centralized control unit controls the charge and fire sequence of various stages. The heart of the unit is an Intel 8085-based microcomputer that has serial I/O ports for interfacing data entry terminal and switches like Charge (Chg), Trigger (Trg), and Dump (Navathe et al., 1996). This microcomputer controls different power supplies at various stages in the laser chain through independent control modules. The external operation of the picosecond laser at 10 Hz is achieved by sending +5 V TTL from the trigger generator in the control unit to the oscillator power supply. When an amplified laser pulse in single shot mode is required, the “Chg” command from the control unit is given that initiate charging of the capacitor banks of the amplifiers and Faraday isolator. Once the voltage reaches a set level, “Trg” is initiated that enables the trigger generator designed for pulsed biasing of the cavity dumping photodiode (HP 5082-4207) in the commercial oscillator (Fig. 2) and discharges the capacitor banks of amplifiers and the Faraday isolator. The trigger generator generates a pulse in monoshot mode with an amplitude of ∼140 V and a duration of ∼80 ms that biases the diode to select one pulse from the train of laser pulses at 10 Hz. This electronic selection of the laser pulse offers reliability as compared to a mechanical shutter based on stepper motor or coil control, which is susceptible to electromagnetic noise.

Schematic of picosecond Nd:YAG commercial oscillator.

Schematic of 2-J/200-ps laser chain.
The selected single pulse output from the oscillator consists of some mode-locked train of prepulses (separated by a round trip time of ∼8 ns) followed by the main laser pulse with a contrast ratio of ∼50:1. This is due to the finite extinction of the polarizer used inside the oscillator. Such a pulse is detrimental to conducting experiments that involve laser ablation of material in thin foils as the prepulses would puncture the foil before the main pulse arrives. An EPS consisting of a single Pockel's cell between two crossed polarizers is designed and incorporated in the laser chain to increase the contrast ratio to >5000:1. The Pockel's cell is driven by two step pulses of +3.5 kV and −3.5 kV switching in ∼7 ns. The high-voltage generators of the step pulses are designed in a Marx bank configuration where the high-voltage capacitors are charged in parallel and then discharged in series through the avalanche transistors 2N5551. Each transistor is carefully selected for the same breakdown voltage (350 V) and fall time (∼2 ns) with a jitter of ±100 ps. The two high-voltage step pulses are applied to the electrodes of the Pockel's cell in a floating electrode push–pull configuration to obtain Vλ/2 operation. This configuration is specially used for cavity-dumped, mode-locked oscillators (Koechner, 1992). The trigger pulse for the Marx circuits is derived from the cavity-dumping photodiode of the oscillator by putting an additional pulse forming circuit in parallel with the existing one. This helps in getting a trigger signal well ahead of the main pulse (40 ns) and in synchronization of the laser pulse with the selector. The synchronization is achieved by putting extra passive delay using coaxial cable in the trigger signal to the Marx circuit of the cavity-dumping Pockel's cell and variable passive delay in the trigger signal to the external pulse selector drivers. The energy of the selected main pulse after the EPS is ∼100 mJ. This pulse is fed to two silicate Nd:Glass amplifiers of gain ∼4.5 to achieve laser energy of ∼2 J in 200 ps.
An intense laser beam when focussed on a thin solid target kept in vacuum with initial density ρ0 (solid density) creates hot ablating plasma at the surface of the target. Laser energy is absorbed up to the critical density surface where the plasma frequency is equal to the laser frequency. Plasma ablation in the early phase of laser pulse duration launches a compression wave in the target material due to momentum recoil. The successive compression waves generated by the laser pulse after the first compression in the initial phase travel inside the compressed material at a higher velocity than the first and develop a steady shock wave at approximately the peak of the laser pulse. However, the laser pulse required for shock generation should be free from prepulses. The shock wave propagates in the target with a shock velocity us and imparts a particle velocity up to the material behind the shock front. After the laser pulse is over, the ablation pressure and velocity begin to drop rapidly. At this time, a rarefaction wave sets in and propagates from the ablation front into the shock-compressed target. The ablation-driven shock wave propagates in the target material and heats the compressed material, thereby generating a visible optical emission when the shock unloads at the rear surface of the target.
The experimental setup to detect laser-induced shock in metals is shown in Figure 2. A good spatial beam quality (TEM00) and high-contrast laser pulse of an energy of 2 J and a duration of 200 ps from the developed laser chain is used as a driver. There were no measurable hot spots in the laser beam (measured with a beam profiler), which is due to an intracavity spatial filter and apodizer used inside the oscillator, giving TEM00 output, and also due to the fact that only two amplifiers were used in the laser chain. The optical surfaces in the laser chain were kept meticulously clean to avoid any diffraction-caused spatial intensity variations in the laser beam intensity profile. The intense picosecond laser pulse is focused to a spot diameter of ∼100 μm by an aspheric lens (focal length ∼400 mm and diameter ∼50 mm) on a planar foil target kept inside a vacuum chamber (pressure ∼10−3 mbar). The high intensity (∼1014 W/cm2) created on the front surface of the foil produces ablation of material and launches a shock wave in the medium, generating thermal radiation on unloading at the rear surface. The hot emitting rear surface behaves like a black body and its luminescence emissivity signal is collected and focused by a lens on the entrance slit (width ∼100 μm, length ∼6 mm) of a high-speed visible (S-20) streak camera (Rai et al., 1995). A CCD camera captures the streak image, which is acquired on a personal computer (PC) through a frame grabber card for final image processing. The streak camera that is used for detection of the shock breakout signal has temporal and spatial resolutions of ∼5 ps and 100 μm, respectively. A fiducial signal that serves as a marker for the arrival of the laser pulse on the front surface of the foil is also recorded, along with shock-induced luminescence by the streak camera each time the laser is fired on the target foil. This has been achieved by picking up 4% laser reflections from a glass plate (wedge angle ∼0.5°), placed before the focusing lens, and converting it to visible radiation by a second harmonic crystal 20 mm long and then sending it along an optical fiber cable at the vertical slit input of the streak camera. In the slit, the fiber tip rests below the laser focal spot where radiations from the target are expected to reach. The streak camera is triggered from a photodiode that is also used to trigger the Pockel's cell inside the laser cavity for cavity dumping. To synchronize the streak operation with the arrival of the main laser pulse, the laser pulse is optically delayed by means of a pair of fully reflective mirrors (M1 and M2) before it is focused on to a target. The arrival of the laser pulse at the streak input without any target material in the beam path is synchronized with the arrival of the fiducial signal by introducing an optical delay loop consisting of four fully reflecting mirrors (M3, M4, M5, and M6) between the focusing lens and the beam sampling glass plate (for fiducial arrangement). The synchronized fiducial and main laser pulse recorded is shown in Figure 3.

CCD image of the synchronized fiducial and main laser pulse.
Planar Al foil targets of different thicknesses were made from a standard aluminum foil (density ∼2.7 gm/cm3) of 12 μm thickness by a controlled chemical etching process. Purified NaOH pellets (assay content ∼97%) were dissolved in water and the solution was used to etch the foil. Each foil was first carefully fixed on a Plexiglass frame in such a manner as to make the surface of the foil free. The assembly was then immersed in the etching bath and held vertically during the operation. By controlling the etching time, a foil thickness down to 3.2 μm was achieved. The foil thickness was measured by weighing the foil sample of a definite dimension (2.5 × 2.5 cm2) on a microbalance. Target dimensions were chosen such that they satisfy the following criteria:
a. The laser focal spot diameter was small enough to produce the required high intensity, yet it was much larger than the target thickness to minimize two-dimensional (2D) effects, and hence, to ensure a planar shock (Trainor et al., 1979).
b. The width of the target was much larger than the diameter of the laser focal spot to avoid weakening of the shock strength by an edge rarefaction wave. This is also required to avoid the ablation plasma flow around the foil edges, which otherwise disturbs the luminosity record.
c. After termination of the driving laser pulse, a rarefaction wave propagates at a speed higher than the shock wave and eventually overtakes and attenuates it. Therefore, to ensure steady shock propagation (i.e., to avoid shock decay), the target thickness was chosen such that it satisfies the condition: d ≤ 2usτ, where d is target thickness, us is the shock velocity in the material, and τ is the laser pulse length. Typical shock velocity in Al is ∼106 cm/s and τ = 200 ps (FWHM of pulse) (Gu et al., 1996).
d. The thickness of the target was kept larger than the range of suprathermal electrons and hard X rays to avoid preheat reaching ahead of the shock wave on the rear side of the target.
We have used planar Al foils (typically 3 to 4 mm wide) of thickness 3.2 μm, 4.6 μm, 5 μm, 6 μm, 7 μm, and 8 μm. The shock breakout times for different targets were recorded at the same absorbed laser intensity. This was ensured by selecting only those data points from the large number of shock transit time data taken for each thickness of the foil used where the intensity was very nearly the same. The absorbed laser intensity data was estimated in a separate experiment by measuring the spatially integrated reflection over the entire front half space of the target surface at various incident laser intensities using an Ulbricht integrating sphere (H.C. Pant, unpubl.). A typical experimental observation of shock emergence seen as strong luminosity as recorded by the streak camera is shown in Figure 4. The shock transit times (t) were calculated with respect to the peak of the fiducial signal using the image-processing software PROMISE (Vora et al., 1996) and it was found to be linear up to a foil thickness (d) of ∼7 μm. The average shock velocity is found to be ∼2.09 × 106 cm/s for an absorbed laser intensity of ∼5 × 1013 W/cm2 as shown in Figure 5 by taking the inverse of the slope of the best linear fit to the data in t–d plane. Using a similar method, the shock velocity of ∼1.78 × 106 cm/s is found at an absorbed laser intensity of ∼3 × 1013 W/cm2.

Streak record of the fiducial and shock luminosity signals in 5-μm Al target.

Shock transit time versus thickness of Al foil for shock velocity calculation.
The particle velocities corresponding to the experimentally measured shock velocities were calculated from the us and up relationship (Marsh, 1980) using
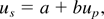
where us and up are shock and particle velocities in units of 106 cm/s. The shock pressures were calculated from the standard Rankine–Hugoniot relationship:
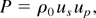
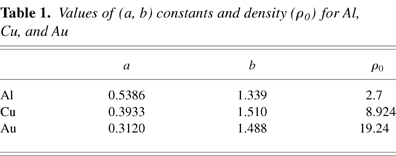
where ρ0 (gm/cm3) is the solid density. The values of a, b, and ρ0 for Al, Cu, and Au used are given in Table 1.
Values of (a, b) constants and density (ρ0) for Al, Cu, and Au
One dimensional radiation hydro code MULTI simulations (Ramis et al., 1988; Pant et al., 2002) revealed that steady shock wave propagation through Al foil requires a minimum thickness of ∼3.4 μm to achieve stability as shown in the Figure 6, which represents the simulated pressure profile (using MULTI) at different times when the laser pulse first strikes the target surface and at different distances from the front surface. Because the series of shock waves launched in the material during the initial rising portion of the laser pulse is in the accelerating phase and attains steadiness only after the peak of the laser pulse (200 ps from the base of the laser pulse as shown in Fig. 6), the fact that the shock transit time is measured from the peak of the laser pulse is obvious. This also shows that a steady shock reaches the target rear surface. The thickness of the foil target should be taken such that the shock wave is able to traverse it before the laser pulse is over. A 5-μm Al foil procured from a standard manufacturer (thickness variation ∼±0.1 μm) is thus used as a reference material to find the EOS of Au and Cu using the impedance matching technique. Au layers of ∼1.75 μm and ∼1.5 μm thick were deposited on the rear surface of Al foil employing chemical and vacuum deposition techniques, respectively. A pressure of 10−5 bar was maintained in the vacuum deposition system. Similarly ∼1-μm copper was deposited on the Al foil using vacuum deposition techniques. Suitable changes were made in the process to obtain good adhesion and to keep variation in the deposited thickness within ±0.05 μm.

Simulated pressure profiles showing steady shock propagation using MULTI 1-D hydrocode.
The shock transit time was determined for two-layer targets of 5 μm Al + 1.75 μm Au and 5 μm Al + 1.50 μm Au at the same absorbed laser intensities of 5 × 1013 W/cm2 and 3 × 1013 W/cm2, respectively, used for reference material Al. Here also, only those data points were selected, from the large number of shots taken for determining the shock transit time in layered targets, where the laser intensity was very nearly equal. As the shock transit time for the reference material Al was known, the shock transit time for the Au layers was calculated. The measured shock velocity in pure Al and layered Al + Au targets along with the calculated particle velocity and shock pressure using Eq. (1) and Eq. (2) are shown in Table 2. Typical streak records of the pure Al target along with the layered Al + Au target are shown in Figure 7a and Figure 7b, respectively. The shock luminosity signals recorded in the two targets clearly show the relative shock transit time delay. The shock transit time was also determined in a similar way for a 5-μm Al + 1-μm Cu layered target for absorbed laser intensities of 4.4 × 1013 W/cm2 and 3.9 × 1013 W/cm2. The measured shock velocity in pure Al and layered Al + Cu targets along with the calculated particle velocity and shock pressure are shown in Table 3.
EOS data for Al-Au target

EOS data for Al-Cu target


a: Streak record of the shock luminosity signal in Al target. b: Streak record of the shock luminosity signal in Al-Au layered target.
In the experiment, the target consists of Al foil as the reference material and Au (or Cu) as a test material deposited on the rear surface. Because the density of Au is higher compared to that of Al, its Hugoniot curve, defined as the locus of all the possible states in which a material can exist after shock wave compression, is located above that of Al. When a shock arrives at the interface between the two materials, a shock wave is partly transmitted through Au and partly reflected in Al. We deduce the shock velocities us using the time difference in the shock luminosity signal recorded by the streak camera. As shown in Figure 8, red and magenta lines are the Rayleigh lines (with slope values equal to the shock impedance ρ0us) that represent the final state of adiabatically compressed material (Al) attained with respect to an initial state on a pressure Hugoniot curve (black). The two slope values ρ0us for Al in the P–up plane intersect the Hugoniot curve at the points (1.16,6.58)1 and (0.93,4.46)2 at an absorbed laser intensity of ∼5 × 1013 W/cm2 and ∼3 × 1013 W/cm2, respectively. The reflected Hugoniot for Al at the two absorbed laser intensities (light and dark blue dotted curves) could be represented as H1 (2up(Al) − up), where H1 (up) is the shock Hugoniot for Al and up(Al) is the particle velocity induced by a shock wave in Al. The intersection of the Rayleigh lines for Au (green and gray) with the reflected Hugoniot curves for Al gives the EOS point of Au on the pressure Hugoniot curve (orange). The final state determined this way, as shown in Figure 8, gives pressure and the particle velocity in Au as 13.47 Mbar and 0.59 × 106 cm/s and 9.01 Mbar and 0.47 × 106 cm/s at absorbed laser intensities of 5 × 1013 W/cm2 and 3 × 1013 W/cm2, respectively. Figure 9 shows the final state of Cu with respect to the initial state on a pressure Hugoniot curve that also lies above that of Al. The pressure and particle velocity in Cu is found to be 10.38 Mbar and 0.76 × 106 cm/s and 8.90 Mbar and 0.70 × 106 cm/s at absorbed laser intensities of 4.4 × 1013 W/cm2 and 3.9 × 1013 W/cm2, respectively.

Graph representing final state of Au on pressure Hugoniot using an impedance matching technique.

Graph representing the final state of Cu on pressure Hugoniot using an impedance matching technique.
The laser-induced shock generation in thin metal targets for EOS studies aims at minimizing the possible errors that are introduced in the shock velocity, particle velocity, and pressure. The impedance matching technique analysis involves: (1) Evaluation of theEOS (P, ρ, E, us, up) point in the reference material from the measured shock velocity, (2) construction of reflected pressure Hugoniot curve at the reference point of the shock reflected in the unknown material, (3) intersection of the reflected Hugoniot with the Rayleigh line of unknown material that gives the common EOS point in the P–up plan. Thus at the intersection point of the reflected Hugoniot and the Rayleigh lines the error in pressure is quadrature and is given by
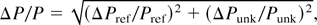
where ΔPref/Pref is the error in the reference material (Al) and ΔPunk/Punk is the error in the unknown material used (Cu). Because P = ρ0usupαρ0us2 on a pressure Hugoniot curve and Pαρ0us on a Rayleigh line, Eq. (3) leads to
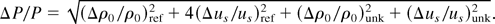
Ignoring the density errors in reference and unknown material (Rothman et al., 2002), Eq. (4) leads to
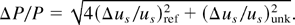
The fractional errors are assumed to be independent but they are equal for each step. The possible errors that contribute to the shock velocity are errors due to the foil thickness variation, transit time, and streak camera calibration. Thus, from Eq. (5), the variation in shock velocity can be written as
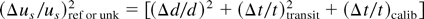
where Δd/d is the thickness variation error, (Δt/t)transit is the transit time error, and (Δt/t)calib is the error in streak camera calibration.
The variation in the coating thickness for vacuum deposition is given by
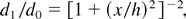
where d0 is the deposited thickness at the center and d1 is deposited thickness at the target boundary with dimensions of 25.4 mm × 25.4 mm. In the coating unit x = 12.7 mm from the center of the target whereas the height of the target from the source was h = 100 mm. Thus the deposited thickness by vacuum deposition has a variation of ∼±0.05 μm for Au as well as Cu. The thickness variation of the Au deposited by the chemical process is also assumed to be the same as vacuum deposition because the deposition area is very small. The streak camera used in our experiment has a temporal resolution of ∼5 ps for the streak rate of 15.62 mm/ns. Therefore, for a streak camera calibration error (Δt/t)calib ∼ 0.3% and a transit time CCD pixel value of ∼3.2 ps, the error in pressure for Al (reference) is calculated to be ∼ ± 5% from the relation
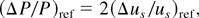
whereas the errors in pressure for Au and Cu as per Eq. (5) are ∼±7% and ±9%, respectively. The calculated errors in shock velocity, particle velocity, and pressure for Al, Au, and Cu are shown in Table 2 and Table 3.
We have compared the experimental data for shock velocity in Al, Au, and Cu with the SESAME data (Bennet et al., 1978; Batani et al., 1996; Benuzzi et al., 1996a, 1996b; Evans et al., 1996a, 1996b; Jones et al., 1966; Altshuler et al., 1962; Mitchell et al., 1991; Trunin et al., 1969; Kormer et al., 1962). Figures 10 and 11 show the experimental data points plotted on the SESAME curve of Au and Cu, respectively, along with the results of other laboratories. The experimentally obtained a and b constants as per Eq. (1) are in close agreement with the LASL data (Marsh, 1980). The published data gives (a, b) = (0.312,1.51) for Au and (0.3933,1.51) for Cu, which compares well with the experimental values of (a, b)Au = (0.312,1.495) and (a, b)Cu = (0.3933,1.509). The experimental pressure multiplication factor (m = PAu or Cu/PAl) of 2.01 (for Au) and 1.66 (for Cu) at the interface of the layered targets is in close agreement with the theoretical formulations. The simulation result for the two layered targets also predicts similar results of pressure enhancement (Pant et al., 2002). Our shock velocity measurements and Hugoniot EOS points are in fairly good agreement within the shock transit time error of ±3% and ±7% for reference and unknown materials, respectively. Thus, our shock pressure values determined are correct within an error of ±5% for reference material and ±7% to ±9% for the unknown material as per the error analysis. The low values of errors obtained in the present experiment are due to the use of a high-resolution streak camera that resulted in low transit time error. Further, the optimized streak velocity ∼15.62 mm/ns used in the experiment has resulted in a low CCD pixel value error and has helped in reducing the possible errors, which is not possible otherwise in experiments that use step targets (Koenig et al., 1995). The small area of the reference material used for deposition of the test materials has also helped in reducing the errors as per Eq. (7). However, the overall errors in pressure can be minimized within ±3% to ±5% by using random phase plates or phase zone plates (Gu et al., 1996) in a direct-drive approach where the uniform laser illumination generates a planar shock or indirect drive approach (Rothman et al., 2002). In the present experiment, no attempt was made to achieve a flat shock profile. However, special care was taken in removing prepulses present in the laser beam. The sharp rising shock luminosity signal shows that the preheating effects are negligible in our case (Benuzzi et al., 1998). This fact was also corroborated from the simulated temperature profiles using the MULTI 1-D code as shown in Figure 12. According to the simulation results, the temperature of the rear surface of the target remains at only 0.2 eV, which is nearly insignificant relative to the shock luminosity signal appearing from the rear side due to the ∼5 eV temperature. The optimum foil thickness of 5 μm for Al has also helped in minimizing the preheat effects due to hard X rays (Honrubia et al., 1998). This has been explained on the basis of various opacity models suggesting that for a thin foil target (Al at 5.0 μm or so), the suprathermal X-ray component (0.8–1.5 keV) will not have ample time to heat the rear surface of the foil and the shock signal will pass long before the arrival of such X-ray photons. Typically, such hard X-ray components takes about 1–2 ns to diffuse to the rear surface. Further, the laser intensities are well within the limits where hot electrons generation may not lead to the preheat effect.

EOS Hugoniot data points (Au) of present experiment and other laboratories on SESAME curve.

EOS Hugoniot data points (Cu) of present experiment and other laboratories on SESAME curve.

Simulated temperature profiles representing negligible preheat using MULTI 1-D hydrocode.
The commercial mode-locked laser has been modified for single shot operation to produce a laser pulse of high contrast. The external pulse slicer designed helps in increasing the contrast ratio to >5000:1. We have shown the feasibility of using a simple laser driver system (Nd:YAG, 2 J, 1.06 μm, 200 ps) for conducting shock-wave experiments for EOS measurements of gold and copper in a thin layered target at moderate pressures in the 8–13 Mbar range. A fast streak camera system coupled with a fiber-based fiducial signal marker records the shock breakout times. The results are quite consistent with theoretical as well as experimental data published by other laboratories. An impedance matching technique was successfully used to find the pressure in gold and copper in multilayered Al + Au and Al + Cu targets within errors of ±10%. The laser-driven shock velocities and particle velocities obtained for gold and copper are in excellent agreement with the reported results of other laboratories including SESAME data. The pressure amplification factors of 2 and 1.66 have been derived in Al + Au and Al + Cu layered targets, respectively, as per the theoretical calculations and MULTI simulations.
We are extremely grateful to Dr. D.D. Bhawalkar for his constant support and guidance in the present work. We are also indebted to Dr. S.K. Sikka for fruitful discussions and many helpful suggestions. Dr. S.N. Vyas and Mr. R.K. Khare and his colleagues are acknowledged for their help in target fabrication and characterization. Members of high power glass laser and electronics group deserve our special thanks for their technical help and support during the experiment.

Schematic of picosecond Nd:YAG commercial oscillator.

Schematic of 2-J/200-ps laser chain.

CCD image of the synchronized fiducial and main laser pulse.

Streak record of the fiducial and shock luminosity signals in 5-μm Al target.

Shock transit time versus thickness of Al foil for shock velocity calculation.
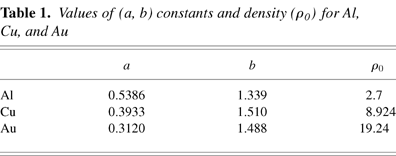
Values of (a, b) constants and density (ρ0) for Al, Cu, and Au

Simulated pressure profiles showing steady shock propagation using MULTI 1-D hydrocode.

EOS data for Al-Au target

EOS data for Al-Cu target

a: Streak record of the shock luminosity signal in Al target. b: Streak record of the shock luminosity signal in Al-Au layered target.

Graph representing final state of Au on pressure Hugoniot using an impedance matching technique.

Graph representing the final state of Cu on pressure Hugoniot using an impedance matching technique.

EOS Hugoniot data points (Au) of present experiment and other laboratories on SESAME curve.

EOS Hugoniot data points (Cu) of present experiment and other laboratories on SESAME curve.

Simulated temperature profiles representing negligible preheat using MULTI 1-D hydrocode.