Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T09:23:16.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Enhanced Raman scattering of a rippled laser beam in a magnetized collisional plasma

Published online by Cambridge University Press:  01 March 2004

NARESHPAL SINGH SAINI  and
TARSEM SINGH GILL
NARESHPAL SINGH SAINI
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
TARSEM SINGH GILL
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
Rights & Permissions [Opens in a new window]

Abstract

In the laser–plasma interaction experiments, self-focusing and filamentation affect quite a large number of other parametric processes including stimulated scattering processes. Nonlinearity considered in the present problem is the collisional type. The coupling between the main beam, ripple, and excited electron plasma wave is strong. Authors have investigated the growing interaction of a rippled laser beam with an electron plasma wave leading to enhanced Raman scattering. An expression for scattered power is derived and the effect of the externally applied magnetic field on the enhancement of scattered power is observed. From computational results, it is observed that the effect of increased intensity of the main beam leads to suppression of power associated with the Raman scattered wave.

Keywords

Collisional plasmaCouplingRaman scatteringRippled laser beam
Type
International Conference on the Frontiers of Plasma Physics and Technology
Information
Laser and Particle Beams , Volume 22 , Issue 1 , March 2004 , pp. 35 - 40
Copyright
2004 Cambridge University Press

1. INTRODUCTION

The stimulated scattering processes and filamentation of laser light remain key issues of laser–plasma interactions relevant to inertial confinement fusion (ICF). In the stimulated Raman scattering (SRS), incident light on plasma is converted into an electron plasma wave and low-frequency scattered photons. Two major problems associated with SRS are as follows:

  1. First, the scattered wave represents a substantial amount of wasted energy as SRS yields are as high 25%.
  2. Second, the large amplitude plasma wave produces superthermal electrons that penetrate and preheat the target core, thereby preventing the efficient implosion.

Furthermore, self-focusing and filamentation are other basic issues to be resolved for the success of ICF. In the laser–plasma experiments, the filamentary structure created in underdense plasma undergoes self-focusing by the same mechanism as that of the main beam. The origin of filamentation instability may be attributed to a small-scale intensity spike associated with the main beam. Particularly in the hot spots of the laser beam, self-focusing or filamentation grows unstably through a feedback mechanism of increased electron thermal pressure via ponderomotive force or other nonlinear mechanisms. The resulting redistribution of the carriers leads to an increased index of refraction which further results in concentration of intensity in the regions of hot spots. Thus, perturbation grows at the cost of the main beam and the overall effect is distortion of propagation characteristics, inefficient laser–energy coupling to the target, and a loss of symmetry of the energy deposition, leading to hydrodynamical instabilities of the target.

In theoretical studies, many interesting properties of stimulated back scattering, self-focusing, and filamentation have been carried out separately, ignoring interplay among them. There is also no reason to separate the evolution of these instabilities in the nonlinear regime where they coexist and affect each other (Amin et al., 1993). It is important to investigate and understand interplay among various instabilities. Liu and Tripathi (1995) have recently studied the thermal effects on coupled self-focusing and Raman scattering of laser beams in a self-focused plasma channel. In light of considerable current interest in self-focusing and SRS (Short & Simon, 1998; Russell et al., 1999; Fuchs et al., 2000) and in view of earlier work (Sodha et al., 1981; Singh and Salimullah, 1987; Saini & Gill, 2002), we here study the growing interaction of a rippled laser beam with a electron plasma wave mode leading to enhanced Raman scattering for magnetized collisional plasma. This model was used earlier in other nonlinear excitation processes (Singh & Singh, 1990, 1999; Saini & Gill, 2002). This model takes care of whole beam self-focusing, small-scale self-focusing, and their combined effect on the excitation of a plasma wave that consequently affects the stimulated scattering processes. Thus, it is important to investigate nonlinear coupling of self-focusing, filamentation, and SRS. In the case of magnetized collisional plasma the nonlinearity arises due nonuniform heating of the carriers along the wave front, and the redistribution of carriers is affected by the change in the static magnetic field.

2. SOLUTION OF THE WAVE EQUATION

Consider the propagation of a laser beam of angular frequency ω0 in a homogeneous magnetized plasma along the externally applied static magnetic field B0 coincident with the z-axis. The initial intensity distributions of the main beam and the ripple are given by

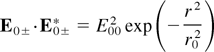
and

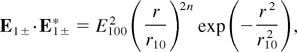
respectively. Here n is a positive number, r2 = x2 + y2, and r10 is the width of the ripple. As n increases, the maximum (rmax = r10n1/2) of the ripple shifts away from the axis. The ripple is symmetrically superimposed on the main Gaussian beam. In collisional magnetoplasma, when ν2 << (ω0 − ωc)2, we obtain a modified carrier density that is given by (Sodha et al., 1983)

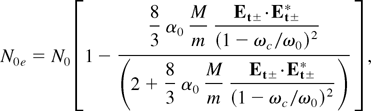
where α0 = e2/(16kBT0mω02),Et± = E0± + E1± and ε± = ε0± + Φ±(Et± +·Et±*). In WKB approximation, we can write the wave equation for the total electric vector, which leads to the following equations (for one mode) for the main beam and the ripple:

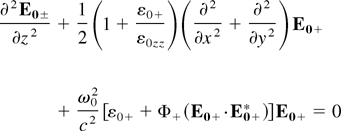
and

For the sake of simplicity, we shall drop the subscript + from subsequent analysis. Following Akhmanov et al. (1968) and Sodha et al. (1976), the solutions of Eqs. (4) and (5) are obtained and the dimensionless beam width parameters of main beam f0 and ripple f1 are governed by the following equations:

where

with

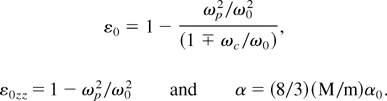
The initial conditions on f0 and f1 for a plane wave front, are df0 /dz = 0 = df1 /dz and f0 = 1 = f1 at z = 0. The expression for the growth rate of the ripple can be written as

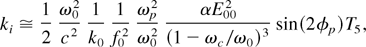
with

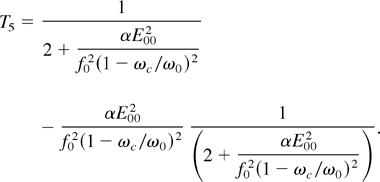
3. EXCITATION OF ELECTRON PLASMA WAVE (EPW)

A weak electron plasma wave is nonlinearly coupled to a rippled laser beam via modified background density. Thus, self-focusing of the main beam, ripple, and the dynamics of growth of the ripple, all substantially affect the excitation of the plasma wave. Using perturbation analysis and Sodha et al. (1981), it is possible to show the excitation of EPW by the following equation:

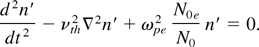
Using WKB and paraxial ray (PR) approximations and following the approach developed by Akhmanov et al. (1968) and Sodha et al. (1976), the dimensionless beam width parameter fp of the plasma wave is governed by the following equation:

4. ENHANCED RAMAN SCATTERING

Interaction of the incident pump (ω0, k0) with the electron plasma wave (ω, k) leads to generation of a scattered wave (ωS, kS). Using the approach in Singh and Salimullah (1987), the wave equation for the scattered electric field can be derived as

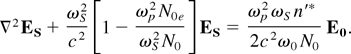
We assume the following solution for Es:

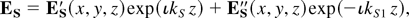
where

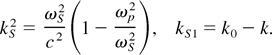
Equation (13) can be solved following the procedure of Akhmanov et al. (1968), Sodha et al. (1976), and Singh and Salimullah (1987). The dimensionless beam width parameter fs of the scattered beam is governed by the following equation:

Finally, the total scattered power of the scattered laser beam is given by (Singh, 1981)

where Q1 = kSSS + k0S0 − kSP + (kS + kS1)z and

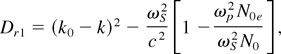
with Dr1 = Dr1(0) at z = zc and r = 0.

5. DISCUSSION

It is obvious from the present analysis that because of the coupling between the main beam and ripple, the ripple can grow/decay inside the plasma and the growth rate (ki) is given by (9). As is apparent from this expression, it depends on pump and plasma parameters. Besides that, it depends on the angle between the ripple and main beam and the externally applied magnetic field. We have chosen the following set of parameters for numerical calculations:

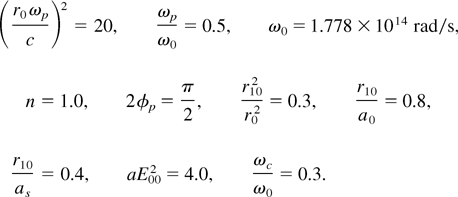
Equation (6) is a second-order, nonlinear, ordinary differential equation, governing the focusing/defocusing of the main beam as it propagates through the plasma. If the first term is large in comparison to the second, then diffraction dominates over the nonlinear phenomenon, leading to defocusing of the beam. The situation is quite the opposite when the second term is larger than the first and self-focusing of the beam is observed. It must be mentioned that relative magnitudes of these terms keep on changing with the distance of propagation. We have solved all equations numerically using the Runge–Kutta method.

Equation (7) governs the dynamics of the ripple intensity with the distance of propagation. As is apparent from the form of (7), its structure is similar to (6) for f0 and it is also a nonlinear, ordinary differential equation. Besides that, the beam width parameter f0 of the main beam appears in this equation for f1. Apparently, the focusing of the main beam drastically affects the focusing of the ripple.

In Figure 1, we have plotted beam width parameter f1 as a function of the normalized distance of propagation ξ(=zc/ω0r102) for two values of n, with αE002 = 4.0, ωc /ω0 = 0.6, and the other chosen parameters are the same. Curve 1 is for n = 1, whereas Curve 2 is for n = 2. The smaller the value of n, the larger oscillatory self-defocusing/focusing is observed.

Beam width parameter f1 of the ripple plotted against the normalized distance of propagation ξ(= zc/ω0r102) in a collisional magnetoplasma for the chosen set of parameters. Curve 1 is for n = 1.0 and Curve 2 for n = 2.0.

Figure 2 depicts the variation of the beam width parameter fp of the excited plasma wave for the above mentioned set of parameters and for three values of the magnetic field. Curve 1 is for ωc /ω0 = 0.0, Curve 2 is for ωc /ω0 = 0.3, and Curve 3 is for ωc /ω0 = 0.6. It is observed that an increase in the magnetic field not only slows down the self-focusing, but also leads to oscillatory defocusing/focusing of the beam. This is due to reduced nonlinear coupling of the electron plasma wave to the rippled laser beam with an increasing magnetic field.

Beam width parameter fp of the excited plasma wave plotted against the normalized distance of propagation ξ for different values of the magnetic field; the other parameters are the same. Curve 1 is for ωc /ω0 = 0, Curve 2 corresponds to ωc /ω0 = 0.3, and Curve 3 corresponds to ωc /ω0 = 0.6.

The excited electron plasma wave is so strong that it nonlinearly interacts with the main beam, leading to a Raman-scattered wave. Equation (15) determines the dynamics of self-focusing of the scattered wave as a function of ξ. We observe here that f0, f1, and fp jointly determine the focusing/defocusing of the scattered wave and consequently the variation of the normalized scattered power P (= PS /P0) as a function of ξ. In Figure 3, Curve 1 is for ωc /ω0 = 0.0, Curve 2 is for ωc /ω0 = 0.3, and Curve 3 is for ωc /ω0 = 0.6. For lower values of the magnetic field, however, scattered power depends on focusing of f0, f1, and fp as well as fs, but is peaked dominantly by f1. However, a low magnetic field suppresses the scattered power. But when the magnetic field is increased to ωc /ω0 = 0.6, normalized scattered power P reaches as high as 8% with the distance of propagation. Moreover, scattered power P is dominantly determined by focusing of the main beam and plasma wave as well as the scattered wave. Besides other parameters, the ripple dynamics and magnetic field play a significant role for scattered power.

Variation of the normalized power P(= PS /P0) with the normalized distance of propagation ξ for different values of the magnetic field; the other parameters are the same. Curve 1 is for ωc /ω0 = 0, Curve 2 corresponds to ωc /ω0 = 0.3, and Curve 3 corresponds to ωc /ω0 = 0.6.

Figure 4 displays the normalized scattered power as a function of ξ for three different values of intensity parameter and a fixed value of the magnetic field (ωc /ω0 = 0.6). Curve 1 is for αE002 = 4.0, Curve 2 is αE002 = 5.0, and Curve 3 is for αE002 = 6.0. The following observations are made:

  1. Scattered power is highest for the low intensity parameter.
  2. An increase in intensity suppresses the scattered power.
  3. There is a shift in the maximum scattered power with ξ for different values of the intensity parameter. It is due to phase mixing of various terms in the expression for scattered power as these terms keep on varying with ξ.

Variation of the normalized power P(= PS /P0) with the normalized distance of propagation ξ for different values of intensity with ωc /ω0 = 0.6; the other parameters are the same. Curve 1 is for αE002 = 4.0, Curve 2 is αE002 = 5.0, and Curve 3 is for αE002 = 6.0.

6. CONCLUSIONS

The introduction of a magnetic field weakens the nonlinear term, leading to decreased self-focusing of the ripple. This behavior becomes more succinct as is obvious from Figure 1 and Figure 2. Further, the effect of an increasing magnetic field leads to a decrease in coupling of EPW to the rippled laser beam. This behavior is quite opposite to the one observed earlier (Saini & Gill, 2002). We also obtain high scattered power for low intensity and wiggles in the scattered power are smoothed. This behavior is also contrary to the one observed earlier (Saini & Gill, 2002). Thus, the magnetic field plays a crucial role in the dynamics of the rippled laser beam propagation in plasma.

References

REFERENCES

Akhmanov, S.A., Sukhorbikov, A.P. & Khokhlov, R.V. (1968). Sov. Phys. Usp. 10, 609.CrossRef
Amin, M.R., Capjack, C.E., Frycz, P., Rozmus, W. & Tikhonchuk, V.T. (1993). Two-dimensional studies of stimulated Brillouin scattering, filamentation, and self-focusing instabilities of laser light in plasmas. Phys. Fluids 5, 3748–3764.CrossRefGoogle Scholar
Fuchs, J., Labaune, C., Depierreux, S., Tikhonchuk, V.T. & Baldis, H.A. (2000). Stimulated Brillouin and Raman scattering from a randomized laser beam in large inhomogeneous collisional plasmas. I. Experiment Phys. Plasmas 7, 4659–4668.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (1995). Thermal effects on coupled self-focusing and Raman scattering of a laser in a self-consistent plasma channel. Phys. Plasmas 2, 3111–3114.CrossRefGoogle Scholar
Russell, D.A., DuBois, D.F. & Rose, H.A. (1999). Nonlinear saturation of stimulated Raman scattering in laser hot spots. Phys. Plasmas 6, 1294–1317.CrossRefGoogle Scholar
Saini, N.S. & Gill, T.S. (2002). Advances in contemporary physics & energy (supplement)New Delhi, India: Allied Publishers Pvt. Ltd., 111–127.
Short, R. W. & Simon, A. (1998). Collisionless damping of localized plasma waves in laser-produced plasmas and application to stimulated Raman scattering in filaments. Phys. Plasmas 5, 4134–4143.CrossRefGoogle Scholar
Singh, A. & Singh, T. (1990). The effect of a static magnetic field on the growth of a rippled electromagnetic beam. J. Plasma Phys. 43, 465–474.CrossRefGoogle Scholar
Singh, N. & Singh, T. (1999). Growth of laser ripple in a collisional magnetoplasma and its effect on plasma wave excitation. J. Plasma Fusion Res. 2, 423–426Google Scholar
Singh, T. (1981). Excitation of waves and scattering phenomena in Plasmas, PhD Thesis, Indian Institute of Technology Delhi: New Delhi, India.
Singh, T. & Salimullah, M. (1987). Nonlinear Interaction of a Gaussian EM Beam with an Electrostatic Upper Hybrid Wave: Stimulated Raman Scattering. IL Nuovo Cimento 9, 987–998.CrossRefGoogle Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Progress in Optics 13, 169.
Sodha, M.S., Singh, T., Singh, D.P. & Sharma, R.P. (1981). Growth of laser ripple in a plasma and its effect on plasma wave excitation. Phys. Fluids 24, 914–919.CrossRefGoogle Scholar
Sodha, M.S., Tewari, D.P. & Subbarao, D. (1983). Contemporary Plasma Physics. Delhi, India: Macmillan India Ltd.
Figure 0

Beam width parameter f1 of the ripple plotted against the normalized distance of propagation ξ(= zc/ω0r102) in a collisional magnetoplasma for the chosen set of parameters. Curve 1 is for n = 1.0 and Curve 2 for n = 2.0.

Figure 1

Beam width parameter fp of the excited plasma wave plotted against the normalized distance of propagation ξ for different values of the magnetic field; the other parameters are the same. Curve 1 is for ωc /ω0 = 0, Curve 2 corresponds to ωc /ω0 = 0.3, and Curve 3 corresponds to ωc /ω0 = 0.6.

Figure 2

Variation of the normalized power P(= PS /P0) with the normalized distance of propagation ξ for different values of the magnetic field; the other parameters are the same. Curve 1 is for ωc /ω0 = 0, Curve 2 corresponds to ωc /ω0 = 0.3, and Curve 3 corresponds to ωc /ω0 = 0.6.

Figure 3

Variation of the normalized power P(= PS /P0) with the normalized distance of propagation ξ for different values of intensity with ωc /ω0 = 0.6; the other parameters are the same. Curve 1 is for αE002 = 4.0, Curve 2 is αE002 = 5.0, and Curve 3 is for αE002 = 6.0.