The development of the chirped-pulse amplification (CPA) (Strickland & Mourou, 1985) has made multiterawatt compact short-pulse laser (Danson et al., 2005) readily available in laboratories. Consequently, there have emerged many new frontier research areas in both applied and fundamental physics (Umstadter, 2001, 2003; Giulietti et al., 2005; Lifschitz et al., 2006). Among these, the development of laser-driven particle acceleration mechanism (Modena et al., 1995; Esarey et al., 1996; Roth et al., 2005; Glinec et al., 2005; Yin et al., 2006) is a fast advancing area of scientific research because of its pivotal role in industries and medicine (Kitagawa et al., 2004; Sari et al., 2005; Mangles et al., 2006). The early schemes envisaged the production of a large amplitude plasma wave in different accelerators such as the plasma wakefield accelerator (Katsouleas, 1986; Suk et al., 2001), the plasma beat-wave accelerator (Rosenbluth & Liu, 1972; Shvets & Fisch, 2001), the laser wakefield accelerator (Umstadter et al., 1994; Pukhov & Meyer-ter-Vehn, 2002), the resonant laser-plasma accelerator (Kawata et al., 2005; Sakai et al., 2006; Nakamura et al., 2006; Koyama et al., 2006), and the self-modulated laser wakefield accelerator (Sprangle et al., 1992; Hafz et al., 2006).

Direct laser electron acceleration in a vacuum has received attention in recent years. The availabilities of high power lasers renewed the research interest of charged particle acceleration in a vacuum. A vacuum as a medium for electron acceleration has some advantages over plasma. The problems inherent in laser-plasma interaction such as instabilities are absent in a vacuum. Furthermore, peak energy attained by the electron increases with initial electron energy and it is easier to inject pre-accelerated electrons in a vacuum than that in plasma. Vacuum acceleration by nonlinear mechanism was invented by Hora (1988). Laser acceleration in a vacuum has been studied theoretically (Cicchitelli et al., 1990; Hauser et al., 1994; Stupakov & Zolotorev, 2001; Wang et al., 2001; He et al., 2003; Kawata et al., 2005; Liu et al., 2006) for many years and recently some schemes have been proposed for experimental verification (Malka et al., 1997). The major difficulty in using a laser beam in a vacuum to accelerate the electrons is that the phase velocity of the electric field of the accelerated electrons is larger than the speed of light. However, theoretical analysis shows that the electrons may be accelerated when the phase slip is within the range of the accelerating phase (Esarey et al., 1995; Hartemann et al., 1998; Hora et al., 2000; Gupta & Ryu, 2005). The experimental results on the MeV electron generation by the Lorentz force of an ultra-intense linearly polarized laser pulse in a vacuum were reported by Malka et al. (1997). Recently, Singh (2005) has studied the electron acceleration by using a chirped laser and concluded that a suitable frequency chirp of the laser enhances the electron energy during acceleration in a vacuum. As previously reported (Gupta & Suk, 2006a, 2006b), the most surprising and meaningful result for a vacuum electron acceleration in the presence of a magnetic field is that when a suitable frequency chirp of the laser is introduced, the electron not only accelerates to high energy, but also retains it even after passing of the laser pulse.

As we know, the electron energy gain during laser acceleration in a vacuum depends mainly on the laser intensity, because the longitudinal momentum of the electron is proportional to the square of the laser intensity amplitude. Two crossed lasers have some advantages over single laser for electron acceleration in a vacuum. If the frequencies, amplitudes, and polarizations of both lasers are chosen such that only axial field survives, then the theoretical analysis can be considered linear. Two crossed lasers having same amplitude and frequency are responsible for interference in a vacuum (Maher & Hall, 1976; Hora, 1988; Salamin & Keitel, 2000). The resultant field amplitude enhances due to the constructive interference, resulting in improvement to the electron energy gain compare to the former cases. We emphasize the previous work to propose a scheme for electron acceleration by using two chirped lasers and find some additional results. Two high-intensity chirped lasers, with the same amplitude, and frequency, crossing at an arbitrary angle in a vacuum, interfere, causing modulation of laser intensity. The resultant field accelerates the electron, injected externally at a certain angle δ to the z-direction. The frequency chirp plays an important role to enhance the electron energy during this mechanism.

We consider two chirped Gaussian laser pulses propagate in a vacuum at arbitrary crossing angles of θ and −θ with respect to the z-axis such that their focal points intersect at the origin (z = 0). The electric field of the first chirped laser (incident at an angle of θ with respect to the z-axis) consists of a transverse and longitudinal component. In the paraxial approximation, λ₀ << r₀ where λ₀ is the wavelength of the laser, the electric field components of the first laser can be written as

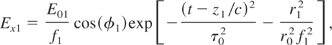
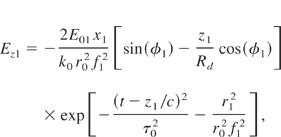
where φ₁ = k₀ z₁ − ω₀(z)t + (z₁ r₁²/R_d r₀² f₁²) − tan⁻¹(z₁ /R_d) + φ₀, f₁² = 1 + (z₁ /R_d)², ω₀(z) = ω₀₀ [1 − q(z − ct)], k₀ = ω₀(z)/c, R_d = k₀ r₀²/2 is the Rayleigh length, x₁ = x cos θ − z sin θ, y₁ = y, z₁ = x sin θ + z cos θ, r₁² = x₁² + y₁² + z₁², r₀ is the minimum laser spot size, ω₀₀ is the laser frequency at z = 0, q is the frequency chirp parameter, τ₀ is the pulse duration of the laser, φ₀ is a constant, and c is the speed of light in a vacuum. The magnetic field related to the laser pulse can be calculated by

.

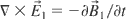
Here it is mentioned that we included the longitudinal component of the laser electric field to realize this scheme. The longitudinal field component is important near the focus of the laser beam in a vacuum as predicted earlier. Although for an idealized approach, one may neglect the longitudinal component of the laser electric field and may not adopt focusing in the transverse dimensions. But the spot-sizes of the laser beams to be infinite in that case. That is a very strong approximation. Unless this restriction is removed, no meaningful result can be obtained.

The field components for another laser (incident at an angle of −θ with respect to the z-axis) can be written from Eqs. (1) and (2), to replace the subscript 1 by 2. Both lasers have the same amplitude and frequency, and are properly phased such that the resultant transverse electric field components vanish for all points on the axis, while the axial field components survive. The magnetic field also vanishes for all points of the z-axis in this arrangement. After the constructive interference, only the non-vanishing axial (x = 0,y = 0) electric field component will be presented, that is.,

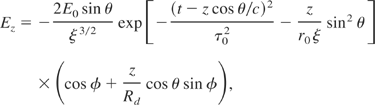
where φ = k₀ z cos θ − ω₀(z)t + z cos³ θ tan² θ/r₀ξ − tan⁻¹[(z/R_d)cos θ] + φ₀, ξ = 1 + (z/R_d)² cos² θ, and E₀ = E₀₁ = E₀₂. Here φ is an important factor, which is the function of z and t, and shows the effect of frequency chirp.

The equations governing electron momentum and energy can be written as

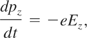
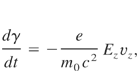
where γ = (1 + p_z²/m₀² c²)^1/2 is the relativistic factor and −e and m₀ are the electron's charge and mass, respectively. The x- and y-components of the above equations result in no motion because of the vanishing of the magnetic field on the z-axis.

We did some computer simulations to solve Eqs. (4) and (5) for axial electron velocity v_z and electron energy γ as a function of distance z for different parameters by assuming the initial electron energy to be γ₀. An electron is injected initially at a certain angle (δ) in z-direction with momentum

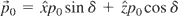
, where p₀ = m₀ v₀ is the initial momentum of the electron, and v₀ is the initial velocity of the electron. The results are presented in the form of dimensionless variables.

Throughout this paper, time and length are normalized by 1/ω₀₀ and c/ω₀₀, respectively. Momentum, energy, and velocity are normalized by m₀ c,m₀ c², and c, respectively. The laser intensity parameters are normalized as a₀ = eE₀ /m₀ω₀₀ c.

In all simulations below, we set parameters as: a₀ = 3 (corresponding to the laser intensity I₀ = 1.25 × 10¹⁹ W/cm², wavelength λ₀ = 1 μm, spot size r₀ = 15 μm, and pulse duration τ₀ = 150 fs), a₀ = 7 (corresponding to I₀ = 8.1 × 10¹⁹ W/cm², λ₀ = 0.8 μm, r₀ = 10 μm, τ₀ = 100 fs), initial electron velocities 0, 0.9c, and 0.95c, crossing angles θ = 0.1 radian and θ = 0.06 radian corresponding to the maxima for un-chirped and chirped lasers, respectively, a suitable frequency chirp is used corresponding to the maximum electron energy gain, and the electron is injected at an angle δ = 10⁰ with respect to the z-direction.

Figure 1a shows the longitudinal components of the velocity of a rest electron for the laser intensity parameter a₀ = 3 without a frequency chirp (dotted line) and with a frequency chirp (solid line). The lasers are crossed at the angles of θ = 0.1 (for un-chirped lasers) and θ = 0.06 radian (for chirped lasers). The rest electron is injected at an angle δ = 10⁰ with the z-direction. Due to the effect of a frequency chirp (for chirp parameter q = 0.1 × 10⁻²), the electron rotates around the propagation direction of the laser initially, and then travels with the velocity of light. The electron of zero initial velocity does not achieve the velocity of light for un-chirped lasers. Figure 1b shows the same, where the initial electron velocity is taken 0.9c. It is observed that if the electron has sufficient high initial velocity, then it can move with the speed of light without frequency chirp.

Normalized Electron velocities vz as a function of the normalized distance z with a frequency chirp (solid line) and without a frequency chirp (dotted line) for (a) rest electron and (b) initial electron velocity 0.9c. The normalized parameters are a0 = 3 (corresponding to the laser intensity I0 = 1.25 × 1019 W/cm2, wavelength λ0 = 1 μm), r0 = 45 (for spot size r0 = 15 μm), τ0 = 25 (for pulse duration τ0 = 150 s), α = 5 × 10−3, θ = 0.1 radian, and δ = 109.

Figure 2a shows the variation of the electron energy with distance for the initial electron energy γ₀ = 3 and the laser intensity amplitudea₀ = 3. The lasers are crossed at the crossing angles of θ = 0.1 radian and θ = 0.06 radian without frequency chirp (q = 0, dotted line), and with frequency chirp (q = 0.1 × 10⁻², solid line), respectively. It is found that the intensity maxima occurred due to the constructive interference at a crossing angle θ = 0.1 radian for un-chirped lasers and at θ = 0.06 radian for chirped lasers. The electron experiences a force by the resultant field of the lasers and gains high energy during acceleration. The electron accelerates to high energy, if a suitable frequency chirp is introduced. The increasing wavelength of the laser keeps the electron in accelerating phases, which provides extra momentum to the electron. Therefore, with a suitable frequency chirp (q = 0.1 × 10⁻²), the electron not only accelerates to high energy but also retains it up to a long distance after passing of the laser pulses. However, the electron gains energy without frequency chirp because of the high intensity of the laser, but it is less compare to the energy gain in the case of chirped lasers. Furthermore, for un-chirped lasers, the electron can not retain enough energy after passing of the laser pulses.

Electron energy γ as a function of z with a frequency chirp (solid line) and without a frequency chirp (dotted line) for the normalized laser intensity (a) a0 = 3, (b) a0 = 7, and (c) a0 = 10. Other normalized parameters are same as used in Figure 1.

Figure 2b is for higher laser intensity (a₀ = 7) corresponding to a suitable frequency chirp (q = 0.5 × 10⁻², solid line) and the other parameters are the same as used in the former case. In this case, the electron gains very high energy (∼1000m₀ c²) during acceleration. It is seen that for certain laser intensity, a suitable frequency chirp parameter are required to maximize the electron energy gain. Figure 2c is for much higher laser intensity (a₀ = 10). In this case, our equations may yield about 750 MeV of electron energy with a suitable frequency chirp (q = 1.2 × 10⁻¹). Such field intensity is available nowadays, so the predictions of our model may be realized in an experiment easily. Very high electron energy may be achieved if the electron is injected with finite kinetic energy between ultra-high intensity chirped lasers. This model is also feasible in that case.

Figure 3a shows the maximum electron energy (γ_m) with the crossing angle of the chirped lasers for different laser intensity parameters a₀ = 3, 7, and 10. In the case of chirped lasers, the electron energy is maximized at a crossing angle θ = 0.06 radian. This is because of the intensity maxima in constructive interference. The maximum electron energy decreases due to the changing in crossing angle. Figure 3b shows the same for un-chirped lasers. The electron gains maximum energy for a crossing angle of θ = 0.1 radian for un-chirped lasers.

Electron energy γ as a function of crossing angle θ (in radian) (a) with a frequency chirp and (b) without a frequency chirp for different values of the normalized laser amplitude. Other parameters are same as used in Figure 1.

In order to achieve the desired high-energy gains in a vacuum, a study of electron dynamics need to be conducted in the higher laser fields. The required fields can be realized by using two crossed lasers of low-intensities because of the constructive interference. One may achieve a high field for this purpose by using a single lasers but very high laser intensity (≥ 10²² Wcm⁻²) is required. Hence, the proposed scheme is purposeful and more convenient for available laser technology. Recently, Singh (2005) used a single chirped laser pulse for a vacuum electron acieration. The electron energy gain is about 50 MeV for the laser intensity a₀ = 5 corresponding to a suitable frequency chirp (cf. Fig. 2a in Singh (2005)). In our case, where two crossed lasers are proposed for electron acceleration, the electron energy gain is about 250 MeV (five times more) for laser intensity a₀ = 3 (cf. Fig. 2a). By such an acceleration scheme, the electron can be accelerated to a very high energy.

In conclusion, we propose a scheme for the acceleration of an externally injected electron by crossing two lasers of finite spot size in a vacuum by introducing the concept of frequency chirping. The resultant field of the lasers accelerates the electron to high energy. For an energy intensity parameter value a₀, a crossing angle θ exists which optimizes the electron energy due to the constructive interference. A suitable frequency chirp enhances the electron momentum and the electron escapes from the laser pulse near the peak to gain higher energy. The net energy gain is much higher with frequency chirp than that without frequency chirp. The frequency chirp not only enhances the energy of the electron but also retains it up to a long distance after passing of the laser pulses. The high efficiency chirped laser pulse can be generated by using a plasma Bragg grating induced by two lasers. Recently, Wu et al. (2005) shown that plasma Bragg grating is a novel element for this purpose.