1. INTRODUCTION
Electron acceleration has been the subject of research for many decades due to its wide applications ranging from high-energy physics to highly sensitive physical and chemical analyses (Yatsui, Reference Yatsui1989). Tajima and Dawson (Reference Tajima and Dawson1979) analyzed that a laser beam propagating in plasma can excite electron plasma wave, which can be used to accelerate electrons. Since then tremendous progress is achieved, theoretically as well as experimentally in the laser-plasma interaction-based accelerators (Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakajima, Masuda, Ho, Miyanaga, Limpouch and Andreev2005; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006). The table top terawatt laser accelerators based on the chirped-pulse amplification technique are capable of producing high-energy electrons/protons in much shorter distances than the conventional accelerators due to the large electric fields, associated with lasers (Perry & Mourou, Reference Perry and Mourou1994; Hora et al., Reference Hora, Hoelss, Scheid, Wang, Ho, Osman and Castillo2000). The schemes of laser beat wave acceleration and laser wakefield acceleration have been studied rigorously in past two decades and electron acceleration upto GeV has been achieved using these schemes (Dawson, Reference Dawson1959; Hafizi et al., Reference Hafizi, Ting, Esarey, Sprangle and Krall1997; Tomassini et al., Reference Tomassini, Galimberti, Giulietti, Giulietti, Gizzi, Labate and Pegoraro2004; Tochitsky et al., Reference Tochitsky, Narang, Filip, Musumeci, Clayton and Yoder2004; Jha et al., Reference Jha, Saroch and Mishra2013). However, in these accelerators, the laser intensities are very large (sometimes ultra-high laser intensities) due to which the accelerated electron energy is very high. The low-energy particle beams are expected to be useful for a wide range of contexts, including proton therapy for the treatment of cancers, materials characterization, radiation-driven chemistry, and in security application through the detection of explosives and narcotics.
One of the methods to generate well-behaved electron beams having low energy is electron acceleration by a surface plasma wave (SPW). This phenomenon was discovered recently and it was experimentally demonstrated that it is suitable for the production of relatively low-energy, quasi-monoenergetic electron beams with the usage of femtosecond lasers (Kupersztych et al., Reference Kupersztych, Monchicourt and Raynaud2001; Irvine et al., Reference Irvine, Dechant and Elezzabi2004; Liu et al., Reference Liu, He and Hora2005). In this scheme, the evanescent electric field of surface plasmon polaritons accelerates photo-emitted electrons away from the surface. Zawadzka et al. (Reference Zawadzka, Jaroszynski, Carey and Wynne2000) used 150 fs, 6 µJ (21 GW/cm2) laser pulses to excite SPWs using the Kretschmann configuration and demonstrated 40 eV electron production. In their follow-up experiments, 400 eV electrons were generated by exciting the SPWs with 0.8 mJ (40 TW/cm2) laser pulses (Zawadzka et al., 2001). Kalmykov et al. (Reference Kalmykov, Polomarov, Korobkin, Otwinowski, Power and Shvets2006) have studied SPW excitation on two parallel plane silicon carbide films separated by a vacuum region and discussed its potential for electron acceleration. Steinhauer and Kimura (Reference Steinhauer and Kimura2003) developed an elegant analytical formalism for surface wave propagation over two parallel conducting planes and on the inner boundary of a hollow cylinder to describe the potential of SPW for electron acceleration. Later, Liu et al. (Reference Liu, Kumar, Singh and Tripathi2007) used double-metal surface configuration separated by a vacuum region for studying electron acceleration, employing resonant interaction of electrons with SPW and achieved accelerating electrons up to tens of KeV energy. Dieckmann et al. (Reference Dieckmann, Ljung, Ynnerman and Mcclements2002) examined electron acceleration by an electrostatic plasma wave in magnetized plasma. This energy of accelerated electrons can be further regulated by applying external magnetic field. An optimum static magnetic field should be applied to continuously accelerate electrons before entering the deceleration phase. The electron can gain and retain a significant energy in the form of cyclotron oscillations in the presence of a static magnetic field (Gupta & Suk, Reference Gupta and Suk2006; Sajal & Tripathi, Reference Sajal and Tripathi2008; Gupta et al., Reference Gupta, Gopal, Nam, Kulagin and Suk2014).
In this paper, we have studied the effect of static magnetic field applied in the direction of propagation of SPW on electron beam acceleration. To study this effect, we have used the configuration of two parallel metal surfaces that supports SPW having amplitude maxima on the two surfaces and minimum in the middle. This mode can be excited by shining a laser on the glass prism using the Kretschmann geometry Neuner et al. (Reference Neuner, Korobkin, Ferro and Shvets2012). The static magnetic field is applied in the direction of propagation of SPW, that is, in the ![]() $\hat z$-direction. When the axial velocity of the electron beam is comparable with that of the phase velocity of the surface wave, it can gain large energies from the wave. The applied magnetic field may be useful for accelerating electrons to achieve desired energies of moderate range with the control in their trajectories. The dispersion relation of SPW in double-metal surface configuration has been derived in Section 1 and electron acceleration by SPW has been discussed in Section 3. In Section 4, we have discussed the results and the conclusions in Section 5.
$\hat z$-direction. When the axial velocity of the electron beam is comparable with that of the phase velocity of the surface wave, it can gain large energies from the wave. The applied magnetic field may be useful for accelerating electrons to achieve desired energies of moderate range with the control in their trajectories. The dispersion relation of SPW in double-metal surface configuration has been derived in Section 1 and electron acceleration by SPW has been discussed in Section 3. In Section 4, we have discussed the results and the conclusions in Section 5.
2. SPW IN DOUBLE-METAL SURFACE CONFIGURATION
Consider two parallel metal half-spaces x < −a/2 and x > a/2 separated by a vacuum −a/2 < x< a/2 as shown in Figure 1. The SPW propagates along the ![]() $\hat z$-direction in this system. The electrons to be accelerated are injected in the center of the vacuum region and external axial magnetic field
$\hat z$-direction in this system. The electrons to be accelerated are injected in the center of the vacuum region and external axial magnetic field ![]() $\vec B_s $ is applied in the
$\vec B_s $ is applied in the ![]() $\hat z$-direction. In this case, the effective permittivity
$\hat z$-direction. In this case, the effective permittivity ![]() $\lpar \tilde {\rm \varepsilon} \rpar $of the metal is a dielectric tensor with independent components, each one as a function of frequency and the plasma's characteristics (Miraboutalebi et al., Reference Miraboutalebi, Rajaee and Matin2012). It is given by
$\lpar \tilde {\rm \varepsilon} \rpar $of the metal is a dielectric tensor with independent components, each one as a function of frequency and the plasma's characteristics (Miraboutalebi et al., Reference Miraboutalebi, Rajaee and Matin2012). It is given by
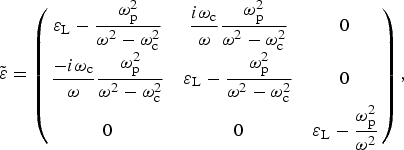 $$\tilde {\rm \varepsilon} = \left({\matrix{ {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & {\displaystyle{{i{\rm \omega}_{\rm c} } \over {\rm \omega} }\displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & 0 \cr {\displaystyle{{ - i{\rm \omega}_{\rm c} } \over {\rm \omega} }\displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & 0 \cr 0 & 0 & {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 }}} \cr } } \right)\comma \; $$
$$\tilde {\rm \varepsilon} = \left({\matrix{ {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & {\displaystyle{{i{\rm \omega}_{\rm c} } \over {\rm \omega} }\displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & 0 \cr {\displaystyle{{ - i{\rm \omega}_{\rm c} } \over {\rm \omega} }\displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 - {\rm \omega}_{\rm c}^2 }}} & 0 \cr 0 & 0 & {{\rm \varepsilon}_{\rm L} - \displaystyle{{{\rm \omega}_{\rm p}^2 } \over {{\rm \omega}^2 }}} \cr } } \right)\comma \; $$where εL is the lattice permittivity, ωp and ωc are the plasma and cyclotron frequency. ωc is computed as ωc = eB S/ m, where B s is the strength of externally applied static magnetic field. The electric field of the SPW propagating through this configuration varies as Tochitsky et al. (Reference Tochitsky, Narang, Filip, Musumeci, Clayton and Yoder2004). Maxwell's equations are used to study the dispersion relations of SPWs in this configuration.

Fig. 1. Configuration of a vacuum bounded by the two metal surfaces.
On eliminating ![]() $\vec B$ from Eqs (2) and (3), the wave equation can be found as
$\vec B$ from Eqs (2) and (3), the wave equation can be found as
Equation (4) can be expanded as follows:
 $$\displaystyle{{\partial ^2 E_x } \over {\partial x^2 }} - \left({k_z^2 - \displaystyle{{{\rm \omega}^2 } \over {c^2 }}{\rm \varepsilon}_{xx} } \right)E_x = 0\comma \; $$
$$\displaystyle{{\partial ^2 E_x } \over {\partial x^2 }} - \left({k_z^2 - \displaystyle{{{\rm \omega}^2 } \over {c^2 }}{\rm \varepsilon}_{xx} } \right)E_x = 0\comma \; $$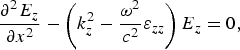 $$\displaystyle{{\partial ^2 E_z } \over {\partial x^2 }} - \left({k_z^2 - \displaystyle{{{\rm \omega}^2 } \over {c^2 }}{\rm \varepsilon}_{zz} } \right)E_z = 0\comma \; $$
$$\displaystyle{{\partial ^2 E_z } \over {\partial x^2 }} - \left({k_z^2 - \displaystyle{{{\rm \omega}^2 } \over {c^2 }}{\rm \varepsilon}_{zz} } \right)E_z = 0\comma \; $$where εxx = εL − ωp2/(ω2 − ωc2) for x > a/2 and x < − a/2 and εxx = 1 for −a/2 < x < a/2 and εzz = εL − ωp2/(ω2 for x > a/2 and x < −a/2, and εzz = 1 for −a/2 < x < a/2.
The electric field associated with the SPW [Eq. (5)] can be obtained by satisfying ![]() $\nabla .\tilde {{\rm \varepsilon}} E = 0$ in each region, which are given by
$\nabla .\tilde {{\rm \varepsilon}} E = 0$ in each region, which are given by
 $$E = \left[{\displaystyle{{ik_z } \over {{\rm \alpha}_1 }}\left({\displaystyle{{\lpar {\rm \omega}^2 - {\rm \omega}_{\rm p}^2 \rpar \lpar {\rm \omega}^2 - {\rm \omega}_{\rm c}^2 \rpar } \over {{\rm \omega}^2 \lpar {\rm \omega}^2 - {\rm \omega}_{\rm h}^2 \rpar }}} \right)\hat x+\hat z} \right]Ae^{ - {\rm \alpha} _1 x} .e^{ - i\lpar {\rm \omega} t - k_z z\rpar }\comma \; \quad \, \hbox{for}\, x\gt a/2\comma \; $$
$$E = \left[{\displaystyle{{ik_z } \over {{\rm \alpha}_1 }}\left({\displaystyle{{\lpar {\rm \omega}^2 - {\rm \omega}_{\rm p}^2 \rpar \lpar {\rm \omega}^2 - {\rm \omega}_{\rm c}^2 \rpar } \over {{\rm \omega}^2 \lpar {\rm \omega}^2 - {\rm \omega}_{\rm h}^2 \rpar }}} \right)\hat x+\hat z} \right]Ae^{ - {\rm \alpha} _1 x} .e^{ - i\lpar {\rm \omega} t - k_z z\rpar }\comma \; \quad \, \hbox{for}\, x\gt a/2\comma \; $$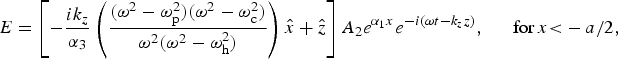 $$E = \left[{ - \displaystyle{{ik_z } \over {{\rm \alpha}_3 }}\left({\displaystyle{{\lpar {\rm \omega}^2 - {\rm \omega}_{\rm p}^2 \rpar \lpar {\rm \omega}^2 - {\rm \omega}_{\rm c}^2 \rpar } \over {{\rm \omega}^2 \lpar {\rm \omega}^2 - {\rm \omega}_{\rm h}^2 \rpar }}} \right)\hat x+\hat z} \right]A_2 e^{{\rm \alpha} _1 x} e^{ - i\lpar {\rm \omega} t - k_z z\rpar }\comma \; \quad \, \hbox{for}\, x{\rm\lt } - a/2\comma \; $$
$$E = \left[{ - \displaystyle{{ik_z } \over {{\rm \alpha}_3 }}\left({\displaystyle{{\lpar {\rm \omega}^2 - {\rm \omega}_{\rm p}^2 \rpar \lpar {\rm \omega}^2 - {\rm \omega}_{\rm c}^2 \rpar } \over {{\rm \omega}^2 \lpar {\rm \omega}^2 - {\rm \omega}_{\rm h}^2 \rpar }}} \right)\hat x+\hat z} \right]A_2 e^{{\rm \alpha} _1 x} e^{ - i\lpar {\rm \omega} t - k_z z\rpar }\comma \; \quad \, \hbox{for}\, x{\rm\lt } - a/2\comma \; $$
where ωh2 = ωp2 + ωc2, α1 = (k z2 − ω2 εzz/c 2)1/2, α2 = (k z2 − ω2/c 2)1/2, and α3 = (k z2 − ω2 εxx/c 2)1/2. A, A 1, A′1, and A 2 are constants. E z and ![]() $\tilde{{\rm \varepsilon}} E_x $ are continuous at the two interfaces x = a/2 and x = −a/2, which provides
$\tilde{{\rm \varepsilon}} E_x $ are continuous at the two interfaces x = a/2 and x = −a/2, which provides
On eliminating A, A 1, A′1, and A 2, we obtain the dispersion relation of the SPW in the presence of external magnetic field as
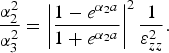 $$\displaystyle{{{\rm \alpha} _2^2 } \over {{\rm \alpha} _3^2 }} = \left\vert {\displaystyle{{1 - e^{{\rm \alpha}_2 a} } \over {1+e^{{\rm \alpha}_2 a} }}} \right\vert ^2 \displaystyle{1 \over {{\rm \varepsilon} _{zz}^2 }}.$$
$$\displaystyle{{{\rm \alpha} _2^2 } \over {{\rm \alpha} _3^2 }} = \left\vert {\displaystyle{{1 - e^{{\rm \alpha}_2 a} } \over {1+e^{{\rm \alpha}_2 a} }}} \right\vert ^2 \displaystyle{1 \over {{\rm \varepsilon} _{zz}^2 }}.$$ Equation (8) is normalized using dimensionless quantities q = k zc/ωp, Ω = ω/ωp, Ωc = ωc/ωp, and width of vacuum gap(a) is a′ = aωp/c. Figure 2 depicts the variation of the normalized distance between the metal plates (aωp/c) versus electric field of SPW in the vacuum region for k zc/ωp = 0.05. It is observed that the surface plasma modes exist on both metal surfaces with electric field minimum in the center and maximum on the two surfaces. Figure 3 shows variation of (ω/ωp) versus (k zc/ω) on the varying normalized cyclotron frequency (ωc/ωp) for the mode that has E x symmetric about x = 0 (A 1 = A′1). The parameters are a′ = 100 and εL = 1. Recently, Liu et al. (Reference Liu, Kumar, Singh and Tripathi2007) obtained dispersion relation of SPWs for double-metal surface configuration and observed linear increase in the frequency of SPWs with the wavenumber and it saturates at higher value of wavenumber that is, the wave propagates with frequencies ranging from zero at (k zc/ωp = 0) toward the asymptotic value ![]() $\lpar {\rm \omega} = {\rm \omega} _{\rm p} /\sqrt 2 \rpar $. In the presence of external magnetic field, the dispersion curve consists of two parts with a gap between them. One of the branches occurs at a higher frequency and the other at a lower frequency as shown in Figure 3. In the lower portion, the cut-off frequency occurs at ω = ωc and increases with the increase in cyclotron frequency. In the upper portion, the cut-off frequency decreases (enlarged view is shown in Figure 3b as the cyclotron frequency is varied from 0.05 to 0.2. Similar behavior is observed by Brion et al. (Reference Brion, Wallis, Hartstein and Burstein1972) and Chiu and Quinn (Reference Chiu and Quinn1972). We have studied electron acceleration for the lower portion at k zc/ωp = 0.04. Figure 4 enveals the disersion relation of SPW on the varying distance between the two metal plates for (ωc/ωp) = 0.2 and εL = 1. It is observed that there is no effect on the dispersion characteristics of the SPWs with distance between the metal plates (Kumar et al., Reference Kumar, Kumar and Tripathi2010).
$\lpar {\rm \omega} = {\rm \omega} _{\rm p} /\sqrt 2 \rpar $. In the presence of external magnetic field, the dispersion curve consists of two parts with a gap between them. One of the branches occurs at a higher frequency and the other at a lower frequency as shown in Figure 3. In the lower portion, the cut-off frequency occurs at ω = ωc and increases with the increase in cyclotron frequency. In the upper portion, the cut-off frequency decreases (enlarged view is shown in Figure 3b as the cyclotron frequency is varied from 0.05 to 0.2. Similar behavior is observed by Brion et al. (Reference Brion, Wallis, Hartstein and Burstein1972) and Chiu and Quinn (Reference Chiu and Quinn1972). We have studied electron acceleration for the lower portion at k zc/ωp = 0.04. Figure 4 enveals the disersion relation of SPW on the varying distance between the two metal plates for (ωc/ωp) = 0.2 and εL = 1. It is observed that there is no effect on the dispersion characteristics of the SPWs with distance between the metal plates (Kumar et al., Reference Kumar, Kumar and Tripathi2010).

Fig. 2. Variation of the normalized distance between the metal plates (a′ = aω p/c) versus electric field of SPW.

Fig. 3. (a) Variation of the normalized frequency (ω/ω p) versus normalized wave number (k zc/ωp). (b) Enlarged view of Figure 3a.

Fig. 4. Plot of dispersion relation of SPW on the varying distance between the metal plates (a′ = aωp/c) for ωc/ωp=0.2.
3. ELECTRON ACCELERATION IN THE PRESENCE OF A MAGNETIC FIELD
An electron beam is launched in the central region in the ![]() $\hat z$-direction and static magnetic field
$\hat z$-direction and static magnetic field ![]() $\vec B_s $ is applied in the same direction. This electron beam interacts with the wave of large amplitude in the central region (E z ≅ 2.4 × 1011 V/m at x = 0 as shown in Fig. 2). Although the field strength is less at the two interfaces, it is still sufficient for the electron acceleration. Zawadzka et al. (Reference Zawadzka, Jaroszynski, Carey and Wynne2001) reported that electric field amplitude of the order of 109 V/m can be used to accelerate electrons. Now, the motion of electrons is goverened by two fields, the electric field due to SPWs and the externally applied static magnetic field. The electron response is goverened by the equation of motion
$\vec B_s $ is applied in the same direction. This electron beam interacts with the wave of large amplitude in the central region (E z ≅ 2.4 × 1011 V/m at x = 0 as shown in Fig. 2). Although the field strength is less at the two interfaces, it is still sufficient for the electron acceleration. Zawadzka et al. (Reference Zawadzka, Jaroszynski, Carey and Wynne2001) reported that electric field amplitude of the order of 109 V/m can be used to accelerate electrons. Now, the motion of electrons is goverened by two fields, the electric field due to SPWs and the externally applied static magnetic field. The electron response is goverened by the equation of motion
where –e, m, and ![]() $\vec v$ are the electronic charge, mass, and velocity of the electron, respectively. We can replace the magnetic field of SPW by
$\vec v$ are the electronic charge, mass, and velocity of the electron, respectively. We can replace the magnetic field of SPW by
Equation (9) is solved for x, y, and z-components of momentum of electron, which are given as
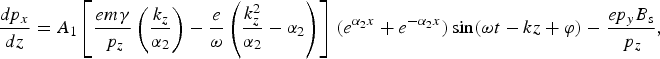 $$\displaystyle{{dp_x } \over {dz}}=A_1 \left[{\displaystyle{{em{\rm \gamma} } \over {\,p_z }}\left({\displaystyle{{k_z } \over {{\rm \alpha}_2 }}} \right)- \displaystyle{e \over {\rm \omega} }\left({\displaystyle{{k_z^2 } \over {{\rm \alpha}_2 }} - {\rm \alpha}_2 } \right)} \right]\, \lpar e^{{\rm \alpha} _2 x}+e^{ - {\rm \alpha} _2 x} \rpar \sin \lpar {\rm \omega} t - kz+{\rm \varphi} \rpar - \displaystyle{{ep_y B_{\rm s} } \over {\,p_z }}\comma \; $$
$$\displaystyle{{dp_x } \over {dz}}=A_1 \left[{\displaystyle{{em{\rm \gamma} } \over {\,p_z }}\left({\displaystyle{{k_z } \over {{\rm \alpha}_2 }}} \right)- \displaystyle{e \over {\rm \omega} }\left({\displaystyle{{k_z^2 } \over {{\rm \alpha}_2 }} - {\rm \alpha}_2 } \right)} \right]\, \lpar e^{{\rm \alpha} _2 x}+e^{ - {\rm \alpha} _2 x} \rpar \sin \lpar {\rm \omega} t - kz+{\rm \varphi} \rpar - \displaystyle{{ep_y B_{\rm s} } \over {\,p_z }}\comma \; $$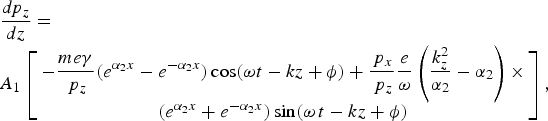 $$\eqalign{& \displaystyle{{dp_z } \over {dz}} =\cr& A_1 \left[\matrix{ - \displaystyle{{me{\rm \gamma} } \over {\,p_z }}\lpar e^{{\rm \alpha}_2 x} - e^{ - {\rm \alpha}_2 x} \rpar \cos \lpar {\rm \omega} t - kz+{\rm \phi} \rpar +\displaystyle{{\,p_x } \over {\,p_z }}\displaystyle{e \over {\rm \omega} }\left({\displaystyle{{k_z^2 } \over {{\rm \alpha}_2 }} - {\rm \alpha}_2 } \right)\times \cr \lpar e^{{\rm \alpha}_2 x}+e^{ - {\rm \alpha}_2 x} \rpar \sin \lpar {\rm \omega} \, t - kz+{\rm \phi} \rpar } \right]\comma \;} $$
$$\eqalign{& \displaystyle{{dp_z } \over {dz}} =\cr& A_1 \left[\matrix{ - \displaystyle{{me{\rm \gamma} } \over {\,p_z }}\lpar e^{{\rm \alpha}_2 x} - e^{ - {\rm \alpha}_2 x} \rpar \cos \lpar {\rm \omega} t - kz+{\rm \phi} \rpar +\displaystyle{{\,p_x } \over {\,p_z }}\displaystyle{e \over {\rm \omega} }\left({\displaystyle{{k_z^2 } \over {{\rm \alpha}_2 }} - {\rm \alpha}_2 } \right)\times \cr \lpar e^{{\rm \alpha}_2 x}+e^{ - {\rm \alpha}_2 x} \rpar \sin \lpar {\rm \omega} \, t - kz+{\rm \phi} \rpar } \right]\comma \;} $$where γ = (1 + (p x2 + p y2 + p z2/m 2c 2))1/2 and ϕ is the initial phase of the wave. These equations are supplemented with
The sets of Eqs (10)–(15) are normalized by introducing dimensionless quantities A 1″ → eA 1/mωpc, X → ωpx/c, Y → ωpy/c, Z → ωpz/c, P x → p x/mc, P y → p y/mc, P z → p z /mc, T → ωpt, Ω → ω/ωp, Ωc → ωc/ωp, and q → k zc/ωp and are solved numerically for the electron energy and electron trajectory. The parameters are P x(0) = 0.01, P y(0) = 0.01, P z(0) = 0.09, x(0) = 0.01, y(0) = 0.01, t(0) = 0.0, ϕ = π/2, E SP = 1.2 × 1011 V/m, ωp = 1.3 × 1016 rad/s, and the width of vacuum gap is a = 231 µm, that is, (aωp/c) = 100. The parameters used for this numerical analysis, are in agreement with the parameters used in the experimental and analytical studies by Zawadzka et al. (Reference Zawadzka, Jaroszynski, Carey and Wynne2001), Liu et al. (Reference Liu, Kumar, Singh and Tripathi2007), Neuner et al. (Reference Neuner, Korobkin, Ferro and Shvets2012), and Kumar et al. (Reference Kumar, Kumar and Tripathi2010). The kinetic energy gained by electrons with normalized distance have been ploted in Figure 5, with and without magnetic field. Figure 6 shows the effect of amplitude variation on electron energy. Trajectory of the electron beam has been plotted in Figures 7 and 8, respectively, on the varying magnetic field and amplitude of the wave.

Fig. 5. Plot of kinetic energy (γ/2) in KeV gained by electron versus normalized distance (zω p/c) on the varying strength of the magnetic field.

Fig. 6. Plot of kinetic energy (γ/2) in KeV gained by electron versus normalized distance (zωp/c) for (ωc/ωp) = 0.2 on the varying amplitude of SPW.

Fig. 7. Trajectory of the accelerated electron versus normalized distance on the varying strength of the magnetic field.

Fig. 8. Trajectory of the accelerated electron on the varying strength of the magnetic field.
4. RESULTS AND DISCUSSION
In Figure 5, we have plotted the energy (in KeV) gained by the electrons versus normalized distance (zωp/c) for the increasing values of the normalized cyclotron frequency (ωc/ωp). It is observed that the electron acceleration is higher in the presence of an external magnetic field as compared with that of without magnetic field. We have obtained electrons of energy ≈550 KeV for the cylotron frequency (ωc/ωp) = 0.05. On increasing (ωc/ωp) to 0.1, energy gained by electrons decreases to 512 KeV as compared with its values for (ωc/ωp) = 0.05, which is larger as compared with energy (≈502 KeV) when the external magnetic field is zero. Electron gains energy during the rising part of the pulse and loses it during the trailing part, resulting in negligible energy gain. The presence of static magnetic field not only leads to the enhancement of the energy gain, but also to the retention of most of the energy in the form of cyclotron oscillations. The launched electron experiences a V × B force, which deviates it away from the axis either in the ![]() $+\hat x$ or
$+\hat x$ or ![]() $ - \hat x$-direction, strikes the metal–vacuum interface (as shown in Fig. 7) and gains very small energy. On introducing external magnetic field, electron experiences another V × B s force. This force prevents the electrons from escaping the SPW field and faces higher values of SPW amplitude, as it has maximum values at the two interfaces and minimum in the middle. The energy gained by the electron beam is more in the presence of an external field as compared with that of without field. With the increase in the strength of field, the electrons turn toward the z-axis more effectively and repeatedly, faces smaller values of SPW amplitude and hence their gain reduces. However, the gain is still more as compared with the energy gain in the absence of magnetic field. These results can be explained by Figure 5. In Figure 6, we have plotted energy (in KeV) gained by the electrons versus normalized distance (zωp/c) for different values of SPW amplitude at (ωc/ωp) = 0.2. Energy gained by electron increases with the amplitude of SPW. Electron beam of energy ~550 KeV is obtained for SPW amplitude eA 1/mωpc = 0.02164. Energy gained by electron beam decreases on decreasing the amplitude of SPW by two times, that is, for 0.01082 and 0.00541. The trajectories of the accelerated electrons launched in the center of the vacuum region are plotted in Figures 7–9. It is observed in Figure 7 that when (ωc/ωp) = 0, the electron beam travels along x = 0, that is, in straight line for the smaller values of zωp/c≃4 [Figure 7 of Liu et al. (Reference Liu, Kumar, Singh and Tripathi2007)] and diverges strongly for the higher values of normalized distance. In the presence of external magnetic field, the electron experience V × B s force and converges toward the positive z-axis. The electron beam converges more and more in the
$ - \hat x$-direction, strikes the metal–vacuum interface (as shown in Fig. 7) and gains very small energy. On introducing external magnetic field, electron experiences another V × B s force. This force prevents the electrons from escaping the SPW field and faces higher values of SPW amplitude, as it has maximum values at the two interfaces and minimum in the middle. The energy gained by the electron beam is more in the presence of an external field as compared with that of without field. With the increase in the strength of field, the electrons turn toward the z-axis more effectively and repeatedly, faces smaller values of SPW amplitude and hence their gain reduces. However, the gain is still more as compared with the energy gain in the absence of magnetic field. These results can be explained by Figure 5. In Figure 6, we have plotted energy (in KeV) gained by the electrons versus normalized distance (zωp/c) for different values of SPW amplitude at (ωc/ωp) = 0.2. Energy gained by electron increases with the amplitude of SPW. Electron beam of energy ~550 KeV is obtained for SPW amplitude eA 1/mωpc = 0.02164. Energy gained by electron beam decreases on decreasing the amplitude of SPW by two times, that is, for 0.01082 and 0.00541. The trajectories of the accelerated electrons launched in the center of the vacuum region are plotted in Figures 7–9. It is observed in Figure 7 that when (ωc/ωp) = 0, the electron beam travels along x = 0, that is, in straight line for the smaller values of zωp/c≃4 [Figure 7 of Liu et al. (Reference Liu, Kumar, Singh and Tripathi2007)] and diverges strongly for the higher values of normalized distance. In the presence of external magnetic field, the electron experience V × B s force and converges toward the positive z-axis. The electron beam converges more and more in the ![]() $\hat z$-direction on increasing (ωc/ωp) from 0.05 to 0.1 as shown in Figure 8. In the absence of magnetic field, the divergence of electron trajectory is much higher. Amplitude of SPW also affects electron trajectory significantly as shown in Figure 9.
$\hat z$-direction on increasing (ωc/ωp) from 0.05 to 0.1 as shown in Figure 8. In the absence of magnetic field, the divergence of electron trajectory is much higher. Amplitude of SPW also affects electron trajectory significantly as shown in Figure 9.

Fig. 9. Trajectory of the accelerated electron on increasing amplitude of SPWs when (ωc/ωp) = 0.2 and (ωc/ωp) = 0.0.
5. CONCLUSIONS
Electron acceleration at moderate relative intensity by SPW excited with double-metal surface configuration shows a significant promise. The double-metal structure helps in guiding the electron beam without diverging it as the field of SPW is maximum at the two interfaces and minimum at the center. The electron beam injected in the center of the vacuum region follows nearly a straight line path in the absence of magnetic field, do not return to the axis and gains very small energy. An electron moving away from the ![]() $\hat z$-axis either in the
$\hat z$-axis either in the ![]() $+\hat x$ or
$+\hat x$ or ![]() $ - \hat x$-direction in the presence of magnetic field will experience a V × B s force along the positive
$ - \hat x$-direction in the presence of magnetic field will experience a V × B s force along the positive ![]() $\hat z$-direction. This force prevents the electrons from escaping the SPW field and the electron returns to the axial points, hence gains energy. With an increase in strength of the magnetic field, the electrons turn toward the z-axis more effectively and repeatedly and gains less energy as it encounters lesser values of SPW amplitude in the central region. On increasing the amplitude of SPW, energy gain and trajectory of the accelerated electrons are further improved.
$\hat z$-direction. This force prevents the electrons from escaping the SPW field and the electron returns to the axial points, hence gains energy. With an increase in strength of the magnetic field, the electrons turn toward the z-axis more effectively and repeatedly and gains less energy as it encounters lesser values of SPW amplitude in the central region. On increasing the amplitude of SPW, energy gain and trajectory of the accelerated electrons are further improved.
In conclusion, as the energy gained by the electron beam increases on applying external magnetic field as well as is affected by SPW amplitude and the electron trajectory is also connected with these two parameters, one can get a well-behaved moderate energy gain with controlled trajectory by optimizing these external parameters. This scheme is viable to achieve the beams of KeV energy for the optimum values of magnetic field and SPW amplitude.



