1. INTRODUCTION
In last few years, Terahertz (THz) radiation generation (Dua et al., Reference Dua, Chena, Shenga and Zhanga2011; Hu et al., Reference Hu, Shen, Lei, Li and Xu2010; Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Jia2010; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013) has attracted a lot of interest due to its potential applications in material characterization, imaging, topography, remote sensing, chemical and security identification, explosive detection, outer space communication, etc. (Ferguson et al., Reference Ferguson and Zhang2002; Shen et al., Reference Shen, Today, Cole, Tribe and Kemp2005; Zheng et al., Reference Zheng, Redo-Sanchez and Zhang2006; Pickwell et al., Reference Pickwell and Wallace2006; Antonsen et al., Reference Antonsen, Palastra and Milchberg2007; Liu et al., Reference Liu and Tripathi2009; Malik et al., Reference Malik, Malik and Kawata2010). Conventional methods employing electro-optic crystals and semiconductors are not efficient enough to achieve high energy pulses of THz radiation (Faure et al., Reference Faure, Tilborg, Kaindl and Leemans2004; Shi et al., Reference Shi, Ding, Fernelius and Vodopyanov2002; Zhao et al., Reference Zhao, Ragam, Ding and Zotova2010) due to their lower damage limit. To achieve this objective, plasma is utilized as a nonlinear medium in various schemes (Kumar et al., Reference Kumar and Tripathi2013; Giulietti et al., Reference Giulietti, Banfi, Deha, Giulietti, Lucchesi, Nocera and Zun1988; Panwar et al., Reference Panwar, Ryu and Kumar2013; Garg et al., Reference Garg and Tripathi2010; Ghorbanalilu et al., Reference Ghorbanalilu2012; Verma et al., Reference Verma and Sharma2009) employing a strong laser plasma interaction (Verma et al., Reference Verma and Sharma2011; Paknezhad et al., Reference Paknezhad and Dorranian2011) because plasma can handle very high power lasers and it has an added advantage of not having damage limit (Jiang et al., Reference Jiang, Li, Ding and Zotova2011; Leemans et al., Reference Leemans, Tilborg, Faure, Geddes, Toth, Schroeder, Esarey, Fubioni and Dugan2004; Pukhov et al., Reference Pukhov2003; Hashimshony et al., Reference Hashimshony, Zigler and Papadopoulos1999; Tani et al., Reference Tani, Gu, Hyodo, Sakai and Hidaka2000; Loffler et al., Reference Loffler, Kress, Thomson and Roskos2005; Breunig et al., Reference Breunig, Kiessling, Sowade, Knabe and Buse2008). Out of various schemes proposed in the literature, THz pulse energy achieved from laser filaments is quite high (Wang et al., Reference Wang, Daigle, Yuan, Theberge, Chateauneuf, Dubois, Roy, Zeng and Chin2011; Ladouceur et al., Reference Ladouceur, Baronavski, Lohrmann, Grounds and Girardi2001; Tripathi et al., Reference Tripathi and Liu1990; Loffler et al., Reference Loffler, Jacbo and Roskos2000; Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008) as compared to other schemes like coherent radiation from plasma oscillations driven by ultra-short laser pulses (Hamster et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993; Reference Hamster, Sullivan, Gordon and Falcone1994), synchrotron radiation from accelerated electrons (Carr et al., Reference Carr, Martin, Mckinney, Jordan, Neil and Williams2002), the transition radiation of electron beams (Abo-Bakar et al., Reference Abo-Bakr, Feikes, Holldack, Kuske, Peatman, Schade, Wustefeld and Hübers2003), etc. Wang et al. (Reference Wang, Daigle, Yuan, Theberge, Chateauneuf, Dubois, Roy, Zeng and Chin2011) have experimentally observed 570 nJ THz pulse energy at frequency ≤5.5 THz, at a distance of ~ 10 m by two color femtosecond filamentation in air.
Ladouceur et al. (Reference Ladouceur, Baronavski, Lohrmann, Grounds and Girardi2001) were among the first to observe broadband THz radiation employing the plasma filaments (electron density ~1016 m−3 at 0.9 THz plasma frequency) formed through multi-photon ionization by a 100 fs laser pulse propagating in air and achieved power conversion efficiency of ~10−9. Tripathi et al. (Reference Tripathi and Liu1990) investigated THz radiation generation in air via bi-filamentation of two co-propagating femtosecond laser pulses with suitable time delay. For a time delay of less than 2 ns, the amplitude of 0.1 THz frequency radiation was found to be 10 times higher than the one due to a single pulse. However, for other frequencies, it could be greater or less than 10. When a femtosecond laser pulse propagates through air, it undergoes filamentation and self-focusing and forms the plasma channel which, attains strong dipole moment and emits electromagnetic radiation. The radiation frequency can be controlled and maintained in the THz range by choosing suitable plasma parameters.
Loffler et al. (Reference Loffler, Jacbo and Roskos2000) reported a large enhancement of intensity of THz radiation emitted by ionized air in the presence of a static electric field. They observed a current surge following photo-ionization of the air with an applied bias field of 10.6 KV/cm leading to the emission of THz pulses with an intensity which can be almost as high as that of THz pulses radiated from a large-area intrinsic-field GaAs emitter. Recently, Houard et al. (Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008) observed a three order of magnitude of enhancement of the THz energy radiated by a femtosecond pulse undergoing filamentation in air in the presence of static electric field. The emitted THz wave was found to be linearly polarized in the plane containing the static electric field. They also provided a theoretical model which predicts that the total emitted energy is proportional to the square of the filament cross-section, square of direct current (dc) electric field, filament length, and plasma density in the channel in the power 3/2. Bhasin et al. (Reference Bhasin and Tripathi2011) also studied the THz radiation generation from laser filament in the presence of a static electric field in plasma. They observed an enhancement in coupling in the presence of the static electric field. The ratio of THz amplitude to that of filament amplitude is the order of 10−5 at laser intensities ~1014 W/cm2.
The THz amplitude obtained by the scheme proposed by Bhasin et al. (Reference Bhasin and Tripathi2011) can be improved many times by considering more realistic Gaussian profile of laser filaments. In the present work, we have studied the combined effects of Gaussian profile, static electric field, and filamented nature of lasers on THz radiation generation by beating of two co-propagating laser beams in plasma (Fig. 1). Transverse amplitude modulated lasers exert not only a nonlinear ponderomotive force F pω at beat frequency (ω) but a space periodic ponderomotive force F pq, which in association with gradient force produces transverse density ripples (of zero frequency and wave number ![]() $\vec q$) in the plasma. Plasma electrons, oscillated under the influence of beat frequency ponderomotive force give rise to density perturbation at frequency ω and wave number
$\vec q$) in the plasma. Plasma electrons, oscillated under the influence of beat frequency ponderomotive force give rise to density perturbation at frequency ω and wave number ![]() $\vec k$ as well as
$\vec k$ as well as ![]() $\vec k + \vec q$. Density perturbations couple with drift velocity
$\vec k + \vec q$. Density perturbations couple with drift velocity ![]() $\lpar {\vec {\rm \nu}_{dc}}\rpar $ due to static electric field in rippled plasma and produce a nonlinear current at frequency ω and wave number
$\lpar {\vec {\rm \nu}_{dc}}\rpar $ due to static electric field in rippled plasma and produce a nonlinear current at frequency ω and wave number ![]() $\vec k + \vec q$ which is responsible for THz radiation generation at resonance. In Section 2, expressions for the ponderomotive force, density perturbation, and nonlinear current responsible for THz generation are derived and the wave equation for THz wave is solved to calculate its amplitude. Conclusions are given in Section 3.
$\vec k + \vec q$ which is responsible for THz radiation generation at resonance. In Section 2, expressions for the ponderomotive force, density perturbation, and nonlinear current responsible for THz generation are derived and the wave equation for THz wave is solved to calculate its amplitude. Conclusions are given in Section 3.

Fig. 1. Schematic diagram of beat excitation of THz radiation in the presence of transverse static electric field ![]() ${\vec E_{dc}}$.
${\vec E_{dc}}$.
2. THZ RADIATION GENERATION DUE TO LASER BEATING
Consider two transversely modulated Gaussian laser beams co-propagating through the pre-existing plasma having electron plasma density n 00. The field profile of lasers is given by
where ![]() ${E_{\,j0}} = {A_{\,j0}}{e^{ - {y^2}/a_0^2 }}$; μj is the index of modulation, a 0 is the beam width, and q is the periodicity parameter. Dispersion relation of beating lasers is
${E_{\,j0}} = {A_{\,j0}}{e^{ - {y^2}/a_0^2 }}$; μj is the index of modulation, a 0 is the beam width, and q is the periodicity parameter. Dispersion relation of beating lasers is ![]() $k_j^2 = \lpar {{{\rm \omega} _j^2 } / {{c^2}}}\rpar \lcub 1 - {{\lpar {\rm \omega} _p^2 } / {{\rm \omega} _j^2 }}\rpar \rcub $. The frequency difference of the lasers ω = ω1 − ω2 lies in the THz range. The laser filaments impart oscillatory velocities to plasma electrons, given by
$k_j^2 = \lpar {{{\rm \omega} _j^2 } / {{c^2}}}\rpar \lcub 1 - {{\lpar {\rm \omega} _p^2 } / {{\rm \omega} _j^2 }}\rpar \rcub $. The frequency difference of the lasers ω = ω1 − ω2 lies in the THz range. The laser filaments impart oscillatory velocities to plasma electrons, given by
 $${\vec {\rm \nu}_j} = \displaystyle{{e{{\vec E}_{\,j0}}} \over {mi{{\rm \omega} _j}}}.$$
$${\vec {\rm \nu}_j} = \displaystyle{{e{{\vec E}_{\,j0}}} \over {mi{{\rm \omega} _j}}}.$$
The plasma is embedded with a dc electric field ![]() ${\vec E_{dc}}\Vert \hat x$ which provides dc velocity component to plasma electrons
${\vec E_{dc}}\Vert \hat x$ which provides dc velocity component to plasma electrons
where −e, m, and ν e are the charge, mass, and collision frequency of plasma electrons. Here, Debye shielding related aspects can be considered by assuming that plasma is formed by focusing Ti:Sa CPA (chirped pulse amplified) laser beam on hydrogen gas or air (Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008). The created plasma filament is modeled by specific electric field profile of beating laser given by Eq. (1). When external static electric field ![]() ${\vec E_{dc}}$ is applied across the plasma filament by placing two copper plane electrodes, plasma electrons start moving under the influence of the field. The charge is accumulated at the edge of filament and electric field is completely screened in the plasma. However, there is a transient process of redistribution of charges, and the temporal behavior of the electric current depends on relation between three parameters: the duration of the ionization process t ion, the electron collision time t col and the period of plasma oscillations. For typical laser pulse duration of 50 fs, the electron plasma density will be ~1016 cm−3 in a filament of radii 30–50 µm. Then, plasma period is approximately 1 ps, the collision time is ~100 ps; both of them longer than ionization time. Therefore one can consider the response of plasma with an instantaneous ionization, and the electric current which is directed along the direction of the external electric field (Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008).
${\vec E_{dc}}$ is applied across the plasma filament by placing two copper plane electrodes, plasma electrons start moving under the influence of the field. The charge is accumulated at the edge of filament and electric field is completely screened in the plasma. However, there is a transient process of redistribution of charges, and the temporal behavior of the electric current depends on relation between three parameters: the duration of the ionization process t ion, the electron collision time t col and the period of plasma oscillations. For typical laser pulse duration of 50 fs, the electron plasma density will be ~1016 cm−3 in a filament of radii 30–50 µm. Then, plasma period is approximately 1 ps, the collision time is ~100 ps; both of them longer than ionization time. Therefore one can consider the response of plasma with an instantaneous ionization, and the electric current which is directed along the direction of the external electric field (Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008).
Beating picosecond CO2 lasers are launched in the pre-existing plasma embedded with static field. Their pulse duration is greater than plasma period (~1 ps) so use of monochromatic wave approximation is justified in the present scheme. Lasers beat together in presence of static electric field and exert a ponderomotive force F p on plasma electrons given by
where ![]() ${{\vec F}_{\,pq}}$ is static ponderomotive force, given by
${{\vec F}_{\,pq}}$ is static ponderomotive force, given by
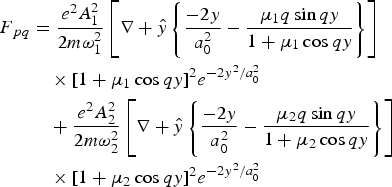 $$\eqalign{{F_{\,pq}} &= \displaystyle{{{e^2}A_1^2 } \over {2m{\rm \omega} _1^2 }}\left[{\nabla + \hat y\left\{{\displaystyle{{ - 2y} \over {a_0^2 }} - \displaystyle{{{{\rm \mu} _1}q\sin qy} \over {1 + {{\rm \mu} _1}\cos qy}}} \right\}} \right]\cr &\quad \times{\left[{1 + {{\rm \mu} _1}\cos qy} \right]^2}{e^{ - 2{y^2}/a_0^2 }} \cr & \quad + \displaystyle{{{e^2}A_2^2 } \over {2m{\rm \omega} _2^2 }}\left[{\nabla + \hat y\left\{{\displaystyle{{ - 2y} \over {a_0^2 }} - \displaystyle{{{{\rm \mu} _2}q\sin qy} \over {1 + {{\rm \mu} _2}\cos qy}}} \right\}} \right]\cr &\quad\times{\left[{1 + {{\rm \mu} _2}\cos qy} \right]^2}{e^{ - 2{y^2}/a_0^2 }}}$$
$$\eqalign{{F_{\,pq}} &= \displaystyle{{{e^2}A_1^2 } \over {2m{\rm \omega} _1^2 }}\left[{\nabla + \hat y\left\{{\displaystyle{{ - 2y} \over {a_0^2 }} - \displaystyle{{{{\rm \mu} _1}q\sin qy} \over {1 + {{\rm \mu} _1}\cos qy}}} \right\}} \right]\cr &\quad \times{\left[{1 + {{\rm \mu} _1}\cos qy} \right]^2}{e^{ - 2{y^2}/a_0^2 }} \cr & \quad + \displaystyle{{{e^2}A_2^2 } \over {2m{\rm \omega} _2^2 }}\left[{\nabla + \hat y\left\{{\displaystyle{{ - 2y} \over {a_0^2 }} - \displaystyle{{{{\rm \mu} _2}q\sin qy} \over {1 + {{\rm \mu} _2}\cos qy}}} \right\}} \right]\cr &\quad\times{\left[{1 + {{\rm \mu} _2}\cos qy} \right]^2}{e^{ - 2{y^2}/a_0^2 }}}$$By substituting cos qy = (e iqy + e −iqy) / 2 and sin qy = (e iqy + e −iqy)/2i, Eq. (4a) can be simplified to give an expression having two term e iqy and e −iqy. Out of these two, term having e iqy is responsible for exciting THz radiation at resonance condition. Term having e −iqy will be off resonant and can be neglected.
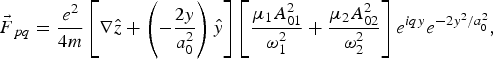 $${{\vec F}_{\,pq}} = \displaystyle{{{e^2}} \over {4m}}\left[{\nabla \hat z + \left({ - \displaystyle{{2y} \over {a_0^2 }}} \right)\hat y} \right]\left[{\displaystyle{{{{\rm \mu} _1}A_{01}^2 } \over {{\rm \omega} _1^2 }} + \displaystyle{{{{\rm \mu} _2}A_{02}^2 } \over {{\rm \omega} _2^2 }}} \right]{e^{iqy}}{e^{ - 2{y^2}/a_0^2 }}\comma \;$$
$${{\vec F}_{\,pq}} = \displaystyle{{{e^2}} \over {4m}}\left[{\nabla \hat z + \left({ - \displaystyle{{2y} \over {a_0^2 }}} \right)\hat y} \right]\left[{\displaystyle{{{{\rm \mu} _1}A_{01}^2 } \over {{\rm \omega} _1^2 }} + \displaystyle{{{{\rm \mu} _2}A_{02}^2 } \over {{\rm \omega} _2^2 }}} \right]{e^{iqy}}{e^{ - 2{y^2}/a_0^2 }}\comma \;$$![]() ${{\vec F}_{\,p{\rm \omega} }}$ is beat frequency ponderomotive force at frequency ω = ω1 − ω2, given by
${{\vec F}_{\,p{\rm \omega} }}$ is beat frequency ponderomotive force at frequency ω = ω1 − ω2, given by
 $${{\vec F}_{\,p{\rm \omega} }} = \displaystyle{{{e^2}} \over {2m{{\rm \omega} _1}{{\rm \omega} _2}}}\left[{\vec \nabla + \hat y\left\{{\displaystyle{{4y} \over {a_0^2 }} + q\left({\displaystyle{{{{\rm \mu} _1} + {{\rm \mu} _2}} \over 2}} \right){e^{iqy}}} \right\}} \right]{\vec E_1} \cdot \vec E_2^{\ast}.$$
$${{\vec F}_{\,p{\rm \omega} }} = \displaystyle{{{e^2}} \over {2m{{\rm \omega} _1}{{\rm \omega} _2}}}\left[{\vec \nabla + \hat y\left\{{\displaystyle{{4y} \over {a_0^2 }} + q\left({\displaystyle{{{{\rm \mu} _1} + {{\rm \mu} _2}} \over 2}} \right){e^{iqy}}} \right\}} \right]{\vec E_1} \cdot \vec E_2^{\ast}.$$
The static ponderomotive force causes ambipolar diffusion of plasma along ![]() $\hat y$. In the present study, time scale of diffusion is ~12 ps at 5 eV electron plasma temperature, which is much larger than the pulse duration (Malik et al., Reference Malik and Malik2013). In the steady state, the static ponderomotive force is balanced by the pressure gradient force giving rise to zero frequency transverse density ripple (Bhasin et al., Reference Bhasin and Tripathi2011),
$\hat y$. In the present study, time scale of diffusion is ~12 ps at 5 eV electron plasma temperature, which is much larger than the pulse duration (Malik et al., Reference Malik and Malik2013). In the steady state, the static ponderomotive force is balanced by the pressure gradient force giving rise to zero frequency transverse density ripple (Bhasin et al., Reference Bhasin and Tripathi2011),
 $${n_{0q}} = \displaystyle{1 \over 2}\displaystyle{{n_0^0 } \over {{T_e}}}\displaystyle{{{e^2}} \over {4m}}\left[{\displaystyle{{{{\rm \mu} _1}A_{01}^2 } \over {{\rm \omega} _1^2 }} + \displaystyle{{{{\rm \mu} _2}A_{02}^2 } \over {{\rm \omega} _2^2 }}} \right]{e^{iqy}}{e^{ - 2{y^2}/a_0^2 }}\comma \;$$
$${n_{0q}} = \displaystyle{1 \over 2}\displaystyle{{n_0^0 } \over {{T_e}}}\displaystyle{{{e^2}} \over {4m}}\left[{\displaystyle{{{{\rm \mu} _1}A_{01}^2 } \over {{\rm \omega} _1^2 }} + \displaystyle{{{{\rm \mu} _2}A_{02}^2 } \over {{\rm \omega} _2^2 }}} \right]{e^{iqy}}{e^{ - 2{y^2}/a_0^2 }}\comma \;$$
where T e is the equilibrium electron temperature. The beat frequency ponderomotive force imparts nonlinear oscillatory velocity ![]() $\vec {\rm \nu}_{\rm \omega}^{\,NL}$ to plasma electrons, which is evaluated by using the equation of motion. The nonlinear velocity at frequency ω = ω1 − ω2 has following two components at wave number
$\vec {\rm \nu}_{\rm \omega}^{\,NL}$ to plasma electrons, which is evaluated by using the equation of motion. The nonlinear velocity at frequency ω = ω1 − ω2 has following two components at wave number ![]() $\vec k = {\vec k_1} - {\vec k_2}$ and
$\vec k = {\vec k_1} - {\vec k_2}$ and ![]() $\vec k + q$
$\vec k + q$
The density perturbations ![]() $\vec n_{{\rm \omega} \comma \vec k}^{\,NL} \, \, {\rm and}\, \, \vec n_{{\rm \omega} \comma \vec k\_\vec q}^{\,NL} $ caused by the velocity perturbation (given by Eqs. (7)–(8)) are calculated by solving continuity equation
$\vec n_{{\rm \omega} \comma \vec k}^{\,NL} \, \, {\rm and}\, \, \vec n_{{\rm \omega} \comma \vec k\_\vec q}^{\,NL} $ caused by the velocity perturbation (given by Eqs. (7)–(8)) are calculated by solving continuity equation
 $$\eqalign{ \vec n_{{\rm \omega} \comma \vec k + \vec q}^{\,\,NL} & = \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar {k^2}} \over {4{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy\rpar }} \cr & \quad + \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar 2{q^2}} \over {4{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy\rpar }} \cr & \quad + \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar } \over {4{m^2}{\omega} {{ \omega} _1}{{\omega} _2}}}\displaystyle{{8qy} \over {a_0^2 }}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy - {\rm \pi} /2\rpar }}}.$$
$$\eqalign{ \vec n_{{\rm \omega} \comma \vec k + \vec q}^{\,\,NL} & = \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar {k^2}} \over {4{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy\rpar }} \cr & \quad + \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar 2{q^2}} \over {4{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy\rpar }} \cr & \quad + \displaystyle{{{e^2}{A_{01}}A_{02}^{\ast} \lpar {{\mu} _1} + {{\mu} _2}\rpar } \over {4{m^2}{\omega} {{ \omega} _1}{{\omega} _2}}}\displaystyle{{8qy} \over {a_0^2 }}{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz - qy - {\rm \pi} /2\rpar }}}.$$
Eqs. (7)–(8) can be easily reduced to expression obtained by Bhasin et al. (Reference Bhasin and Tripathi2011) by assuming planer wave front in place of Gaussian profiles of beating lasers. Following Bhasin et al. (Reference Bhasin and Tripathi2011), one may write the nonlinear current density at (![]() ${\rm \omega} \comma \; \vec k$) as:
${\rm \omega} \comma \; \vec k$) as:
 $$\eqalign{& \vec J_{{\rm \omega} \comma \vec k}^{\,NL} = {{\vec J}_1} + {{\vec J}_2} + {{\vec J}_3} \cr & \vec J_{{\rm \omega} \comma \vec k}^{\,NL} = - n_0^0 e\vec {\rm \nu}_{{\rm \omega} \comma \vec k}^{\,NL} - \vec n_{{\rm \omega} \comma \vec k}^{\,NL} e{{\vec {\rm \nu}}_{dc}} - n_{0q}^{\ast} e\vec {\rm \nu}_{{\rm \omega} \comma \vec k + \vec q}^{\,NL} }$$
$$\eqalign{& \vec J_{{\rm \omega} \comma \vec k}^{\,NL} = {{\vec J}_1} + {{\vec J}_2} + {{\vec J}_3} \cr & \vec J_{{\rm \omega} \comma \vec k}^{\,NL} = - n_0^0 e\vec {\rm \nu}_{{\rm \omega} \comma \vec k}^{\,NL} - \vec n_{{\rm \omega} \comma \vec k}^{\,NL} e{{\vec {\rm \nu}}_{dc}} - n_{0q}^{\ast} e\vec {\rm \nu}_{{\rm \omega} \comma \vec k + \vec q}^{\,NL} }$$
Here, the first term arises due to the coupling between equilibrium plasma densities n 00 and nonlinear velocity ![]() $\vec {\rm \nu}_{{\rm \omega} \comma \vec k}^{\,NL}$, the second term is due to nonlinear coupling between nonlinear density perturbation
$\vec {\rm \nu}_{{\rm \omega} \comma \vec k}^{\,NL}$, the second term is due to nonlinear coupling between nonlinear density perturbation ![]() $\vec n_{{\rm \omega} \comma \vec k}^{\,NL} $ and dc electron velocity
$\vec n_{{\rm \omega} \comma \vec k}^{\,NL} $ and dc electron velocity ![]() ${\vec {\rm \nu}_{dc}}$, and the third term is the result of coupling between zero frequency transverse density ripple n 0q* and nonlinear velocity
${\vec {\rm \nu}_{dc}}$, and the third term is the result of coupling between zero frequency transverse density ripple n 0q* and nonlinear velocity ![]() $\vec {\rm \nu}_{{\rm \omega} \comma \vec k + \vec q}^{\,NL}$. The dc electric field changes the THz radiation generation scenario due to the coupling between nonlinear density perturbation
$\vec {\rm \nu}_{{\rm \omega} \comma \vec k + \vec q}^{\,NL}$. The dc electric field changes the THz radiation generation scenario due to the coupling between nonlinear density perturbation ![]() $\vec n_{{\rm \omega} \comma \vec k}^{NL}$ and large dc velocity of plasma electrons in presence of dc electric field (Loffler et al., Reference Loffler, Jacbo and Roskos2000; Bhasin et al., Reference Bhasin and Tripathi2011). Due to large electron collision time period ~100 ps, plasma electron achieves large drift velocity (v dc = −eE dc/mυe) in presence of applied dc electric field. As a result of which nonlinear current contribution due to J 2 becomes significant as compared to J 3 (for lower values of pump intensities), as shown in Figure 2. Resolving Eq. (11) into y and z components, we obtain
$\vec n_{{\rm \omega} \comma \vec k}^{NL}$ and large dc velocity of plasma electrons in presence of dc electric field (Loffler et al., Reference Loffler, Jacbo and Roskos2000; Bhasin et al., Reference Bhasin and Tripathi2011). Due to large electron collision time period ~100 ps, plasma electron achieves large drift velocity (v dc = −eE dc/mυe) in presence of applied dc electric field. As a result of which nonlinear current contribution due to J 2 becomes significant as compared to J 3 (for lower values of pump intensities), as shown in Figure 2. Resolving Eq. (11) into y and z components, we obtain
 $$\eqalign{& J_{y{\rm \omega} \comma k}^{NL} = \displaystyle{{n_0^0 {e^4}A_{01}^{} A_{02}^{\ast} } \over {2{m^3}{ \omega} {{ \omega} _1}{{ \omega} _2}}} \cr & \quad \left[{\displaystyle{{{k^2}{E_{dc}}} \over {{{\rm \nu} _e}{\rm \omega} }} - \displaystyle{{eq\lpar {{ \mu} _1} + {{\mu} _2}\rpar } \over {8{T_e}}}\left\{{\displaystyle{{{{\mu} _1}A_{01}^2 } \over {{\omega} _1^2 }} + \displaystyle{{{{\mu} _2}A_{02}^2 } \over {{\omega} _2^2 }}} \right\}{e^{ - 2{y^2}/a_0^2 }}} \right]{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz\rpar }}\comma \; }$$
$$\eqalign{& J_{y{\rm \omega} \comma k}^{NL} = \displaystyle{{n_0^0 {e^4}A_{01}^{} A_{02}^{\ast} } \over {2{m^3}{ \omega} {{ \omega} _1}{{ \omega} _2}}} \cr & \quad \left[{\displaystyle{{{k^2}{E_{dc}}} \over {{{\rm \nu} _e}{\rm \omega} }} - \displaystyle{{eq\lpar {{ \mu} _1} + {{\mu} _2}\rpar } \over {8{T_e}}}\left\{{\displaystyle{{{{\mu} _1}A_{01}^2 } \over {{\omega} _1^2 }} + \displaystyle{{{{\mu} _2}A_{02}^2 } \over {{\omega} _2^2 }}} \right\}{e^{ - 2{y^2}/a_0^2 }}} \right]{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz\rpar }}\comma \; }$$ $$\eqalign{&J_{z{\rm \omega} \comma k}^{NL} = - \displaystyle{{n_0^0 {e^3}A_{01}^{} A_{02}^{\ast} k} \over {2{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}\cr & \quad \left[{1 + \displaystyle{{{e^2}\lpar {{\mu} _1} + {{\mu} _2}\rpar } \over {16m{T_e}}}\left\{{\displaystyle{{{{\mu} _1}A_{01}^2 } \over {{\omega} _1^2 }} + \displaystyle{{{{\mu} _2}A_{02}^2 } \over {{\omega} _2^2 }}} \right\}{e^{ - 2{y^2}/a_0^2 }}} \right]{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz\rpar }}.}$$
$$\eqalign{&J_{z{\rm \omega} \comma k}^{NL} = - \displaystyle{{n_0^0 {e^3}A_{01}^{} A_{02}^{\ast} k} \over {2{m^2}{\omega} {{\omega} _1}{{\omega} _2}}}\cr & \quad \left[{1 + \displaystyle{{{e^2}\lpar {{\mu} _1} + {{\mu} _2}\rpar } \over {16m{T_e}}}\left\{{\displaystyle{{{{\mu} _1}A_{01}^2 } \over {{\omega} _1^2 }} + \displaystyle{{{{\mu} _2}A_{02}^2 } \over {{\omega} _2^2 }}} \right\}{e^{ - 2{y^2}/a_0^2 }}} \right]{e^{ - 2{y^2}/a_0^2 }}{e^{ - i\lpar {\rm \omega} t - kz\rpar }}.}$$
It can be observed from Eq. (12) that J NL varies as ~e −i(ωt-kz), where ![]() $\vec k = {\vec k_1} - {\vec k_2} + \vec q$, and it is responsible for THz radiation generation. It is clear that wave number q of electrostatic density ripples is responsible for providing extra momentum to achieve resonance condition. The periodic nature of transverse density ripples is must, otherwise,
$\vec k = {\vec k_1} - {\vec k_2} + \vec q$, and it is responsible for THz radiation generation. It is clear that wave number q of electrostatic density ripples is responsible for providing extra momentum to achieve resonance condition. The periodic nature of transverse density ripples is must, otherwise, ![]() $\vec k\lpar \!= {\vec k_1} - {\vec k_2} + \vec q\rpar $ will exhibit non-periodic behavior; resonance condition cannot be achieved and maximum energy transfer will not take place and consequently a weak field THz radiation will be generated (Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013). The transverse y-component of wave equation governing the propagation of THz wave can be written as
$\vec k\lpar \!= {\vec k_1} - {\vec k_2} + \vec q\rpar $ will exhibit non-periodic behavior; resonance condition cannot be achieved and maximum energy transfer will not take place and consequently a weak field THz radiation will be generated (Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013). The transverse y-component of wave equation governing the propagation of THz wave can be written as
 $$\displaystyle{{{\partial ^2}{E_y}} \over {\partial {z^2}}} + \left({\displaystyle{{{{\rm \omega} ^2}{\rm \varepsilon} } \over {{c^2}}}} \right){E_y} = \displaystyle{{ - 4{\rm \pi} i{\rm \omega} } \over {{c^2}}}\vec J_y^{NL}\comma \;$$
$$\displaystyle{{{\partial ^2}{E_y}} \over {\partial {z^2}}} + \left({\displaystyle{{{{\rm \omega} ^2}{\rm \varepsilon} } \over {{c^2}}}} \right){E_y} = \displaystyle{{ - 4{\rm \pi} i{\rm \omega} } \over {{c^2}}}\vec J_y^{NL}\comma \;$$
where, ε(ω) = 1 − ωp2 / ω2 is the plasma permittivity at the THz frequency and ωp2 = 4πn 00e 2 / m. The dispersion relation of THz wave is given by k 2 = (ω2/c 2)(1 − ωp2/ω2) which is obtained by placing the right-hand side of Eq. (13) (i.e., source term) equal to zero. This mode can freely propagate through the plasma if ω > ωp. This can also be observed from the plot between normalized propagation vector (kc/ωp) and normalized frequency (ω/ωp) of THz radiation in Figure 3. To plot this figure, we have utilized resonance conditions ω = ω1 − ω2 and ![]() $\vec k = {\vec k_1} - {\vec k_2} + \vec q$. In this study, ω/ωp = 2.5 − 5 (corresponding to 8 THz to 30 THz), which satisfy the above said condition (ω > ωp). Thus, this mode can easily propagate through the plasma. Field profiles of co-propagating lasers given by Eq. (1) also satisfy the dispersion relation k 2 = (ω2/c 2)(1 − ωp2/ω2). For the present set of parameters plasma frequency f p ≈ 100 v p, where v p is the collision frequency. Thus, use of collisionless plasma dispersion relation is justified. Eq. (13) can be solved over the length L of the plasma column and the normalized THz amplitude can be written as follows:
$\vec k = {\vec k_1} - {\vec k_2} + \vec q$. In this study, ω/ωp = 2.5 − 5 (corresponding to 8 THz to 30 THz), which satisfy the above said condition (ω > ωp). Thus, this mode can easily propagate through the plasma. Field profiles of co-propagating lasers given by Eq. (1) also satisfy the dispersion relation k 2 = (ω2/c 2)(1 − ωp2/ω2). For the present set of parameters plasma frequency f p ≈ 100 v p, where v p is the collision frequency. Thus, use of collisionless plasma dispersion relation is justified. Eq. (13) can be solved over the length L of the plasma column and the normalized THz amplitude can be written as follows:
 $$\eqalign{& {A_y} = \left\vert {\displaystyle{{{E_y}} \over {{A_{01}}}}} \right\vert \approx \displaystyle{{{\rm \nu}_{02}^{\prime} {q^{\prime}}} \over {16}}\left[{{{\mu} _1}v_{01}^{^{\prime}2} + {{\mu} _2}v_{02}^{^{\prime}2} } \right]\cr & \quad \displaystyle{{{{\mu} _1} + {{\mu} _2}} \over {\sqrt {\rm \varepsilon} \lpar \sqrt {\rm \varepsilon} - 1\rpar { \omega} _1^{\prime} {k^{^{\prime}2}}}}{e^{ - 2{{{y^2}} / {a_0^2 }}}} + \displaystyle{{{\rm \nu}_{02}^{\prime} v_{dc}^{\prime} } \over {2{\omega} _1^{\prime} {\omega} _{}^{\prime} \sqrt {\rm \varepsilon} \lpar \sqrt {\rm \varepsilon} - 1\rpar }}{e^{ - 2{{{y^2}} / {a_0^2 }}}}}$$
$$\eqalign{& {A_y} = \left\vert {\displaystyle{{{E_y}} \over {{A_{01}}}}} \right\vert \approx \displaystyle{{{\rm \nu}_{02}^{\prime} {q^{\prime}}} \over {16}}\left[{{{\mu} _1}v_{01}^{^{\prime}2} + {{\mu} _2}v_{02}^{^{\prime}2} } \right]\cr & \quad \displaystyle{{{{\mu} _1} + {{\mu} _2}} \over {\sqrt {\rm \varepsilon} \lpar \sqrt {\rm \varepsilon} - 1\rpar { \omega} _1^{\prime} {k^{^{\prime}2}}}}{e^{ - 2{{{y^2}} / {a_0^2 }}}} + \displaystyle{{{\rm \nu}_{02}^{\prime} v_{dc}^{\prime} } \over {2{\omega} _1^{\prime} {\omega} _{}^{\prime} \sqrt {\rm \varepsilon} \lpar \sqrt {\rm \varepsilon} - 1\rpar }}{e^{ - 2{{{y^2}} / {a_0^2 }}}}}$$
where ν01′ = eA 01 / mω1c, ν02′ = eA 02 / mω2c, νdc′ = eE dc / mνec, q ′ = qc / ωp, k ′ = kνth / ωp, ω1′ = ω1 / ωp, and ω2′ = ω2 / ωp. Eq. (14) does not depend on the plasma length because we are concerned only with stationary solutions for THz radiation generation. The THz radiation can easily propagate out of the plasma because damping for THz electromagnetic wave is negligible for the parameters of present scheme and even plasma length can be adjusted in experimental set-ups according to the skin depth of plasma. One can notice that normalized THz amplitude is directly proportional to laser power, but dc electric field term (second term) is very small as compared to beat wave ponderomotive force term (first term) at high filament intensities in Eq. (14). To check the contribution of the two terms on the right-hand side of Eq. (14), we plot the variation of normalized amplitude of THz wave with respect to normalized oscillatory velocities ![]() ${\rm \nu}_{01}^{\prime} \!\sim \!v_{02}^{\prime} $ of beating laser in Figure 4. In the present work, there are two types of ponderomotive forces due to lasers envelop: (1) Static ponderomotive force
${\rm \nu}_{01}^{\prime} \!\sim \!v_{02}^{\prime} $ of beating laser in Figure 4. In the present work, there are two types of ponderomotive forces due to lasers envelop: (1) Static ponderomotive force ![]() ${\vec F_{\,pq}}$ which does not contribute directly in exciting THz generation, but forms transverse density ripples by balancing the pressure gradient force. These density ripples provides necessary mismatch in
${\vec F_{\,pq}}$ which does not contribute directly in exciting THz generation, but forms transverse density ripples by balancing the pressure gradient force. These density ripples provides necessary mismatch in ![]() $\vec k$ values at resonance. (2) Beat frequency ponderomotive force
$\vec k$ values at resonance. (2) Beat frequency ponderomotive force ![]() ${\vec F_{\,p{\rm \omega} }}$ at frequency ω = ω1 − ω2.
${\vec F_{\,p{\rm \omega} }}$ at frequency ω = ω1 − ω2. ![]() ${\vec F_{\,p{\rm \omega} }}$ is directly responsible for enhancing the amplitude of THz radiation.
${\vec F_{\,p{\rm \omega} }}$ is directly responsible for enhancing the amplitude of THz radiation.

Fig. 2. (Color online) Plot of normalized current density J yNL / n 00ec as a function of normalized electron velocity ν01′. Other parameters are q ′=0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′ = 50, νdc′ = 0.053, ω′ = 3 and y/a 0 = 0.1.

Fig. 3. (Color online) Plot of dispersion relation of THz radiation.

Fig. 4. (Color online) Plot of normalized THz amplitude as a function of normalized electron velocity ν01′ ~ ν02′ by (i) considering only first term of Eq. (14) on right-hand side (dashed line), (ii) considering only second term of Eq. (14) on right-hand side (dotted line), and (iii) considering both terms of Eq. (14) on RHS (solid line). Other parameters are q ′ = 0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′ = 50, νdc′ = 0.053, ω′ = 3 and y/a 0 = 0.1.
Another force responsible for enhancing the amplitude of THz radiation is electric force due to applied dc electric field ![]() ${\vec E_{dc}}$. Thus
${\vec E_{dc}}$. Thus ![]() ${\vec F_{\,p{\rm \omega} }}$ and
${\vec F_{\,p{\rm \omega} }}$ and ![]() $ - e{\vec E_{dc}}$ forces on plasma electrons contribute directly to THz amplitude. First and second term on the right-hand side of Eq. (14) represent contribution of
$ - e{\vec E_{dc}}$ forces on plasma electrons contribute directly to THz amplitude. First and second term on the right-hand side of Eq. (14) represent contribution of ![]() ${\vec F_{\,p{\rm \omega} }}$ and
${\vec F_{\,p{\rm \omega} }}$ and ![]() $- e{\vec E_{dc}}$ forces to the amplitude A y of the THz radiation, respectively. Their relative contributions are observed by plotting both the terms as a function of ν01′ (~ν02′) in Figure 4. Up to ν01′ ≅ 0.16 electric force contribution is more effective
$- e{\vec E_{dc}}$ forces to the amplitude A y of the THz radiation, respectively. Their relative contributions are observed by plotting both the terms as a function of ν01′ (~ν02′) in Figure 4. Up to ν01′ ≅ 0.16 electric force contribution is more effective ![]() $\lpar \vert - e{\vec E_{dc}}\vert \gt {\vec F_{\,p{\rm \omega} }}\rpar $, while after ν01′ > 0.16 contribution of
$\lpar \vert - e{\vec E_{dc}}\vert \gt {\vec F_{\,p{\rm \omega} }}\rpar $, while after ν01′ > 0.16 contribution of ![]() ${{\mathop{F} \limits^{\leftarrow}}_{p{\rm \omega} }}$ becomes more significant than
${{\mathop{F} \limits^{\leftarrow}}_{p{\rm \omega} }}$ becomes more significant than ![]() $ - e{\vec E_{dc}}$ force
$ - e{\vec E_{dc}}$ force ![]() $\lpar {\vec F_{\,p{\rm \omega} }} \gt \vert - e{\vec E_{dc}}\vert \rpar $. Intensities of beating lasers [I = (1.384 × 1018)(a 02 / λ2), here I is in W/cm2, λ in micron] come out to be ~ 1014 W/cm2 corresponding to ν01′≈ν01′≈0.16. λ = 10 µm are chosen corresponding to picosecond CO2 laser. Thus, effects of dc electric field can be utilized only at low filament intensities (~1014 W/cm2) of beating lasers. Eq. (14) reveals that the normalized THz amplitude is proportional to square of filament cross-section (μ12, μ22 and μ1μ2), thus, THz field increases on increasing μ1 and μ2. Its explanation lies in Eqs. (6) and (12); higher the value of μ1 and μ2, greater the amplitude of density ripples n q0 (Eq. (6)) which means, higher number of electrons will be involved in the generation of oscillatory nonlinear current
$\lpar {\vec F_{\,p{\rm \omega} }} \gt \vert - e{\vec E_{dc}}\vert \rpar $. Intensities of beating lasers [I = (1.384 × 1018)(a 02 / λ2), here I is in W/cm2, λ in micron] come out to be ~ 1014 W/cm2 corresponding to ν01′≈ν01′≈0.16. λ = 10 µm are chosen corresponding to picosecond CO2 laser. Thus, effects of dc electric field can be utilized only at low filament intensities (~1014 W/cm2) of beating lasers. Eq. (14) reveals that the normalized THz amplitude is proportional to square of filament cross-section (μ12, μ22 and μ1μ2), thus, THz field increases on increasing μ1 and μ2. Its explanation lies in Eqs. (6) and (12); higher the value of μ1 and μ2, greater the amplitude of density ripples n q0 (Eq. (6)) which means, higher number of electrons will be involved in the generation of oscillatory nonlinear current ![]() $\vec J_{{\rm \omega} \comma k}^{NL} $ (Eq. (12)). Higher number of charge carriers result into higher nonlinear current which leads to more efficient THz radiation. In Figure 5, variation of normalized THz amplitude is shown as a function of THz frequency (v) and beam width parameter (y/a 0) at ν01′ ~ ν02′ ~ 0.005. THz amplitude increases with THz frequency. The increase in THz amplitude can be attributed to the change in plasma permittivity ε(ω) = 1 − ωp2 / ω2 as a function of THz frequency (ω). The factor
$\vec J_{{\rm \omega} \comma k}^{NL} $ (Eq. (12)). Higher number of charge carriers result into higher nonlinear current which leads to more efficient THz radiation. In Figure 5, variation of normalized THz amplitude is shown as a function of THz frequency (v) and beam width parameter (y/a 0) at ν01′ ~ ν02′ ~ 0.005. THz amplitude increases with THz frequency. The increase in THz amplitude can be attributed to the change in plasma permittivity ε(ω) = 1 − ωp2 / ω2 as a function of THz frequency (ω). The factor ![]() $\lpar \sqrt {\rm \varepsilon} - 1\rpar $ appearing in the denominator of Eq. (14) decreases 2.5 times as ω/ωp changes from 2.5 to 5, which results into approximately two-fold increases in THz amplitude. THz amplitude is maximum at axis (y/a 0 = 0) and decreases as one moves off axis. In Figure 6, we plot normalized THz amplitude as a function dc electric field E dc(KV/cm) and beam width parameter (y/a 0) for following set of parameters: q ′ = 0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′= 50, ω′ = 3 and y/a 0 = 0.1. It is observed that as one increases E dc, normalized THz amplitude increases continuously at normalized velocity ν01′ ~ ν02′ ~ 0.005. THz amplitude is nearly two times higher as compared to the scheme suggested by Bhasin et al. (Reference Bhasin and Tripathi2011), for the same set of parameters. Effects of finite laser spot size are not included in the present scheme because the maximum off axis distance utilized in the present scheme is up to y/a 0 = 1. In the present scheme plasma is considered unmagnetized where polarization field effect are not significant (Chen et al., Reference Chen1983).
$\lpar \sqrt {\rm \varepsilon} - 1\rpar $ appearing in the denominator of Eq. (14) decreases 2.5 times as ω/ωp changes from 2.5 to 5, which results into approximately two-fold increases in THz amplitude. THz amplitude is maximum at axis (y/a 0 = 0) and decreases as one moves off axis. In Figure 6, we plot normalized THz amplitude as a function dc electric field E dc(KV/cm) and beam width parameter (y/a 0) for following set of parameters: q ′ = 0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′= 50, ω′ = 3 and y/a 0 = 0.1. It is observed that as one increases E dc, normalized THz amplitude increases continuously at normalized velocity ν01′ ~ ν02′ ~ 0.005. THz amplitude is nearly two times higher as compared to the scheme suggested by Bhasin et al. (Reference Bhasin and Tripathi2011), for the same set of parameters. Effects of finite laser spot size are not included in the present scheme because the maximum off axis distance utilized in the present scheme is up to y/a 0 = 1. In the present scheme plasma is considered unmagnetized where polarization field effect are not significant (Chen et al., Reference Chen1983).

Fig. 5. (Color online) Variation of normalized THz amplitude as a function of THz frequency υ and normalized beam width parameter y/a 0. Other parameters are q ′ = 0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′ = 50, νdc′ = 0.053 and ν01′ ~ ν02′ ~ 0.005.

Fig. 6. (Color online) Plot of normalized THz amplitude as a function of dc electric field E dc and normalized beam width parameter y/a 0. Other parameters are q ′ = 0.3, k ′ ≈ 0.01, μ1 ~ μ1 ~ 0.3, ω1′ = 50, ω′ = 3 and ν01′ ~ ν02′ ~ 0.005.
3. CONCLUSIONS
We have studied the dynamics of generation of THz wave by the beating of two laser beams in the presence of static electric field, when only ponderomotive nonlinearity is operative. Gaussian envelop of filamented laser beams is considered in the scheme. The nonlinear mechanism which generates the THz radiation can be understood as follows: the nonlinear interaction of the laser beams with the plasma having static magnetic field generates the velocity perturbation which leads to density perturbation in the electron density. Static electric field also imparts dc velocity to electrons. Two components of ponderomotive force (Eqs. (4) and (5)) are responsible for density perturbation. As a result, a nonlinear current at beat wave frequency is generated due to the coupling between various density and velocity components of electrons as shown in Eq. (12). Since the difference in laser beam frequencies is in the range of THz and phase matching conditions are satisfied, the nonlinear current generated at beat frequency generates the desired THz wave. The THz amplitude can be controlled by laser-plasma parameters and magnitude of static electric field as shown in Eq. (14). Taking into account the Gaussian envelop, the growth of THz radiation amplitude is increased almost 10 times when the magnitude of normalized oscillatory velocities is increased from 0.005 to 0.01 in comparison to plane laser beams suggested by Bhasin et al. (Reference Bhasin and Tripathi2011). THz amplitude also increases significantly with the beat wave frequency. Our numerical results also show that amplitude of THz is high at small y/a 0, which shows that laser plasma interaction in paraxial region may play an important role to enhance the amplitude of THz. All these results can be useful in developing THz pulsed imaging as a medical imaging tool because the THz amplitude can be easily tuned by changing applied dc electric field upto the intensity level of ~ 1014 W/cm2. The THz frequencies correspond to energy levels of molecular rotations and vibrations of DNA (Markelz et al., Reference Markelz, Roitberg and Heilwiel2000) and proteins (Walther et al., Reference Walther, Fischer and Schall2000), which may provide characteristic fingerprints to differentiate biological tissues in a region of the spectrum not previously explored for medical use. THz wavelengths are particularly sensitive to water and exhibit absorption peaks due to stretching modes at 6 THz and vibrational modes at 19.5 THz. This makes the technique very sensitive to hydration state (Mittleman et al., Reference Mittleman, Jacobsen and Nuss1996) which can indicate tissue condition.








